Об эффекте занижения коэффициента линейной регрессии «шумами» данных, или почему все-таки «регрессия» / forpes.ru

Главная
Об эффекте занижения коэффициента линейной регрессии «шумами» данных, или почему все-таки «регрессия»

Об эффекте занижения коэффициента линейной регрессии «шумами» данных, или почему все-таки «регрессия» +6

28.02.2023 07:12

SanSanychSeva 31 1800 Источник

Введение

Как сказал Йозеф Швейк, войдя в одно очень уважаемое заведение, "Добрый вечер всей честной компании" - от себя мне осталось лишь присовокупить к этой блестящей фразе "пользователей контента Хабра!" Прошу, однако же, в отличие от истории Швейка, не встречать мое приветствие "тычками под ребра" и комментариями про идиотизм автора, решившегося представить свой первый опус взыскательной публике.

Речь пойдет о небольшом поучительном факте в области линейной регрессии, который будет показан экспериментально и объяснен аналитическими формулами на примере простой линейной регрессии. Этот факт, наверняка, известен тем, кто основательно изучал тему линейной регрессии регулярным образом, однако самоучки и выпускники интернет курсов, имя которым сегодня легион благодаря популярности темы, вполне могли проскочить мимо него.

Знание данного факта может оказаться практически полезно для коррекции интуитивных представлений о линейной регрессии - что и сподвигло автора на написание данной заметки после того, как он сам его обнаружил, выполняя упражнения к книге "An Introduction To Statistical Learning v2" авторов Gareth James, Daniela Witten, Trevor Hastie, Robert Tibshirani.

По-видимому, именно данный эффект исторически и привел к использованию термина "регрессия" - как известно, автор термина Фрэнсис Гальтон исследовал статистику роста в поколениях сыновей и отцов, и обнаружил, что линия определенно имеет наклон менее 45 градусов, из чего в его работе "Регрессия к посредственности при наследовании роста" был сделан вывод о вырождении индивидуальности роста человека в будущих поколениях к некому среднему значению роста.

Читатель, которому более близко познание мира через свой опыт, может прекратить дальнейшее чтение и самостоятельно обнаружить все написанное далее, проделав упражнения номер 11 и 12 к главе №3 "Linear Regression" книги "An Introduction To Statistical Learning v2" авторов Gareth James, Daniela Witten, Trevor Hastie, Robert Tibshirani, доступной для скачивания на сайте авторов.

Часть первая: Суть и теория эффекта

Психологическая преамбула

В простой линейной регрессии принято полагать связь между истинными случайными величинами X и Y описываемой формулой

$Y\ =\ \beta_0 + \beta_1\cdot X + \varepsilon ,$

где матожидание случайной величины $E(\varepsilon)=0$ . (И даже том случае, если истинная связь нелинейна, мы предполагаем возможность ее аппроксимации в каком-то диапазоне Х такой формулой, убирая нелинейные эффекты в $\varepsilon$ )

Имея конкретную выборку объектов $\{x_i,y_i\} \,\mbox{, где}\, i \in \{1,...n\}$ , мы строим модель простой линейной регрессии (далее SLR) по формуле

$y_i\, =\, \hat\beta_0 + \hat\beta_1\cdot x_i + \hat\epsilon_i$

Если выборка является примером из реальной жизни, то мы не знаем истинных $\beta_0$ и $\beta_1$ и "горды сознанием", взирая на результаты работы своей модели SLR: $\hat\beta_0$ и $\hat\beta_1$ , обозначенные знаком крышечки сверху. Более того, если мы самостоятельно генерим выборку для численного эксперимента, используя рандомные функции по той же логике:

сперва генерим выборку на основе какого-то распределения для ,
выбираем для сокращения дальнейших рассуждений, но без снижения общности выводов: $\beta_1 > 0$ ,
потом берем линейный член по и добавляем, например, стандартное нормальное распределение для члена с $\epsilon$ : $y_i = \beta_0 + \beta_1\cdot x_i + N(0,1)_i$ ,

то тренируя модель SLR на сгенеренной выборке (у которой мы уже знаем истинные коэффициенты $\beta_0$ и $\beta_1$ !) мы получим также, что ни при какой большой статистической мощности выборки нельзя отвергнуть нулевую гипотезу $H_0:\, \hat\beta_1 = \beta_1$ , что наполняет нас радостью от того, что статистическая наука не подкачала, ну и мы нигде не "налажали"!

Однако попытка интуитивно ответить на простой вопрос "каково будет ожидаемое значение коэффициента наклона регрессионной прямой при обратной линейной регрессии X на Y на той же самой выборке (то есть никакой новой генерации - только столбцы X и Y переименовали) необратимо поделит незнакомых с данным эффектом начинающих DA/DS-ов на два непересекающихся в одном измерении кластера:

на успешных в будущем бизнес консультантов, которые не моргнув глазом подгонят любые результаты под интуитивные желания бизнеса, за что будут обласканы мамоной,
и на честных ботаников, которые, нарушив требования гигиены труда к разумному чередованию работы и отдыха и разочаровав начальство переносами дедлайна, все же придут к неумолимому выводу, что для обратной регрессии наклон кривой будет статистически значимо отличаться от интуитивно ожидаемого значения $1/\beta_1$ .

Введя обозначения для коэффициентов обратной регрессии как

$x_i = \hat\beta_0^T + \hat\beta_1^T\cdot y_i + \hat\epsilon_i^T ,$

мы можем переписать неумолимый вывод честных ботаников как тот факт, что при достаточно большой выборке всегда можно статистически значимо утверждать, что верна альтернативная гипотеза $H_1:\, \hat\beta_1^T \ne 1/\beta_1$ - здесь индекс означает смену местами X и Y (аналог транспонирования).

Когнитивный диссонанс обманутой интуиции побуждает нас, честных ботаников, разобраться в чем причина.

Формулы

По счастью, в простой линейной регрессии аналитические формулы для коэффициентов получаются без матричных выражений, и даже (способный к математике) старшеклассник сможет их преобразовывать. Поэтому, не оскорбляя читателя сомнениями в его способностях, сразу приведем конечные выражения для связи $\hat\beta_1$ и $\hat\beta_1^T$ в симметричном относительно обмена X и Y виде:

$\left\{\begin{eqnarray}&\hat\beta_1\cdot\hat\beta_1^T &=& \hat R^2 \\&\hat\beta_1\cdot D(x_i) &=&\hat\beta_1^T\cdot D(y_i) \\\end{eqnarray}\right.$

где D - это квадратичная дисперсия соответствующей величины на выборке, а значение характерной метрики $\hat R^2$ равно для двумерного случая квадрату коррелятора на данной выборке. NB!: Причем, все это не асимптотические формулы при размере выборки, стремящемся к бесконечности, но абсолютно точные формулы, строго выполняющиеся для произвольной выборки любого размера.

Полные выкладки по получению данных формул из условия минимума квадратичной функции потерь можно найти, например, вот здесь: https://github.com/SanSanychSeva/Exercises-from-Introduction-to-Statistical-Learning-done-in-Python/blob/main/chapter_03_Linear_Regression/SLR formulas from ISLRv2.ipynb

Некоторые быстрые выводы из симметричности системы уравнений для коэффициентов наклонов кривых

Как видим, только при полной корреляции X и Y верно интуитивное ожидание, что $\hat\beta_1^T = 1/\hat\beta_1$ , иначе же имеем заниженное значение (при положительном $\beta_1$ - в общем случае следует говорить про "более горизонтальную" прямую регрессии).
Который именно из коэффициентов будет сильнее занижен относительно "истинных значений" $\beta_1$ и $1/\beta_1$ - это определяется балансом дисперсий обеих величин. Может быть занижен и только один из них - см. ниже в каком случае.
В частности, если дисперсии X и Y одинаковы, то $\hat\beta_1 = \hat\beta_1^T = <X,Y>$ , а так как коррелятор меньше 1, то имеем очевидное объяснение эффекта регрессии взрослого роста при сравнении статистик в разных поколениях. Забавно, но если бы сэр Фрэнсис Гальтон повторил свое исследование, поменяв или случайно перепутав в данных роста где у него отцы, а где дети, то эффект был бы одинаков в обе стороны по времени (при условии, что статистическая погрешность измерения роста в разные эпохи была одинакова).

Интерпретация и философские выводы

При генерации выборки объектов мы на самом деле заложили в логику генерации отсутствие стохастичности X - именно поэтому регулярная часть Y описывалась как $Y_{рег} = \beta_0 + \beta_1\cdot X$ . То есть мы рассматривали X как некоторую совокупность точных значений. Строго говоря этого никогда не бывает - в данных есть стохастические шумы, и нам следовало бы генерить данные по принципу:

$X = X_{рег} + St_x$ $Y = \beta_0 + \beta_1\cdot X_{рег} + St_y + \varepsilon_y$

где "Штос-член" определял бы стохастичность измерения истинного значения каждой переменной, а $\varepsilon_y$ агрегировал бы в себе усреднение зависимости истинных переменных по популяционному распределению неучитываемых других предикторов при регрессии Y на X. В этом случае уже при прямой регрессии Y на X у нас было бы видно, что статистически верна альтернативная гипотеза $H_1:\, \hat\beta_1 \ne \beta_1$ , что собственно и наблюдал автор термина "регрессия" в своем исследовании.

Объяснение эффекта "на пальцах"

Предположим, что никакой стохастизации нет, коррелятор <X,Y> = 1, то есть все точки выборки лежат на "истинной" прямой.
Возьмем теперь пару объектов выборки, которые лежат в небольшой окрестности точки - для конкретности, правее "центра масс" выборки $(\bar x,\bar y)$ . Пока данные объекты лежат на "истинной прямой", оба объекта "голосуют" за истинный наклон. Теперь смоделируем влияние стохастизации по разным осям на регрессию Y по X:

Если объекты раздвинуть по оси X в разные стороны на расстояние $\delta$ так, что теперь они "тянут" регрессионную прямую в разные стороны, то у них появится вращающий момент во влиянии на наклон регрессионной прямой (Y на X), приближающий ее в горизонтальному положению - так как у них теперь разные плечи по оси X: $x_0-\bar x - \delta$ и $x_0-\bar x + \delta$ .
Если объекты аналогично раздвинуть по оси Y, дополнительного вращающего момента во влиянии на наклон регрессионной (Y на X) прямой не возникнет - так как у них обоих плечи по оси X не поменялись, оставшись равными $x_0-\bar x$ .

Именно поэтому в стандартном численном эксперименте выше получаем невозможность опревергнуть нулевую гипотезу $H_0:\, \hat\beta_1 = \beta_1$ : стохастизация только Y при генерации выборки не горизонтирует регрессионную прямую для Y на X. А вот когда мы меняем местами X и Y, то в обратной регрессии горизонтальной осью становится бывший Y, в результате регрессионная прямая становится более горизонтальной, чем $1/\beta_1$

Замечание: кажется странным, что при регрессии Y на X речь идет только о плече вдоль оси X - поскольку интуитивно мы воспринимаем регрессионную прямую как рычаг с точкой опоры в "центре масс" $(\bar x,\bar y)$ , и рычагом должна служить не проекция на ось X, а проекция на сам рычаг. Но причина в том, что в линейной регрессии функцией потерь является не сумма квадратов расстояний до регрессионной прямой в пространстве $X\bigotimes Y$ , но сумма квадратов residual errors $y_i-\hat y_i$ , где крышечка над означает предсказанное на объекте значение: $\hat y_i = \hat\beta_0 + \hat\beta_1\cdot x_i$ .

Выводы

Но ведь у нас любые физические величины имеют погрешность измерения, а реальные данные - ненулевой уровень стохастического шума. Тогда все вышесказанное означает, что при линейной регрессии мы в принципе получаем всегда только оценку снизу для степени "истинной" зависимости Y(X), отраженной в любом эксперименте. Чем больше шума в предикторе, тем меньше физического смысла в результате линейной регрессии. Оценку сверху мы получаем проделав обратную регрессию и транспонировав обратно оси координат - то есть, например, при положительном $\beta_1$ имеем: $\hat\beta_1 \le \beta_1 \le 1/\hat\beta_1^T$ . Таким образом при обработке данных любого эксперимента мы получаем диапазон, внутри которого лежит "истинная" взаимосвязь двух физических величин.
Оставив в стороне Штос-член, рассмотрим стохастический член $\varepsilon$ . Как уже говорилось, по факту, в нем агрегировано влияние других предикторов при их свертке до двумерной зависимости между Y и X. При этом для регрессии Y на X мы проводим данную свертку при постоянных X, а для регрессии Х на Y мы проводим данную свертку при постоянных Y - получая в общем случае разные $\varepsilon_y$ и $\varepsilon_х$ . Но тогда для выбора более точной модели может оказаться принципиально заранее знать, что же все-таки причинно-следственно от чего зависит в реальной жизни - Y от X или X от Y.

Часть вторая: Численный эксперимент

Проведем эксперимент для простой иллюстрации теории выше - не будем загромождать статью строгими проверками гипотез вида $H_0:\, \hat\beta_1 = \beta_1$ . Если кто-то желает увидеть более строгий анализ с t-статистикой для $\hat\beta_k$ - можно посмотреть, например, здесь: https://github.com/SanSanychSeva/Exercises-from-Introduction-to-Statistical-Learning-done-in-Python/blob/main/chapter_03_Linear_Regression/exercise_11and12.ipynb).

Воспользуемся библиотеками Питон:

import math
import pandas as pd
import numpy as np
from sklearn import linear_model

Генерация первой выборки: стохастизация только по Y, разные дисперсии X и Y

возьмем $\beta_0 = 0$ , a $\beta_1 = 2$ ,
тогда $\beta_1^T = 1/2$ ,
так как мы не хотим загромождать статью деталями оценки p-value определения самих $\hat\beta_k$ , просто возьмем размер выборки побольше - чтобы произвольность генерации данных не вносила отклонений в сравнения $\hat\beta_k$ с $\beta_k$ :

true_beta_1 = 2
std_ey = 1
n_sampling = 1_000_000

rng = np.random.default_rng()

X1 = rng.standard_normal(n_sampling)
Y1 = true_beta_1*X1 + rng.normal(scale=std_ey, size=n_sampling)

Прямая и обратная регрессии на первой выборке

def SLR(X,Y):          # вынесем код в функцию, для переиспользования на второй выборке
    SLR_YontoX = linear_model.LinearRegression()
    SLR_YontoX.fit(X.reshape(-1, 1),Y)

    SLR_XontoY = linear_model.LinearRegression()
    SLR_XontoY.fit(Y.reshape(-1, 1),X)

    beta = SLR_YontoX.coef_[0]
    betaT = SLR_XontoY.coef_[0]
    CorrXY = np.corrcoef(X,Y)[0][1]
    R2 = CorrXY**2
    Dx = np.std(X)**2
    Dy = np.std(Y)**2
    
    return beta, betaT, R2, Dx, Dy

beta_1, betaT_1, R2_1, Dx_1, Dy_1 = SLR(X1,Y1)

Сравнение результатов эксперимента с теорией

сравним регрессионные наклоны с "истинными":

show_df = pd.DataFrame(index=['YontoX','XontoY'])
show_df['"true" beta_1'] = [true_beta_1, 1/true_beta_1]
show_df['SLR beta_1']  = [beta_1, betaT_1]
show_df['вывод'] = ['близко к истинному наклону', 'наклон явно менее выражен']
show_df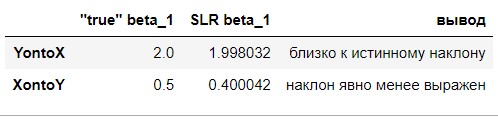

сравним левую и правую части равенств в симметричной системе:

$\left\{\begin{eqnarray}&\hat\beta_1\cdot\hat\beta_1^T &=& \hat R^2 \\&\hat\beta_1\cdot D(x_i) &=&\hat\beta_1^T\cdot D(y_i) \\\end{eqnarray}\right.$

show_df = pd.DataFrame(
              index=['левая часть уравнения', 'правая часть уравнения', 'вывод'])
show_df['первое уравнение системы'] = [beta_1*betaT_1, R2_1, 'полное совпадение']
show_df['второе уравнение системы'] = [beta_1*Dx_1, betaT_1*Dy_1, 'полное совпадение']
show_df.T

Генерация второй выборки: стохастизация только по X, одинаковые дисперсии X и Y

оставим $\beta_0 = 0$ , $\beta_1 = 2$ и прежний размер выборки,
по прежнему $\beta_1^T = 1/2$ ,
обеспечим одинаковую асимптотическую дисперсию в исходных формулах генерации выборки:

std_ex = math.sqrt(true_beta_1**2 - 1) # это обеспечит одинаковую дисперсию по X и Y

Z2 = rng.standard_normal(n_sampling)   # это регулярная часть X
Y2 = true_beta_1*Z2
X2 = Z2 + rng.normal(scale=std_ex, size=n_sampling)

Прямая и обратная регрессии на второй выборке

beta_2, betaT_2, R2_2, Dx_2, Dy_2 = SLR(X2,Y2)  # воспользуемся уже готовой функцией

Сравнение результатов эксперимента с теорией

сравним регрессионные наклоны с "истинными":

show_df = pd.DataFrame(index=['YontoX','XontoY'])
show_df['"true" beta_1'] = [true_beta_1, 1/true_beta_1]
show_df['SLR beta_1']  = [beta_2, betaT_2]
show_df['вывод'] = ['близко к обратному значению','близко к истинному наклону']
show_df

сравним левую и правую части равенств в симметричной системе:

$\left\{\begin{eqnarray}&\hat\beta_1\cdot\hat\beta_1^T &=& \hat R^2 \\&\hat\beta_1\cdot D(x_i) &=&\hat\beta_1^T\cdot D(y_i) \\\end{eqnarray}\right.$

show_df = pd.DataFrame(
              index=['левая часть уравнения', 'правая часть уравнения', 'вывод'])
show_df['первое уравнение системы']= [beta_2*betaT_2, R2_2, 'полное совпадение']
show_df['второе уравнение системы'] = [beta_2*Dx_2, betaT_2*Dy_2, 'полное совпадение']
show_df.T

Заключение по численному эксперименту

Нам удалось в численном эксперименте проиллюстрировать правильность симметричной системы уравнений для прямой и обратной регрессий на одной выборке объектов.
Нам удалось в численном эксперименте проиллюстрировать правильность "пальцевого" объяснения, почему на дополнительное горизонтирование регрессионного наклона влияет только шум по оси X.
При этом манипулируя дисперсией для рандомных членов для генерации X и Y можно добиться отдельного совпадения либо коэффициента прямой регрессии, либо обратной с интуитивно ожидаемым "идеальным" значением.
Также шумами можно добиться совпадения прямого и обратного регрессионного наклона, даже если "истинная" зависимость отлична от 1. Данный вывод сильно обескураживает - предположим, что мы получили результат эксперимента 2 на какой-то реальной выборке: получается, что мы можем только сказать, что истинная зависимость между величинами лежит в промежутке линейного коэффициента от 0.5 до 2.0, причем мы даже не знаем в чью пользу!
Поскольку мы не фиксировали seed при случайной генерации выборки, то числа в таблицах будут немного меняться при повторных прогонах кода, но это не изменит выводы в таблице.

Комментарии (31)

aamonster
00.00.0000 00:00
#25276410
+1
Всё ждал, когда же откроется секрет – как занижается коэффициент регрессии... Прочитал пол-статьи, и тут хоба – обратная регрессия! Интрига выдержана мастерски!
1. SanSanychSeva Автор
  00.00.0000 00:00
  #25276626
  +1
  Так ведь, и в прямой регрессии коэффициент тоже занижается - см. таблицу результатов эксперимента на второй выборке: истинная бета равна 2, а прямая регрессия дала 0.5.
  
  Интрига (для меня, по крайней мере) в том, что обычно при поверхностном изучении темы выборка генерится по первому типу, когда коэффициент прямой регрессии асимптотически равен истинному - но не все понимают, что это вырожденный случай, такая выборка неверно отражает реальные данные: в природе именно этот случай как раз и отсутствует!
  
  Именно поэтому ошибочный вывод о регрессии роста и сделал сэр Фрэнсис Гальтон. Причем, у него эффект должен был быть даже выше на прямой регрессии, так как данные по X (рост отцов) были более старыми, чем по Y (рост сыновей) - то есть, случайных шумов было больше как раз в переменной X !
  
  Я, естественно, не претендовал на новизну - меня больше поразил философский вывод, что даже при коэффициенте существенно отличном от 1 регрессия может дать одинаковый результат в прямом и обратном случае (эксперимент на второй выборке). Собственно, этим удивлением я делюсь с теми, кто проскочил данный факт при самообразовании или на интернет курсах. ISLRv2 не зря вынес его в серию упражнений к главе по линейной регрессии, совсем не упомянув в тексте главы как факт - учеба лучше запоминается, когда тебя проводят через маленькие самостоятельные исследования.
  
  Спасибо за комментарий !
  1. aamonster
    00.00.0000 00:00
    #25277068
    +1
    Да, вторая выборка забавна – как сбалансировать шумы по X и Y так, чтобы завышение коэффициента от первых компенсировало его занижение от вторых)

K_Chicago
00.00.0000 00:00
#25279118
+1
А нельзя ли теперь всё тоже самое но простыми словами и на русском языке?
построение графиков с помощью регрессии делают обычно экспериментаторы, люди простые и практичные. Смотришь, вроде по науке зависимость линейная, берёшь формУлы, хоба - и находишь пересечения с осями, это и все что нужно.
Текст выше написан персонажем купающемся в математических дебрях, типо, математиком для математиков. Это легко и приятно, почти также как говорить правду.
А изложить для тех, кому это нужно так чтобы они поняли - много сложнее, я полагаю. Или нет?
В чем конкретно этот эффект проявляется? Как изменить расчет чтобы сделать на него поправку?
1. SanSanychSeva Автор
  00.00.0000 00:00
  #25279890
  +1
  Отнюдь: текст выше написан как раз физиком. У математика описанный эффект не вызывает шока, так как он следует из формул. А вот меня он сильно удивил.
  
  Ведь именно в физическом эксперименте мы привыкли, что прямая, проведенная по минимальным квадратам по экспериментальным точкам, дает нам экспериментальную зависимость двух "линейных по науке" величин. Причем, мы уверены, что если мы поменяем оси местами, то мы ожидаем, что прямая просто зеркально отразится относительно биссектрисы угла XOY - то есть если Y=2X, то и X=Y/2.
  
  Однако, если вы посмотрите на численный эксперимент на первой выборке, то с удивлением увидите, что асимптотически (при увеличении размера выборки ) регрессионные прямые стремятся к Y=2X, но X=2Y/5 !
  
  Чтобы не было сомнений, я считал коэффициенты наклона регрессионных прямых не по аналитическим формулам, но честным вызовом библиотечной модели линейной регрессии, которая численно находит минимум квадратичной функции потерь - градиентным спуском (численное значение совпадает с аналитической формулой, конечно, - в приведенных ссылках на GitHub я это тоже проверял, если интересно).
  
  Как физик, я дал простое объяснение эффекту в разделе "Объяснение эффекта на пальцах" - оказывается стохастический разброс экспериментальных точек по оси X приводит к возникновению у них горизонтирующего регрессионную прямую вращательного момента.
  
  Поправку от влияния шумов данных на искажение истинной линейной зависимости дает совсем простая система двух уравнений для коэффициентов прямой и обратной регрессий. В частном случае, когда оба коэффициента равны, то они оба оказываются менее 1 - они равны коррелятору <X,Y> (который всегда меньше 1). С этим связан исторический курьез, восходящий к появлению термина регрессии, что означает вырождение, направление, обратное прогрессу: маловероятно, что на протяжении одного поколения рост человека заметно менялся, так что в опыте сэра Фрэнсиса Гальтона истинную линейную зависимость можно считать равной 1, но регрессионный коэффициент получился меньше.
  
  Вы спросите, так как же по экспериментальным прямым понять в каком диапазоне лежит истинная линейная зависимость двух величин - ответ тоже есть в статье: истинный коэффициент лежит между коэффициентом прямой регрессии и обратной величиной коэффициента обратной регрессии. Например, в нашем численном эксперименте истинный коэффициент оба раза был равен 2 - и согласно данному правилу, он лежит в первой выборке между 2 и 5/2, а во второй выборке между 1/2 и 2. Если выборку генерили не мы сами, а жизнь, то мы не можем сказать где именно в этом интервале!
  
  В заключение большое спасибо вам за комментарий - он как раз показал полезность корректировки интуитивных представлений о линейной регрессии у физиков, как я и предполагал на своем собственном примере.
  1. K_Chicago
    00.00.0000 00:00
    #25279944
    +1
    текст выше написан как раз физиком
    
    процитирую кролика - Что значит "Я"? "Я" бывают разные!
    вы знаете, вот Шелдон - физик, но и Говард - физик, и это две большие разницы.
    
    Я помню в ИХФ АН СССР у нас в отделе Гольданского был эпизод: я говорю коллеге - да ты даже каскад правильно расчитать не можешь, теоретик! - он отвечает: да ты сам неправильно собрал, теоретик! - тут встревает свежий аспирант: "ребята, чего вы так страшно ругаетесь??"
    
    Это о "физиках".
    
    Я вынес из вашего ответа, что коэффициенты прямой имеют тенденцию меняться при увеличении выборки - это и есть эффект?
    
    SanSanychSeva Автор
    00.00.0000 00:00
    #25280354
    Хе-хе, ну да, я физик-теоретик (в прошлом), но тем не менее и среди теоретиков были те, кто мог объяснить все просто - Фейнман, например. Увы - мне далеко.
    
    К сожалению, эффект в другом: в общем случае регрессия дает неверное (заниженное) значение коэффициента линейной связи двух физических величин - вы попробуйте поизучать детали опыта автора названия "регрессия" Фрэнсиса Гальтона (все в интернете): ну человек же обнаружил, что если по осям отложить физические параметры в двух поколениях в координатах (X=отец, Y=сын), то у регрессионной прямой наклон статистически достоверно будет меньше 45% - ну в данном случае очевидно, что если не было какой-то катастрофы в этом поколении, то в среднем нет разницы в поколениях отцов и детей - истинная прямая должна быть точно под 45%. Конечно, на больших временах происходит развитие вида, но не в одном поколении!
    
    SanSanychSeva Автор
    00.00.0000 00:00
    #25280472
    Дополнение для Чикаго: кстати, вы и сами можете обнаружить этот эффект без всякого изучения линейной регрессии и методов градиентного спуска - ведь в случае простой линейной регрессии существуют совсем простые аналитические формулы (в случае, если X - матрица, а не вектор, аналитические формулы тоже существуют, но уже в матричном виде). Вы же не по линеечке проводите свои экспериментальные прямые, а подставляете вектора X и Y в известную вам формулу для наклона прямой - так вот поменяйте местами X и Y и посчитайте наклон в обратных координатах - вы удивитесь, что он будет отличаться от 1 делить на наклон в прямых координатах: то есть если вы отложите обе прямые на одном графике, они не совпадут!
    
    Не знаю как еще популярнее изложить.
    
    K_Chicago
    00.00.0000 00:00
    #25280528
    +1
    мы говорим о линейной регрессии, по мнк, правильно? Что такое "коэффициент линейной связи" - это угол наклона прямой? Например, спектрометрическая зависимость поглощения от концентрации. Вы хотите сказать что построеная по мнк прямая показывает коэффициент поглощения меньше, чем "на самом деле"?
    
    SanSanychSeva Автор
    00.00.0000 00:00
    #25280676
    Спасибо за прекрасный пример - отвечаю на нем:
    
    Если существует существенная стохастическая ошибка измерения концентрации - ДА, вы получите рассчетный наклон меньше, чем "на самом деле" ! Это же очевидно, так как те же точки сильнее размажутся по X, чем были бы "на самом деле".
    
    С абсолютным значением поглощения сложнее - поворот же происходит вокруг центра масс экспериментальных точек, то есть при горизонтировании прямой происходит одновременно изменение точки пересечения прямой с осью Y. При этом абсолютное значение поглощения будет занижено для больших концентраций (выше среднего по выборке) и завышено для низких (что ниже среднего).
    
    NB!: Если же концентрация меряется очень точно, то даже при видных невооруженным глазом случайных ошибках измерения коэффициента поглощения, истинный наклон будет практически равен коэффициенту прямой регрессии (это соответствует численному эксперименту на выборке номер 1 в статье).
    
    Однако, предположим, что вы решили использовать полученную экспериментально зависимость для градуировки прибора, который измеряет плотность по поглощению (обратная зависимость): так вот за исключением случая, когда у вас все точки экспериментальной кривой строго лежат на прямой (то есть исключая корреляцию <X,Y> = 1), вам НЕ следует использовать простое деление измеренного коэффициента поглощения на наклон прямой, рассчитанный по прямой формуле на экспериментальных данных, но нужно еще домножить на квадрат коррелятора ваших экспериментальных данных, полученных для градуировки прибора:
    
    (дельта концентрации) = (дельта измеренного коэффициента поглощения) * <X,Y>**2 / (наклон экспериментальной прямой, рассчитанный методом минимальных квадратов по набору {X,Y} ) ,
    
    обратите внимание на дельту - я не говорю об абсолютных значениях, так как изменятся и точки пересечения прямых с осями координат!
    
    Ну или вам сразу нужно считать обратный наклон в координатах (X=поглощение, Y=концентрация) - результат будет тот же, благодаря первому уравнению системы уравнений для коэффициентов прямой и обратной регрессий, цитируемой в статье!
    
    Разумеется, в градуировке прибора это обычно уже учтено и вы видите сразу истинную концентрацию. Но если вы используете прибор в условиях наличия дополнительного фактора, которого не было при его градуировке, но который просто стохастизирует измерения коэффициента поглощения, то прибор даст вам заниженное значение концентрации для значений правее/выше центра масс градуировочного набора данных, и завышенное - для тех, что левее/ниже ! Всегда увеличение ошибки в измерении X даст более горизонтальную линию, повернутую относительно центра масс выборки.
    
    K_Chicago
    00.00.0000 00:00
    #25283046
    +1
    Ваше утверждене понятно.
    
    Но как же быть с тем что подобный метод измерения концентрации является стандартным, общепринятым, применяется вообще везде, включая например и лабораторные практикумы по количественному анализу, где преподаватель дает растворы с точно известной(ему) концентрацией и нужно получить именно это значение в пределах ошибки измерения?
    
    Получается что вообще все "мужики-то и не знали"?
    
    Или вы хотите сказать что эффект имеет практически ничтожное влияние, которое не обнаруживается лабораторными методами?
    
    SanSanychSeva Автор
    00.00.0000 00:00
    #25283098
    Давайте посмотрим - итак, дан раствор с неизвестной студенту, но точно известной препу концентрацией. Студент измеряет коэффициент поглощения методом, у которого большая статистическая погрешность, - ну так и его ответ про концентрацию получит такую же большую погрешность.
    
    Однако вы подменяете задачу - вопрос же найти коэффициент пропорциональности между концентрацией и коэффициентом поглощения. Практический совет такой: нужно строить прямую по экспериментально промеренным точкам методом мнк в координатах, где ось X соответствует параметру с минимальной статистической погрешностью измерения - в нашем случае это концентрация. Тогда наклон мнк прямой будет максимально близок к "истинной" зависимости.
    
    Да, "мужики не знают в массе", что при прямой и обратной линейной регрессии получаются не совпадающие прямые, пересекающиеся в центре масс выборки экспериментальных значений, а истинная линейная зависимость физических величин идет внутри угла, ограниченного этими прямыми.
    
    Но, кстати, и центр масс выборки не точно лежит на истинной прямой - его смещение с истинной прямой в корень из размера выборки раз меньше стандартного отклонения значений самой выборки от этой прямой. То есть, увеличением выборки можно попасть ее центром на истинную прямую, а вот угол разброса при росте выборки не будет стремиться к нулю, но его значение будет приближаться к асимптотическому ненулевому значению - например, в статье в численном эксперименте на первой выборке истинный коэффициент 2 асимптотически лежит между регрессионными значениями 2 и 2.5, но сами границы определяются с точностью порядка обратного корня из размера выборки: то есть при размере выборки в миллион, как в статье, - с ошибкой порядка 0.002. В статье на случайной выборке мы как раз и получили 1.998 вместо 2, но если повторять прогон кода, то это значение будет скакать в пределах ошибки вокруг 2.
    
    K_Chicago
    00.00.0000 00:00
    #25283658
    +1
    Тогда наклон мнк прямой будет максимально близок к "истинной" зависимости.
    
    вот досюда включительно я всё понимал.
    
    А всё после этого - "папа, что это было?"
    
    ну и да, это вовсе не "метод, у которого большая статистическая погрешность", это стандартный фотометр с известной погрешностью, не "большая" и не "маленькая" (что это вообще значит? большая по сравнению с чем?), но погрешность известная и вполне достаточная для большинства количественных измерений.
    
    SanSanychSeva Автор
    00.00.0000 00:00
    #25284688
    Про "папа что это было" - похоже, я исчерпал весь свой скромный навык популяризатора, мой последний совет вам пощупать эффект своими руками, вы же физик-экспериментатор. Возьмите набор экспериментальных точек {(x,y)}, не точно ложащихся на одну прямую, и посчитайте наклон прямой по формуле мнк. Потом поменяйте оси местами и снова посчитайте наклон по формуле мнк. Поскольку смена осей равнозначна отражению относительно оси x=y, то естественно ожидать, что коэффициенты наклона прямых при перемножении дадут 1 (то есть на одном графике дадут одну общую прямую), но на самом деле они дадут квадрат коррелятора <x,y>. Чем сильнее разброс точек от прямой линии, тем сильнее коррелятор просядет от 1, тем больше будет угол между прямыми мнк на общем графике.
    
    Про "относительно чего большая/маленькая погрешность" - точный ответ:относительно промеренного диапазона величины, приблизительный ответ: относительно характерного значения величины. (а то вы не знаете!)
    
    K_Chicago
    00.00.0000 00:00
    #25284940
    Вы себя объявили "популяризатором", мол, объясняю для тупых. Не надо так. Это какой-то утонченный(или не очень) снобизм. Вы упомянули вот св.Фейнмана. Он популяризатор? Нет. Он просто гений с ясным мышлением и ясным изложением. (говорят, когда Ландау объяснял, вообще никто ничего понять не мог).
    Весь сыр-бор из-за раных "ментальностей" теоретика и экспериментатора. Вот Фейнман мог говорить на языке экспериментаторов. Язык называется "физический смысл". Было кажется у Варшавского в фантастическом рассказе космонавт спрашивает про супер-новый космокорабль - "так как же он у вас летает?" - "так вот же формула, видите?" - "не знаю, я на всяких летал - на ионных, на ядерно-импульсных, на фотонных - а вот на формулах не летал!". Это не о том кто глупый а кто популяризатор. Это о способе мышления, диктуемого профессией.
    
    Вопрос "относительно чего большая/маленькая погрешность" не следует понимать буквально (а то вы не знаете!), смысл утверждения (это был по сути риторический вопрос) - погрешность мы (экспериментаторы) считаем "большой" когда "на глазок" не видно, по какому закону распределяются точки. По-простому говоря, если я намерял этакое облачко, слегка например эллиптическое, то проводить через него прямую по мнк - дело дурацкое. А если я намерял в общем приличные точки которые, если прищуриться :)) в принципе ложатся на прямую - вот тогда я достану формУлы и эту прямую просчитаю.
    Это я вынес из моей 25-летней работы в лабораториях (я в общем не физик, я биолог-биофизик) - если эффект на графике не виден на глаз - применение изощренной математики это от лукавого. Я понимаю поднимется плач и вопль от такого крамольного утверждения...но опыт не пропьёшь ;)
    Есть еще такая вещь как "доверительный интервал", так вот из лабораторной практики в физхимии, биохимии - если интервал 65-70%, то это зае<>сь хорошая точность. Лучше не бывает.
    
    SanSanychSeva Автор
    00.00.0000 00:00
    #25285152
    Здоровая жизненная философия! Я только не пойму, как при ней вы так "зацепились" за эту статью - я ж еще в психологическом введении написал, что пока не начнешь считать обратную регрессию и сравнивать с прямой, никакого дискомфорта сомнений в "истинности" коэффициента регрессии не испытаешь. А уж если еще и прямую проводить только там, где она и так по точкам уже видна - то вам и формула для мнк не особо нужна.
    
    (про популяризатора причин обиды не понял - как по мне, это позитивный термин - так что не знаю, что и сказать. Предлагаю также отнести к риторическим темам)
    
    K_Chicago
    00.00.0000 00:00
    #25286472
    А уж если еще и прямую проводить только там, где она и так по точкам уже видна - то вам и формула для мнк не особо нужна.
    
    Ещё один супер-перл. Просто супер. По-моему вы в принципе не понимаете, зачем нужны все эти "мнк" и прочее. Попробую для вас популяризировать. ФормУла нужна единственно лишь для того, чтобы обосновать коэффициенты проведенной прямой. Разумеется, я могу прямую провести "на глазок", и написать в статье мол вот какие коэффициенты. Другой тоже проведет ее на глазок по этим же точкам, но чуть по-другому, и цифры получатся другие. А формУла всего лишь позволяет обосновать мои цифры и гарантирует что у других интересующихся получатся те же цифры, если они используют те же экспериментальные точки. И только. Не больше и не меньше. И, как я уже выше сказал, при этом получить доверительный интервал. Если он в пределах хотя бы 70%, такие измерения осмысленные и будут приняты коллегами. Если сильно меньше - никто так не делает, дураков нету.
    
    Вы серьезно предлагаете использовать регрессионную формулу там, где характер кривой по точкам непонятен? Т.е. если там бесформенное облачко, вы собираетесь провести через него прямую каким-нибудь математическим способом и при этом полагать что полученные цифры имеют физический смысл? Не делайте так пожалуйста.
    
    Приведу другой пример - например, ожидается получение сложной кривой с каким-то (неизвестным) числом экстремумов. Спектр, по-простому. Если экстремумы в принципе на глаз видны, применяют скажем сплайн-аппроксимацию, исходя из ожидаемых результатов задают параметры сглаживания. Чем меньше сглаживание, тем больше экстремумов получится, и тем меньше доверия их точным координатам. А научное сообщество решит, насколько разумно я выбрал эти параметры.
    
    по-вашему "популяризатор - это позитивный термин"? Вы, пардон, или лицемерите...или дела совсем плохи. Или вы также не понимаете что такое "научное сообщество". Классический пример - Капица. Когда он стал мистером "очевидное-невероятное", его авторитет как ученого стал ниже плинтуса. Вот поэтому.
  1. K_Chicago
    00.00.0000 00:00
    #25279968
    +1
    добавлю, простите мне мой клатчский:
    
    горизонтирующего регрессионную прямую вращательного момента
    
    Эта пять!!!
    
    Эта "синекдоха отвечания", не меньше и не больше.
  1. S_A
    00.00.0000 00:00
    #25279982
    +1
    С точки зрения математики, отсутствие "симметрии" для коэффициентов регрессии следует из того шум сгенерирован не во всем пространстве <X, Y>, а только в пространстве X. Кстати привычные реальные данные генерируются не условным, а совместным распределением.
    
    Попробуйте повторить с двумя переменными, т.е. Z = aX + bY + eps. И другой вариант: ln(Z) = тоже самое. Симметрии даже рядом не будет ожидаться. А если генерировать <y + N(0,1), x + N(0,1), z(x, y) + N(0,1)>...
    
    И еще, строго говоря, если y = f(x), x = f-1(y), то не следует что x + eps = f(f-1(x))
    
    SanSanychSeva Автор
    00.00.0000 00:00
    #25280412
    +1
    Спасибо за дополнительные примеры в вашем комментарии!
    
    Да, с точки зрения математики все очевидно, и тут нет никакой научной новизны. Мотивация статьи - адресовать "культурный шок" физиков, которые всю жизнь были уверены, что метод прямой по минимальным квадратам, который они применяли с институтских лаб по общей физике, дает симметричную зависимость: если Y=2X, то и X=Y/2.
    
    Очень показательно почитать комментарии коллеги физика-экспериментатора выше - он великолепно представляет целевую аудиторию этой статьи. Хотя я изначально адресовал ее тем, кто быстро проскочил тему линейной регрессии в своем DA/DS образовании - поэтому язык статьи ориентирован на них.
    
    Для физика мне пришлось провести аналогию с моментом сил, которые действуют на рычаг регрессионной прямой относительно центра выборки - мне и самому так понятнее в силу физической интуиции своего образования. Но будучи еще DA/DS-ом, я также понимаю, что если бы не квадратичность функции потерь, то и эффекта бы не было - например если просто минимизировать среднее расстояние, а не его квадрат: так как в линейном случае вклад от точек на расстояниях +/- дельта от невозмущенного значения ( $x_0 - \bar x - \delta$ и $x_0 - \bar x + \delta$ ) был бы одинаков для линейной функции потерь - не было бы эффекта плеча рычага, говоря языком физиков!

hbrmrk
00.00.0000 00:00
#25280626
+1
Спасибо за статью.

вы попробуйте поизучать детали опыта автора названия "регрессия" Фрэнсиса Гальтона

А вы сами читали? https://doi.org/10.2307/2841583

Во-первых, в статье Гальтон не разрабатывал матаппарат и статья чисто антропологическая, поэтому утверждение

статистически достоверно будет меньше 45%

неверное: p-value там нет, статистических гипотез нет, трёх сигма там нет. Погрешностей там нет. Совет физикам, читающим эту статью в будущем: не приводите значения измеренных физических величин без указания погрешности.

В-вторых, следующее утверждение неверно:

С этим связан исторический курьез, восходящий к появлению термина
регрессии, что означает вырождение, направление, обратное прогрессу:
маловероятно, что на протяжении одного поколения рост человека заметно
менялся, так что в опыте сэра Фрэнсиса Гальтона истинную линейную
зависимость можно считать равной 1, но регрессионный коэффициент
получился меньше.

Вывод статьи следующий:

The average regression of the off spring to a constant fraction of
their respective mid-parental deviations,which was first observed
in the diameters of seeds,and then confirmed by observations on
human stature,is now shown to be a perfectly reasonable law which
might have been deductively foresen

То есть, термин "регрессия" в этом контексте означает, что если у родителей рост выдающийся (в любую из сторон), то они с большей вероятностью будут иметь рост прямого потомка ближе к среднему. Пояснение: если бы потомки были равновероятно выше или ниже родителей для любого роста родителя, то можно было бы выводить трехметровых баскетболистов и полуметровых ездоков для скачек за единицы поколений.

В-третьих, можно попросить дополнить статью, чтобы утверджение

регрессионные прямые стремятся к Y=2X, но X=2Y/5

стало бы значимым? То есть, добавить эти самые погрешности.

P.S: Ниже снимок из статьи, который показывает результат из-за которого весь сыр-бор. Там же показана Y=X прямая

Hidden text
1. hbrmrk
  00.00.0000 00:00
  #25280646
  +1
  Для тех, кто не хочет верить рандому в Интернете, вот видео с другим рандомом в Интернете, в котором есть даже график с точками по поколениям и объяснение термина "регрессия" по данным отцы-сыновья (англ):
  
  https://www.youtube.com/watch?v=lIIZOZqKgfQ
1. SanSanychSeva Автор
  00.00.0000 00:00
  #25280894
  Спасибо за профессиональные дополнения и комментарии!
  
  Я намеренно не стал нагружать статью t-статистикой проверки гипотез, дав просто ссылку на Jupyter Notebook на GitHub, в котором я это сделал (еще раз: https://github.com/SanSanychSeva/Exercises-from-Introduction-to-Statistical-Learning-done-in-Python/blob/main/chapter_03_Linear_Regression/exercise_11and12.ipynb) - фокус статьи на когнитивном диссонансе интуиции физиков, поэтому я подчеркнул, что эксперимент иллюстративный и взял выборку побольше.
  
  Однако, иллюстрация неплохо получилась, а t-статистика только отпугнула бы целевую аудиторию - и так вот коллеги жалуются, что одна математика, хотя я резал ее как мог ! (ну ведь для специалистов в ML в статье же нет ничего нового - если только они сами не проскочили этот факт в свое время)
  
  Я знаю, что у Гальтона речь шла не об уменьшении роста, а о регрессии к среднему росту - простите за неловкие формулировки в спешке ответов. Но согласитесь, если бы кто-то сперва поменял ему данные отцов и детей, его вывод был бы тем же! После чего его можно было бы удивить, сказав где на самом деле были отцы, а где дети.
  1. hbrmrk
    00.00.0000 00:00
    #25280926
    Но согласитесь, если бы кто-то сперва поменял ему данные отцов и детей, его вывод был бы тем же
    
    Пожалуй, не соглашусь. Посмотрите на картинку в комментарии: там есть оси с подписями. Иронично, но она как раз повёрнута на 90 градусов, поэтому представлять проще. На "графике" из работы Гальтона видно, что его данные "на глаз" уходят от Х=У. Более того, повторюсь: "регрессия" в этой работе означает на намеренное занижение коэффициента, а свойство популяции людей в отношении рождаемости, которое и без метода нимаеньших квадратов имеет "физический смысл". Потому что в случае наклона с тангенсом 1 у баскетболиста высотой 2.40 м с одинаковой вероятностью родился бы ребёнок выше или ниже него. А статистика в публикации показывает, что у экстремальных выбросов есть "регрессия к среднему"
    
    SanSanychSeva Автор
    00.00.0000 00:00
    #25281016
    То есть вы хотите сказать, что Гальтон не делает вывод, что со временем разброс роста людей уменьшается, а просто утверждает, что у человека с ростом выше среднего с большей вероятностью рост сына будет меньше роста отца и наоборот, потомок коротышки в среднем нормализует свой рост.
    
    Тогда, мне кажется, ML-коллеги вообще напрасно используют его термин регрессия: получается, он имел ввиду вовсе не линейную регрессию, как трактуют сегодня большинство ML-спецов (например на лекциях Вышки на Ю-тубе), а скорее асимметрию условных вероятностей, направленных к норме.
    
    В споре не только рождается, но и лучше понимается истина - спасибо, что не поленились разъяснить этот момент!
    
    Кстати, а вы уверены, что если поменять данные отцов и детей, то у Гальтона выводы были бы не те же самые? Ведь при такой замене выбросы по росту отцов были бы уже на других объектах. То есть, если взять слишком высоких сыновей или коротышек, то вероятность, что рост их отца был ближе к норме по ним тоже будет выше - разве нет?
    
    hbrmrk
    00.00.0000 00:00
    #25281194
    +1
    что Гальтон не делает вывод, что со временем разброс роста людей уменьшается
    
    Я привёт цитату из статьи. Я не увидел там, чтобы были сделаны далеко идущие выводы насчёт среднего человека
    
    Тогда, мне кажется, ML-коллеги вообще напрасно используют его термин
    регрессия: получается, он имел ввиду вовсе не линейную регрессию, как
    вульгарно трактуют сегодня большинство ML-спецов (например на лекциях
    Вышки на Ю-тубе), а скорее асимметрию условных вероятностей,
    направленных к норме
    
    Не исключаю, что есть эффект сломанного телефона. Надо смотреть каждый конкретный случай и общаться с каждым лектором.
    
    Могу только утверждать, что в статье "регрессия" используется в отношении эффекта в популяции людей и каких-то растительных семян. Касательно термина "Линейная регрессия" в отношении метода, то в статье есть описание того, как этот эллипс на графике был получен. Продираться через такую археологию потребует пол-литра и день-два, но судя по всему, его метод изображения эллипса математически тождественен тому упрощённому рецепту, которым мы сейчас пользуемся.
    
    Как минимум, в аппендиксе есть фраза "Ratio of mean filial regression = 2/3". Может быть с этой фразы данный метод начали называть регрессией, может - нет. Надо звать историков науки.
    
    Кстати, а вы уверены, что если поменять данные отцов и детей, то у Гальтона выводы были бы не те же самые?
    
    Чтобы не было просторов для фантазии: поменял местами данные после обработки автора. Оригинальных данных у меня нет. Тогда можно было бы пофитовать. Может у товарища из видео данные есть
    
    Hidden text
    
    Но если бы данные были перевёрнуты, то это значило, что у высоких родителей вероятность иметь более высокого потомка выше, тем более низкого. (Или более точная формулировка: в данных Гальтона есть больше таких случаев, чем случаев регресси роста к среднему)
    
    На всякий случай проговорю, что этот результат не исключает возникновение высоких или низких людей. Он говорит о том, что есть механизм, удерживающий расползание распределения. Это утверждение я тоже в каком-то курсе по "датасаенсу" слышал. Конкретно не вспомню у кого
    
    P.s: там еще есть прикольные дисклеймеры в конце статьи насчёт того, за что автор не несёт ответственности
    
    SanSanychSeva Автор
    00.00.0000 00:00
    #25281308
    А что - хорошая тема для статьи: разобраться, что же сказал Гальтон, и посмотреть у других исследователей. Мне, чисто интуитивно, кажется маловероятным, чтобы за одно поколение любой видовой параметр "от бога" а не "от людей" так бы менялся, что это было бы заметно невооруженным глазом - ну разве многолетняя катастрофа, типа голода или эпидемии. Интересно, сейчас кто-то ведет такую статистику по росту отца и сына в конкретной паре.
    
    В любом случае - вам еще раз огромное спасибо за подробный корректирующий экскурс и материалы по теме!
1. hbrmrk
  00.00.0000 00:00
  #25281382
  +1
  не разрабатывал матаппарат и статья чисто антропологическая
  
  Поправка: не разрабатывал метод линейной регрессии в том виде, в котором мы его знаем. Обработка данных велась через тепловые карты, как мы сейчас бы сказали.
  
  Гальтон набросал точки на график, потом разбил на квадраты и выписал в каждый квадрат сумму точек внутри. Дальше он обводил обласи, строя изолинии (см стр 255). В результате он увидел, что области имеют вид наклонёных концентрических эллипсов. Именно этот эллипс и изображён на графике под спойлером в родительском комментарии.
  
  А дальше он отдал эти данные компетентному математику Гамильтону Диксону и тот корректно извлёк оттуда параметры эллипса. Гальтон (не Гамильтон) испытал глубокое чувство уважения к математическому анализу, когда получил результаты - это тоже из статьи
  1. SanSanychSeva Автор
    00.00.0000 00:00
    #25281426
    Послушайте, Марк: а напишите вы статью на Хабр про эту историю - ну столько ходит устного фольклора, даже среди специалистов. У вас уже столько фактического материала! Я уверен, всему сообществу будет интересно "откорректировать свои интуитивные представления" об истории термина регрессии и о сэре Френсисе Гальтоне.
    
    hbrmrk
    00.00.0000 00:00
    #25281474
    +1
    Ох, ёлки. Поставлю в туду список. Попробую до конца марта
    
    Мне не хватит матаппарата, чтобы доказать тождественность эих вещей, да и красиво это разжевать для всех. Но чем смогу-тем помогу, если дойду
    
    SanSanychSeva Автор
    00.00.0000 00:00
    #25281730
    Строгость математического доказательства в прикладной статистике не на первом месте - а вот разжевать, это нам важнее!

Об эффекте занижения коэффициента линейной регрессии «шумами» данных, или почему все-таки «регрессия» +6

Введение

Часть первая: Суть и теория эффекта

Психологическая преамбула

Формулы

Некоторые быстрые выводы из симметричности системы уравнений для коэффициентов наклонов кривых

Интерпретация и философские выводы

Объяснение эффекта "на пальцах"

Выводы

Часть вторая: Численный эксперимент

Генерация первой выборки: стохастизация только по Y, разные дисперсии X и Y

Прямая и обратная регрессии на первой выборке

Сравнение результатов эксперимента с теорией

сравним регрессионные наклоны с "истинными":

сравним левую и правую части равенств в симметричной системе:

Генерация второй выборки: стохастизация только по X, одинаковые дисперсии X и Y

Прямая и обратная регрессии на второй выборке

Сравнение результатов эксперимента с теорией

сравним регрессионные наклоны с "истинными":

сравним левую и правую части равенств в симметричной системе:

Заключение по численному эксперименту

Комментарии (31)

SanSanychSeva Автор

SanSanychSeva Автор

SanSanychSeva Автор

SanSanychSeva Автор

SanSanychSeva Автор

SanSanychSeva Автор

SanSanychSeva Автор

SanSanychSeva Автор

SanSanychSeva Автор

SanSanychSeva Автор

SanSanychSeva Автор

SanSanychSeva Автор

SanSanychSeva Автор

SanSanychSeva Автор