
Эта статья из серии постов на тему демистификации ИИ, в которых предпринимаются попытки устранить двусмысленность жаргона и разоблачить мифы связанные с технологиями ИИ.
ChatGPT и другие большие языковые модели (LLM, в дальнейшем БЯМ, короче ЯМ — прим. переводчика) доказали свою полезность для задач отличных от генерации текста. Однако в некоторых областях их эффективность вызывает вопросы. Одной из таких областей является математика, где ЯМ иногда могут предоставить правильные решения для достаточно сложных задачах, в то же время потерпеть неудачу в тривиальных.
Существует немало исследований в которых изучаются возможности и ограничения ЯМ в математике. Недавняя работа проведенная исследователями из нескольких университетов показала, что возможности ChatGPT ниже уровня среднего аспирантов по математике. И отдельное исследование, проведенное профессором Нью-Йоркского университета Эрнестом Дэвисом показало, что ЯМ терпят неудачу при решении весьма простых математических задач заданных на естественном языке.
Эти исследования помогают лучше понять разрыв в решении проблем людьми и глубокими нейронными сетями. Люди и ЯМ могут достигать одного и того же результата в определенных математических задачах, но их методы различаются. И это может оказаться критичным, когда речь заходит о доверии к ЯМ (и другим моделям глубокого обучения) при решении задач требующих планирования и рассуждений.
ChatGPT на поле брани с продвинутой математикой
Математика используется во многих областях науки, включая инженерных и социальных. Специалисты не математики, работающие в этих областях, могут обратиться к ChatGPT, чтобы получить ответы на математические вопросы.
“Поскольку ChatGPT всегда формулирует свои ответы с высокой степенью уверенности, у этой группы людей могут возникнуть трудности с различением правильных ответов от неправильных математических рассуждений, что может привести к принятию неверных решений в дальнейшем”, — заявил в интервью TechTalks Саймон Фридер, исследователь машинного обучения из Оксфорда. “Поэтому важно информировать эти группы об ограничениях ChatGPT, чтобы не возникало чрезмерного доверия к результатам его использования”.
Фридер является соавтором свежей статьи в которой исследуется способность ChatGPT имитировать навыки необходимые для занятия профессиональной математикой. Авторы собрали выборку данных GHOSTS состоящей из задач из различных областей, включая ответы на вычислительные задания, завершения математических доказательств, решения задач математических олимпиад, и поиска в математической литературе.
Задачи были взяты из нескольких источников, включая учебники для выпускников, других математические выборок данных и корпусов знаний.
Их результаты показывают, что ChatGPT выполнил многие задания на проходной балл. Например, что касается вопросов для аспирантов, исследователи отметили, что чат “никогда не показывал не понимания вопроса” (хотя можно поспорить о применимости термина “понимание” к ЯМ), но выдавал ошибочные ответы. Фридер считает, что ChatGPT особенно заметно терпит неудачи в задачах, которые “требуют изобретательных доказательств”, таких как на олимпиадах.
Чат также продемонстрировал очень плохие вычислительные способности. “Даже вычисление простых интегралов (первообразных) может быть затруднено, поскольку ChatGPT часто правильно находя функцию для первообразной упускал константу интегрирования”, — сказал Фридер.
Одним из интересных выводов сделанных в статье является несоответствие между различными уровнями решения проблем. Например, в задачах с дырами в доказательствах (нашел статью на эту тему — прим. переводчика) исследователи обнаружили, что ChatGPT часто “с легкостью выполняет сложные символьные задач”», но во многих случаях не справляется с базовой арифметикой или перестановкой выражений.
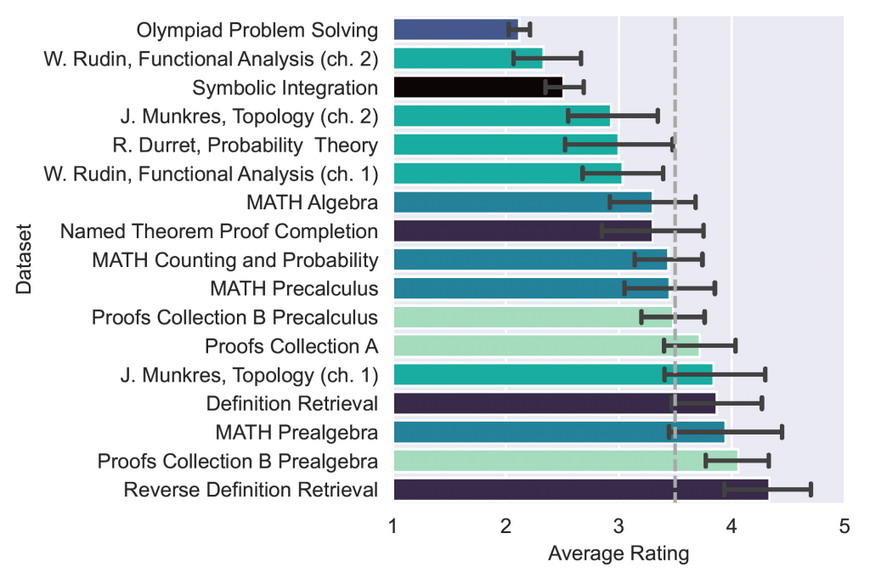
Средний рейтинг для каждого набора данных (одинаковые цвета указывают на то, что файлы взяты из одного и того же набора данных). Поскольку максимальный рейтинг равен 5, а минимальный при котором вопрос был хотя бы понят равен 2, проходной балл (50% баллов) будет равен 3,5, как указано пунктирной линией. Столбики ошибок представляют 95% доверительные интервалы. Источник — Figure 2.
“Нет области математики, в которой вы могли бы полностью доверять выводам ChatGPT (это справедливо и за пределами математики, из-за стохастической природы языковых моделей)”, — сказал Фридер. “Это общее ограничение языковых моделей заключающееся в том, что не существует строгих подходов гарантирующих корректность вывода, от чего также страдает ChatGPT”.
Одной из проблем этого чата является его уверенность в ответах, даже когда он терпит неудачу и использует ошибочную логику. Это очень затрудняет его использование в качестве надежного источника математических знаний.
“Кажется справедливым сказать, что ChatGPT непоследовательно плох в продвинутой математике: в то время как его рейтинги падают с математической сложностью вопроса, в нескольких случаях он действительно дает проницательные доказательства”, — пишут исследователи.
А как он справляется с элементарной математикой?
В другой недавней статье Эрнест Дэвис исследует возможности и ограничения ЯМ в решении таких задач, как эта: “У Джорджа есть семь пенни, десятицентовик и три четвертака. У Харриет есть четыре пенни и четыре четвертака. Сначала Джордж дает Гарриет тридцать один цент мелочью; затем Гарриет возвращает ему ровно половину своих пенни. Сколько денег сейчас у Джорджа?”
Это простые задачи с тремя свойствами: они требуют элементарных математических навыков, сформулированы на естественном языке и предполагают понимание здравого смысла.
Дэвис тестировал три различных подхода. В первом ЯМ просили напрямую выдать ответ. Второй подход заключался в том, чтобы модель генерировала программу, которая решает задачу. И третий — выводила формализованное представление, которое можно было ввести в систему автоматической проверки теорем. ЯМ плохо работали во всех трех подходах, хотя результаты были несколько лучше, когда их просили сгенерировать программу, которая может решить задачу.
Итак, если ЯМ не могут выполнять задания из элементарной математики, почему они демонстрируют замечательные результаты в тестах, разработанных для оценки математических навыков ИИ?
ЯМ добились заметного прогресса в лингвистике, в меньшей степени в здравом смысле и математике. Но, как указывает Дэвис в своей статье, ЯМ плохо умеют сочетать несколько навыков. Например, они в целом “гораздо хуже справляются с задачами, включающими две арифметические операции, чем с теми, которые требуют одной, как в задачах со словами, так и в чисто числовых”.
Одно из важных замечаний Дэвиса заключается в том, что математические критерии разработанные для оценки систем ИИ взяты из тестов созданных для людей. Это может приводить к вводящим в заблуждение выводам. У людей базовые навыки становятся фундаментом на котором мы развиваем более продвинутые. Так, например, если человек может решать дифференциальные уравнения можно ожидать, что он будет не плохо ориентироваться в линейной алгебре.
Но модели машинного обучения, такие как ЯМ, иногда могут находить ответы на сложные проблемы не приобретая тех же навыков, что и люди. Это может быть связано с тем, что ответы находятся непосредственно в обучающих данных (особенно когда модель обучается на очень большом корпусе данных). Или, что модели обнаруживают закономерности, которые могут приводить к правильным ответам во многих случаях, но не всегда.
“[ЯМ] не могут надежно охватить ни одну область математики или какой-либо ее продвинутый раздел”, — сказал Дэвис TechTalks. В то же время “Вероятно, нет такой области математики, в которой вы никогда не получите правильного ответа, потому что иногда они могут выдать ответы, которые были в обучающей выборке”.
Интересно, что Дэвис находит некоторые из тех же видов несоответствий, которые были отмечены и в предыдущей работе. Например, в то время как ChatGPT часто решает базовые и промежуточные математические задачи, иногда он терпит неудачу в очень простых задачах, таких как простой подсчет (возможно это связано с вероятностным выбором механизма сэмплирования модели, см. объяснение в этом переводе с примерами кода; поэтому при повторном запуске задачи в новой сессии возможно получение правильного ответа — прим. переводчика).
“Мое собственное ощущение таково, что если ЯМ не может решать простые арифметические задачи, то на самом деле нет особого смысла спрашивать насколько хорошо она справляется с задачами по теории мер, топологии или абстрактной линейной алгебре”, — сказал Дэвис.
В поиске математических знаний
В тестах, которые провели Фридер и его коллеги, в которых ChatGPT показал особенно хорошие результаты были поиск текста по определению и обратный поиск определений по тексту запроса. По сути, он может служить очень хорошей поисковой системой для получения математических знаний, предоставляя описание тем и сопоставляя описание с основной концепцией.
“[ChatGPT] особенно хорошо работает в качестве математической базы знаний: его можно использовать для эмуляции математической поисковой системы и для получения различных фактов о более сложных объектах”, — сказал Фридер. “Например, я сам узнал о представлении, которое называется ‘расплывчатой топологией’, входящем в более общее представление о слабой топологии. Сначала выбор слова показался странным, и я подумал, что это галлюцинация чата, пока не поискал в Интернете и не узнал из Википедии, что ”расплывчатая топология" — правильное название для конкретного математического объекта."
Дэвис соглашается с тем, что ChatGPT и другие ЯМ могут быть хороши в подборе текста, что также наблюдается в других областях, таких как стандартизированные научные тесты. Но он также отметил, что еще предстоит выяснить насколько они сравнимы на практике с подобными возможностями Wikipedia и Mathworld, особенно поиске определений и обратном поиске определений.
Для обратного поиска определений необходимо проверить насколько устойчива их система к переформулировкам определений из стандартного учебника, как сохраняющим смысл, где они должны быть успешными, так и изменяющим смысл, где они, предположительно, не должна быть успешными, и в идеале должны выдавать какое-то предупреждение”, — сказал Дэвис.
Точно настроенные ЯМ
В своей статье Фридер и его коллеги обнаружили, что модели глубокого обучения, разработанные для решения математических задач или ЯМ настроенные на больших математических выборках данных, гораздо более точны, чем ChatGPT.
Одна из выдающихся работ — это модель глубокого обучения, разработанная исследователями ИИ Facebook Гийомом Ламплом и Франсуа Шартоном в 2019 году. Они создали систему для генерации обучающих наборов данных для контролируемого обучения интегрированию и дифференциальным уравнениям первого и второго порядка. Затем они обучили трансформаторную модель на этой выборке данных. Результаты их тестирования показали, что эта модель работает лучше, чем программы алгебры на основе правил, такие как MATLAB и Mathematica.
Вторая модель — Minerva, большая языковая модель от Google, предварительно обученная на общих данных естественного языка и доработанная на данных устных математических задач, конкурсных математических заданиях, а также задачах из разных областей науки и техники. Как и ожидалось обе модели превзошли ChatGPT в решении математических задач.
«Тонкая настройка на большем математическом наборе данных, вероятно, увеличила производительность», — сказал Фридер.
Дэвис также согласился с тем, что точно настроенные трансформаторы, подобные разработанному Лэмплом и Чартоном, могут “иногда находить решения проблем, которые отсутствуют в стандартных системах, таких как Mathematica”. Но он отметил, что “те проблемы, которые смогли решить эти системы, почти никогда не представляли действительного математического интереса”. “Это может измениться”, — добавил он.
Дэвис также отметил, что было несколько реальных случаев, когда системы ИИ были полезны математикам, включая систему глубокого обучения, которая обнаружила быстрые алгоритмы умножения матриц, и несколько систем, которые смогли помочь в теории графов. “Но такого рода помощь в значительной степени случайна”, — добавил он.
В перспективе предстоит еще много работы
В этой области еще много возможностей для открытий. При более точной настройке эти системы однажды могут стать надежными помощниками для людей не имеющих высшего образования в области математики. Но пока стоимость оценки результативности математических выводов ЯМ непомерно высока.
Фридер и его коллеги открыли исходный код своего набора данных и фреймворка, который включает подробную систему оценки выходных данных модели и достоверности, коды ошибок и предупреждений, а также комментарии рецензентов. Процесс сбора и анализа данных потребовал ручной работы экспертов и не мог быть передан на аутсорсинг через такие платформы, как Amazon Mechanical Turk. Сделав его общедоступным они хотят “побудить сообщество вносить свой вклад и расширять эти наборы данных, чтобы их можно было использовать в качестве полезного ориентира для других ЯМ”, как пишут сами исследователи.
Фридер и его соавторы также работают над новой статьей, в которой будут представлены результаты исследования возможности автоматического выполнения математики исключительно с помощью ЯМ. “Это даст эмпирический ответ на старый вопрос о том, нужно ли формализовать математику или нет, чтобы выполнять автоматические доказательства теорем”, — сказал он.
Комментарии (37)

NeoCode
00.00.0000 00:00+1Языковая вероятностная модель разумеется не предназначена для точной математики, там нужна именно математическая модель. Да, наверное какая-то логика в вероятностной языковой нейросети имеется, но она появляется там как побочный продукт огромного объема входных данных и размазана весьма тонким и неравномерным слоем. Это не то, чему можно безоговорочно доверять, как доверяем мы например арифметическим операциям в процессоре.
Вообще, языковая модель в моем представлении - это лишь мостик между несоврешенным человекоориентированным представлением информации и более совершенным AI-ориентированным, существующим в более формальном виде, подобно тому как формулы существуют в системах символьной алгебры. Это очень важный мостик, ибо перегнать вручную весь огромный объем знаний, накопленный человечеством, в машинно-ориентирванную форму, кажется практически невозможным (хотя прецеденты есть: тут на Хабре были статьи о формализация математики, о попытках создания онтологической базы знаний и т.п.). С помошью ИИ мы сделаем это достаточно быстро. И это важнейшая задача на сегодня - формализация знаний. Нельзя останавливаться на языковом уровне, нужно идти дальше, и языковые ИИ в этом деле отличные помощники, но не конечная цель или конечный результат развития ИИ как такового.

N-Cube
00.00.0000 00:00+1Математика вовсе не настолько формализованная наука, как многие думают. К примеру, Ньютон и прочие физики вообще не формализовали понятие бесконечно больших и малых величин, а оперировали ими интуитивно, как реально существующими величинами. Ну а после формализации (как предела последовательности) это определение оказалось совсем уж противоречащим физике (нельзя взять количество вещества менее одной молекулы) и пришлось для физики возвращаться к старому (см. аксиому Архимеда), а математике заниматься формализацией дальше. В итоге, сегодня для физика и математика понятия бесконечно малого кардинально отличаются, и классические учебники физики с точки зрения современной математики вообще не содержат никаких строгих доказательств. Да и в чистой математике все еще нет строгих формальных доказательств всего того, что ранее доказано менее строгими методами. А что делать с чисто вычислительными доказательствами, когда формального доказательства найти пока не удалось или это вовсе не возможно?

NeoCode
00.00.0000 00:00Все эти нюансы можно и нужно учитывать при формализации и построении онтологий. Вот прямо так - отдельно "физическая бесконечно малая", отдельно "математическая бесконечно малая", для них обобщение "просто бесконечно малая", к этим понятиям уже цепляются еще более неформальные языковые формы, и т.д.
Я лишь говорю о том, что языковая вероятностная модель - самая неудобная для науки, потому что она основана на интернет-болтовне миллиардов людей, и по сути ничего кроме этой болтовни воспроизводить не может. Вместо Сингулярности мы построим совершенную болталку, которая будет писать нам идеальные художественные книги, снимать идеальные художественные фильмы, но ни на шаг не приблизит нас к решению фундаментальных вопросов и задач Физики, Биологии и Всего Такого.

domix32
00.00.0000 00:00Математика вовсе не настолько формализованная наука
Думается тут должно быть "не настолько формализованная насколько хотелось". Ну и физика оперирует по большей части с реальным миром, а мат.аппарат тут просто как инструмент. Тут ни число грэхэма не увидеть, ни поработать с сюрреалистичными цифрами - эмпирические данные к ним никак не ведут, так что не удивительно, что какие-то вычисления различаются.
вообще не содержат никаких строгих доказательств
так потому что как доказать, что небо действительно синее. Это наблюдаемые данные и физика пытается найти законы для них, а не доказать верность чего-либо. А т.к. нет полной информации, то и многие модели работают тоьлко до определённых моментов.
А что делать с чисто вычислительными доказательствами
вот тут надо уточнение, что под этим подразумевается. типа как оценка, что "почти все" числа статистически закончатся циклом в единице в гипотезе Коллаца?

N-Cube
00.00.0000 00:00Вообще-то математика позиционируется как общий язык всех наук, но после формализации она этим языком быть перестала, а появилось несколько лишь частично совместимых диалектов. Более того, существование математики разной строгости приводит к тому, что мы уже не знаем, что же считать доказанным (например, часть формальных доказательств настолько сложны, что достоверными их считать нельзя). А еще есть вычислительная математика, со своими заморочками типа неоднозначности представления чисел с плавающей точкой, сходимости именно вычислений и так далее. Очевидно, что пока мы не смогли даже математику как таковую формализовать, про формализацию вообще всех знаний не может быть и речи…
С небом-то как раз все ясно - рассеяние Рэлея для видимого диапазона дает 16 раз (2 в степени 4) разницу интенсивности рассеяния с максимумом в сине-фиолетовой области (но фиолетовый мы плохо видим), так что рассеянный синий свет и «окрашивает» небо. Кстати, GPT-4 сегодня проверил на этом вопросе - ответила, а вот предыдущая версия GPT-3.5 даже с наводящими вопросами про четвертую степень длины волны (частоты) ничего сказать не может (вчера пытал, формулу приводит, но «сообразить» в чем там дело, не умеет).
Гипотеза Коллатца про сходимость рядов почти наверняка имеет аналитическое решение, а вот что делать с задачей о четырех красках, к примеру?

domix32
00.00.0000 00:00Общим языком для всех наук отродясь была философия, а не математика. Из неё выделились логика и от неё уже стали плясать все остальные науки. Именно из логических постулатов стали появляться доказательства, формироваться аксиомы и теоремы. Она никогда не была общим языком. Однако в древние времена большинство дисциплин не были строго определены в принципе и остатки этого до сих пор есть в той же болонской системе, когда люди защищают свою степень доктора философии.
Второй момент - математика всегда стремилась абстрагироваться как можно сильнее и делала это достаточно успешно всё известное нам время её развития. Физика, химия и прочие использовали математику в прикладных целях в некоторых ограничениях, заданных реальным миром. Потому что чисто математические решения имеют иногда бесконечные траты на вычисление чего бы то ни был. Для реального мира такая точность попросту не нужна и нереализуема. Поэтому есть "несистемные" диалекты математики.
так что рассеянный синий свет и «окрашивает» небо
Это объяснение почему, а не доказательство. Будь я смертоносной глубоководной креветкой, то, взглянув на небо своими 18 видами колбочек, мог бы с большой увереностью сказать, что не очень-то оно и синее, а какое-нибудь шумно-белое, потому что мне тут ешё часть ультрафиолетового и ИК спектра в глаза затекает. Притом отношение катетов к гипотенузе для меня осталось бы таким же как если бы я остался человеком.
Гипотеза Коллатца про сходимость рядов
вы тут на GPTшли какую-то новую гипотезу, про которую никто не знает. В той самой гипотезе Коллатца нет никаких рядов. Да и для решения её вангуют необходимость изобретения какой-то новой математики в теории чисел, т.к. пока ни у кого нет никакой интуиции, как к подобным задачам подступаться. Вообще, вопрос был что вы зовёте "вычислительными доказательствами"? Есть несколько задач, которые были доказаны для некоторых чисел, а всё что находилось за пределами доказанного проверялось на компьютере - например, единственное разложение на простые множители - было доказано, что после определённого порога оно точно имеет единственное разложение, а до самого порога досчитали на машине. Это вы называете вычислительным доказательством?
Есть ещё вычислимая математика, когда логические утверждения строятся на булевых секвенциях и индукции/дедукции, представимых на компьютере и широко используемый во всяких Coq/Lean и прочих логических ЯП и SAT-solverах. И это пока что наисильнейший способ формализации. Который естественно имеет свои ограничения. Точность представления им особо не мешает, поэтому я так понимаю вы не про это.
N-Cube
00.00.0000 00:00Ну вы и понаписали. Вы серьезно хотите законы Ньютона, к примеру, приравнять к философии? Или все-таки формулы там не блажь, а необходимость, и они как раз передают смысл?
Синий цвет неба доказывается формулой рассеяния Рэлея и диаграммой восприимчивости нашего глаза, я перечислил оба фактора. Но вы зачем-то приплели креветку, у которой диаграмма восприимчивости другая. Не стоит так передергивать.
Причем тут чатгпг, если гипотеза Коллатца предсказывает свойства функциональной последовательности. Почти наверняка, если удастся это к сходимости соответствующего ряда свести, то и аналитическое решение найдется.
Про вычислительные доказательства я вполне ясно написал - теорема о четырех красках. Аналитического доказательства, насколько мне известно, все еще не существует, и может быть не найдено никогда. Тем не менее, теорема доказана. Что ее, в угоду вам отменять предлагаете?

phenik Автор
00.00.0000 00:00Вы серьезно хотите законы Ньютона, к примеру, приравнять к философии? Или все-таки формулы там не блажь, а необходимость, и они как раз передают смысл?
Вот этот момент тонкий и носит методологический характер. Теории, включая кл. механику Ньютона, состоят из концептуальной модели, и соответствующей ее математической, или формальной модели. Концептуальная модель, это смесь эмпирических фактов не объясняемых предыдущей теорией, элементов предыдущей теорией и некоторых метафизических посылок. Формальных моделей теории удовлетворяющих концептуальной может быть много. Они эквивалентны. Кроме того на эти модели накладывается ограничение сводится к формальным моделям пред. теорий в некотором предельном случае в духе принципа соответствия. Это известно для ТО, КМ, и других современных теорий. Для классической такого сведения к аристотелевской фактически нет, т.к. та была не формализованной, а имела наблюдательный характер. Концептуальная модель кл. механики описана здесь, формальные упомянуты выше, их 4, на самом деле больше. Для КМ их девять, судя по этой статье, там же и для кл. механики перечислены. Метафизика, т.е. фактически философия, кл. механики состоит в предположении абсолютности пространства и времени. Это чисто умозрительные предположения, которые невозможно было доказать экспериментально в то время, или опровергнуть. И так в любой физической теории.

N-Cube
00.00.0000 00:00Это все имеет смысл относительно людей - то, как мы вообще теории создаем и их проверяем. А с точки зрения чистой математики - берем, к примеру, все варианты метрического тензора и исследуем, тут и геометрия Евклида и геометрия Минковского появятся без каких-либо психоделических (философских) предпосылок.

domix32
00.00.0000 00:00Вы серьезно хотите законы Ньютона, к примеру, приравнять к философии
Можем приравнять законы Ньютона к чему угодно, что бы это не значило. Сами законы могут быть быть представлены, как математически, в виде формул, так и в виде некоего философского утверждения (все эти "сила действия равна силе противодействия" и прочие). Одно требуется для расчётов, другое для понимания и передачи смыслов, в том числе и между дисциплинами.
Синий цвет неба доказывается формулой рассеяния Рэлея
Опять же, не доказывается, а вычисляется исходя из эмпирических данных для конкретной разновидности глаз без учёта дальтоников. Для того чтобы доказать нужно ещё выстраивать аксиоматику касательно того, что считать синим цветом и непосредственно выдвинуть некоторую гипотезу. А то получится именно как с креветкой - рассеяние тоже, но цвет не тот. Стороны треугольника при этом всё ещё продолжают соотношаться как и прежде для обоих видов, что должно было в прошлый раз намекнуть на свойства теорем/гипотез - абстрагирование от субъекта.
Про вычислительные доказательства я вполне ясно написал - теорема о четырех красках.
Нет, не ясно, потому и переспросил. И примерно довольно неудачный, т.к. доказательство вполне легитимное: нельзя построить граф-контрпример, которые бы не сводился бы к одной из нескольких десятков сотен конфигураций, которые точно раскрашиваются в 4 цвета.
Для любопытных танкистов
Теорема о четырех красках гласит, что любой планарный граф можно раскрасить в четыре цвета таким образом, что никакие соседние вершины не будут одного цвета.
Большая часть теоремы была сформулирована на двух механизмах
- неизбежное множество - набор минимальных карт (графов), удовлетворяющих свойству 4-нераскрашиваемой триангуляции.
- сократимая конфигурация - такое расположение вершин, которое не является минимальным контрпримером.
В ходе доказательства был сформирован набор из 1000+ неизбежных конфигураций, который проверялись на нераскашиваемость при помощи компьютера. В итоге компьютер выдал 400 с лишним страниц доказательств для этого набора конфигураций, что все они были сократимыми и/или 4-раскрашиваемыми. Позднее результаты компьютера проверялись другими математиками вручную.Но категорию проблем я понял правильно.
Что ее, в угоду вам отменять предлагаете?
я где-то что-то предлагал отменять?
Почти наверняка, если удастся это к сходимости соответствующего ряда свести, то и аналитическое решение найдется.
Был неправ. Действительно существовали попытки найти аналитические решения в диадических числах.

vkni
00.00.0000 00:00Со времён Ньютона прошло достаточно много времени, вообще-то. И последние лет 100 люди работали над формализацией очень сильно.

stt_s
00.00.0000 00:00Лично я от него узнал, что теорема Ферма не является на 100% доказанной, и существуют и другие точки зрения на этот вопрос

BigBeaver
00.00.0000 00:00+5Какой-то очень длинный и сложный способ сказать "нет"

phenik Автор
00.00.0000 00:00+1Ну как? Он же, что-то правильно решает) Просто так не отмахнешься. Может ему количества параметров не хватает только, или архитектуру подправить. Поклонники утверждают, что ЯМ могут генерализовать, находить закономерности, аппроксимировать результаты, и тп.

BigBeaver
00.00.0000 00:00+1Ну так вопрос-то был "можно ли доверять" а не "можно ли в принципе хотя бы иногда получать верный ответ".

phenik Автор
00.00.0000 00:00Согласен, но вопрос о причинах такого недоверия остается, и не автор статьи, не респонденты в своих исследованиях этот вопрос фактически не затрагивают. Адепты этой технологии упирают на то, что это временно, добавим в трансформеры параметров, увеличим производительность оборудования, объем обучающей выборки и улучшим способ обучения и эти проблемы с математикой отпадут. Конечно это как-то поможет, но решит проблему приближенно, как это происходит у человека?
На мой взгляд модельной ситуацией является сравнение обучения математике детей и ЯМ. Дети при обучении числам и операциям с ними опираются на нативное чувство численности, и делают соответствующие обобщения, вырабатывают навыки вычислений на конечном числе примеров. Но могут потом применять их в разных контекстах, и для любых чисел и операций с ними, а их бесконечное множество. Тут, как кажется принципиальная разница, которая не устраняется упомянутыми мерами, а требует совершенно других архитектурных решений. В этом коменте подробнее написал об этом. Автор той статьи так и не ответил, хотя до этого пытался возражать.

BigBeaver
00.00.0000 00:00Вроде, нет. Результату недетерминированной модели априори нельзя доверять.
Дети такая же мясная нейросеть, и им точно так же нельзя доверять.
Это, кстати, не только про математику а вообще. Мне, кстати, тоже нельзя доверять. И вам.
phenik Автор
00.00.0000 00:00Результату недетерминированной модели априори нельзя доверять.
Дети такая же мясная нейросеть, и им точно так же нельзя доверять.Опять согласен, но не забываем, что трансформеры, служащие базовой архитектурой GPT, являются прямыми сетями, а нейросети мозга исключительно рекуррентные. А рекуррентным сетям присущи аттракторы, стабильные динамические состояния. Пример исследования в применении к мозгу. Это уже больше определяет детерминированное поведение, включая психики.

BigBeaver
00.00.0000 00:00Согласен. Но все равно для серьезных задач с высоким требованием к доверию требуется арбитраж в лице нескольких нейросетей.

ChaoticSys
00.00.0000 00:00Что-то я с задачкой про пенни засыпался. "Половина всех пенни" — это вообще половина всех имеющихся у девочки денег — или как?
Человеки, помогите!
domix32
00.00.0000 00:00+1Скорее всего половину имеющися у неё пенни после передачи. То бишь 25х1+1х6 ей отдали и 1х4 её собственные. Итого 1х5 отдала обратно. У джорджа стало 1х1 + 10х1 + 25х2 + 1х5

ChaoticSys
00.00.0000 00:00Ого, задача была глубже, чем я думал — нужно было узнать, какими монетками рассчитался Джорж!
Кстати, Бинг АИ решил, что Генриет отдала два пенни из имеющихся у нее четырех.
domix32
00.00.0000 00:00+1Десятки и четвертаки неспроста появились. Хотя в английской интерпретации с этим конечно попроще - там penny, nickel, dime и quarter - явно обозначения номиналова.

Refridgerator
00.00.0000 00:00У кого есть доступ — может спросить, чему, например, равен интеграл от гауссианы, её Фурье-образ и разложение в степенной ряд? Задачи на сложение уровня первого класса не особо впечатляют.

N-Cube
00.00.0000 00:00Так и вы спрашиваете про известный факт. Ну вот ниже ответ GPT-4:

В формулах чат порой врет, но объяснения выглядят неплохо, например, про 4ю степень рассеивания и цвет неба уже дает пояснения (хотя неплохо бы еще и посчитать соотношение для границ видимого диапазона), волновые функции водорода и так далее.

BigBeaver
00.00.0000 00:00но объяснения выглядят неплохо
Когда верные.
N-Cube
00.00.0000 00:00Как раз таки и не верные утверждения звучат убедительно, в том и проблема. То есть распознать правильный ответ нельзя, не зная его априори.

BigBeaver
00.00.0000 00:00Там было "неплохо". Но да, согласен. И в этом вижу основную проблему с этой фигней. И так-то уже копирайтерский бред тяжело разбирать, а сейчас они в сто раз больше будут писать с помощью этой штуки.

N-Cube
00.00.0000 00:00«Неплохо» в смысле убедительно. Кстати, с переводами еще интереснее - оно не просто переводит, а дописывает свой текст с пояснениями, зачастую ошибочными. И надо очень внимательно вычитывать, чтобы это обнаружить - стиль текста сохраняется и найти такие вставки очень трудно.

Refridgerator
00.00.0000 00:00Так неправильный же ответ. А про Фурье-образ спрашивали?

N-Cube
00.00.0000 00:00Нет, не спрашивал, я уже на волновой функции водорода и прочих рассеяниях потестировал, мне хватило. Правильный ответ получить не удается, притом при запросе уточнения какие-то рандомные формулы показывает, каждый раз разные. А если ссылки запросить - ни одной адекватной нет, часть придумана, а все остальные вообще не в тему. Зато с теоремой Пифагора все ок, так что для школы, вероятно, годится. При переводе система еще и свой текст дописывает, притом порой совершенно неверный, жаль, не показывает, откуда все это берет или как генерирует.



N-Cube
Ну, до математики даже на школьном уровне там очень далеко. К примеру, объяснить задачу трех тел для школьника может без формул. Или рассказать, почему небо синее и рассеяние Рэлея назвать, зато формулы выдуманные, как и ссылки на литературу, так что коэффициенты некорректные и числитель со знаменателем перепутаны, если верить такой формуле то получается, что рассеивается красный свет больше, чем синий и небо должно быть красное. На уточняющий вопрос про сечение рассеяния выдал почти верное выражение, но площадь сферы там с точностью до коэффициента. Похоже, что формулами система оперирует так же вольно, как и текстом. Зато текст хорош, при запросе «для школьника» расписано внятно и растолкованы даже базовые термины, которые человеку и в голову не придет пояснять (гипотенуза и катеты, сечение рассеяния, и так далее). Притом, средний школьный учитель вообще вопроса не поймет, а подобные перепутанные формулы и студенты-физики еще как генерят на экзаменах (со временем начинают соображать и проверять размерности, да и то не все и не всегда), да и в профессиональных изданиях подобные ошибки в формулах встречаются.
BigBeaver
N-Cube
Математика тоже язык и правила известны.
vkni
Как раз таки там, где математика — это язык и правила известны, давным давно работают верификаторы и т.д.
vkni
Это же Физика, а chatGPT — это система, запертая в интернете. Школьнику так или иначе, но приходится проводить годы в реальном мире, несмотря на все его попытки остаться в TikTok'е.
Поэтому, собственно, механику все, кто успешно дожил до 6 класса, интуитивно знают. Ну, как-бы, без интуитивного понимания правила рычага вы останетесь без пальцев, без интуитивного понимания кругового движения — разобьётесь на велосипеде, без интуиции в области потенциальной и кинетической энергии — сломаете себе шею, выпав из окна.
chatGPT же вынужден получать эти знания «из книг и разговоров».