1. Статистический ансамбль

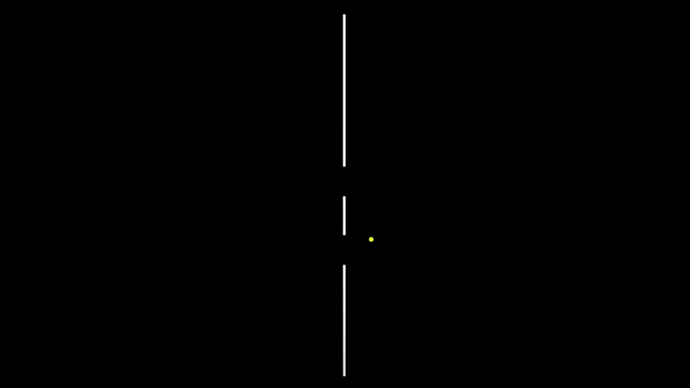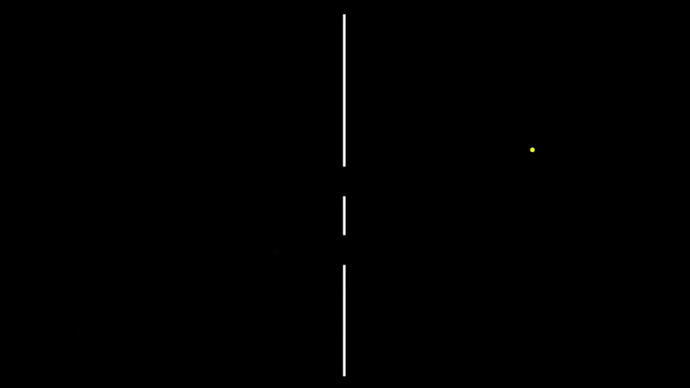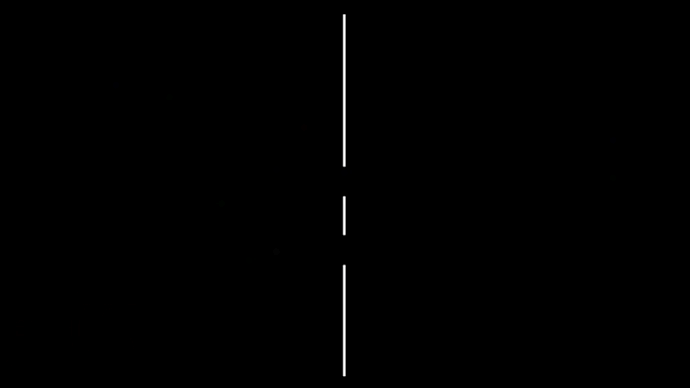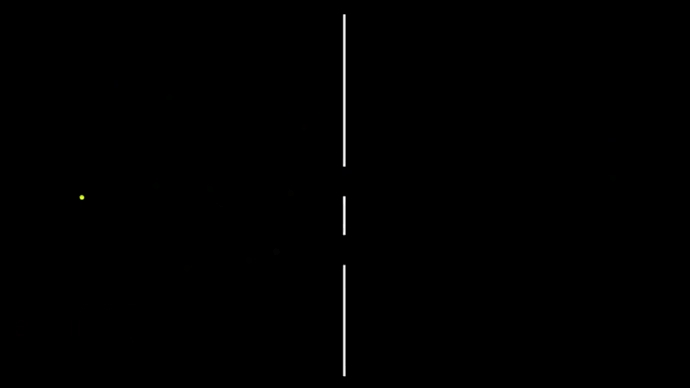
Предположим для начала, что элементарные частицы ведут себя как обычные шарики и посмотрим, что при этом получается, а потом сравним с поведением по законам квантовой механики. Например, внизу на гифке 1 показано излучение такой частицы-шарика гораздо более массивной частицей. Процесс аналогичный излучению фотона атомом можно сказать или вылету электрона из атомного ядра, только с точки зрения классической физики.

При этом предположим, что белая частица излучается с равной вероятностью в любом направлении и при этом со случайной скоростью в диапазоне от нуля до некоторого максимума скорости и в случайный момент времени в некотором определённом временном промежутке. Четыре примера такого случайного вылетания показано на гифке 1.

Если бы это была большая макроскопическая частица, то мы могли бы её непосредственно видеть. То есть каждую секунду от такой частицы-шарика отражались бы миллионы фотонов и прилетали к нам в глаза, и мы могли бы проследить всю траекторию этой частицы от начала до конца. Мы бы сразу видели, в каком направлении она излучилась, и смогли бы определить её скорость и координату. Зная начальную координату и скорость, мы могли бы, используя уравнения Ньютона, рассчитать дальнейшую траекторию частицы, например, при движении в гравитационном поле, или какой либо другой ситуации.

Но что делать, если частица настолько маленькая, что она летит без взаимодействия с другими частицами? При этом мы никак не можем знать направление её вылета и скорость точно, процесс излучения ведь случайный и никак посмотреть на частицу мы тоже не можем. Мы знаем только точку, откуда она испускается, знаем, что испускается в случайном направлении и со случайной скоростью. Значит, теперь мы уже не можем сказать, куда именно она полетит, так как не знаем точных начальных данных и можем описывать дальнейший её полёт только в терминах вероятностей. Как же это сделать?

Рассмотрим не одно излучение частицы и не 4 как в предыдущем случае, а допустим 3000 излучений, которые произошли в разные моменты времени и при этом допустим в разных местах (гифка 2). Наложим все эти 3 тысячи независимых событий друг на друга.

Будем рассматривать только белые - излучённые частицы, а красные отбросим. Отбрасываем красные частицы, потому, что для нас не принципиально, что послужило причиной вылета частицы. Важно только, что это некоторый случайный процесс, при этом он может быть любым. Видно, что из-за того, что изначально частицы имеют разные скорости и направления, это облако из частиц расплывается во все стороны. Такой набор из независимых событий называется статистическим ансамблем. Описать такой ансамбль можно с помощью функции плотности вероятности p(x,y,z,t), величина которой задаёт вероятность обнаружить частицу в данном элементарном объёме пространства. Функция плотности вероятности описывает случай, когда мы берём в пределе бесконечное число частиц, а не 3 тысячи как здесь. Так что распределение частиц по скоростям и координатам получается непрерывным. То есть это было бы расплывающееся белое пятно, а не облако из отдельных частиц.

Из-за того, что излучение с равной вероятностью происходит под любым углом, ансамбль получается круглый. Он имеет некоторый изначальный диаметр из-за того, что неизвестен точно момент времени излучения частицы и одни частицы уже успевают удалиться от красной частицы, а другие нет. И ансамбль расплывается из-за того, что все частицы имеют разные скорости.

При этом понятно, что частицы в таком облаке никак не взаимодействуют друг с другом. Ну и это очевидно, ведь это не настоящее облако из частиц, а это просто мы сами придумали наложить тысячи событий друг на друга и поэтому частицы здесь должны проходить просто друг сквозь друга, как показано на гифке 3.

Теперь возьмём два таких облака событий от двух излучающих атомов, расположенных один выше другого, как это показано на гифке 4.

Если два ансамбля не взаимодействующих частиц как на гифке 4 накладываются друг на друга, то в местах их наложения вероятности обнаружить частицу просто складываются, ну или можно сказать что функции плотности вероятности складываются p=p1+p2.

Вроде бы это разумно и никак не может быть иначе, но оказывается, что настоящие частицы в нашем реальном мире ведут себя иначе. В квантовой механике статистический ансамбль описывается с помощью волновых функций, которые определяют плотность вероятности обнаружения частицы в данной точке. И полётом шариков такое поведение никак не объяснишь.

На гифке 5 показано взаимодействие волновых функций настоящих фотонов. Волновые функции это конечно не сами функции плотности вероятности, так что немного некорректно вот так напрямую сравнивать гифку 4 и эту. Здесь показана амплитуда и фаза волн вероятности (яркость соответствует амплитуде, а цвет фазе), а интенсивность этих волн равна самой функции плотности вероятности. И именно интенсивность этих волн аналогична гифке 4. То есть этих зелёных и красных полос, которые показывают фазу волны, нет у функции плотности вероятности. Тем не менее, здесь явно можно видеть, что волны не проходят друг сквозь друга, никак не взаимодействуя, а они взаимодействуют - складываются, интерферируют. Шарики можно было описать скалярным полем - то есть каждой точке пространства можно сопоставить одно число - плотность вероятности обнаружить частицу в данном месте. А вот для волны в каждой точке нужно учитывать уже два числа - это амплитуду и фазу волны. При сложении двух волн амплитуды могут иметь одну и ту же фазу в данной точке и тогда они складываются, а могут иметь и противоположную фазу и тогда они вычитаются. Из-за вот этой вот возможности взаимного вычитания вероятностей образуются области, в которых вероятность обнаружить частицу равна нулю, хотя в случае классической физики такого быть не может.

2. Двухщелевой эксперимент

Рассмотрим знаменитейший двухщелевой эксперимент в случае шариков. Прохождение отдельных шариков через экран с двумя щелями показано на гифке 6.

Возьмём ансамбль из нескольких тысяч таких независимых событий (гифка 7).

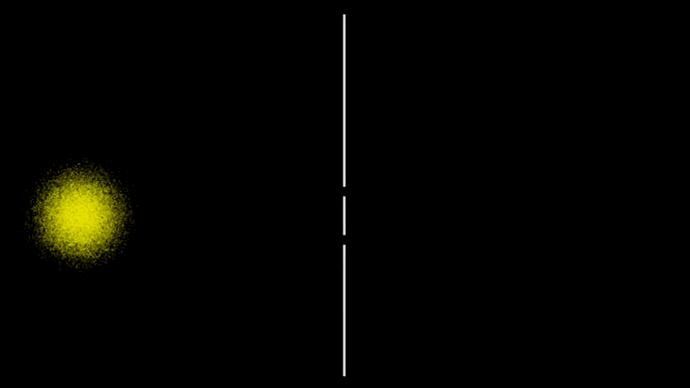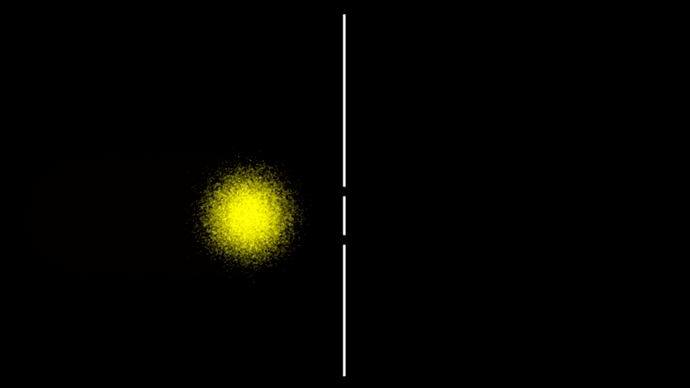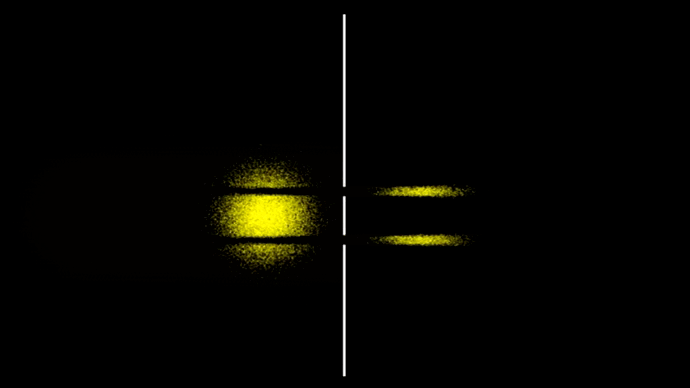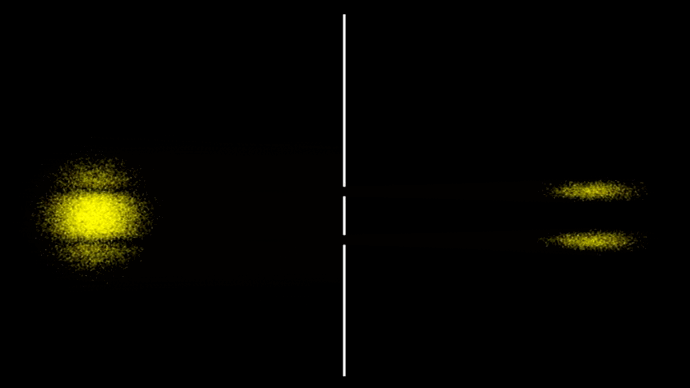
Или вот ещё тоже самое, только с белыми шариками и счётчиком числа частиц, расположенным за экраном.

Ансамбли разлетаются из-за неопределённости по скорости частиц, а там где отдельные части ансамбля пересекаются, просто накладываются друг на друга, никак не взаимодействуя друг с другом.

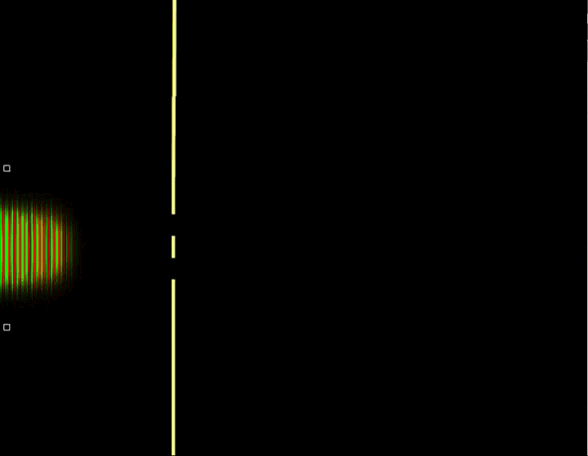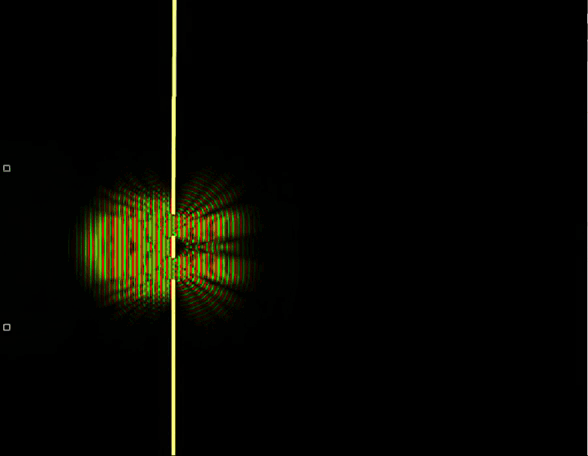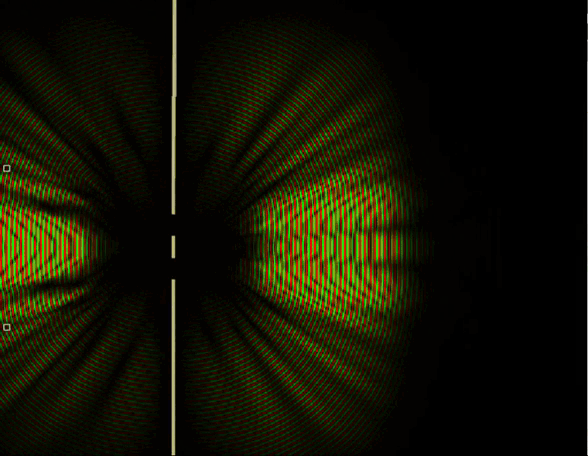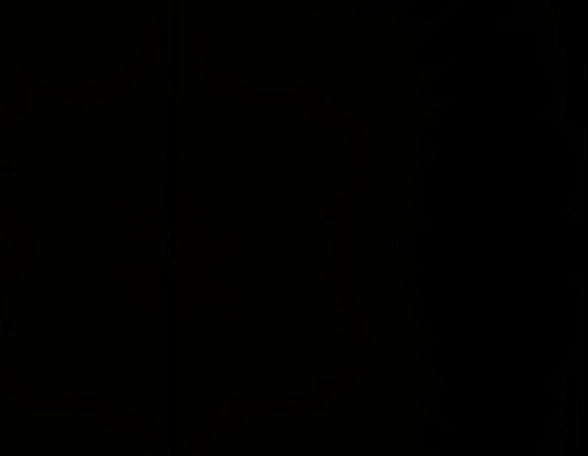
В квантовом случае волна вероятности интерферирует сама с собой и получается другая статистика. Если в предыдущем случае, когда мы рассматривали 2 атома, можно было сказать, что это просто фотоны от двух различных атомов так друг с другом взаимодействуют необычно, что получается волновое поведение, то здесь летит уже только один фотон и он может взаимодействовать только сам с собой. То есть в случае шариков мы просто сами взяли и придумали вот так вот наложить кучу событий друг на друга и назвать это статистическим ансамблем, а на самом деле полёт каждого из шариков происходит поодиночке и шарик никак не может взаимодействовать с другими шариками, так как других просто нет. А в квантовой механике получается, что альтернативные пути частиц могут взаимодействовать друг с другом. Как это ещё можно описать, кроме того, что все альтернативные пути реализуются одновременно? Причём в случае вот такого вот полёта из некоторой точки число этих альтернативных вариантов событий бесконечно, так как количество направлений вылета и число возможных скоростей бесконечно.

На гифке 10 показана уже плотность вероятности, а не сама волновая функция. То есть показан модуль волновой функции в квадрате или же интенсивность волновой функции. При возведении модуля волновой функции в квадрат информация о фазах волны исчезает, поэтому функция изображена одним цветом. Получается уже не волна, а скалярное поле – плотность вероятности.

На гифке 11 показано сравнение жёлтых частиц – шариков и плотности вероятности для, например, фотона.

При большой длине волны (гифка 12) ещё более явно проявляются волновые свойства.

Теперь предположим, что за каждой из щелей летят по электрону. Так как у электрона очень маленькая длина волны, то будем считать, что его волновой пакет (его функция плотности вероятности) имеет большое значение только около некоторой точки. То есть его можно считать точечным. При этом у фотона, проходя через щели, есть некоторая вероятность рассеяться на электронах или иначе говоря столкнуться с электронами. Столкновение фотона с электроном называется эффектом Комптона. Фотон может рассеяться либо об электрон у верхней щели, либо об электрон у нижней щели (гифка 13).

Здесь показан коллапс волновой функции с точки зрения самого электрона. То есть, при столкновении фотона с электроном, у электрона изменяется импульс и таким образом, во вселенной появляется информация о более точном положении и импульсе фотона. Как только во вселенной появляется такая информация, происходит коллапс волновой функции. Как только становится известно на каком электроне произошло рассеяние, уже бессмысленно описывать фотон как будто он идёт через две щели, уже нужно описывать его как волну, идущую от электрона на котором он рассеялся.

Но мы на самом деле в опыте не можем видеть произошло рассеяние на электроне или нет. Произошёл ли этот коллапс волновой функции с точки зрения электрона или нет. Мы только знаем, что фотон может рассеяться либо на верхнем электроне, либо на нижнем, либо вообще может не рассеяться ни на первом ни на втором и пройти через щели как будто электронов вообще не было. Для нас волновая функция электрона разделяется на 3 части - рассеявшуюся на верхнем электроне, рассеявшуюся на нижнем электроне и прошедшую через щели без рассеяния (гифка 14).

При этом, как пишет Ричард Фейнман в 8 томе Фейнмановских лекций по физике, интерференции между такими волнами уже не происходит. Мы уже должны складывать сами вероятности этих трёх альтернатив, а не волновые функции. Таким образом, чтобы это визуализировать, я просто наложил 3 волны друг поверх друга.

На этом примере видно, что коллапс волновой функции может быть субъективным. То есть с точки зрения электрона он случился сразу, а с нашей точки зрения позже, только когда наш счётчик его допустим зафиксировал уже на большом расстоянии от экрана. Поэтому коллапс волновой функции это не физический процесс в общем случае, а это получение нами информации о частице. Как например, можно подкинуть монетку, и пока не увидишь орёл там или решка, то монетка описывается вероятностями 50% на 50%, а как увидишь, то уже бессмысленно описывать вероятностями. И один человек может знать о том что выпало, а другой не знать и один будет описывать вероятностями, а другой точным значением. Другое дело, что отдельный электрон тоже может получить информацию о частице и в этом случае коллапс волновой функции можно назвать объективным - реальным, так как более элементарного наблюдателя или можно сказать получателя информации быть не может. При этом в квантовомеханических расчётах не обязательно знать, случился там коллапс волновой функции с точки зрения отдельного электрона или не случился, нужно просто знать что он в принципе может произойти. То есть, что в принципе может информация о фотоне записаться на электрон, так как это влияет на получающуюся статистику. А расчёты проводятся исходя из своей волновой функции, а не волновой функции электрона.

Из-за того, что после рассеяния на электронах волновые функции фотона, идущие от электронов не интерферируют между собой, то научные популяризаторы говорят, что они ведут себя как частицы. Но на самом деле от электронов после рассеяния идут волны вероятности, а не классические вероятности. Просто именно между собой они уже не взаимодействуют и проходят друг сквозь друга как шарики из примеров выше. А если взять саму по себе одну эту рассеянную волну, то она сама с собой будет интерферировать, если например пропустить её через ещё одну пару щелей. Так что как до коллапса волновой функции, так и после, частицу нужно описывать волновой функцией. Просто эта волновая функция при коллапсе изменяется.

Тот факт, что нам нужно знать может ли произойти запись информации на взаимодействующие частицы или не может, для правильного расчёта вероятностей, на мой взгляд указывает на то, что коллапс волновой функции, при таких взаимодействиях отдельных частиц, происходит объективно.

3. Рассеяние на круге

Теперь рассмотрим случай, когда статистический ансамбль из шариков налетает на цилиндр (гифка 15) и сравним его с квантовым случаем.

За зелёным цилиндром расположены счётчики, которые срабатывают при попадании шариков. Видно, что часть шариков отскакивает от цилиндра, а два пучка по бокам проходят без столкновения. Из-за разных скоростей шариков в пучках они расплываются и в районе счётчиков накладываются друг на друга. Это шарики, проходящие друг сквозь друга, поэтому никакого взаимодействия между пучками естественно не происходит.

Теперь посмотрим, как взаимодействует с цилиндром волновая функция (гифка 16).

Здесь хоть картина и похожая на классический случай, но при этом видна интерференция волны вероятности самой с собой, из-за чего возникают интерференционные полосы. Волновой пакет при этом также расплывается по сторонам, как и ансамбль из шариков, так как волновой пакет состоит из волн с разными длинами волн, а длина волны в квантовой механике определяет импульс, а соответственно и скорость частицы.

Здесь (гифка 17) показано взаимодействие цилиндра с частицей с большой длиной волны. Видно, что при этом рассеяние совершенно не похоже на классический случай. Это наглядно показывает то, как предсказания квантовой механики становятся неотличимыми от предсказаний классической физики при уменьшении длины волны (при увеличении частоты). Или можно сказать наоборот - чем меньше характерные размеры рассматриваемого процесса относительно длины волны, тем дальше предсказания классической механики будут отличатся от предсказаний квантовой.

Из всего вышесказанного можно сделать вывод, что квантовую частицу можно сравнить скорее не с отдельной классической частицей - точкой или шариком, а  со статистическим ансамблем из шариков. В случае классической физики мы этот ансамбль просто сами создали - выдумали, а в квантовой физике статистический ансамбль представляет собой отражение некоторой реальной сущности под названием элементарная частица, так как части этого ансамбля взаимодействуют друг с другом. Как они могли бы взаимодействовать, если бы были просто выдумкой? Так что в квантовой физике в отличие от классической нельзя отделить частицу от ансамбля и поэтому часто называют весь ансамбль частицей.

4. Орбитали

В классической физике тоже можно рассмотреть орбиталь частицы, как и в квантовой.

Если запускать по одиночке тысячи частиц на круговую орбиту, а потом наложить полёты этих частиц друг на друга, то получится ситуация как на гифке 18.

Через некоторое время сформировывается орбиталь. Она соответствует случаю, когда мы изначально не знали координату частицы, только знали, что координата находится в случайном месте в пределах некоторой окружности, а скорость частицы при этом равна орбитальной. Из-за того что орбитальная скорость зависит от расстояния до центральной частицы, то скорости получаются случайные, так как положение изначальное случайное. Таким образом, получившаяся орбиталь как и в случае квантовой физики будет говорить нам о том, какова вероятность обнаружить частицу в некотором объёме. Так что в орбитали самой по себе нет ничего исключительно квантового.

Получившаяся орбиталь похожа на кольца Сатурна, так как отдельные камешки, льдинки и пылинки практически не взаимодействуют друг с другом в кольцах, как и шарики в этой модели.

Квантовые орбитали получаются намного красивее, чем классические. Здорово, что электроны работают по квантовым законам. На гифке 20 изображена орбиталь атома водорода в возбуждённом состоянии (главное квантовое число n=7, орбитальное квантовое число L=4, магнитное квантовое число m=0). Цветом показана фаза волновой функции. Фаза постоянно меняется с течением времени, а плотность вероятности не изменяется.

Благодаря интерференции электрона с самим собой, образуется стоячая волна вот такой вот замысловатой формы. Это называется стационарным состоянием, так как с течением времени меняется только фаза волновой функции, а пространственное распределение амплитуды не меняется. Ранее говорилось, что амплитуды волн в точках с одинаковой фазой при наложении складываются. Точно также амплитуды складываются и в электромагнитной волне и в акустической допустим или в волнах на поверхности воды. То есть для фотонов амплитуды складываются как на гифках показанных ранее, но оказывается, что для электронов в атоме амплитуды в местах с одинаковой фазой не складываются, а наоборот вычитаются. Из-за того, что амплитуды у электронов не складываются, а вычитаются, два одинаковых электрона не могут быть на одной орбитали. Просто напросто две одинаковые волны гасят друг друга. Этим объясняется принцип запрета Паули, который заключается в том, что электроны в одинаковом состоянии не могут находится на одной орбитали. Но если у электронов разные спины, то интерференции между ними уже не происходит и они могут уживаться на одной орбитали. Волновые функции электронов с разными спинами не интерферируют в атоме и их вероятности уже просто складываются как в классическом случае.

Орбитали электронов в стационарном состоянии многие видели, но вот переход с одной орбитали электрона на другую, это интересный процесс.

Здесь показан переход атома водорода из основного состояния n=1 возбуждённое состояние n=2, L=1, m=0. Правда я не уверен насколько эта симуляция отражает реальный процесс поглощения фотона атомом, так как при моделировании рассматривалось взаимодействие орбитали с классическим электромагнитным полем, а не квантовым фотоном, но всё равно это интересно.

5. Туннельный эффект

Аналог туннельного эффекта также можно рассмотреть и в классической физике.

Например, если взять ансамбль из шариков, который мы рассматривали в начале статьи направить его на потенциальный барьер, то из-за того, что часть шариков имеет большую скорость в направлении движения, то эта часть скоростных шариков пробьёт препятствие, а медленные отскочат. Таким образом, потенциальный барьер отсортирует шарики по скоростям. А выглядеть это будет похоже на квантовый туннельный эффект.

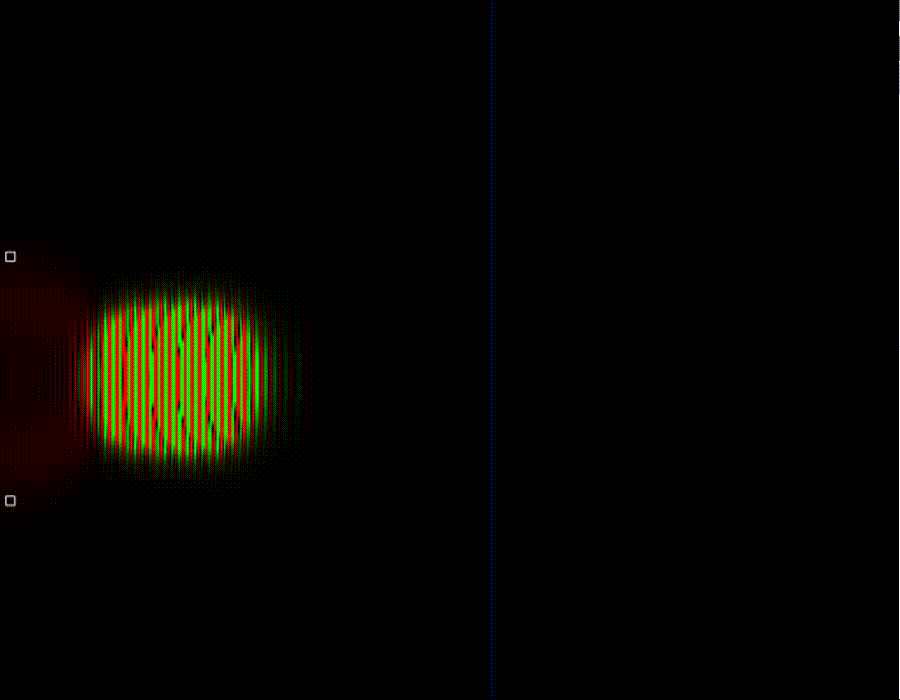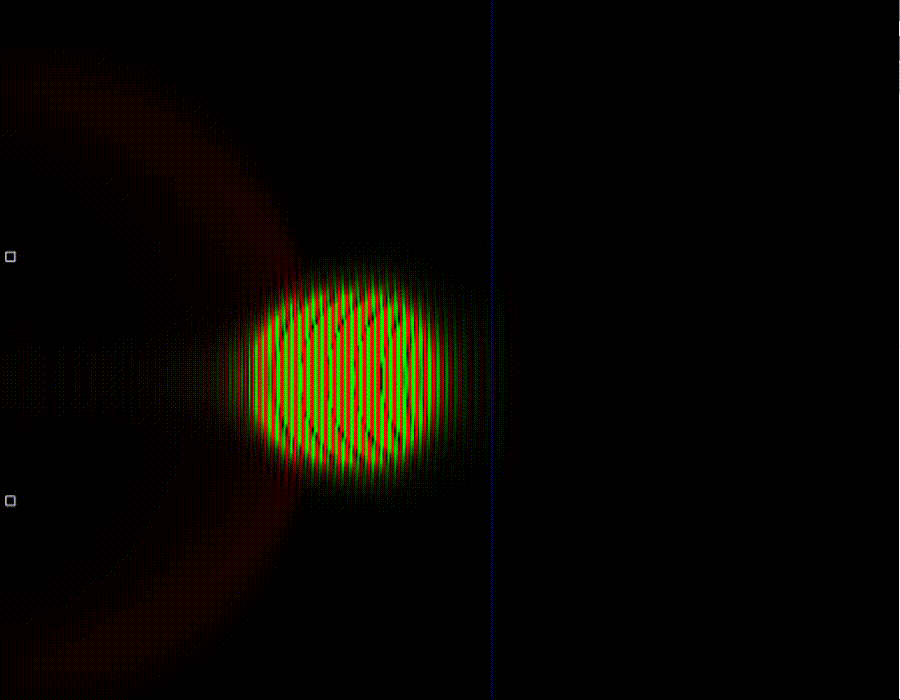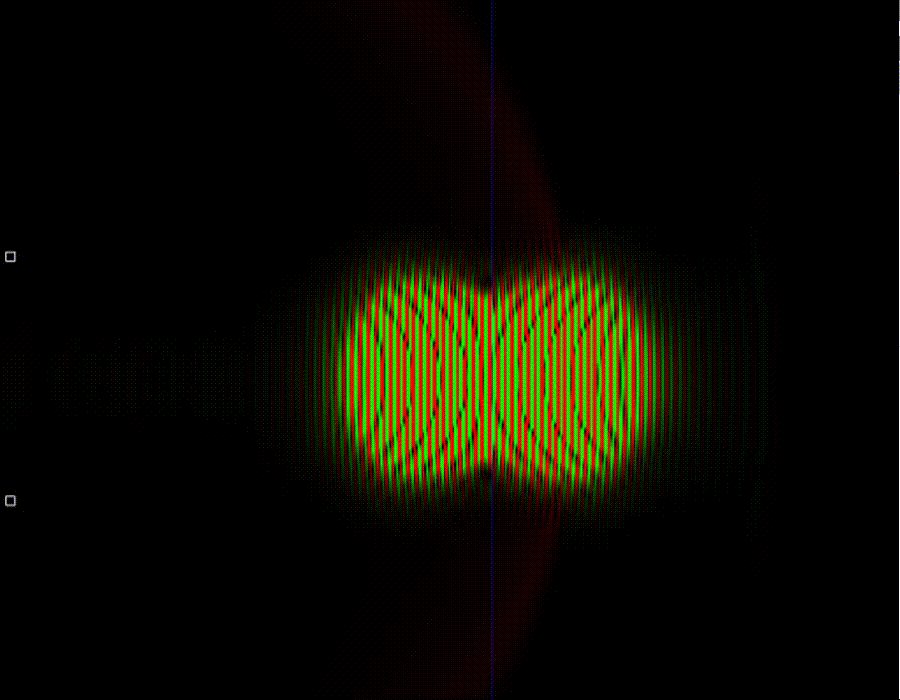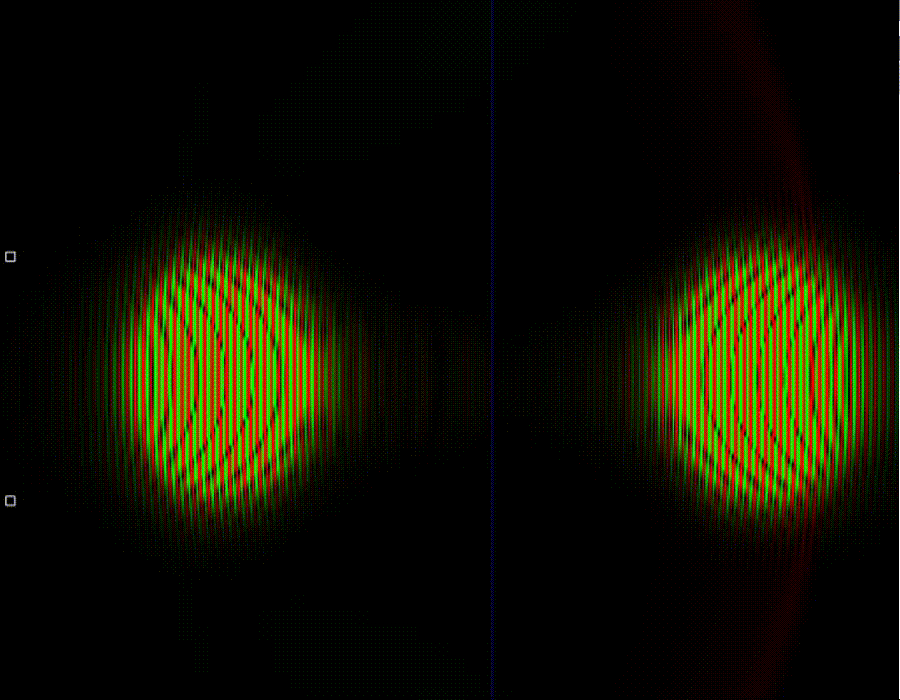
Как можно видеть, при достаточно большой частоте, то есть при большой энергии частицы квантовый туннельный эффект напоминает классический. Ключевое отличие заключается в том, что в случае квантовой статистики частицы могут преодолевать потенциальный барьер не только в случае, если у них достаточно кинетической энергии для этого, а также и в том случае если её немного не хватает. В квантовом случае частицы могут забираться в область, запрещённую классической физикой.

Когда частота волны маленькая, то процесс уже совсем не похож на классический.

6. Отражение

Также для отражения, поглощения и прохождения частиц через вещество тоже можно сделать классический аналог.

Падающий на препятствие ансамбль частиц здесь вытянут по длине. Это значит, что этот ансамбль был образован в результате какого-то случайного процесса, в котором достаточно хорошо была известна начальная скорость частицы, но не точно известен момент времени, когда частица была испущена в направлении препятствия. Поэтому из-за неизвестности по времени ансамбль вытянут.

Заметьте, что в классической механике мы можем сделать ансамбль сколь угодно маленьким, и при этом он не будет расплываться. Если процесс испускания частицы не случайный, а мы знаем и время испускания, и координату и начальную скорость, то ансамбль сойдётся в точку, и будет оставаться точкой во всех взаимодействиях. То есть просто куча частиц будет наложена друг на друга, и они будут двигаться синхронно. А вот в квантовой механике такой ансамбль, находящейся в одной точке и не расплывающийся из неё создать невозможно, так как невозможно одновременно точно задать импульс и координату. Или можно сказать, что из-за того, что волна не может быть в точке. Если задать колебание в точке, то таким образом будет создана сферическая волна, а значит такая волновая функция заданная в точке не может не расплываться. Или можно сказать, что если задать возмущение в точке, то импульс частицы будет не определён, или можно сказать, что не определена длина волны. Чтобы точно определить длину волны нужно много периодов колебаний, а у функции заданной в одной точке, нет никаких периодов.

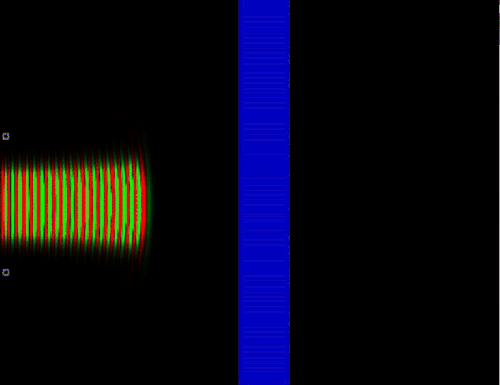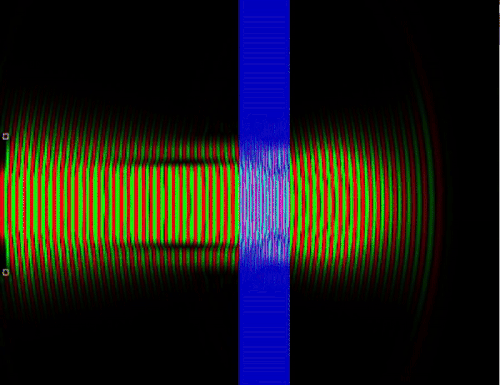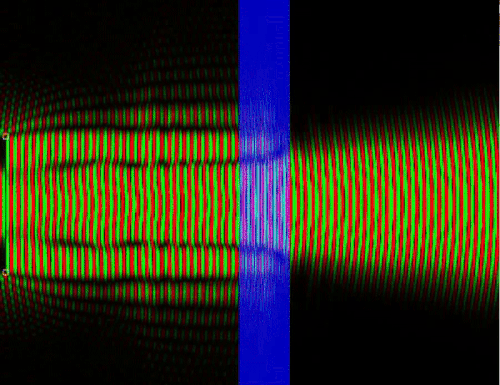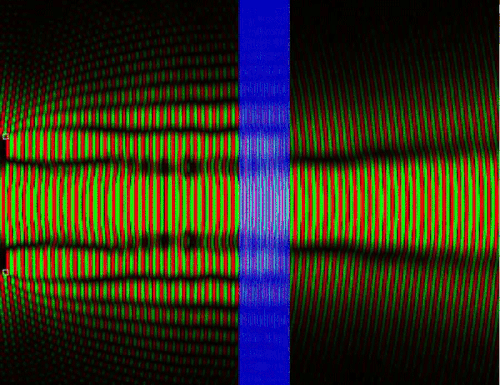
Классический случай прохождения частицы через среду не соответствует действительности, так как на самом деле волна вероятности отразившегося от, допустим, стекла фотона интерферирует с падающей волной и можно получить стоячую волну, в которой чередуются полосы максимума вероятности обнаружить частицу и минимума. Опять же, в классической физике нет интерференции ансамбля с самим собой, нет взаимодействия альтернативных сценариев развития событий.

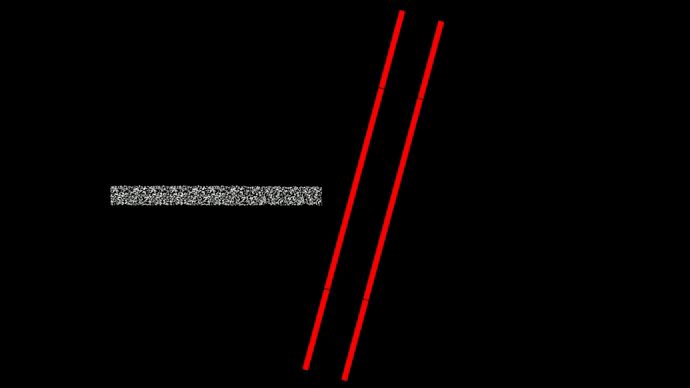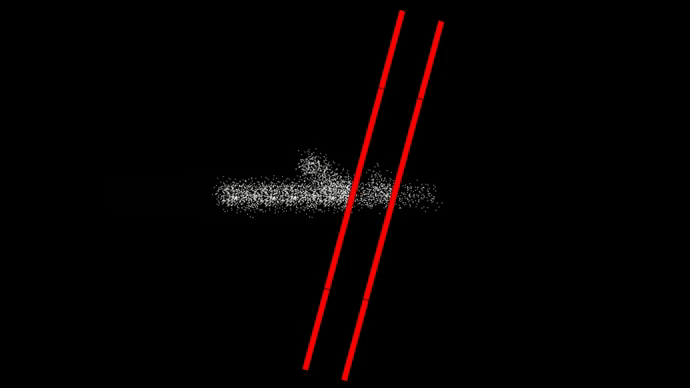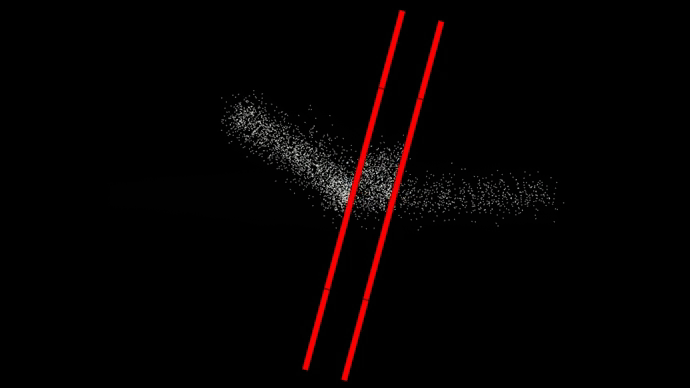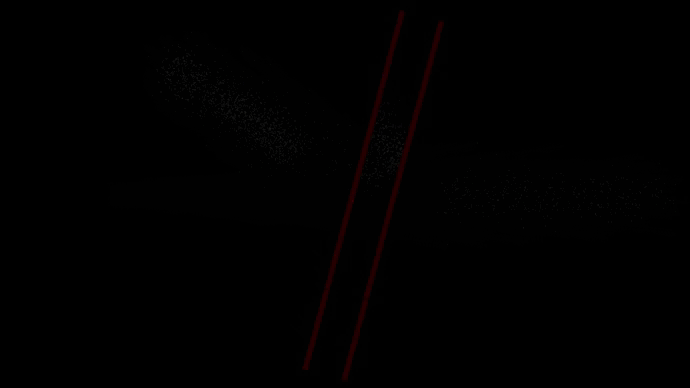
При отражении шариков от потенциального барьера угол падения равен углу отражения.

В случае с волной угол падения также равен углу отражения, но это получается в результате интерференции волновой функции, а не в результате отскока шариков. В случае с волной далеко не так очевидно на первый взгляд, что угол отражения должен быть равен углу падения. Также на симуляции можно увидеть многократное внутреннее отражение волны и её замедление в среде с коэффициентом преломления равном 2.

7. Квадратная потенциальная яма

Посмотрим, как шарики – невзаимодействующие друг с другом как призраки будут себя вести в квадратной коробке.

Ансамбль разлетается по коробке и через небольшой промежуток времени получается равномерное распределение. То есть, если бы было бесконечное число частиц, то плотность вероятности обнаружить частицу в любой точке была бы одинаковая. Здесь конечно на гифке 29. будут флуктуации в плотности вероятности из-за конечного числа частиц, но если брать достаточно большие площадки в случайных местах коробки, внутри которых подсчитывать числа шариков, то число шариков таких площадках в любом месте будет примерно одинаковое.

Квантовая частица ведёт себя в квадратной коробке совершенно по-другому. Как только края волновой функции касаются коробки и отражаются, начинается интерференция и в результате в коробке образуется стоячая волна.

8. Коллапс волновой функции

Рассмотрим интерферометр Маха-Цендера на гифке 31. Он содержит источник одиночных фотонов, который стреляет фотонами в полупрозрачное зеркало. Вероятность у фотона пройти через зеркало равна 50% и отразиться тоже 50%. Таким образом, волновая функция фотона разделяется на два волновых пакета. Затем оба волновых пакета отражаются от зеркал и направляются на второе полупрозрачное зеркало. На этом зеркале происходит интерференция двух пакетов. На выходе из зеркала волна идёт уже только вверх. Волна не идёт вниз, так как прошедшая часть верхнего пакета интерферирует с отражённой волной нижнего, а они находятся в противофазе и гасят друг друга. Разность фаз между ними можно изменять с помощью перемещения зеркала по вертикали и добиться того чтобы на выходе из зеркала было снова деление на два пакета, либо чтобы волна шла только вниз, а не вверх.

На выходе из последнего зеркала стоят два детектора - синий и красный. Для фанатов Разрушителей Легенд сделаем детекторы в виде бомб, которые могут взрываться в результате попадания одного единственного фотона. Например, можно представить, что это крайне не стабильное химическое вещество, в котором начинается цепная реакция при поглощении фотона одним единственным атомом. Причём, фотон не может отразиться от детектора, он гарантированно поглощает фотон и взрывается. При этом, волновая функция коллапсирует, так как во вселенной появляется информация о поглощении фотона. Или просто можно сказать потому, что фотон поглощается бомбой. Волновой пакет идёт только вверх, поэтому всегда будет взрываться только синяя бомба. Все 100% фотонов попадут в синий детектор. В классическом случае интерференция невозможна, поэтому вероятности попадания и в нижний и в верхний детектор были бы по 50 %.

А теперь представим, что у нас есть ещё одна белая бомба (гифка 32), которая также должна срабатывать от одного единственного фотона, при этом мы не уверены что она рабочая. Нам нужно её проверить, но при этом не взорвать. Это кажется невозможным. Как можно проверить сработает ли она от попадания одного единственного фотона или нет, если для проверки нужно запустить в неё этот самый фотон? Но оказывается, что в нашем мире, где работают законы квантовой механики это можно сделать. Это называется мысленным экспериментом Элицура-Вайдмана.

Также важная деталь - у бомбы, которую мы хотим проверить зеркальная поверхность, такая же, как и у верхнего зеркала. Так что если она не рабочая, то ситуация неотличима от той, когда вместо бомбы обычное зеркало (гифка 31). Если бомба не рабочая, то будет наблюдаться интерференция на выходном полупрозрачном зеркале и вероятность фотона попасть в красный детектор будет нулевая, а в синий 100%. Но теперь предположим, что бомба всё таки рабочая, как на гифках 32-34. Тогда нижний волновой пакет будет поглощаться бомбой (гифка 32).  Заметьте, что поглощение волнового пакета это не поглощение самого фотона, или в данном случае можно было бы сказать "половины фотона". Сам фотон не делим, а волновой пакет задаёт только распределение вероятности, но не является самим фотоном. Происходит поглощение именно этой вероятности можно сказать. Таким образом, рабочая бомба в 50 % случаев взорвётся, так как на первом делителе вероятность делиться пополам, как показано на гифке 32. При взрыве бомбы волновая функция коллапсирует и вероятность обнаружить фотон на синем или красном детекторе становится равной нулю. Понятное дело, что если ты знаешь, что фотон поглотился, то описывать его так, как будто он ещё имеет вероятность полететь дальше не правильно.

При этом очень интересно, что для бомбы волновая функция коллапсирует сразу же, как только фотон в неё попадает (волна пропадает на гифке 32 после взрыва бомбы). А вот с точки зрения синего и красного детекторов, которые находятся, допустим, на очень большом расстоянии (можно, например, сделать гигантский интерферометр длиной в световой год), коллапса волновой функции ещё не произошло. До детекторов ещё не дошла информация о том, что бомба взорвалась. Они об этом ничего не знают, и по-прежнему с их точки зрения верхний волновой пакет летит к детекторам и поэтому фотон имеет 50 % вероятность дойти до одного из двух детекторов. Только когда уже проходит много времени, а срабатывания ни одного из детекторов не происходит, то волновая функция коллапсирует и с точки зрения детекторов тоже. Умные детекторы понимают, что если до них фотон не дошёл, то значит, что бомба взорвалась.

Но рассмотрим случай, когда бомба рабочая, но при этом не взорвалась. Так как бомба рабочая, то происходит поглощение нижнего волнового пакета. Дальше летит только верхний и на полупрозрачном зеркале разделяется на два. Верхний волновой пакет представляет собой вероятность 50%, поэтому после его разделения на 2 части (гифка 33,34) получается, что вероятность срабатывания синего и красного детекторов равна по 25 %.

Если взрывается синий детектор, то неизвестно рабочая была белая бомба или нет, так как в случае не рабочей белой бомбы, когда она просто отражала как зеркало, все фотоны летели как раз именно в синий детектор, как и в случае с рабочей белой бомбой, а вот если взрывается красный детектор, то становится понятно, что белая бомба рабочая. Таким образом, при срабатывании красного детектора в 25% случаев, можно узнать, что белая бомба рабочая и при этом не взорвать её. То есть, как бы фотон летит одновременно во множестве параллельных миров, реализует все возможные сценарии, виртуально взаимодействует с бомбой и поэтому мы можем извлечь информацию из фотона о том, как он там взаимодействовал и с чем в параллельных альтернативах своих судеб.