6.4 Устойчивость систем автоматического регулирования. Частотный критерий устойчивости Михайлова / forpes.ru

Главная
6.4 Устойчивость систем автоматического регулирования. Частотный критерий устойчивости Михайлова

6.4 Устойчивость систем автоматического регулирования. Частотный критерий устойчивости Михайлова +17

05.04.2023 21:09

petuhoff 5 2100 Источник

1. Введение в теорию автоматического управления.2. Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13.

3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕГУЛИРОВАНИЯ. 3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ. 3.2. Типовые звенья систем автоматического управления регулирования. Классификация типовых звеньев. Простейшие типовые звенья. 3.3. Апериодическое звено 1–го порядка инерционное звено. На примере входной камеры ядерного реактора. 3.4. Апериодическое звено 2-го порядка. 3.5. Колебательное звено. 3.6. Инерционно-дифференцирующее звено. 3.7. Форсирующее звено. 3.8. Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9. Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности.

4. Структурные преобразования систем автоматического регулирования.

5. Передаточные функции и уравнения динамики замкнутых систем автоматического регулирования (САР).

6. Устойчивость систем автоматического регулирования. 6.1 Понятие об устойчивости САР. Теорема Ляпунова. 6.2 Необходимые условия устойчивости линейных и линеаризованных САР. 6.3 Алгебраический критерий устойчивости Гурвица.

6.4. Частотный критерий устойчивости Михайлова

Советским ученым Михайловым в 30-тых годах впервые был предложен оригинальный критерий оценки устойчивости САР, основанный на исследовании частотных свойств полинома при подстановки вместо $s=i\cdot \omega$ , где $\omega \in [0, \infty [;$

Связь между частотными свойствами системы и передаточными функцииями более подробно описана в лекции 3. Частотные характеристики САР

$D(s)=a_0\cdot s^n+a_1 \cdot s^{n-1}+ \cdots +a_{n-1}\cdot s+ a_n \ \ \ \ \ \ \ \ \mathbf{(6.4.1)}$

Подставим $s = i \cdot \omega$ в формулу 6.4.1 $\Rightarrow$

$D(i\cdot \omega)=D_1(\omega)+i\cdot D_2(\omega) \ \ \ \Rightarrow \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(6.4.2)}$ $\Rightarrow \begin{cases} D_1(\omega) =a_n-a_{n-2}\cdot \omega^2+a_{n-4}\cdot \omega^4- ... \\ D_2(\omega) = -a_{n-3}\cdot \omega^3+a_{n-5}\cdot\omega^5-\cdots \end{cases} \ \ \ \ \ \ \ \ \mathbf{(6.4.3)}$

Совершенно очевидно, что:

$\text{если }\omega \rightarrow 0 \Rightarrow \begin{cases} D_1 \rightarrow a_n \\D_2 \rightarrow 0 \end{cases}$ $\text{если }\omega \rightarrow 0 \Rightarrow \begin{cases} D_1 \rightarrow \pm\infty \\D_2 \rightarrow \pm\infty \end{cases}$

Критерий устойчивости Михайлова:

Чтобы САР (замкнутая или разомкнутая) была устойчивой, необходимо и достаточно, чтобы годограф $D(i\cdot\omega)$ при изменении $\omega$ от нуля до $\infty$ переходил поочередно из квадранта в квадрант против часовой стрелки, совершив при этом поворот на угол $\frac{\pi}{2}\cdot n$ , где - степень полинома .

На рисунке 6.4.1 представлены варианты годографов для различных степеней n полинома

Рисунок 6.4.1 Годографы устойчивых систем

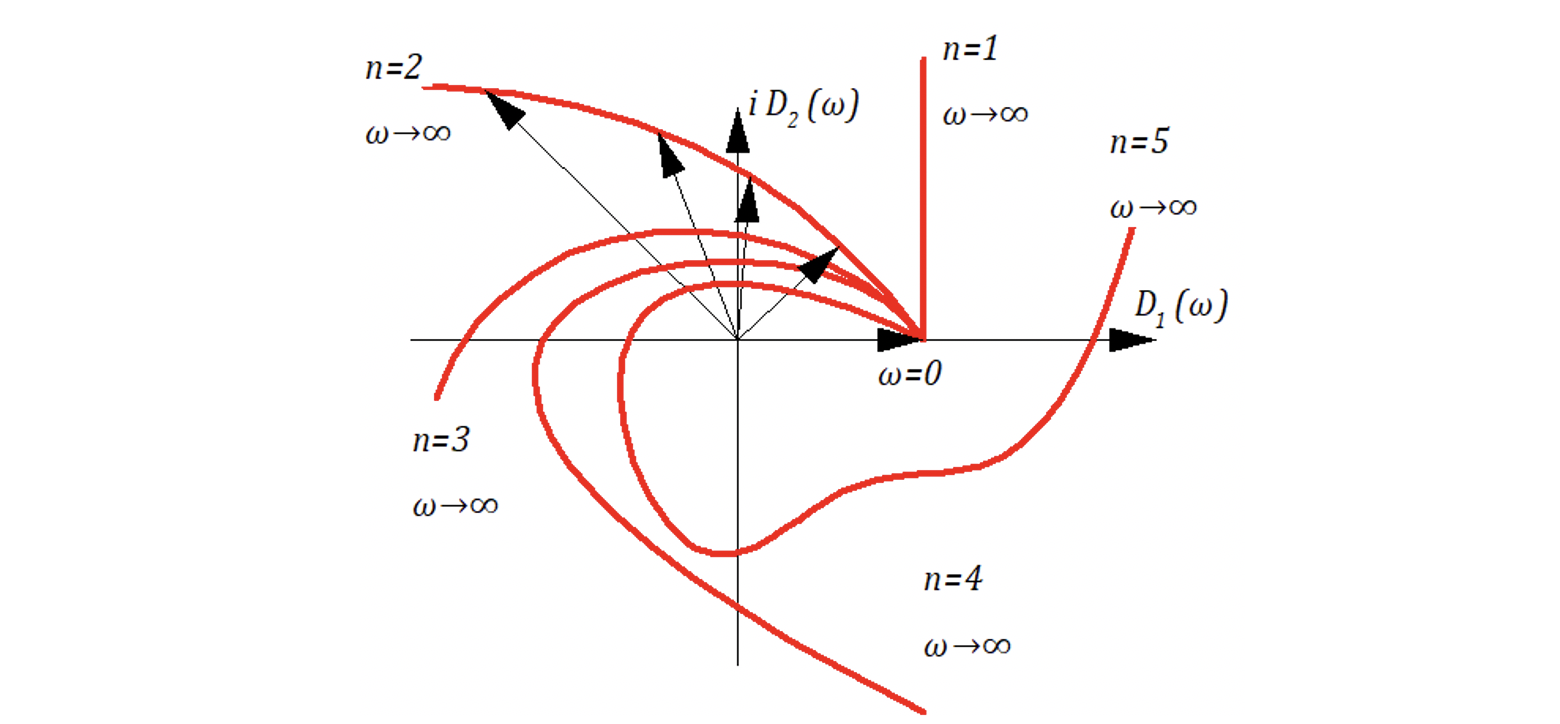
Если САР устойчива, то вектор $D(i\cdot\omega)$ при изменении $\omega$ от 0 до $\infty$ совершает поворот на угол $\frac{\pi}{2}\cdot n$ , где n - степень полинома .

Следствием частотного критерия Михайлова является перемежаемость (чередование) нулей полиномов $D_1(\omega)$ и $D_2(\omega)$ в самом деле (см. рисунок 6.4.1), для кривой с последовательность пресечения осей получается как на рисунке 6.4.2

Рисунок 6.4.2. Нули полиномови чередуются для устойчивости системы. — Рисунок 6.4.2. Нули полиномов $D_1(\omega)$ и $D_2(\omega)$ чередуются для устойчивости системы.

Если система находится на апериодической границе устойчивости (один нулевой полюс при всех остальных в левой полуплоскости), то годограф $D_1(i\cdot \omega)$ имеет следующий «примерный» вид, см. рисунок 6.4.3:

Рисунок 6.4.3 - Годограф начинается из начала координат и поочередно «проходит» все квадранты в положительном направлении (начиная со 2-го квадранта).

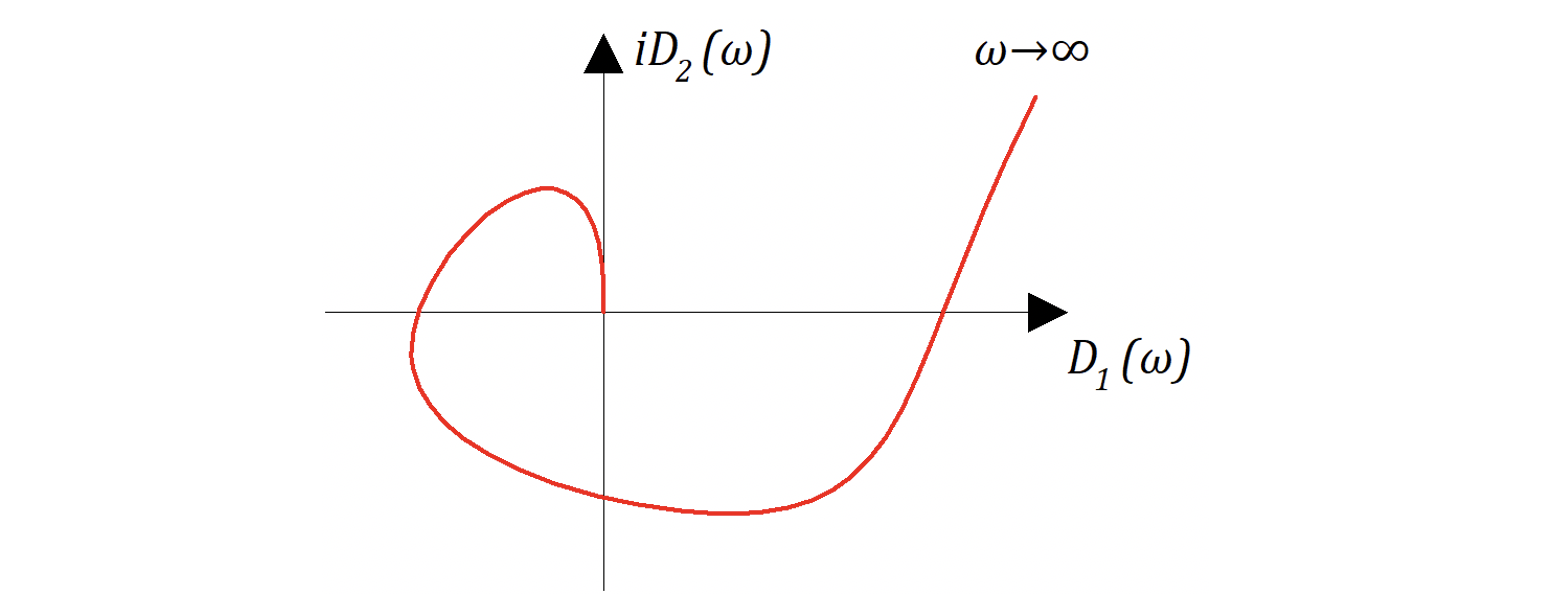
Если система находится на колебательной границе устойчивости (2 чисто мнимых полюса при всех остальных в левой полуплоскости), то годограф имеет вид как на рис. 6.4.4:

Рисунок 6.4.4 - Годограф при некоторой частоте проходит через начало координат, «перескакивая» из 2-го в 4-ый квадрант (минуя 3-ий). Частота - частота незатухающих колебаний в такой САР. — Рисунок 6.4.4 - Годограф $D(i\cdot\omega)$ при некоторой частоте $\omega = \omega^*$ проходит через начало координат, «перескакивая» из 2-го в 4-ый квадрант (минуя 3-ий). Частота $\omega^*$ - частота незатухающих колебаний в такой САР.

Если САР неустойчива, годографы имеют вид как представлено на рисунке 6.4.5:

Рисунок 6.4.5. Годографы неустойчивых систем.

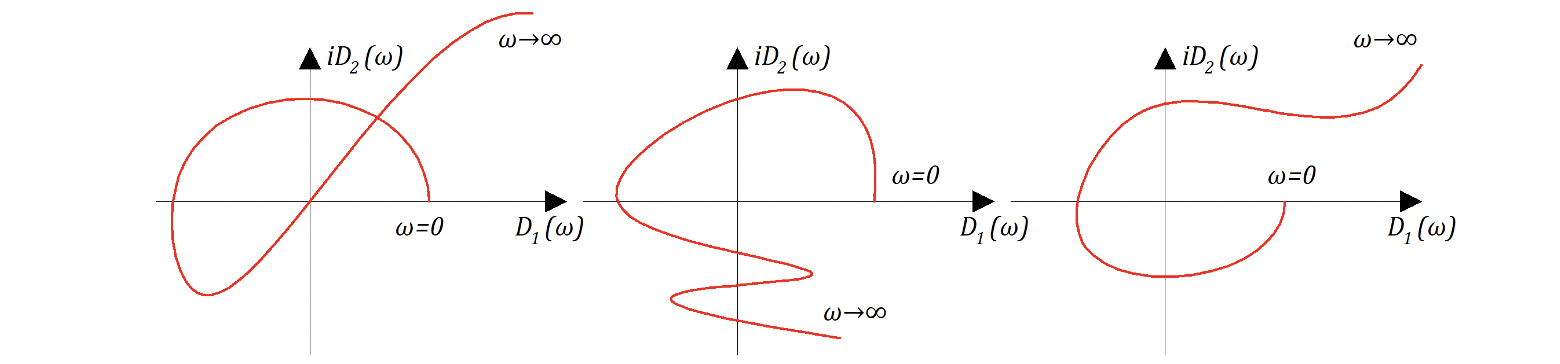
Докажем ряд основных моментов в критерии Михайлова.

Представим полином в виде произведения:

$D(s)=a_0\cdot(s-s_1)\cdot(s-s_2)\cdot...\cdot(s-s_n) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(6.4.3)}$

где - полюса главной передаточной функции.

Учитывая, что любое комплексное число типа $(a+i\cdot b)$ можно представить в виде: $(a+i\cdot b)=A\cdot e^{i\cdot \varphi},$ где – модуль, $\varphi$ - фаза. $\Rightarrow$

$D(i\cdot \omega)=a_0\cdot(i\cdot\omega-s_1)\cdot(i\cdot\omega-s_2)\cdot...\cdot(i\cdot\omega-s_n) =\\=a_0\cdot A_1(\omega)\cdot e^{i\cdot\varphi_1(\omega)}\cdot A_2(\omega)\cdot e^{i\cdot\varphi_2(\omega)}\cdot...\cdot A_n(\omega)\cdot e^{i\cdot\varphi_n(\omega)}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(6.4.4)}$

Рассмотрим изменнение фазы, при изменении $\omega$ от 0 до $\infty$ . Обозначим изменение фазы как $\Delta \varphi(\omega)$

$\Delta\varphi|_{\omega=0}^{\omega=\infty}=\Delta arg(i\cdot \omega-s_j)|_{\omega=0}^{\omega=\infty}=\Delta arg(i\omega-s_j) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(6.4.5)}$

Для устойчивой САР, все полюса D(s) лежат в левой полуплоскости. (см. предыдущию лекцию) Рассмотрим различные варианты расположения полюсов на плоскости:

1-й случай: пусть является реальным числом $s_j \in R$ , например, $s_j=-\alpha_1$ , где $\alpha_1 >0$ , поскольку корень в левой полуплоскости.

Рассмотрим поведение вектора $(i\omega-s_j)$ при изменении от нуля до бесконечности $\Rightarrow (i\omega-s_j)=(i\omega+\alpha_1)=\alpha_1+i\omega$

Рисунок 6.4.6. Вектор для реального корня — Рисунок 6.4.6. Вектор $i\omega+\alpha_1$ для реального корня

Из рисунка 6.4.6 очевидно, что $0<\omega_1<\omega_2<\omega_\infty$

при $\omega=0 \Rightarrow\varphi_1(0)=0$ ,

при $\omega\rightarrow\infty \Rightarrow\varphi_1(\infty)\rightarrow\frac{\pi}{2}$ .

$\Delta\varphi|_{\omega=0}^{\omega=\infty}=\Delta arg(i\cdot \omega+s_j)=\Delta arg(\alpha_1+i\omega)=\frac{\pi}{2} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(6.4.6)}$

Т.е. при изменении $\omega$ от 0 до $\infty$ вектор, описывающий скобку $(i\omega-s_1)$ повернется в положительном направлении на угол $\frac{\pi}{2}$ .

2-й случай: Пусть $s_2=-\alpha_2+i\cdot\beta_2$ где, $\alpha_2>0; \beta_2>0$ преобразуем скобку: $(i\omega-s_1)\Rightarrow$

$(i\omega-s_2)=(i\omega+\alpha_2-i \beta_2)=[\alpha_2+i\cdot(\omega-\beta_2)]$

Рассмотрим изменение $\omega$ от до $\infty$ :

при $\omega=0\Rightarrow (i\omega-s_2)=[\alpha_2-i\beta_2]$ - точка лежит в правом нижнем квадранте коплексной плоскости, фаза (сдвиг фазы):

$\varphi_2 (0)= \gamma_2=arctg(\frac{\alpha_2}{\beta_2})$ (см. рис. 6.4.7)

при $\omega \rightarrow \infty$ фаза (сдвиг фазы) $\varphi_2(\infty)\rightarrow \frac{\pi}{2}$ (см. рис. 6.4.7)

Рисунок 6.4.7 Вектор длядля комплексного корня. — Рисунок 6.4.7 Вектор для $\alpha_2+i\cdot(\omega-\beta_2)$ для комплексного корня.

Рисунок 6.4.7 Вектор для $\alpha_2+i\cdot(\omega-\beta_2)$ для комплексного корня.

Изменение фазы:

$\Delta arg(i\omega-s_2)=\frac{\pi}{2}+\gamma_2 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(6.4.7)}$

3-й случай: Пусть $s_3=-\alpha_2-i\cdot\beta_2$ (полюс комплексно сопряженный со вторым вариантом). Преобразуем скобку $(i\omega-s_3)\Rightarrow$

$(i\omega-s_3)=(i\omega+\alpha_2+i\cdot\beta_2)=[\alpha_2+i\cdot(\omega+\beta_2)]$

Рассмотрим изменение $\omega$ от до $\infty$ :

при $\omega=0\Rightarrow (i\omega-s_3)=[\alpha_2+i\beta_2]$ - точка лежит в правом верхнем квадранте коплексной плоскости, фаза (сдвиг фазы):

$\varphi_2 (0)= -\gamma_2=-arctg(\frac{\alpha_2}{\beta_2})$ (см. рис. 6.4.8)

при $\omega \rightarrow \infty$ фаза (сдвиг фазы) $\varphi_2(\infty)\rightarrow \frac{\pi}{2}$ (см. рис. 6.4.8)

Рисунок 6.4.8 Вектор длядля комплексного корня. — Рисунок 6.4.8 Вектор для $\alpha_2+i\cdot(\omega+\beta_2)$ для комплексного корня.

Изменение фазы:

$\Delta arg(i\omega-s_3)=\frac{\pi}{2}-\gamma_2 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(6.4.8)}$

Рассмотрим изменения годографа полинома устойчивой системы c учетом изменения фазы для трех случаев полюсов рассмотрены выше.

Пусть у нас общее количество полюсов , - количество сопряженных полюсов полинома, тогда количество вещественных полюсов.

$\Delta arg D(i\cdot\omega)|_{\omega=0}^{\omega=\infty}=\sum^n_{j=1}\varphi_j=\sum_{j=0}^n\Delta arg(i\omega-s_j) =\\=k\cdot(\frac{\pi}{2}+\gamma_j+\frac{\pi}{2}-\gamma_j)+(n-k)\cdot \frac{\pi}{2} = n\cdot\frac{\pi}{2}$

Покольку вещественны полюс дает $\Delta arg(i\omega-s_j)=\frac{\pi}{2}$ (cм. формулу 6.4.6), а два комплексно сопряженных корня в сумеее дают $2\cdot\frac{\pi}{2}$ (формулы 6.4.7 и 6.4.8) $\Rightarrow$

$\Delta argD(i\omega)=n\cdot\frac{\pi}{2}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(6.4.9)}$

Это означает, что при изменении частоты от нуля до бесконечности, годограф $\mathbf{D(i\cdot\omega)}$ должен поочередно пройти все квадранты в положительном направлении, если САР – устойчива.

Рассмотрим неустойчивую САР, у которой ряд полюсов полинома расположен в правой полуплоскости.

4-й случай: Пусть $s_4=\alpha_4;$ где $\alpha_4>0$ - реальное число.

Преобразуем скобку подставля значения полюса $(i\omega-s_j)$ $\Rightarrow (i\omega-s_j)=(i\omega+\alpha_4)=-\alpha_4+i\omega$ .

Рассмотрим изменние вектора $(-\alpha_4+i\cdot\omega)$ при изменении $\omega$ от 0 до $\infty$ . Примерный вид представлен на рисунке 6.4.9, где $\omega_0<\omega_1<\omega_2$ :

Рисунок 6.4.9 Вектор длядля комплексного корня. — Рисунок 6.4.9 Вектор для $-\alpha_4+i\cdot\omega$ для комплексного корня.

Изменение фазы вектора:

при $\omega =0 \Rightarrow \varphi_4(0)=\pi$ ;

при $\omega\rightarrow\infty\Rightarrow \varphi_4(\omega_\infty)\rightarrow\frac{\pi}{2}$ .

Изменение фазы:

$\Delta arg(i\omega-s_4) =-\frac{\pi}{2} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(6.4.10)}$

Следовательно отрицательный реальный полюс дает вращение вектора $D(i\omega)$ в отрицательном направлении на угол $-\frac{\pi}{2}$ . Получается наличе одного реального полюса вызывает "недоповорот" вектора $D(i\omega)$ на угол $\pi$ .

Рассмотрим два варианта с коплексными полюсами лежашими в левой полуплоскости:

5-й случай: Пусть $s_5=\alpha_5+i\cdot \beta_5$ , где $\alpha_5>0$ и $\beta_5>0$ преобразуем скобку $(i\omega-s_5)$ для данного случая:
$(i\omega-s_5)=i\omega-\alpha_5-i\cdot \beta_5=-\alpha_5+i(\omega-\beta_5)$ .

Рассмотрим изменние вектора $-\alpha_5+i(\omega-\beta_5)$ при изменении $\omega$ от 0 до $\infty$ . Примерный вид представлен на рисунке 6.4.10, где: $\omega_1<\omega_2<\omega_3$ , $\gamma_5 = arctg\left(\frac{\beta_5}{\alpha_5}\right)$

Рисунок 6.4.10 Вектор длядля комплексного корня. — Рисунок 6.4.10 Вектор для $-\alpha_5+i\cdot(\omega-\beta_5)$ для комплексного корня.

Рисунок 6.4.10 Вектор для $-\alpha_5+i\cdot(\omega-\beta_5)$ для комплексного корня. Изменение фазы вектора:

при $\omega =0 \Rightarrow \varphi_5(0)=\pi+\gamma_5$ ;

при $\omega\rightarrow\infty\Rightarrow \varphi_5(\omega_\infty)\rightarrow\frac{\pi}{2}$ .

Изменение фазы:

$\Delta arg(i\omega-s_5)=-\frac{\pi}{2}-\gamma_5 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(6.4.11)}$

6-й случай: Пусть $s_6=\alpha_5-i\cdot \beta_5$ , явялется комплексно сопряженным полюсом для 5-го случая, где $\alpha_5>0$ и $\beta_5>0$ преобразуем скобку $(i\omega-s_j)$ для данного случая: $(i\omega-s_6)=(i\omega-\alpha_5+i\cdot\beta_5)=-\alpha_5+i\cdot(\omega+\beta_5)$ .

Рассмотрим изменние вектора $-\alpha_5+i(\omega+\beta_5)$ при изменении $\omega$ от 0 до $\infty$ . Примерный вид представлен на рисунке 6.4.11, где: $\omega_1<\omega_2<\omega_3$ , $\gamma_5 = arctg\left(\frac{\beta_5}{\alpha_5}\right)$

Рисунок 6.4.11 Вектор длядля комплексного корня. — Рисунок 6.4.11 Вектор для $-\alpha_5+i\cdot(\omega+\beta_5)$ для комплексного корня.

при $\omega =0 \Rightarrow \varphi_6(0)=\pi-\gamma_5$ ;

при $\omega\rightarrow\infty\Rightarrow \varphi_6(\omega_\infty)\rightarrow-\frac{\pi}{2}$ .

Изменение фазы:

$\Delta arg(i\omega-s_6)=-\frac{\pi}{2}+\gamma_5 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(6.4.12)}$

При наличии двух комплексно-сопряженных корней в левой полуплоскости (варианты 5 и 6) общее изменение фазы вычисляется по формуле:

$\sum_{j=5}^{j=6} \Delta arg(i\omega-s_6)=-\frac{\pi}{2}-\gamma_5-\frac{\pi}{2}+\gamma_5=-\pi$

Резюмируем:

Если САР - устойчива все полюса полинома степенью лежат в левой полуплоскости, то изменение фазы годографа $D(i\cdot\omega)$ при изменении $\omega$ on 0 до $\infty$ описывается формулой 6.4.13:

$\Delta arg D(i\cdot \omega)=n\cdot\frac{\pi}{2}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(6.4.13)}$

Если один полюс полинома степенью лежит в правой полуплоскости, а остальные в левой полуплоскости, то изменение фазы годографа $D(i\cdot\omega)$ при изменении $\omega$ on 0 до $\infty$ описывается формулой 6.4.14:

$\Delta arg D(i\cdot \omega)=n\cdot\frac{\pi}{2}- \pi \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(6.4.14)}$

Если в правой полуплоскости расположено L полюсов полинома степенью , а остальные в левой полуплоскости, то изменение фазы годографа $D(i\cdot\omega)$ при изменении $\omega$ on 0 до $\infty$ описывается формулой 6.4.15:

$\Delta arg D(i\cdot \omega)=n\cdot\frac{\pi}{2}-L\cdot \pi \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(6.4.15)}$

Предельный случай

Если один из полюсов полинома явялется бесконечным (см. рисунок 6.4.12):

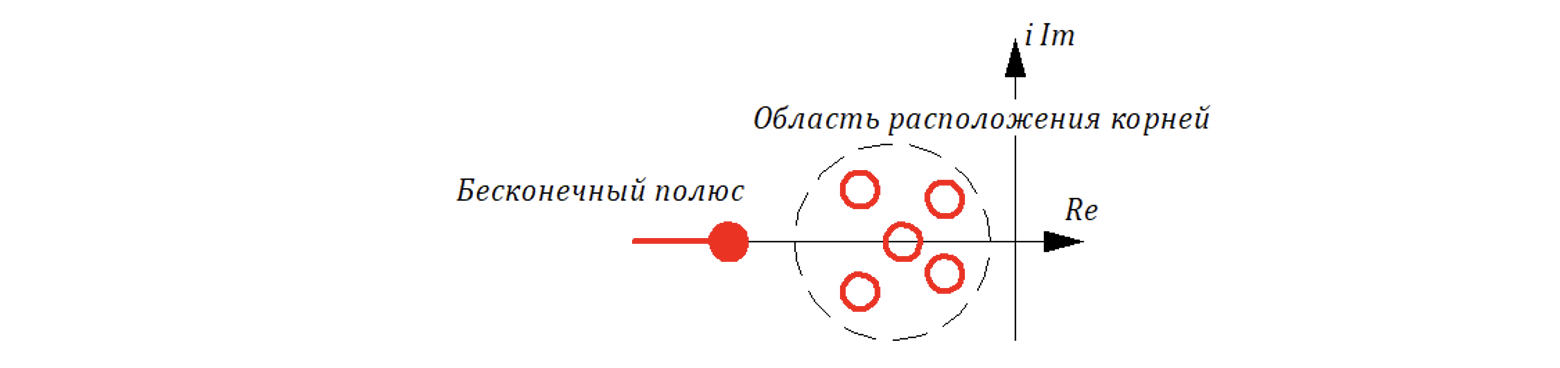
Данный случай возникает, если $a_0\rightarrow0$ годограф $D(i\cdot\omega)$ в этом случае ведет себя как показано на рисунке 6.4.13:

Рисунок 6.4.13 Вид годографа c "бесконечным" корнями — Рисунок 6.4.13 Вид годографа $D(i\cdot\omega)$ c "бесконечным" корнями

Пример

Исследовать на устойчивость САР , представленную на рисунке 6.4.14 с использованием критерия Михайлова

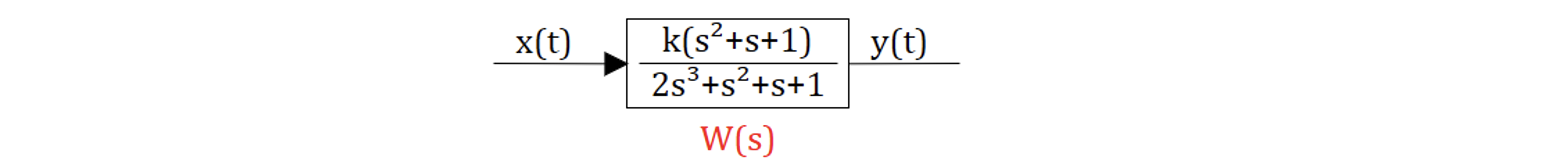
Полином $D(s)=2\cdot s^3+s^2+s+1$ $\Rightarrow$ $D(i\cdot\omega)=-2\cdot i\cdot \omega^3-\omega^2+i\cdot \omega+1$

$\begin{cases} D_1(\omega)=1-\omega^2; \\ D_2(\omega)=\omega-2\cdot\omega^3.\end{cases}$

Корни полинома $D_1(\omega)$ : $\omega_{1.1} =1$ ;

Корни полинома $D_2(\omega):$ $\omega_{2.1} =0,\ \omega_{2.2}=\frac{\sqrt{2}}{2}$ ;

Чередования 0 для полиномов $D_1,\ D_2$ не происходит, (см. рис. 6.4.15)

Определим какие должны быть коэффициенты полинома и что бы САР была устойчивой согласно критерию Михайлов.

Для устойчивой системы, необходимо чередование корней, для нашего случа корни могут распологаться по возрастанию в следующем порядке: $\omega_{2.1}<\omega_{1.1}<\omega_{2.2};$

Изменим коэффициент так, что-бы неравенство $\omega_{2.2}>(\omega_{1.1}=1)$ сталов верным. Например пусть $\omega_{2.2}=2$ . Тогда решая уравнение для $D_2(\omega)=\omega -x\cdot \omega^3 =0$ , при $\omega=2$ получаем коэффициент $\Rightarrow$

$D(i\cdot\omega)=D_1(i\cdot\omega)+D_2(i\cdot\omega)=1 +(\omega\cdot i)^2+\omega\cdot i+0,25\cdot(\omega\cdot i)^3\Rightarrow$ $D(s)=0.25\cdot s^3+s^2+s+1$

Проверим результат численным моделированием. Создадим стуркутурную схему, как показанао на рисунке 6.4.15.

Рисунок 6.4.15 Схема модели для проверки решения примера 1.

Используем блок передаточная переменная общего вида, где будем задавать, коэффициет k, из условия задачи в качестве глобальной переменной, меня которую можно изменять коэффициент числителя (см. рис. 6.4.15). Зададим в качестве тестового воздействия ступеньку на 5-й секунду, так же поместим на схему блок построения гадогрофа Михайлова. Результаты расчет приведены на рисунке 6.4.16

Рисунок 6.4.16 Расчет неустойчивой системы.

Меняя коэффициет , можно убедиться, что система остается неустойчивой, при любых значениях коэффициента меняется только амплитуда колебательного процесса. График годографа Михайлова показывает, что годограф $D(i\cdot\omega)$ переходит из квадранта в квандрат комплексной полсокости, по часовой стрелке (см. рис. 6.4.16).

Изменим коэффициент блока предаточной функции общего вида рассчитанные для получения чердования корней $D(s)=0.25\cdot s^3+s^2+s+1$ , и повторим расчет. Изменненная модель и результаты моделирования представлены нар рисунке 6.4.17

Рисунок 6.4.17 Расчет устойчивой системы.

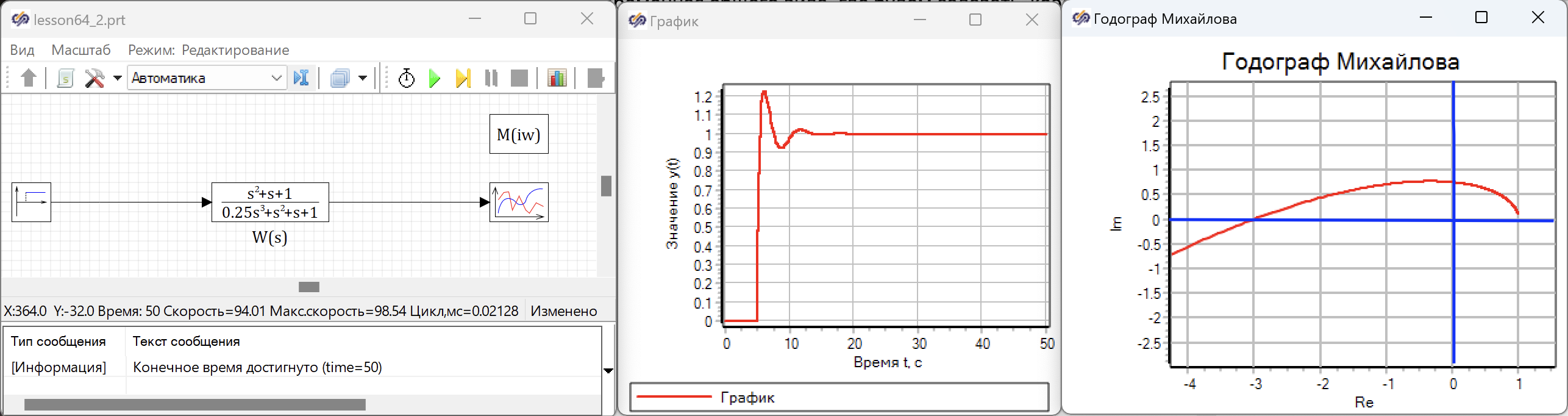
Измененная система, оказывается устойчивой. При единичном ступенчатом воздействии она приходит в новое состояние равновесия. Точно так же, как для неустойчивой системы, для устойчивой системы коэффицент влияет только на амплитуду выхода, но не влияет на устойчивость. Для устойчиваой системы график годографа Михайлова показывает, что годограф $D(i\cdot\omega)$ переходит из квадранта в квандрат комплексной полсокости, против часовой стрелке (см. рис. 6.4.17).

Далее будет совсем жестко - годограф Найквиста! Не переключайтесь!

Комментарии (5)

Nikeware
06.04.2023 09:02
#25414856
+1
Совершенно очевидно, что:

Формула (6.4.3). Что-то там совершенно не очевидно :-(
при w->0 : D2 к an-1
при w->inf (у Вас опечатка): D2 к +/-inf

Или я что-то не так вижу?
1. petuhoff Автор
  06.04.2023 09:02
  #25415676
  Да это ошибка! у D2 же нет свободного члена, там собранны все слогаемые с i, а и может быть только в паре с $\omega$ и поэтому при $\omega\rightarrow 0 \Rightarrow D_2\rightarrow 0$

ValeriyS
06.04.2023 09:02
#25416440
+1
Если система представима в виде конечного и вычисляемого набора нулей и полюсов, то необходимым и достаточным критерием устойчивости является отсутствие полюсов в правой полуплоскости, или я что-то упустил в этом утверждении?

Я предполагаю, что:

- количество нулей равно количеству полюсов

- общий знак для gain выбран правильно для обеспечения отрицательной обратной связи

Sergeant101
06.04.2023 09:02
#25416876
О! Его величество ТАУ - сопромат от мира систем управления!

Годограф Михайлова.

Хотя мне лично больше ЛАЧХ нравится.

Зачем это здесь?

Автоматчика это совершенно отдельная профессия никак не связанная с программированием, даже промышленным.

Уж я то это вам гарантирую.

Вам с таким на форум математиков надо, желательно сдвинутых. )))
1. petuhoff Автор
  06.04.2023 09:02
  #25416936
  Не соглашусь вот тут система управления готовая к заливке в контроллеры в виде управляющего ПО:

6.4 Устойчивость систем автоматического регулирования. Частотный критерий устойчивости Михайлова +17

6.4. Частотный критерий устойчивости Михайлова

Предельный случай

Пример

Комментарии (5)

Nikeware

petuhoff Автор

ValeriyS

Sergeant101

petuhoff Автор