Без Фортуны, богини удачи, не обходились ни одно сражение, ни одна экспедиция или начинание, ни одна победа. Боги и люди молили ее быть на их стороне, строили посвященные ей храмы. И проклинали за изменчивость и непостоянство, но продолжали молить. За тысячелетия имена многих богов забылись, немногие остались на страницах фэнтезийных романов и марвеловских комиксов. Но и сегодня не найдется на планете человека, который не просил бы удачу улыбнуться ему. Боги умерли, их заменили наши знания. Богиню плодородия заменили удобрения, Посейдона — прогноз погоды, богиню любви — порноиндустрия. Даже Афина, богиня разума, растворилась в знаниях. Но удаче продолжают молиться все. Живучесть богини объясняется просто, она воплощает один из фундаментальных законов нашей реальности.

В отличии от знаменитого Е=мс2 или закона сохранения энергии, этот закон не так распиарен и странно называется: центральная предельная теорема. А для непосвященных ее определение и вовсе звучит загадочно: сумма многих слабо связанных величин, имеет распределение близкое к нормальному. Тем не менее, это утверждение определяет то, как из прошлого получается будущее в макромире, в мире где мы живем. Более того, оно определяет какими мы будем — высокими или низкими, толстыми или худыми, глупыми или умными.

Выглядит нормальное распределение вероятности событий как перевернутый колокол (уж не обессудьте за мои художественные способности):

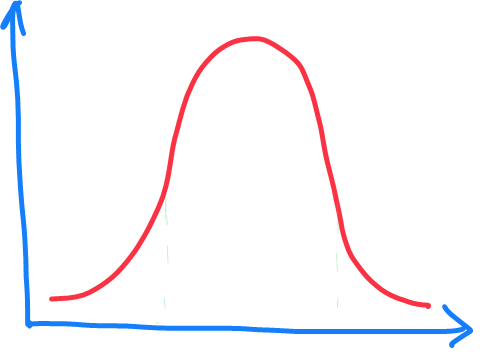
Что означает — есть события маловероятные, они по краям распределения. А есть обычные события; они как раз составляют основную часть распределения. Так вот, если вы надеялись не умереть во время пандемии от ковида, то вы просили фортуну поместить вас в середину распределения, а если мечтали об большом выигрыше, то просили удачу поместить в конец распределения. Но богиня не подчинялась даже могущественным богам, а людские просьбы ее тем более мало волнуют. Поэтому и мы отвлечемся от вечного человеческого нытья, и рассмотрим поподробнее то, как нормальное распределение формирует наши тела и наши способности.

Нормальное распределение практически универсальный закон природы и встречается буквально везде. Будете ли вы подсчитывать размеры песчинок или вероятности выпадения чисел на костях или изучать броуновское движение, всегда будет получаться нормальное распределение. Можно сказать, что нормальное распределение вшито в физику нашего мира. Аналогично обстоят дела и в биологии; что бы вы не считали рост человека или количество волос на хвосте льва всегда будет получаться нормальное распределение. Может показаться что распределение у живых определяется внешними случайными факторами, но стоит приглядеться повнимательнее, как оказывается, что все не так просто (вообще‑то полезно повнимательнее присматриваться, казалось бы, к простым вещам, часто за ними кроется много интересного). За нормальным распределением у живых стоят нетривиальные генетические механизмы. Наши гены, уже на заре эволюции поняли, насколько ненадежна и переменчива удача и сумели разработать механизмы, компенсирующие непредсказуемость будущего.

Давайте повнимательнее приглядимся к нам любимым, например посмотрев в зеркало. Что мы можем увидеть на лице? В глаза сразу бросается два глаза, расположенных по горизонтальной линии. Расстояние между глазами вариативно внутри человеческой популяции, у кого‑то они близко поставлены, у кого‑то широко расставлены. Статистически они будут распределены по нормальному распределению. Но у нас не бывает шести глаз или одного глаза, глаза не расположены друг над другом, не растут на ладонях или на пупке. Понятно почему это так, с глазами на пупке долго не проживешь и не успеешь оставить потомство. Но такие мутанты и не рождаются, что означает гены умеют держать свою вариативность под контролем. Гены жестко фиксируют одни параметры, а другим позволяют быть вариативными. Что означает, наша изменчивость не только результат воздействия случайных внешних факторов, а регулируется генетически.

Ещё более наглядный пример — половой диморфизм. (Дабы меня не обвинили в злостном антифеминизме, здесь и далее обсуждается половой диморфизм бабуинов. Любые совпадения с человеками случайны.) Если мы возьмем распределение некоего параметра, например уровня IQ отдельно для самок и отдельно для самцов, то окажется что мужское распределение с более широкими краями (признаюсь, я не знаю пытались ли измерять IQ у бабуинов).

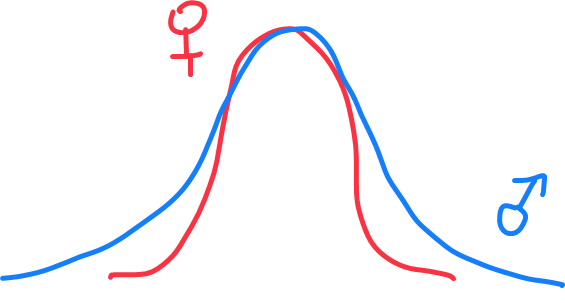
Что означает, бабуины с наибольшим и наименьшим параметром — это самцы. По любому параметру будут такие же результаты: самые умные и самые глупые — это самцы, самые бородатые и самые безбородые — это самцы, самые лопоухие и безухие — это самцы. И кстати, поэтому смертность среди новорожденных и нерожденных у самцов выше в несколько раз. А у самок разброс по параметрам наименьший, они очень консервативны. И это касается не только человеческой популяции, практически у всех живых организмов, у которых два пола, наблюдается подобный диморфизм (конечно есть исключения). Вернее, у тех организмов, у которых наблюдается половой диморфизм, будет наблюдаться аналогичная картина.

Главный приоритет у самок обеспечивать сохранение популяции, поэтому они должны быть максимально приспособленными к текущей ситуации. Произвести яйцеклетку стоит очень дорого, намного дороже чем сперматозоиды. Соответственно основная генетическая функция самцов обеспечивать разнообразие популяции. Они элементарно дешевле в производстве и воспроизведении. Даже если останется один единственный самец в популяции, он сможет обеспечить ее восстановление. Поэтому самцы более расходный материал. Если внешние факторы будут способствовать какой‑нибудь особенности самцов, например лопоухости, то благодаря такому распределению ролей за несколько поколений все станут лопоухими. Фактически самцы тянут всю популяцию в сторону максимальной приспособленности к изменениям во внешней среде. Вышесказанное означает, что дисперсия распределения сцеплена с полом организма, что опять же подтверждает утверждение, что нормальное распределение у живых обусловлено генами, а не результат случайных внешних воздействий.

Главный вопрос, каким образом реализуется этот механизм среди популяции? Кто решает кто какого будет роста? Как определяется кому достанется счастливый билет, а кому не очень? Нужно понимать, что нет никакой корреляции между организмами, гены каждого из нас независимо определяют параметры нашего тела и тем не менее, по итогу, все мы выстраиваемся вдоль гаусовской кривой. По‑видимому, где‑то в глубине нашего организма реализован механизм аналогичный генератору псевдослучайных чисел. Механизм этот сложный и мы только подступили к его изучению, пока нет ясности какие процессы в клетках могут отвечать за него. Но есть предположения.

Думаю, многие обращали внимание, что стоит углубиться в изучение какого‑нибудь процесса в генах, как все становится сложным и запутанным. На любой процесс постоянно действует множество факторов, влияющих и зависящих друг от друга. Например, процесс производства соматотропина (гормон роста). Гены, ответственные за его производство, расположены в 5 соседних участках 17 хромосомы. Так что одновременно могут печататься несколько копий. При этом две из них отличаются от остальных (видимо предназначены для специфических органов). Казалось бы, все просто. Но, не тут‑то было. Чтобы запустился процесс транскрипции соматотропина, множество разных факторов молекул, должны провзаимодействовать. Один запускает процесс, другой тормозит его, но запускает третий процесс, который вызывает каскад реакций, четвертая из которых блокирует второй фактор, а шестая ускоряет первый и тп и тд. Причем каждый из этих процессов влияет еще на что‑то. И все они дублируются и переплетаются самым загадочным образом. Причем многие факторы производятся в других клетках или расположены на других хромосомах. А еще не забываем, что соматотопин состоит из 191 аминокислоты и их всех нужно соединять и укладывать в 3D в правильном порядке. И смотришь на это все и думаешь какой гений составлял сей сложный код реализации?

Однако сложность эта намеренная и код этот действительно гениальный. Во‑первых, сложность выполняет функцию фильтра, который отсеивает случайные сигналы. А во‑вторых, она сама генерирует необходимую случайность. Именно она обеспечивает с одной стороны постоянство форм организмов, а с другой стороны их вариабельность.

Тут внимательный читатель скажет, про мутации и разные там гены с аллелями мы в школе проходили и их комбинаторика понятна. Но только вот гены — это участки ДНК, кодирующие белки. Все, что мы учили про мутации, касаются как раз структуры белков. Но только вот кучи белков недостаточно, чтобы построить организм. Помимо этого, еще нужно знать какие белки в какое время в каком месте и в каких количествах производить, а потом еще их выстраивать в правильном порядке. За данный процесс отвечает остальная часть ДНК, которую вначале назвали мусорной. Это так называя мусорная ДНК составляет 80–95% всего кода и определяет какими в итоге мы получимся (конечно же совместно с внешними условиями). Соответствующая наука называется эпигенетикой.

Вернемся к главному вопросу, как получить нормальное распределение? Возьмём шестигранный кубик и будем его бросать. Бросающий выступает в роли генератора случайных чисел. Вероятность выпадения любого числа одинаковая и равна 1/6. Но стоит нам взять два кубика картинка меняется теперь есть маловероятные события (2 или 12) и более вероятные (7). Чем больше у нас кубиков и чем больше на них граней, тем больше наше распределение будет приближаться к нормальному. Если у нас один человек бросает все кубики между ними может быть корреляция, связанная с бросающим. Чтобы этого избежать возьмем несколько человек и каждому дадим по одному кубику. Более того разведем их по разным углам вот так пусть бросают. Бросающие и является нашим генератором случайных чисел. То есть если у нас есть несколько несвязных факторов (кубики), результат которых неким образом учитывается вместе (не обязательно быть простому суммированию), то мы получили в итоге результат, близкий к нормальному распределению.

Думаю, аналогия понятная и, по‑видимому, в генах процессы реализованы подобным образом. Несколько факторов независящих друг от друга в итоге будут давать нужное распределение. И чем больше этих факторов и чем больше они разнесены друг от друга, тем более конечный результат будет ближе к нормальному распределению.

Другой вопрос, почему вариабельность раз она определяется генетически реализует именно нормальное распределение, а не какое‑нибудь другое? Возможно, когда появились первые клетки, распределение могло быть произвольным. Но так как именно нормальное распределение наиболее адекватно отражает реальность, оно жестко прописалась в генах. Есть частые внешние события, а есть редкие и случаются они согласно нормальному распределению. Невыгодно держать много особей, приспособленных под редкие события, они плохо приспособлены к текущей ситуации. Поэтому, всегда нужно большинство середнячков, а по краям пусть будут гении и дураки. Причем последние могут поменяться местами если внешние условия поменяются. И обеспечат приспособление всей популяции к новым условиям. Гены нашли правильный ответ на вопрос: как всегда выигрывать в казино? Нужно стать владельцем казино и самому генерировать случайности. И эта стратегия позволяет жизни существовать на нашей планете последние 4 миллиарда лет, невзирая ни на какие случайности и катастрофы.

Если вам повезло, и вы оказались на правильном конце распределения, это не благодаря вам, а благодаря удаче, которая вытащила вам выгодный билет. Гордиться своими способностями — это то же самое что гордится своим высоким ростом, в этом нет никакой заслуги индивидуума. Природа — бережливая старушка, она никогда ничего не выкидывает, и поэтому всегда будут рождаться низкие и высокие, худые и толстые, умные и глупые. Если вам повезло, и вы родились с подходящим для сегодняшней ситуации набором параметров, значит кто‑то другой оказался на другой стороне распределения. Это фундаментальный закон природы. Мы не можем его поменять, но мы можем протянуть руку помощи тем, кому в данный момент не везет. Ведь мы не знаем, что будет завтра, а фортуна очень своенравная девушка с черным юмором.