Семейство SHA

SHA (Алгоритмы безопасного хеширования) – это семейство криптографических хэш-функций, способных принимать сообщения произвольной длины и вычислять уникальный хэш-код фиксированной длины. Хэш-код SHA может быть использован для проверки целостности сообщения, а также для генерации цифровой подписи сообщения. На данный момент существует несколько стандартов безопасного алгоритма, каждый последующий включает более надёжные хэш-функции:

• SHA-0 – исходная версия 160-битной хеш-функции, опубликованной в 1993 году под названием «SHA»

• SHA-1 – исправленная версия SHA-0, опубликованная в 1995 году.

• SHA-2 – набор криптографических хэш-функций, впервые опубликованный в 2001 году. Включает в себя несколько размеров ключа, включая SHA-256, SHA-384 и SHA-512. Считается более безопасным, чем SHA-1, и рекомендуется для использования в новых системах.

• SHA-3 – последняя версия семейства хэш-функций SHA, ранее называвшаяся Keccak , выбранная в 2012 году после публичного конкурса среди разработчиков. Он поддерживает те же длины хэшей, что и SHA-2, но представляет собой новую хэш-функцию, которая отличается от SHA-1 и SHA-2.

SHA-256 относится к стандарту SHA-2, использует размер слова в 32 бита. Окончание 256 означает, что фиксированный размер хэша для любого сообщения равен 256 бит.

Структуры Меркла - Дамгарда

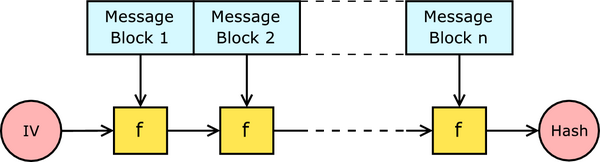
Хеш-функции семейства SHA-2 построены на основе структуры Меркла - Дамгарда. Это метод построения криптографических хэш-функций. Входное сообщение произвольной длины преобразуется в выходное сообщение фиксированной длины. Достигается это путём разбиения входного сообщение на блоки одинакового размера. После чего по очереди функция сжатия преобразовывает входное сообщение фиксированной длины в более короткое выходное сообщение фиксированной длины, каждый раз принимая входной блок с выходным от предыдущего раунда.

Ниже представлена односторонняя функция сжатия (f), она преобразует два входных блока фиксированной длины в выходной блок фиксированной длины. Алгоритм начинается с начального значения или вектора инициализации (IV). Для каждого блока сообщения, функция сжатия принимает результат предыдущего раунда и блок сообщения, и производит промежуточный результат.

Образование вектора инициализации

Вектор инициализации – фиксированное значение, в рассматриваемом алгоритме состоит из восьми констант по 32 бита.

• h0 = 0x6a09e667

• h1 = 0xbb67ae85

• h2 = 0x3c6ef372

• h3 = 0xa54ff53a

• h4 = 0x510e527f

• h5 = 0x9b05688c

• h6 = 0x1f83d9ab

• h7 = 0x5be0cd19

Константы были выбраны таким образом, чтобы добиться высокой степени диффузии и нелинейности в процессе хеширования. Конкретные значения были выбраны на основе обнаружения "безопасности Крипто", который состоит в том, чтобы выбирать значения, которые создаются случайными и которые не могут быть предсказаны или использованы для создания коллизий. В основе лежит функция, которая преобразует, первые 32 бита дробной части квадратного корня первых восьми простых чисел.

Пример получения h0:

Первое простое число – 2. Квадратный корень из 2 в двоичном 64 битном виде представлен на рисунке ниже. Необходимо найти дробную часть и выделить из неё первые 32 бита. Полученное число должно соответствовать – 0x6a09e667.

Данный вектор приставляет из себя начальное значение хэша, после проведения алгоритма их значения изменятся и сумма этих констант станет итоговым хэшем.

Создание блока

Блоки SHA-256 имеют фиксированный размер 512 бит, в порядке расположения байтов "big-endian". Если длина сообщения превышает размеры блока, создаются дополнительные блоки, до тех пор, пока сообщение полностью не разместиться. Если сообщение полностью не заполняет блок, необходимо дополнить последний блок до полного определёнными данными (обычно нулями).  Однако, есть вероятность, что различные сообщения, начинающиеся одними и теми же символами, и заканчивающимися нулями или другими байтами из заполнителя, будут поступать в функцию сжатия совершенно одинаковыми блоками. В результате чего получиться одинаковая хэш-сумма. Избежать этого помогает вставка иного значения первого бита заполнителя.  Так как заполнитель обычно состоит из нулей, первый бит заполнителя должен быть заменён на «1». В конце последнего блока зарезервировано 8 байт для длины исходного сообщения в битах. Алгоритм работает с каждым блоком по отдельности.

Пример сообщения: «ABCDEFGHIJKLMNOPQRASTUVWXYZabcdifghijklmnopqrstuvwxyz01»

«ABCDEFGHIJKLMNOPQRASTUVWXYZabcdifghijklmnopqrstuvwxyz012»

Как видно, на практике минимальный размер сообщения для использования только одного блока составляет 440 бит. Это связано с тем, что алгоритм всегда добавляет дополнительный бит «1», информацию о котором можно передать только в байте (символы, как и другие типы данных, могут занимать место кратное 8 битам). Соответственно поэтому при добавлении ещё одного символа, в блоке не остаётся места под 64 битную информацию о длине сообщения. Из-за чего создаётся второй блок запененный нулями.

Далее алгоритм будет работать индивидуально с каждым блоком по очереди.

На данном этапе все блоки имеют начальный вид, представленный в виде массива состоящего из 16 слов (от 0 до 15) по 32 бита. Полный размер блока в SHA-256 составляет 64 слова.

Ниже представлена функция на языке программирования С++, которая формирует и заполняет блоки:

//количество символов в строке
int64_t lenstr = message.size();
//раззмер поля длины в байтах
uint8_t field_len = 8;
//количество бит в строке
uint64_t bitstr = lenstr * 8;

//полезная нагрузка в байтах
uint64_t payload = message.size() + field_len;
//заполнитель в батах
uint64_t padding = 64 - payload % 64;
//количесво блоков
uint64_t block_count = payload / 64 + 1;

//инициализация блоков
std::vector<std::array <uint32_t, 64>> blocks(block_count);

//заполнение блоков
for (int64_t i = 0; i < block_count; i++)
{
    //массив каждого блока по 32 бита представляется как массив по 8 бит
    char* byte_block = (char*)&(blocks[i]);
    
    //обход элементов массива
    for (int j = 0 ; j < 64; j++)
    {
        if (lenstr == 0)
        {
            //заполнение блока отступами
            if (padding!=0)
            {
                *(byte_block + j) = 0x00;
                padding--;
            }
            //заполнение поля - "длины сообщения"
            else 
            {
                field_len--;
                *(byte_block + j) = bitstr >> (8 * field_len);
            }
        }
        else
        {
            //заполнение массива символоми сообщения
            *(byte_block + j) = message[j + i * 64];

            lenstr--;
            
            //если сообщение закончилось, вставляется первый байт заполнителя с "1" в начале
            if (lenstr == 0)
            {
                j++;
                *(byte_block + j) = 0x80;
                padding--;
            }
        }
    }
}

Для большинства машин, данный код заполонит блоки в порядке "little-endian", поэтому необходимо будет конвертировать каждое слово в порядок "big-endian":

void little_to_big_convert(uint32_t &word)
{
	word = (word >> 24) | ((word >> 8) & 0xff00)
		| ((word << 8) & 0xff0000) | (word << 24);
}

Расширение блока

Далее происходит заполнение новых слов в блоки. Так как их значение зависит от значений уже имеющихся слов, необходимо добиться правильного расположения байтов до этого этапа. Формирование каждого последующего слова происходит по формуле:

w[n] = w[n-16] +c0+w[n-7]+c1,

где w – массив слов, n – номер индекса слова, (+) – оператор сложения(не по модулю 2, происходит переполнение), c0,c1 – функции.

c0 = right_rotate(w[n-15], 7) ^ right_rotate(w[n-15], 18) ^ right_shift(w[n-15], 3),

c1 = right_rotate(w[n-2], 17) ^ right_rotate(w[n-2], 19) ^ right_shift(w[n-2], 10),

где right_rotate – функция реализующая правое вращение бит, принимающая 32-битное слово и центр вращения данного слова, right_shift – функция побитового сдвига в право, принимающая 32-битное слово и количество сдвигаемых бит, (^) – операция xor.

Реализация функций:

int RightRotate32(uint32_t n, uint32_t d)
{
	return (n >> d) | (n << (32 - d));
}

uint32_t C0(uint32_t word)
{
	return RightRotate32(word, 7) ^ RightRotate32(word, 18) ^ (word >> 3);
}

uint32_t C1(uint32_t word)
{
	return RightRotate32(word, 17) ^ RightRotate32(word, 19) ^ (word >> 10);
}

void ExpensionBlock(std::array<uint32_t, 64> &block)
{
	for (int i = 16; i < 64; i++)
	{
		block[i] = block[i - 16] + C0(block[i - 15]) + block[i - 7] + C1(block[i - 2]);
	}
}

Функция сжатия

Алгоритм пропускает каждый блок сообщения через цикл с 64 итерациями (раундами). В каждом раунде учувствуют слова из блока попарно с новым массивом констант по порядку.

Новые константы схожи по построению с начальным значением хэша, но на этот раз это первые 32 бита дробных частей кубических корней первых 64 простых чисел от 2 до 311.

Помимо них в каждом раунде принимают участие переменные, на старте инициализированные начальным значением хэша:

  a = h0, b = h1, c = h2, d = h3, e = h4, f = h5, g = h6, h = h7

В конце каждого раунда значение этих переменных будет отличаться от их значения в начале раунда, благодаря множественным преобразованиям. Преобразования, используемые на каждой итерации цикла для одного блока – это и есть функция сжатия Sha-256.

Преобразование переменных на каждой итерации одинаковые и осуществляется по правилу:

1. h = g

2. g = f

3. f = e

4. e = d + Temp1

5. d = c

6. c = b

7. b = a

8. a = Temp1 + Temp2

   1. Temp1 = h + Σ1 + Choice + k[i] + w[i]

   2. Temp2 = Σ0 + Majority

      1. k – массив констант

      2. w – массив слов из блока

      3. 1.3. i – итерация цикла,

      4. Σ0 = right_rotate(a, 2) ^ right_rotate(a, 13) ^ right_rotate(a, 22)

      5. Σ1= right_rotate(a, 6) ^ right_rotate(a, 11) ^ right_rotate(a, 25)

      6. Choice = (e & f) ^ ((!e) & g)

      7. Majority = (a & b) ^ (a & c) ^ (b & c),

         1. ! – инверсия бит

         2. & – побитовый оператор «и»

Значения, которые были получены на последней итерации цикла, складываются со старым и образуют новый вектор инициализации, который станет стартовым для следующего блока.

h0+=a, h1+=b, h2+=c, h3+=d, h4+=e, h5+=f, h6+=g, h7+=h

Если данный блок был последним, то сумма элементов этого вектора станет итоговым хэшем сообщения

  h0+ h1+ h2+ h3+ h4+ h5+ h6+ h7=hash_sha-256

Функция сжатия:

void compress(std::array<uint32_t, 64> w, std::array<uint32_t, 8> &H)
{
	const std::array<uint32_t, 64> K = {
		0x428a2f98,0x71374491,0xb5c0fbcf,0xe9b5dba5,
		0x3956c25b,0x59f111f1,0x923f82a4,0xab1c5ed5,
		0xd807aa98,0x12835b01,0x243185be,0x550c7dc3,
		0x72be5d74,0x80deb1fe,0x9bdc06a7,0xc19bf174,
		0xe49b69c1,0xefbe4786,0x0fc19dc6,0x240ca1cc,
		0x2de92c6f,0x4a7484aa,0x5cb0a9dc,0x76f988da,
		0x983e5152,0xa831c66d,0xb00327c8,0xbf597fc7,
		0xc6e00bf3,0xd5a79147,0x06ca6351,0x14292967,
		0x27b70a85,0x2e1b2138,0x4d2c6dfc,0x53380d13,
		0x650a7354,0x766a0abb,0x81c2c92e,0x92722c85,
		0xa2bfe8a1,0xa81a664b,0xc24b8b70,0xc76c51a3,
		0xd192e819,0xd6990624,0xf40e3585,0x106aa070,
		0x19a4c116,0x1e376c08,0x2748774c,0x34b0bcb5,
		0x391c0cb3,0x4ed8aa4a,0x5b9cca4f,0x682e6ff3,
		0x748f82ee,0x78a5636f,0x84c87814,0x8cc70208,
		0x90befffa,0xa4506ceb,0xbef9a3f7,0xc67178f2
	};

	uint32_t a = H[0];
	uint32_t b = H[1];
	uint32_t c = H[2];
	uint32_t d = H[3];
	uint32_t e = H[4];
	uint32_t f = H[5];
	uint32_t g = H[6];
	uint32_t h = H[7];

	for (size_t i = 0; i < 64; i++)
	{
		uint32_t Temp1 = h + Sum1(e) + Choice(e,f,g) + K[i] + w[i];
		uint32_t Temp2 = Sum0(a) + Majority(a, b, c);

		h = g;
		g = f;
		f = e;
		e = d + Temp1;
		d = c;
		c = b;
		b = a;
		a = Temp1 + Temp2;
	}
  
	H[0]+=a;
	H[1]+=b;
	H[2]+=c;
	H[3]+=d;
	H[4]+=e;
	H[5]+=f;
	H[6]+=g;
	H[7]+=h;
}

Вспомогательные функции:

uint32_t Sum0(uint32_t a)
{
	return RightRotate32(a, 2) ^ RightRotate32(a, 13) ^ RightRotate32(a, 22);
}
uint32_t Sum1(uint32_t e)
{
	return RightRotate32(e, 6) ^ RightRotate32(e, 11) ^ RightRotate32(e, 25);
}

uint32_t Choice(uint32_t e, uint32_t f, uint32_t g)
{
	return (e & f) ^ ((~e) & g);
}

uint32_t Majority(uint32_t a, uint32_t b, uint32_t c)
{
	return (a & b) ^ (a & c) ^ (b & c);
}

На примере сообщения: «ABCDEFGHIJKLMNOPQRASTUVWXYZabcdifghijklmnopqrstuvwxyz012»

Вектор инициализации, поступающий во второй блок, будет содержать следующие значения:

• ho=0x6b21d0db

• h1= 0x78b657db

• h2= 0x0e59599a

• h3= 0xd0d73fa5

• h4= 0x5f3a6d2d

• h5= 0xabf6e8d5

• h6= 0x1d443f62

• h7= 0x227abf9a

После обработки второго блока (последнего для данного сообщения), значения хэша будут равны:

• ho= 0x8da42cf0

• h1= 0x8db5e96a

• h2= 0x775d9620

• h3= 0x2fd22673

• h4= 0x16604e5e

• h5= 0xcc0cdb2d

• h6= 0x92ff4d60

• h7= 0xc65d3e36

Итоговым хэшэм сообщения будет: 0x8da42cf08db5e96a775d96202fd2267316604e5ecc0cdb2d92ff4d60c65d3e36

Пример построения главной функции хэширования:

std::array<uint32_t, 8> Hash(std::string message)
{
    //вектор инициализации
	std::array<uint32_t, 8> h = {
		0x6a09e667,0xbb67ae85,0x3c6ef372,0xa54ff53a,
		0x510e527f,0x9b05688c,0x1f83d9ab,0x5be0cd19
	};

	auto blocks = CreateBlock(message);

	for (auto& block : blocks)
	{
		compress(block, h);
	}

	return h;
}

Спасибо за прочтение!

Пожалуйста пишите в комментариях ваше мнение о статье. Нужна ли такая статья кому-нибудь сейчас? Какие есть недочёты по поводу оформления? Как можно улучшить код? Какие моменты были непоняты?