Здравствуйте,
Меня зовут Роман и я разрабатываю технологию извлечения смысла из математических формул.
Выглядит это как web редактор, в котором пользователь может писать формулы на языке, принятом среди математиков.
Во время работы наш редактор пытается понять смысл формулы и перевести ее на машиночитаемый язык. Если это невозможно, он показывает ошибки. Синтаксические и семантические. И еще он умеет уточнять смысл неоднозначных формул.
Сначала я хотел просто рассказать об этом продукте. Но это получалось скучно. Интересно только для тех, кто занимается сходной тематикой.
Поэтому я не буду рассказывать о самом продукте. Я расскажу несколько историй о том, как мы его делали. А точнее о том, как менялись наши представления о нём, как это отражалось на его модели данных и какими были побочные эффекты от неоптимального моделирования.
Думаю, что проблема правильного моделирования данных да и сами ошибки, которые мы совершали в процессе - тема более общая и она ближе, понятнее и может быть интересна не только узким специалистам.
Постановка задачи
В чем вообще проблема с извлечением смысла из формулы?
Есть много готовых редакторов, где можно написать формулу и получить на выходе выражение на Tex или MathML без семантики.
Проблема в том, что пользоваться такими выражениями очень сложно. Они ведь создавались не для записи смысла, а для нужд печатников.
Во-первых, если рассмотреть математику записанную Техом или MathML presentation в лоб, то это оказывается, контекстно-зависимый язык с экспоненциальным временем парсинга.
Во-вторых многие конструкции вообще нельзя интерпретировать однозначно:
y(x+1) - вызов функции или умножение?
(a,b) - точка или интервал?
Наконец, там разрешается писать любые последовательности символов.
Даже те, в которых вообще нет смысла.
+++, например
Разбор формул с ошибками еще сложнее, чем понимание смысла правильных формул.
Сложнее - в плане требований ко времени работы алгоритма, а не сложности его реализации. Мы ведь хотим не просто сломаться на неправильной формуле, мы хотим найти конкретное место, где сделана ошибка и рассказать пользователю в чем именно она заключается.
В рамках большого проекта системы для обучения студентов математическому анализу нам понадобилась технология ввода и редактирования формул с представлением результата в форме, которую легко интерпретировать.
Говоря более строго, нам нужен был редактор формул, который выдавал бы введенную человеком формулу на контекстно свободном языке. И делал это в реальном времени.
Поскольку на рынке таких редакторов не было, мы решили сделать свой, хотя и были на тот момент очень далеки от этой темы.
Теперь пару слов о модели данных.
Нам было понятно, что моделью будет какое-то дерево.
Которое будет состоять из разных математических “узлов”.
Часть этих узлов - терминалы, листочки дерева.
Например, переменные или числа.
А другая часть - нетерминалы - промежуточные узлы. Нетерминалы имеют “детей”. Например у синуса есть аргумент, а у предела целых три “потомка” - переменная, то к чему она стремится и формула.
И вот, на входе у нас есть дерево и грамматика контекстно свободного языка описания математических формул на котором мы хотели получить результат.
История первая - типизированные плэйсхолдеры
Эта история происходила в самом начале, когда мы делали первые шаги в понимании нашей предметной области.
И думали мы тогда примерно так:
У нас есть грамматика и желание ей соответствовать.
Редактор должен позволять ввод только семантически правильных формул.
Вот есть модель, соответствующая какой-то формуле.
Вот есть команда от пользователя (например, нажатие кнопки на клавиатуре).
Редактор должен понять эту команду и , если она имеет смысл, перестроить модель так, чтобы она снова соответствовала нашей грамматике.
У этого подхода есть очевидная нестыковка - формула не обязана иметь смысл после ввода каждой команды -
2+ , например, смысла не имеет.
Поэтому мы вводим в модель специальный элемент - плэйсхолдер.
В примере с 2+ после ввода плюса, наш редактор автоматически вставит плэйсхолдер и теперь он хочет считать выражение 2+_ хотя и недописанным, но соответствующим грамматике.
Чтобы выражение соответствовало грамматике, пусть плэйсхолдер будет типизированным - пусть он разрешает вместо себя вводить только то, что разрешено грамматикой в этом месте.
Например, для 2+_ в плэйсхолдер нельзя вводить множества, но можно вводить выражения.
А если пользователь напишет, например
x2
Редактор вставит между ними типизированный плэйсхолдер, разрешающий бинарные операции или функции:
x_2 -> x+2 или x sin 2
По мере ввода новых символов можно уточнять тип плэйсхолдера.
Например, если ввести сюда s:
x s 2
То это точно уже не бинарная операция, но пока и не функция.
Поэтому теперь тут будет плэйсхолдер, допускающий ввод функций и хранящий вот эту вот буковку s как незаконченный ввод.
Но тут возникают проблемы:
Как определить тип выражения пока ввод не закончен?
В процессе ввода тип может меняться!
Например, если посимвольно вводить
(1+2+3+4+5+6)*3
в плэйсхолдер, разрешающий ввод произведения, то понять, что вводится именно произведение можно только к концу ввода.
Что делать до этого момента? Неограниченно накапливать сырой ввод?
Как определить что ввод закончен?
Что делать с этой сырой строкой потом?
Выглядит как серьезная проблема.
Но этого мало.
Если мы по мере ввода сужаем разрешенный набор типов в плэйсхолдере, то что мы будем делать, когда пользователь начнет удалять ранее введенные символы?
Расширять допустимый набор типов обратно?
А если он удаляет символы в другом порядке?
Вот на этом месте нам разонравилась идея с типизированными плэйсхолдерами.
И мы решили поискать что-то другое.
Например, такое:
Модели можно не соответствовать грамматике в процессе работы. Проверять мы будем только арность (у синуса один потомок, у предела три)
Соответствие грамматике будем проверять по отдельному запросу пользователя
В случае несоответствия будем выдавать ошибку
Плэйсхолдеры не нужны
Ок.
Но если плэйсхолдеров нет, то как вообще моделировать недописанные выражения вроде:
x2
x- переменная. Терминал. Листик дерева.
2 - тоже терминал и тоже листик.
Смысла в таком выражении нет.
Но пользователь взял и так написал. А значит нам нужно построить какое-то дерево.
И вот здесь мы придумали универсальный соединитель - специальный невидимый нетерминал с двумя потомками, предназначенный для соединения стоящих рядом конструкций.

Интересно, что если написать это выражение в другом порядке:
2x
то оно имеет математический смысл - это неявно написанное умножение.
Выходит, в некоторых случаях универсальный соединитель имеет смысл и может соответствовать грамматике. А в некоторых нет. И когда ввод выражения завершен соединители должны остаться только там, где они понимаются как умножения. Соединитель в другом месте - ошибка.
Есть еще один вопрос. Что, делать с символами, которые можно вводить, потому что они являются частью каких-то математических структур, но сами по себе они не имеют никакого смысла. Как моделировать их в дереве?
Специально для таких символов в модели появился новый односимвольный терминал - Raw.
Хотя идея с типизированными плэйсхолдерами была совершенно негодной, поиграв с ней, мы начали процесс понимания нашей предметной области - стало ясно, что попытка обеспечить постоянное соответствие модели грамматике не работает.
Кроме этого мы ввели в модель две важные конструкции, которые есть там до сих пор - нетерминал - универсальный соединитель и терминал - сырой непонятый пока символ.
История вторая - невалидность внешняя и внутренняя
Мне всегда не нравились штуки, которые пытаются думать за пользователя.
Может мне не везло, но они обычно думали неправильно.
Нет ничего хуже текстового редактора упорно заменяющего введенную тобой букву на заглавную.
Наш редактор так вести себя не должен - если есть ошибка в формуле, надо ее показать, но вот вставлять за пользователя скобки там, где он не просил или еще как-то предугадывать его намерения - не наше дело.
Однако мы все-таки столкнулись с одной интересной ситуацией.
Модель была явно ошибочной, но пользователь не мог сам исправить эту ошибку.
Потому, что ошибочная модель визуально выглядела также, как и правильная.
Если пользователь видит sin, он думает, что это синус. И если система думает, что это произведение трех переменных s, i и n , то перед нами один из примеров такой ситуации.
Эту историю надо было обрабатывать как-то автоматически.
То есть надо было приводить модель к такому виду, чтобы понимание формулы нашей программкой и нашим пользователем было одинаковым.
Мы назвали такую ситуацию “внутренней невалидностью” - в отличие от “внешней невалидности” (типа 2+++) , явно видимой пользователю.
Оказалось, что внутренних невалидностей, по крайней мере, несколько. И все они связаны с невидимыми штуками вроде универсального соединителя.
Как я уже сказал, пользователь такие ситуации исправить не может.
Поэтому мы должны делать это за него.
Механизм примерно такой -
Пользователь нажимает какую-то кнопочку.
Мы делаем “наивную” вставку в дерево. Ну или наивное удаление.
Затем запускаем некую штуку, которая должна исправить внутренние невалидности.
А штука получилась в общих чертах такая:
Есть два основных алгоритма - поворот, следящий за приоритетами операций и выбрасыватель лишних соединителей, который просто заменяет поддеревья вида
join(x,null) на x
Лучше пояснить на примере.
Пусть у нас написано:
2x
Мы ставим курсор между ними и вставляем сюда плюс.
Изначальное дерево такое:

После наивной вставки плюса через универсальный соединитель получаем явно неверную модель, но выражение для пользователя выглядит корректно:

Выбросить из этого дерева join нельзя. Поэтому применяем второй алгоритм - поворот.
Поворот меняет структуру дерева так, чтобы можно было выполнять все операции последовательно от листиков дерева к его вершине и при этом соблюдались бы приоритеты операций. Заметим, что приоритет join - выше (так как join еще и умножение). Но плюс стоит в дереве ниже соединителя и значит рискует быть выполненным раньше.
Поэтому поворот такого дерева даст вот это:

И теперь сработает выбрасыватель join:

И снова поворот:

И снова выбрасыватель:

Получается, что такой вот примитивный алгоритм исправляет нашу модель. Теперь она соответствует тому, что думает о ней пользователь.
Конечно, видов внутренней невалидности больше. И алгоритмов ее исправляющих тоже.
Кроме того, простой поворот не справляется с некоторыми видами деревьев и поэтому наш поворот больше похож на повороты, применяемые для балансировки АВЛ деревьев.
Но в целом, описанный выше алгоритм - в каком-то смысле ядро всей системы.
История третья - эволюция нетерминалов
До этого мы говорили о модели математического выражения.
А сейчас я хочу поговорить о моделировании курсора.
Нам необходимо как-то указать редактору куда мы хотим что-то вставить или откуда удалить.
Модель - это дерево. И состоит оно из терминалов и нетерминалов.
Указатель на терминал - это относительно просто. Нужно знать только сам терминал и индекс внутри него.
С нетерминалами чуть сложнее.
Изначально мы думали так:
Вот есть, например, предел. Там есть три потомка и два собственных литерала - lim и стрелочка. Если у предела уже есть потомки, то указатели на сам предел нам не нужны - мы будем ставить их на потомков.
Но вот пока предел “пустой”, нам надо как-то пометить вот эти все пустые места.
И мы решили, что указателем на нетерминал будет пара - литерал (lim или стрелочка) и признак слева-справа.
Таким образом мы сможем сказать редактору - вставь что-то справа от стрелочки. Или, например, обработай нажатие клавиши delete если курсор стоит слева от литерала lim.
На первый взгляд - нормальная схема.
Но на самом деле это было одно из худших решений.
Первая сложность выглядела так:
Есть возведение в степень. Это нетерминал. У него два потомка - то что возводится в степень и показатель степени.
Но пока там ничего нет сам нетерминал оказывается невидимым.
Ну, значит у него два невидимых литерала - сверху и снизу, решили мы.
И проблемы с указателями вроде как нет.
Справа от верхнего литерала - отличный же адрес.
До тех пор, пока туда не вставили что-то настоящее. Вроде циферки.
А вот когда вставили, наш верхний литерал теперь где? А его нет.
И адрес (справа от верхнего литерала) теперь не актуален.
Здесь мы получили прямо кучу проблем с поддержкой адресов. Наши указатели внезапно портились и требовали замены.
Потратив какое-то время на попытку как-то управлять этим хозяйством мы наконец решили обратить внимание на корень проблемы.
И увидели вот эту странную сущность - невидимые фантомные литералы.
Сущность была как-то совсем не очень.
Но, казалось бы, очевидная идея - ввести невидимый терминал-плэйсхолдер нами не рассматривалась. Мы ведь уже определили в первой истории, что плэйсхолдеры - это зло.
Задним числом это выглядит очевидным. Но в реале ответ становится очевидным только после того, как правильно поставлен вопрос.
В итоге фантомные невидимые литералы были убиты и заменены на односимвольные терминалы-плэйсхолдеры.
А чем они лучше? Ведь при замене плэйсхолдера на число возникает примерно та же проблема - устаревание указателя. На самом деле они намного лучше.
В случае терминалов плэйсхолдеров работает простое правило - указатель устарел тогда и только тогда, когда в модели больше нет узла, на который он указывает.
А в случае невидимых литералов простого правила нет. Сам нетерминал на месте. Логика обработки внезапно вырастает в разы.
С этой проблемой разобрались достаточно быстро.
Но была и еще одна.
Вот есть логика вставки в редактор и удаления из редактора.
Она примерно одна и та же в случае вставки в терминал и в нетерминал.
Но нам пришлось писать ее дважды, потому что наши указатели на терминал и на нетерминал были совершенно разными.
(Терминал, индекс)
(Нетерминал, литерал, справа-слева)
Это - еще один пример, когда плохая модель вызывает необходимость решения искусственно созданных задач.
Ущербность и искусственность понятия литералов была осознана не сразу.
Но в итоге их просто выбросили.
Вместо них появились приватные терминалы.
В чем разница? Литерал был частью нетерминала и требовал специальной адресации.
Приватный терминал - просто подвид терминала, который имеет право стоять только в своем нетерминале родителе. Указатель на приватный терминал не отличается от указателя на обычный терминал.
(Терминал, индекс)
Код для вставки внезапно сократился вдвое.
С удалением, правда, вышло чуть хуже. Удаление обычного терминала (числа или переменной) все же отличается от удаления приватного терминала (стрелочка в пределе, например).
Обычный терминал можно просто взять и удалить из дерева.
А вот приватный… Удалим стрелочку из предела. Что останется?
Удалять весь предел? А что с его потомками?
Здесь требуется другой подход.
Попытку удаления приватного терминала у нас обрабатывает его нетерминал-родитель. И он сам решает, что делать в каждом конкретном случае.
Может запретить удаление совсем.
Может удалить нетерминал со всеми потомками.
Может заменить нетерминал на одного из потомков (так, например действует нетерминал синус при удалении из него приватного терминала sin).
Наконец, можно спросить пользователя что именно он собирался удалить.
Все эти варианты у нас реализованы.
И вот. Несмотря на разную обработку удаления приватных и обычных терминалов отказ от литералов принес массу пользы.
Во-первых курсор теперь всегда записывался одинаково.
Во-вторых стало работать простое правило - если в дереве есть терминал, на который указывает курсор, значит курсор валиден.
В-третьих, наши нетерминалы стали классическими нетерминалами. Они стали полностью невидимыми. Теперь нетерминалы задают отношения между потомками. Все, как в классике.
История четвертая - актуализация семантического дерева и производная Лагранжа
Я уже говорил, что после наивной вставки или удаления элемента, мы запускаем специальные алгоритмы, меняющие наше дерево так, чтобы можно было понять его смысл - семантику выражения.
Во второй истории был описан самый основной из этих алгоритмов - основанный на приоритетах операций и поворотах.
Проблема возникла, когда число таких алгоритмов стало расти.
Ну вот, например, хочет человек написать производную dy/dx.
Он вводит d потом y. Это пока выглядит как произведение двух переменных.
Потом он вводит знак деления - теперь это недописанное (ошибочное) выражение.
Потом вводит d в знаменателе - теперь это дробь.
И наконец он вводит x и наши алгоритмы понимают, что видят производную.
В дереве меняются соответствующие узлы.
А потом пользователь, например, вставляет плюс между d и x.
И теперь сложные алгоритмы должны понять что это - больше не производная и перестроить все дерево обратно, снова заменив ее на дробь
Количество и сложность алгоритмов , перестраивающих дерево, начало расти.
К тому же мы увидели, что 90% их работы бессмысленно. Во время редактирования они создавали промежуточные структуры (как, например, дробь при вводе производной) и постоянно перегоняли дерево туда и обратно, замедляя работу.
Хуже того, каждый такой алгоритм срабатывал независимо, когда видел в дереве структуру, которую ему хотелось перестроить. Поэтому невозможно было гарантировать что алгоритмы не уйдут в бесконечный цикл, постоянно воюя за “свою” интерпретацию дерева.
Проблема опять была в неоптимальном моделировании.
Хотя наш редактор и модифицирует модель в ответ на вводимые пользователем изменения, вместо того, чтобы строить ее с нуля, как это делают классические компиляторы, у него с компиляторами много общего. И нашей ошибкой было попытка работать сразу с семантическим деревом, вместо дерева синтаксического разбора.
Дерево разбора не содержит семантики. Оно содержит синтаксическую структуру. Например, для выражения dy/dx разница между деревом разбора и семантическим деревом показана на рисунке.
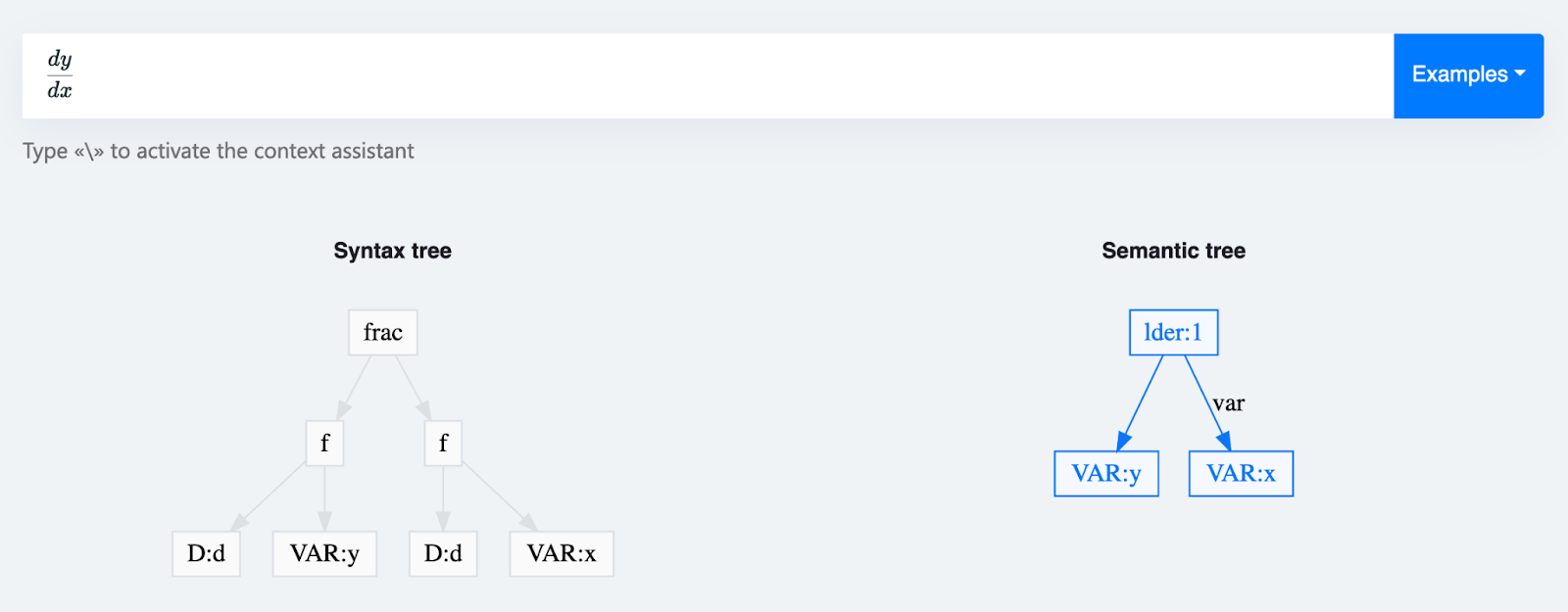
Поддерживать целостность дерева разбора многократно проще, чем семантического дерева. Для этого нужно всего несколько алгоритмов, которые не сложны, практически никогда не создают промежуточных структур, никогда не “воюют” друг с другом и очень просты для отладки.
С другой стороны, семантическое дерево всегда можно быстро построить из синтаксического.
Ну, почти всегда.
Потому что, во-первых, есть выражения, внешний вид которых не определяет их смысл однозначно. Например, вот такое:
y(x+1) Это произведение или вызов функции y?
А, во-вторых, никто не мешает пользователю вводить семантически неверные выражения, вроде:
2+++
Для правильной обработки неоднозначных выражений мы ввели контекст, в котором храним информацию, помогающую разрешать такие неоднозначности. Контекст используется при переводе синтаксического дерева в семантическое. Если нужной информации в нем пока нет, мы просто спрашиваем ее у пользователя - “вы имели в виду произведение или функцию?”
Для неверных выражений, при попытке получения семантики, мы находим ошибочные части и показываем их пользователю, поясняя что с ними не так.

Дополнительным плюсом перехода к модели из двух деревьев стали односимвольные терминалы в синтаксическом дереве.
Теперь, чтобы описать позицию курсора, вместо (указатель на терминал + индекс) мы работаем с (указатель на терминал + признак справа/слева от терминала).
Вот тут можно повводить различные выражения и посмотреть как перестраиваются синтаксическое и семантическое деревья.
История пятая - про выделения
В любом редакторе нужна возможность выделить часть выражения, чтобы скопировать его и вставить в другое место.
Хорошо, когда выделенная часть является поддеревом - выделил, вырезал поддерево, вставил в нужное место.
А если нет?
Вот простейший случай - дерево для выражения 1+2+3:

Выделяем 1+2 - все просто.
Выделяем 2+3 - а вот тут поддерева уже нет. Что тогда вырезать?
Можно поступить , например, так - обходим все элементы дерева в том же порядке, в каком они визуально отображаются редактором ( 1, +, 2 , +, 3) и , если элемент выделен, то копируем его в другой редактор, а если нет, то пропускаем.
Для этого примера все сработает. А как насчет такого?

Скопировав такую часть выражения, пользователь ожидает, что при вставке получится что-то такое:

Но наш наивный подход даст ему просто 2+3, что довольно неожиданно.
А еще не понятно, как поступить, если выделена только часть неделимой структуры - например, стрелочка от предела или только одна из парных скобок? Что надо вставить в новый редактор, если отдельно стрелочка не только не существует но и не имеет смысла?
Мы использовали здесь подход, близкий к обработке удаления приватных терминалов - когда пользователь выделяет какой-то терминал, то мы разрешаем родительскому нетерминалу расширить это выделение. Так, если пользователь выделил стрелочку от предела, нетерминал “предел” решает выделить также и символ lim,
А при выделении 2+3 в

нетерминал “степень” добавляет к выделению самого себя.
Расширение выделения происходит рекурсивно - по всем родителям. Таким образом, мы заставили нашу модель отвечать за “осмысленность” и “копируемость” сделанного пользователем выделения.
А дальше используем тот же наивный подход - обходим все элементы дерева в том порядке, в каком они визуально отображаются редактором и копируем выделенные терминалы по одному в пустой редактор. В пустом редакторе они собираются в дерево, которое потом можно “прицепить” в нужное место “целевого” редактора - того, в который мы хотим скопировать наше выделение.
Если в каких-то случаях вставленное выражение отличается от ожидаемого, просто меняем логику выделения соответствующего нетерминала.
История 6 - отображение формулы и топологическая модель
До сих пор я говорил про синтаксическую и семантическую модели. Но нам надо еще уметь рисовать нашу формулу, а дерево просто так не нарисуешь.
Поскольку нам хотелось уметь отрисовывать дерево различными рендерами (для web, для печати и т п) и при этом не повторять логику отрисовки в каждом из них, у нас появилась еще одна промежуточная модель - топологическая.
Она строилась по синтаксической модели и представляла собой абстрактную пространственную структуру, где было понятно взаимное расположение всех символов.
Очевидно, что такая топологическая структура не может быть линейной - множество выражений имеет несколько “этажей”. Например, степень имеет “второй этаж”, а предел - “минус первый”.
Поэтому наша топология состояла из горизонтальных строк, где одна из них находилась на “базовом” уровне, а остальные можно было прикреплять выше или ниже любого символа на любом уровне. Получалась такая древовидная структура, где ”ветки” росли вправо и расходились вверх и вниз от горизонтального “ствола”.
Что же с ней было не так?
Навигация при помощи курсорных клавиш.
Вопрос: куда надо переместить курсор если он стоит справа от символа “c”, а пользователь нажал стрелку вправо?
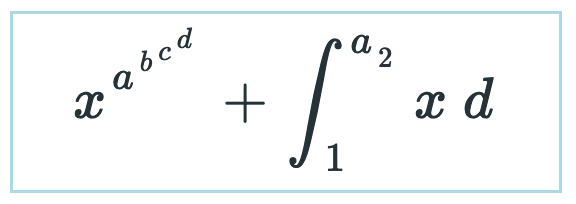
Поставить его перед буквой a из верхнего предела интеграла? А может перед двойкой - ее индексом?
Оказалось, что наша структурная модель вообще не может ответить на этот вопрос.
Потому, что физическая высота “этажей” во-первых разная, а во-вторых зависит от конкретного рендерера. А значит мы не можем использовать число этажей, чтобы найти символы из разных “веток”, стоящие на одной высоте.
Чтобы реализовать сколько-нибудь приличное поведение при навигации стрелочками, нам пришлось запрашивать у рендерера физические координаты каждого символа, что довольно серьезно усложняло логику.
Проблема решилась довольно неожиданно. В какой-то момент нам понадобилось поддержать ввод матриц.
И подход с нашей древовидной структурной моделью стал очевидно неадекватен новой задаче.
Зато после того, как мы переделали топологическую модель из древовидной-одномерной в древовидную-двумерную , решилась и проблема запутанной навигации по физическим координатам. Кода стало значительно меньше, а новая логика навигации стала нравиться нашим пользователям даже больше.
Выводы
Правильное моделирование - залог успеха. Или провала. Впрочем, это и так все знают.
Пока ты не понял глубоко свою предметную область, твоя модель скорее всего будет неправильная. С первой попытки. И со второй тоже.
Когда ты наконец нашел правильную модель, то точно знаешь что она правильна, потому что она внезапно приводит к кратному упрощению кода. И часто в самых неожиданных местах.
Правильная модель часто оказывается чем-то до боли знакомым - просто ты не сразу понял, что именно ты создаешь.
Мы вот думали, что пишем редактор математических формул, а по факту создавали компилятор с контекстно зависимого языка, который, в силу требований к скорости работы, вынужден был кэшировать и переиспользовать свои предыдущие результаты по мере редактирования выражения.
Если бы мы поняли это сразу, сэкономили бы много времени.
Поиграть с редактором можно тут:
P.S.
Если у вас есть проекты, где пригодится такая технология, вы видите что еще можно было бы упростить в нашей модели, или у вас есть какие-то мысли, идеи, предложения, напишите мне!
Комментарии (4)

sashagil
13.06.2023 11:51В плане accessibility - есть довольно интересная разрабока по диктовке математических формул - на случай, если вам будет любопытно: https://devblogs.microsoft.com/math-in-office/math-dictation/


belch84
Существует такой онлайн-построитель математических формул
http://mathurl.com/ live equation editing · permanent short links · LaTeX+AMS input
Смысл из формул они там извлекать не пытаются, просто можно воспользоваться очень небольшим набором стандартных конструкций, которые позволят любое выражение записать так, как нужно (наверное, это какой-то вариант синтаксиса TeX)
softaria Автор
Так-то редакторов много - https://en.wikipedia.org/wiki/Formula_editor
Фишка нашего как раз в понимании смысла. Можно использовать его, как frontend к CAS, а еще у него уровень accessibility оказался высоким - он может произнести формулу таким же образом, как это сделал бы человек. Не посимвольно. Это удобно для слабовидящих.