Если вы пишете свой язык программирования, то вы наверное слышали о type inference. В этом цикле статей, без лишней теории, мы наглядно разберем как это работает и реализуем свой на Rust.
Что такое type inference?
Type inference в контексте компиляторов - это стадия компиляции, в которой компилятор определяет типы для выражений. Type inference в основном присущ функциональным языкам, но и другие группы языков тоже могут его реализовывать.

Разбираем алгоритм
Дисклеймер: Здесь будет минимум теории и некоторые термины и определения могут быть не использованы.
Перед тем как производить анализ типов, нашему компилятору нужно спарсить наш исходник. И именно в этой статье мы будем по минимому использовать понятия AST и HIR и будем рассматривать type inference на примерах кода, а не деревьев.

Представим, что у нас есть код на гипотетическом языке программирования, для которого мы хотим реализовать вывод типов:
func inc(a) {
return a + 1;
}Так как в сигнатуре функции типы не указаны, нам придется определять их самим. Первое, что нам нужно сделать это создать переменные типов:
func inc(a: ?1) -> ?2 {
return a + 1;
}Переменная типа — в данном случае обозначает тип, которой мы еще не определили.
Для простоты и наглядности допустим что, сигнатура оператора + это: (int, int) -> int. Тогда, из a + 1 следует, что тип параметра a должен быть int и тип выражения 1 тоже должен быть int. А так как a + 1 равно int и является возвращаемым значением функции inc, то возвращаемое значение функции это int. Таким образом, мы получили информацию об взаимоотношениях между типами или type constraint-ы.
?1 = int
int = int
?2 = intType constraint - проще говоря, это способ записывать информацию о взаимоотношениях между типами.
Здесь мы используем равенство, но могли и использовать знаки неравенства, например для численных типов (что мы в этой статье делать не будем).
Теперь когда мы имеем список этих самых взаимоотношений, мы можем узнать значения переменных типов, это называется - unification (унификация). Суть в том, чтобы из системы уравнений, которая является списком type constraint-ов получить сами значения переменных типов:

У читателей мог возникнуть вопрос, что произойдет если у уравнения нет решения? Ответ прост - ошибка mismatched types. Например:

Так как String не может быть равен int, type constraint не соблюден и уравнение не имеет решений. Тогда мы можем увидеть ошибку mismatched types:
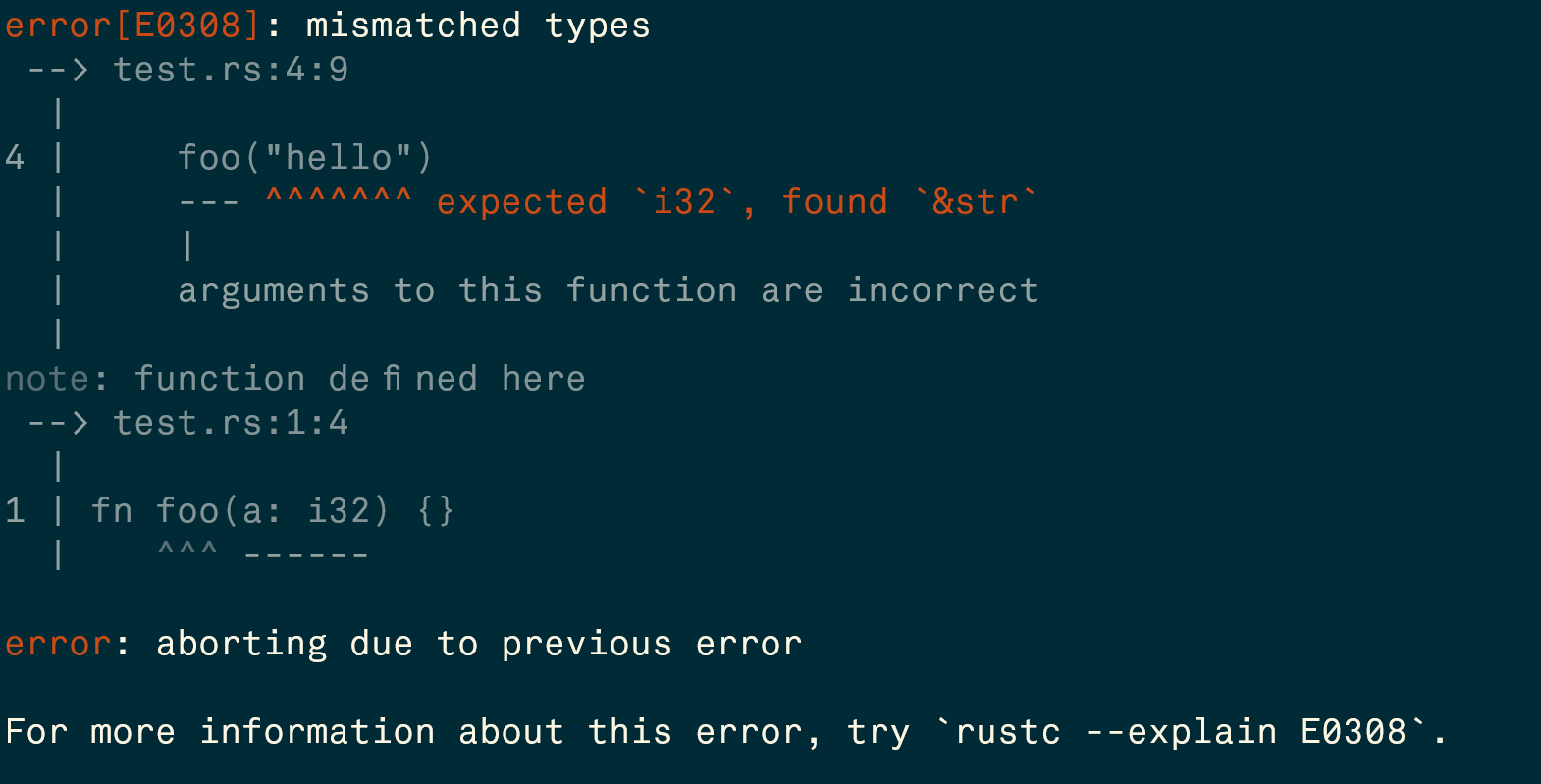
Возьмем пример поинтереснее:
func generate_nums(count) {
var a = [];
for (var i = 0; i < count; i++) {
a.insert(i);
}
return a;
}Сначала, как в прошлом примере разметим переменные типов для имен и сигнатуры функции:
func generate_nums(count: ?1) -> ?2 {
var a: ?3 = [];
for (var i: ?4 = 0; i < count; i++) {
a.insert(i);
}
return a;
}Теперь посмотрим на место где мы объявляем a - мы создаем пустой массив. Мы можем использовать переменную типа, для того чтобы обозначать тип элементов массива:
?3 = Array<?5>Идем дальше:
for (var i: ?4 = 0; i < count; i++) {Предположим, что сигнатура у оператора ++: (int) -> int и сигнатура у оператора <: (int, int) -> bool. Так, что у нас есть 3 новых constraint-а:
?4 = int
?4 = ?1
?4 = intПродолжим:
a.insert(i);Допустим метод insert у массива определен как-то так: List<T>.insert(element: T). Тогда для дженерика T нам нужна еще одна переменная типа:
?3 = Array<?6> // a
?6 = ?4 // iИ самое последнее:
func generate_nums(count: ?1) -> ?2 {
var a: ?3 = [];
...
return a;
}Возвращаемое значение функции это a, значит:
?3 = ?2Таким образом получаем систему уравнений:
?3 = Array<?5>
?4 = int
?4 = ?1
?4 = int
?3 = Array<?6>
?6 = ?4
?3 = ?2И снова, с помощью алгоритма унификации, мы можем решить данную систему уравнений и получить:
?1 = int
?2 = Array<int>
?3 = Array<int>
?4 = int
?5 = int
?6 = intПодставив эти типы получим результат type inference:
func generate_nums(count: int) -> Array<int> {
var a: Array<int> = [];
for (var i: int = 0; i < count; i++) {
a.insert(i);
}
return a;
}Теперь возможно у читателя появился вопрос, как работает этот загадочный алгоритм унификации который решает систему уравнений из type constraint-ов? Сейчас мы это разберем!
Unification algorithm (Алгоритм унификации)
Сначала напишем представление типов в нашем языке:
#[derive(Debug, Clone, PartialEq, Eq, PartialOrd, Ord, Hash)]
enum Type {
Constructor(TypeConstructor),
Variable(TypeVariable),
}
#[derive(Debug, Clone, PartialEq, Eq, PartialOrd, Ord, Hash)]
struct TypeConstructor {
name: String,
generics: Vec<Arc<Type>>,
}
#[derive(Debug, Clone, Copy, PartialEq, Eq, PartialOrd, Ord, Hash)]
struct TypeVariable(usize);То есть:
intэтоTypeConstructor { name: "int", generics: Vec::new() }.List<int>этоTypeConstructor { name: "List", generics: vec![ TypeConstructor { name: "int", generics: vec![] } ] }.?1этоTypeVariable(1).
Теперь мы можем преступать к реализации алгоритма унификации:
fn unify(left: Arc<Type>, right: Arc<Type>,
substitutions: &mut HashMap<TypeVariable, Arc<Type>>) {
match (left.as_ref(), right.as_ref()) {Если оба типа это type constructor-ы, то тогда проверяем то, что они равны и унифицируем их generic-и:
(
Type::Constructor(TypeConstructor {
name: name1,
generics: generics1,
}),
Type::Constructor(TypeConstructor {
name: name2,
generics: generics2,
}),
) => {
assert_eq!(name1, name2);
assert_eq!(generics1.len(), generics2.len());
for (left, right) in zip(generics1, generics2) {
unify(left.clone(), right.clone(), substitutions);
}
}Например из:
Array<int> = Array<?1>Следует, что:
int = ?1Если же мы получаем два разных type constructor-а, то тогда у нас type mismatch:
Array<?2> != Option<?3>Если обе стороны это равные переменные типов, то тогда все хорошо и мы ничего не делаем:
(Type::Variable(TypeVariable(i)),
Type::Variable(TypeVariable(j))) if i == j => {}Если же нет, то тогда мы добавляем значение переменной в хранилище и, что важно проверяем не создали ли мы бесконечный тип.
(_, Type::Variable(v @ TypeVariable(..))) => {
if let Some(substitution) = substitutions.get(&v) {
unify(left, substitution.clone(), substitutions);
return;
}
assert!(!v.occurs_in(left.clone(), substitutions));
substitutions.insert(*v, left);
}
(Type::Variable(v @ TypeVariable(..)), _) => {
if let Some(substitution) = substitutions.get(&v) {
unify(right, substitution.clone(), substitutions);
return;
}
assert!(!v.occurs_in(right.clone(), substitutions));
substitutions.insert(*v, right);
}Пример, случая когда мы пытаемся использовать бесконечный тип в Rust-е:
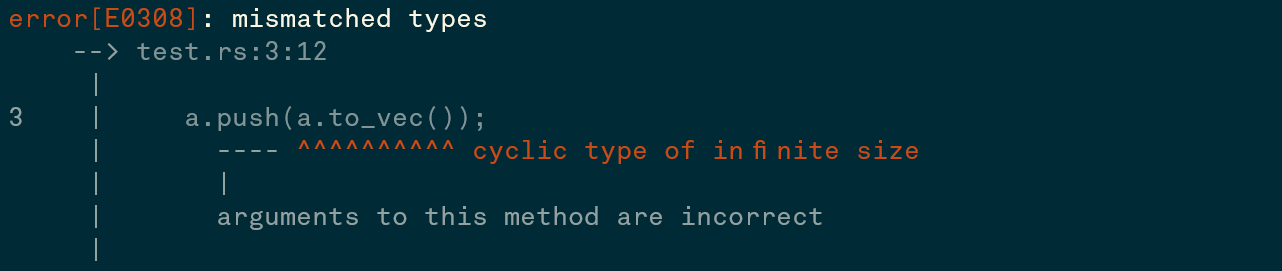
В данном примере generic в push - T, его значение равно типу a.to_vec(), то есть Vec<T>. Получаем T = Vec<T>. Единственное возможное решение для данного type constraint-а это: Vec<Vec<Vec<Vec<Vec<Vec<Vec<....>>>>>>>. Конечно есть языки которые это позволяют, но в данном случае для простоты и во избежании проблем, такие типы мы не будем принимать.
Реализуем occurs_in, который проверяет присутствует ли тип в generic аргументах другого если тот конструктор, или равен ему если он переменная:
impl TypeVariable {
fn occurs_in(&self, ty: Arc<Type>,
substitutions: &HashMap<TypeVariable, Arc<Type>>) -> bool {
match ty.as_ref() {
Type::Variable(v @ TypeVariable(i)) => {
if let Some(substitution) = substitutions.get(&v) {
if substitution.as_ref() != &Type::Variable(*v) {
return self.occurs_in(substitution.clone(), substitutions);
}
}
self.0 == *i
}
Type::Constructor(TypeConstructor { generics, .. }) => {
for generic in generics {
if self.occurs_in(generic.clone(), substitutions) {
return true;
}
}
false
}
}
}
}Также создадим функцию, которая будет рекурсивно проходится, по нашему хранилищу значений переменных типа, чтобы их полностью убрать, то есть например:
?1 = ?2
?2 = ?3
?3 = int
substitute(?1) = substitute(?2) = substitute(?3) = intimpl Type {
fn substitute(&self, substitutions: &HashMap<TypeVariable, Arc<Type>>) -> Arc<Type> {
match self {
Type::Constructor(TypeConstructor { name, generics }) => {
Arc::new(Type::Constructor(TypeConstructor {
name: name.clone(),
generics: generics
.iter()
.map(|t| t.substitute(substitutions))
.collect(),
}))
}
Type::Variable(TypeVariable(i)) => {
if let Some(t) = substitutions.get(&TypeVariable(*i)) {
t.substitute(substitutions)
} else {
Arc::new(self.clone())
}
}
}
}
}Мы это сделали, мы написали алгоритм унификации! Проверим его на практике! Помните предыдущий пример?
?3 = Array<?5>
?4 = int
?4 = ?1
?4 = int
?3 = Array<?6>
?6 = ?4
?3 = ?2Перед тем, как его симулировать, напишем два макроса:
Первый макрос, будет коротко генерировать переменную типа:
macro_rules! tvar {
($i:literal) => {
Arc::new(Type::Variable(TypeVariable($i)))
};
}Второй макрос, будет коротко генерировать конструктор типа:
macro_rules! tconst {
($name:literal,$($generic:expr)*) => {
Arc::new(Type::Constructor(TypeConstructor {
name: $name.to_owned(),
generics: vec![$($generic),*],
}))
};
($name:literal) => { tconst!($name,) };
}Теперь просимулируем наш предыдущий пример на нашей реализации алгоритма унификации:
fn main() {
let mut substitutions = HashMap::new();
unify(tvar!(3), tconst!("Array", tvar!(5)), &mut substitutions);
unify(tvar!(4), tconst!("int"), &mut substitutions);
unify(tvar!(4), tvar!(1), &mut substitutions);
unify(tvar!(4), tconst!("int"), &mut substitutions);
unify(tvar!(3), tconst!("Array", tvar!(6)), &mut substitutions);
unify(tvar!(6), tvar!(4), &mut substitutions);
unify(tvar!(3), tvar!(2), &mut substitutions);
for i in 1..=6 {
println!(
"{}: {:?}",
i,
Type::Variable(TypeVariable(i)).substitute(&substitutions)
);
}
}Получаем вывод:
1: Constructor(TypeConstructor { name: "int", generics: [] })
2: Constructor(TypeConstructor { name: "Array", generics: [Constructor(TypeConstructor { name: "int", generics: [] })] })
3: Constructor(TypeConstructor { name: "Array", generics: [Constructor(TypeConstructor { name: "int", generics: [] })] })
4: Constructor(TypeConstructor { name: "int", generics: [] })
5: Constructor(TypeConstructor { name: "int", generics: [] })
6: Constructor(TypeConstructor { name: "int", generics: [] })В следующей статье, мы начнем писать свой маленький язык программирования и начнем определять типы простых выражений таких как литералы или массивы!


Veritaris
Во втором примере описка
До вывода типов:
Сам вывод типов:
После подстановки тип
?2равенintвместоList<int>abs0luty Автор
Спасибо большое, за поправку!