Квантовые компьютеры. С точки зрения традиционного программиста-математика. Часть 1 / forpes.ru

Главная
Квантовые компьютеры. С точки зрения традиционного программиста-математика. Часть 1

Квантовые компьютеры. С точки зрения традиционного программиста-математика. Часть 1 +32

28.07.2023 08:37

java_prog 20 4100 Источник

О чем эта публикация

Имея более чем немалый опыт в традиционном программировании, я долгое время не касался темы квантовых компьютеров. Для меня это была какая то неизвестная магия. Безусловно, я знал теоретические основы, знал, какого рода задачи можно решать на квантовых цепях. Но не мог самостоятельно составить не только ни одной квантовой программы, даже разобраться в существующих квантовых алгоритмах не мог.

И вот, наконец, я закрыл этот пробел. И теперь, вспоминая, с каким непониманием я сталкивался, когда осваивал эту тему, захотел изложить ее так, чтобы тема была понятней с точки зрения опытного программиста. Конечно без математики тут никуда, нужно понимание линейной и комплексной алгебры. Поэтому, с точки зрения не просто программиста, а программиста-математика.

Многие теоретические курсы очень долго подводят к сути, накачивая нужной, но очень сложной теорией. Я попытался сократить этот период и как можно скорее перейти к сути, раскрывая нужную теорию по мере необходимости.

Квантовый регистр

В традиционных компьютерах память, это некоторый объем, допустим бит. Память имеет какое то состояние в момент времени, описываемое значением каждого бита. Также можно составить взаимно однозначное соответствие между состоянием памяти и числом от 0 до 2^n-1 . Например состояние памяти объемом 8 бит однозначно задается целым числом от 0 до 255. Эту память можно перевести из одного состояния в другое командой записи. А также можно в любой момент прочитать состояние памяти несколько раз, не изменяя её состояния.

В квантовых компьютерах свойства необычны. Квантовый регистр, который отдаленно можно назвать "памятью" может также иметь некоторый объем, допустим кубит.
На этом сходства заканчиваются.

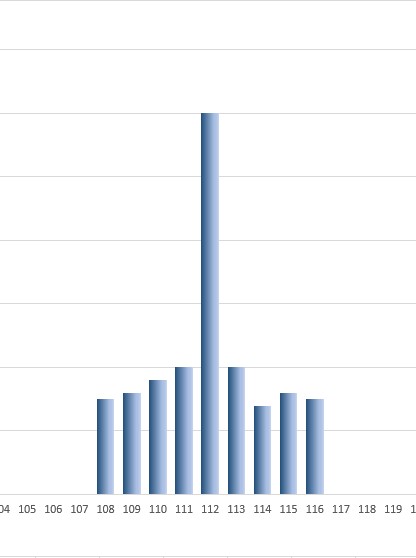
Состояние квантового регистра нельзя описать значением каждого кубита, как в традиционном случае. Квантовый регистр объемом 8 кубит, одновременно находится во всех традиционных состояниях от 0 до 255. Но с разными вероятностями. Какая то вероятность, что этот регистр равен 0, какая то вероятность, что этот регистр равен 127 или 255. Любое число от 0 до 255 с какой то вероятностью может быть в квантовом регистре. Обозначим набор этих вероятностей:

$\{p_0, p_1,\dots, p_{255}\}, \quad \sum_{j=0}^{255}p_j=1$

Распределение этих вероятностей и отражает состояние квантового регистра.

Состояние квантового регистра. Вероятно, в результате чтения такого регистра мы получим число 112, но можем получить и другие числа

Квантовый регистр можно переводить из одного состояния в другое. Но под состоянием, еще раз подчеркну, мы понимаем не текущее значение битов, как в традиционной памяти, а именно распределение вероятностей. То есть мы можем проводить операции, которые изменяют распределение вероятностей, $\{p_0, p_1,\dots, p_{255}\} \rightarrow \{p_0', p_1',...p'_{255}\}$ Состояние традиционного регистра памяти, получается, является частным случаем состояния квантового регистра. Действительно, допустим традиционный регистр памяти объемом 8 бит находится в состоянии 127. Но ведь можно описать это состояние и распределением вероятности, где все вероятности равны 0, кроме вероятности того, что регистр в состоянии 127.

$\{p_0=0, p_1=0,\dots , p_{127}=1,\dots , p_{255}=0\}$

Если происходит запись традиционного регистра и его новое значение, допустим 128, то эта операция в квантовом обобщенном виде будет выглядеть так:

$\{p_0=0, p_1=0,\dots , p_{127}=1,\dots , p_{255}=0\} \rightarrow \{p_0'=0, p_1'=0,\dots , p_{128}'=1,\dots , p_{255}'=0\}$

И последнее, это чтение. Прочитать квантовый регистр можно один раз за всё время его существования. Процедура чтения из квантового регистра из 8 кубит выдаст в результате какое-то одно любое значение от 0 до 255, для которого была ненулевая вероятность в состоянии на момент чтения регистра. После прочтения квантовый регистр уничтожается. Но это еще не самое неприятное. Самое неприятное, что состояние других регистров, которые мы не читали, после этой процедуры изменится. Необязательно читать весь квантовый регистр, можно читать отдельные его кубиты. В этом случае уничтожится часть кубитов квантового регистра и уменьшится объем квантового регистра, и конечно же самое неприятное - изменится состояние других, непрочитанных кубитов.

Занесем все изложенное в таблицу:

Традиционный регистр	Квантовый регистр
Имеет объем, измеряемый битами	Имеет объем, измеряемый кубитами
Состояние регистра, объемом бит задается числом от 0 до	Состояние регистра, объемом кубит задается распределением вероятностей $\{p_0, p_1,\dots, p_{2^n-1}\}, \sum_{j=0}^{2^n-1}p_j=1$
Состояние регистра объемом бит, можно изменять, записывая в него любое новое число от 0 до	Состояние регистра, объемом кубит можно изменить, в результате чего получится новое распределение вероятностей $\{p_0', p_1',\dots, p_{2^n-1}'\}, \sum_{j=0}^{2^n-1}p_j'=1$
Читать регистр объемом бит, можно сколько угодно раз не изменяя его состояния, в результате чтения получим число от 0 до , которое является состоянием регистра на момент чтения	Состояние регистра, объемом кубит можно прочесть всего один раз, уничтожив регистр, в результате чтения получим любое число от 0 до для которого в состоянии на момент чтения была ненулевая вероятность. Состояние остальных регистров в результате этой операции в общем случае изменяется

Кое-что формализуем, введем пару нотаций, терминов, и поедем дальше

Теперь можем крупными штрихами начертать, как выглядит программа для квантового компьютера. На вход программы подается квантовый регистр размера в каком-то состоянии, задаваемым распределением вероятностей $\{p_0, p_1,\dots, p_{2^n-1}\}, \sum_{j=0}^{2^n-1}p_j=1$

Далее этот регистр проходит через цепочку преобразований и чтений. Чтение в квантовых вычислениях называются - измерение. И далее я буду пользоваться этим термином. В процессе измерений, один или несколько кубитов регистра, что были измерены, будут уничтожены. В итоге на выходе программы мы получим квантовый регистр, того же, или другого размера , заданный состоянием $\{p_0', p_1',\dots, p_{2^m-1}'\}, \sum_{j=0}^{2^m-1}p_j'=1$

Далее полученный регистр может подаваться в другую квантовую программу, другую цепочку преобразований или может быть измерен, чтобы получить результат работы программы.

Вот мы и описали любую программу для квантового компьютера.

Пока всё понятно? Теперь повысим сложность изложения, скрепя сердце, но без этого дальше никак.

Во первых я сказал выше, что вероятности $\{p_0, p_1,\dots, p_{2^n-1}\}$ характеризуют состояние регистра. Но эти вероятности не описывают состояние квантового регистра однозначно. Квантовый регистр в разных состояниях может показывать одинаковое распределение вероятностей.

Но хорошая новость в том, что однозначное описание состояния квантового регистра не сильно отличается.

Однозначное описание состояния квантового регистра размера кубит задается комплексными числами $\{\alpha _0, \alpha _1,\dots, \alpha _{2^n-1}\}$ , такими, что вероятности равны:

$p_0=|\alpha_0|^2;\quad p_1=|\alpha_1|^2;\quad \dots p_{2^n-1}=|\alpha_{2^n-1}|^2$

Здесь, $|\alpha|^2$ это квадрат модуля комплексного числа. $|\alpha|^2=\alpha \alpha ^*$

Эти комплексные числа называются амплитуды состояния.

Очевидно, что могут существовать два различных комплексных числа $\alpha$ и $\beta\neq\alpha$ , что $|\alpha|^2=|\beta|^2$ . Поэтому описание состояния регистра с помощью вероятностей не является однозначным.

Далее введем следующую формальность. Будем иногда записывать состояние регистра вертикально

$\left( \begin{array}{cccc} \alpha_0\\ \alpha_1 \\ \vdots \\ \alpha_{2^n-1} \end{array} \right)$

Эта формальность облегчит нам математические преобразования состояния квантового регистра инструментами линейной алгебры.

Есть и другие нотации, обозначающие состояние квантового регистра. Если квантовый регистр состоит из одного кубита, его состояние можно обозначить, как

$\alpha_0 |0\rangle +\alpha_1 |1\rangle \quad (1)$

Напомню, что $p_0=|\alpha_0|^2$ это вероятность того, что в результате измерения этого кубита мы получим значение 0, $p_1=|\alpha_1|^2;\quad p_1=1-p_0$ - вероятность того, что в результате измерения этого кубита, мы получим значение 1.

Также справедливо следующее обозначение состояния регистра из нескольких кубит:

$\sum_j{\alpha_j |j\rangle}$

Иногда если, к примеру, у кубита $\alpha_0=1;\alpha_1=0$ , то со стопроцентной вероятностью в результате измерения мы получим значение 0. Тогда существует совсем краткое обозначение состояния кубита

$|0\rangle$

Что является частным случаем обозначения (1), при $\alpha_0=1;\alpha_1=0$

Наконец, никто не ограничивает нас использовать различные системы счисления, в этом случае, состояние регистра из двух кубитов могут записывать в двоичной системе, как

$\alpha_{00} |00\rangle +\alpha_{01} |01\rangle +\alpha_{10} |10\rangle +\alpha_{11} |11\rangle$

Квантовый компьютер позволяет преобразовывать состояние квантового регистра, изменяя состояние отдельных кубит, входящих в этот регистр и не трогая остальные. В классическом компьютере ведь тоже нет нужды переписывать всю память, если меняют только один-два байта в памяти. В этом случае кубит или кубиты, с которым идёт работа программы, могут быть записаны немного отдельно от остальных кубит и можно увидеть, например такие обозначения.

$\alpha_0\sum_j{\beta_j |j\rangle}\otimes|0\rangle +\alpha_1\sum_j{\beta_j |j\rangle}\otimes|1\rangle$

Здесь, интересующий нас кубит, может в результате измерения выдать 0 или 1 с вероятностями $p_0=|\alpha_0|^2,p_1=|\alpha_1|^2$ а состояние остальных кубитов регистра $\sum_j{\beta_j |j\rangle}$ нас по какой то причине не особо интересует.

Состояние нескольких кубитов

Допустим у нас есть два кубита, каждый со своим состоянием: $\alpha_0 |0\rangle +\alpha_1 |1\rangle$ и $\beta_0 |0\rangle +\beta_1 |1\rangle$

В каком состоянии будет система из двух кубит? Рассуждаем так: если нам надо посчитать вероятность того, что двукубитная система в результате измерения даст значение $|00\rangle$ , то нам надо взять вероятность того, что первый кубит в результате измерения даст значение $|0\rangle$ и одновременно второй кубит даст значение $|0\rangle$ .

Отсюда простое правило смешивания кубитов, чтобы получить совместное состояние нескольких кубитов, надо перемножить их состояния.

Данная формула и будет описывать состояние двухкубитного регистра, полученного из двух состояний двух кубитов

$\left( \begin{array}{cccc} \alpha_0\\ \alpha_1 \end{array} \right) \otimes \left( \begin{array}{cccc} \beta_0\\ \beta_1 \end{array} \right) = \left( \begin{array}{cccc} \alpha_0 \beta_0 \\ \alpha_0 \beta_1 \\ \alpha_1 \beta_0 \\ \alpha_1 \beta_1 \end{array} \right)$

Квантовая запутанность

Это одно из важнейших и очень загадочных свойств нашей вселенной, которому до сих пор не нашлось научного обоснования. И это свойство очень активно используется в квантовых вычислениях. Я бы даже сказал это самое главное свойство, без которого квантовые вычисления немыслимы.

Итак, допустим у нас есть квантовый регистр из двух кубитов в состоянии

$\alpha_0 |00\rangle +\alpha_1 |11\rangle$

То есть в этой системе исключены состояния $|10\rangle, |01\rangle$

Пусть мы берем один кубит из этих двух и измеряем. В процессе измерения получаем, к примеру значение 0. Измеренный кубит уничтожился. В каком состоянии находится оставшийся кубит?

Логика следующая, так как возможны были только состояния $|00\rangle, |11\rangle$ и мы в результате измерения выяснили, что один из кубитов дал значение 0, то система могла быть только в состоянии $|00\rangle$ , а значит второй кубит вероятно даст 0 в результате измерения. Но то логика, а что показывает реальная квантовая жизнь?

Реальная квантовая жизнь показывает абсолютно тоже самое. Почему тогда это удивительно?

Представьте такой эксперимент. Допустим мы построили такую систему из двух кубит и привели ее в состояние $\alpha_0 |00\rangle +\alpha_1 |11\rangle$ .

Затем один кубит был отправлен на Альфу-Центавра, второй остался на Земле. Если мы не будем измерять тот кубит, что остался на Земле, то измерение кубита на Альфа Центавре с некоторой вероятностью даст значение 0, с некоторой вероятностью даст значение 1. Но сразу как только мы измерим кубит на Земле и получим 1, то всё. Астронавты на Альфа-Центавра будут в результате измерения получат только 1 у своего кубита со стопроцентной вероятностью, никаких нулей там больше быть не может. Как эти кубиты общаются между собой на расстоянии световых лет друг от друга, как один из двух кубит "узнал", что второго кубита измерили? Это загадка вселенной. Замечу, что никакого парадокса с теорией относительности при этом не возникает. Вероятность это не информация и никакой информации мы не передаем, мы лишь можем обнаружить странные корреляции вероятностных событий на таких расстояниях, где они казалось бы, невозможны в виду невозможности вообразимой связи между этими событиями в течение малого промежутка времени.

А в наших квантовых вычислениях свойство квантовой запутанности используется очень активно. Как в примере выше, мы, измерив один из кубитов, перевели второй кубит в состояние, где стопроцентная вероятность получить предсказуемое значение в результате измерения. В общем случае измерение меняет состояние. В традиционном смысле, этот как если бы мы читали значение из памяти классической ЭВМ с одного адреса, а содержимое других адресов после операции чтения изменялось бы. С непривычки, квантовая спутанность кубитов может мешать нам. Например в классическом компьютере, если нет необходимости в каком то лишнем бите регистра, то мы можем не обращать на него внимания и спокойно работать с оставшимися битами.

В квантовом компьютере "выкинуть" в мусорку ненужный кубит нельзя. Ведь на мусорке какой нибудь злодей может измерить наш кубит, чем приведет нашу систему в совершенно не то состояние, которое мы хотим. Но, слава богу, программисты квантовых компьютеров научились правильно утилизировать ненужные кубиты, о чем я расскажу позже.

Если немного привыкнуть к свойству квантовой запутанности, то от него все таки больше пользы, чем вреда.

Посмотрим на задачу в общем случае. У нас была система из двух кубит в состоянии:

$\gamma_{00} |00\rangle +\gamma_{01} |01\rangle +\gamma_{10} |10\rangle +\gamma_{11} |11\rangle$

Мы измеряем первый (старший/левый) кубит из двух. Какова вероятность, что мы получим 0, какова вероятность что получим 1?

Тут всё просто, например, вероятность получить значение 0 это та же вероятность, что система из двух кубитов в результате измерения была бы $|00\rangle, |01\rangle$ то есть:

$P_0= |\gamma_{00}|^2+|\gamma_{01}|^2$ $P_1= |\gamma_{10}|^2+|\gamma_{11}|^2$

А теперь другой эксперимент, мы первым измеряем второй (младший/правый) кубит из двух, получаем 0. Какова теперь вероятность, что измерение первого кубита даст 0, какова вероятность 1?

Из за квантовой запутанности, так как второй кубит дал 0, то возможные состояния системы сокращаются до $|00\rangle$ или $|10\rangle$

Из начального состояния мы знаем, что вероятность первого события $|00\rangle$ до всех измерений была $|\gamma_{00}|^2$ , а вероятность второго события $|10\rangle$ была $|\gamma_{10}|^2$

Отношение этих вероятностей сохраняется после измерения, только теперь нам надо добавить нормировочный коэффициент, чтобы сумма вероятностей равнялась единице

$P_0= \frac{|\gamma_{00}|^2}{|\gamma_{00}|^2+|\gamma_{10}|^2}$ $P_1= \frac{|\gamma_{10}|^2}{|\gamma_{00}|^2+|\gamma_{10}|^2}$

Как видим, простое измерение одного из кубитов, изменило вероятности значений другого кубита, изменило состояние остальной части квантового регистра. Измеренный кубит был неотъемлемой частью состояния системы, и даже если нам он стал не нужен в процессе выполнения программы, пренебрегать им или отбрасывать нельзя.

Теперь предлагаю сделать перерыв в недельку, хорошенько уложить сказанное и приступать к следующей части: элементы квантовой программы: гейты.

Комментарии (20)

murkin-kot
28.07.2023 11:33
#25797502
+6
измерение кубита на Альфа Центавре

Нередко встречаюсь с подобной неграмотностью. Звезда, именуемая "Альфа Центавра", названа так по следующим причинам:

На небе (при наблюдении с земли) есть созвездия с устоявшимися названиями. Одно из них - созвездие кетнавра (или центавра на иностранный лад). В границах созвездия видны множество звёзд. Часть из них используется в качестве точек, связав которые, мы получаем изображение созвездия. Но большая часть звёзд в созвездии в связанную линиями фигуру не входят. Это база.

Проблема - нужно как-то уникально обозначить каждую звезду на небе.

Поскольку ранее (до изобретения телескопов) видимых звёзд было относительно немного, а сложные конструкции для измерения углов на небосводе были мало кому доступны, как-то устаканился очень простой метод идентификации, на основе принадлежности звезды к тому или иному созвездию. Находишь созвездие (без всяких инструментов), а потом уже намного меньшее количество звёзд мешает отысканию нужной.

Следствием предложенного способа стала проблема поиска звезды в границах созвездия. Но это уже совсем просто. Критерием сделали яркость свечения звезды. В результате получили упорядоченный по яркости список. Осталось только дать вторую координату (после идентификатора созвездия) в каком-то привычном большинству виде. Таким видом в итоге решили сделать буквенные идентификаторы из греческого алфавита. Соответственно, первой по яркости звезде в созвездии давали имя Альфа (да, это первая буква греческого алфавита). Последующим, соответственно, давали имена Бета, Гамма и т.д.

Теперь вам не составит труда найти на звёздном небе какую-нибудь Омикрон Водолея.

Но тема текста слегка другая - как же правильно назвать звезду первой величины в созвездии Кентавра? Какие окончания должны быть в получившемся названии?

Надеюсь, что теперь читатели легко разберутся, как правильно писать названия звёзд, ну а автор текста в дальнейшем не будет допускать таких очевидных ляпов.

ЗЫ. Автор, пиши исчо. Пишешь хорошо. Хоть иногда и пропускаешь важное, но уже по мелочи. А занудствую я не злобы ради, а математической точности для.

18741878
28.07.2023 11:33
#25797542
+1
https://www.piter.com/product/kvantovye-vychisleniya-dlya-nastoyaschih-aytishnikov
1. java_prog Автор
  28.07.2023 11:33
  #25798434
  Не читал, полистал. Написано неплохо и несколько более подробно, чем то изложение, что я запланировал. Рекомендую в качестве дополнительного или второго материала

ilriv
28.07.2023 11:33
#25798394
+3
Как эти кубиты общаются между собой на расстоянии световых лет друг от друга, как один из двух кубит "узнал", что второго кубита измерили? Это загадка вселенной

Они не общаются, они просто остаются частями единой системы. Тут больше актуален вопрос, почему эта единая система не разрушается и ее части продолжают взаимодействовать на расстоянии. Формальный ответ: потому что [общая] функция состояния этих частиц не зависит от расстояния между ними. А почему не зависит?
1. zaiats_2k
  28.07.2023 11:33
  #25799212
  +5
  Потому что у запутанных частиц есть прямые ссылки друг на друга. Оптимизация такая, все ж равно эта запутанность распадается быстро если не предпринимать титанических усилий для её сохранения. Разработчики видимо решили пренебречь вероятностью появления ученых, которые станут этим злоупотреблять. Или оставили там где-то TODO и забыли.

iShrimp
28.07.2023 11:33
#25798796
В общем: система из n кубитов находится одновременно в 2^n состояниях (каждое состояние имеет свой вес) до тех пор, пока мы её не трогаем. Но стоит нам измерить любой кубит, как система вместе с нами и всем окружающим миром делится на две несовместимые ветви: в одной из них будут те состояния, в которых кубит равен 0, а в другой - те состояния, в которых он равен 1. Причём для нас, как наблюдателя, вероятность оказаться в мире, где кубит равен 0, равна сумме весов всех подходящих (совместимых) состояний. Все неподходящие будут автоматически "отброшены".

Измерив все кубиты, мы в итоге получим какое-то одно из состояний с некоей вероятностью. Если нас интересует общая картина их распределения, то мы можем много раз повторить весь цикл работы квантового компьютера и в итоге накопить статистику.

EvilMan
28.07.2023 11:33
#25799456
+3
https://vas3k.blog/blog/quantum_computing/ - как мне кажется, вот тут неплохое введение в тему Квантовых вычислений для начала формирования бэкграунда.
1. java_prog Автор
  28.07.2023 11:33
  #25800072
  Да, неплохо. По стилю мне напомнило книги Айсберга, если помните "Радио это просто" и т.д. с Знайкиным и Незнайкиным.

sshmakov
28.07.2023 11:33
#25799520
Предположим, что кое-кто, не будем уточнять кто, но по злому умыслу, взял и подменил нам два наших кубита до их разделения обычными кубиками, на одном из которых выгравирована единица, а на втором ноль. Этот кое-кто сам уж не помнит, кому какой кубик остался, поэтому с вероятностью 50% на Земле кубик с нулем, и 50% с единицей. Суперпозиция, ага.

Так вот, пробуем мы на Земле открыть коробочку и измерить наш кубит, а на самом деле измеряем кубик, но не знаем об этом. Опа, а там нолик. Ага, а значиться наши товарищи, долетевшие до Альфы, значиться, Центавра, измеряют свой кубик, а там, вы не поверите, как раз единица образовалась. Такая, понимаешь, загогулина.

И вот что интересно, судари мои, что если бы мы измерили свой кубик, но получили единицу, то вот те товарищи с Центавра получили бы не единицу, а шиш с маслом, то есть нолик, нес па?

Как же это они на своей Альфе узнают, что у нас получается и делают всё напротив нас?
1. java_prog Автор
  28.07.2023 11:33
  #25800140
  +1
  Вы подходите с позиции супер-детерминизма .
  
  Но, как вы понимаете, не вам одному приходила эта идея.
  
  Кубит можно не только тупо вскрыть и узнать его значение, но и предварительно сделать какие то преобразования, а потом подсмотреть. Со спутанным кубитом можно также преварительно провести некоторые преобразования и подсмотреть. И как бы вы не пытались объяснить результат с позиции детерминированности, всегда можно подобрать такие предварительные преобразования перед измерением кубитов, что на множестве экспериментов статистический результат измерений будет отличаться от того, что должен был бы быть при ваших объяснениях с позиции супер-детерминизма.
  
  Если хотите, я могу в следующей части попытаться изложить https://ru.wikipedia.org/wiki/Неравенства_Белла упрощенным и понятным образом на паре примеров.
  1. sshmakov
    28.07.2023 11:33
    #25800198
    Смысл моего комментария в том, что пример с двумя кубитами слабоват для объяснения квантовой запутанности и того, насколько это круто. Но для начала объяснения пойдет, конечно.
    
    Не берусь указывать вам, какую тему раскрывать в следующей части - на ваше усмотрение. Пишете вы хорошо, понятно, спасибо за статью.
    
    Vytian
    28.07.2023 11:33
    #25800432
    Автор несколько раз подчеркнул, что информация, которая измеряется, это даже не вероятность, а амплитуда вероятности. Вы в контрпримере прячете этот факт под словом "забыл". То есть судить, верно ли считан кубик нельзя, ведь его исходное состояние забыто, то есть передачи информации нет. Вы конечно можете верить, можете не верить в то, что вы когда-то знали исходное состояние, и что это такой хитрый план. Но эксперимент Алана Аспе говорит об обратном.
    
    sshmakov
    28.07.2023 11:33
    #25800566
    Не увидел в статье про Алана Аспе. Наверное, позже будет.
    
    А кубитам можно задать заранее известные амплитуды вероятностей? Ну, чтобы знать исходное состояние?

3263927
28.07.2023 11:33
#25800194
спасибо! очень интересно, если бы поменьше формул но подробнее простым языком то было бы проще наверное воспринимать... или хотябы пояснения под формулами. а так супер вроде понятно

Yukr
28.07.2023 11:33
#25800480
Ох уж эта квантовая запутанность.... что-то тут не так, не зря физики не могут её объяснить. Может перемудрили, и нет её?

Ну вот в одном из объяснений о запутанности приводят пример с перчатками: если на Альфу Центавра увезли одну из перчаток, то посмотрев на оставшуюся (например -левую), можно однозначно понять, что увезли правую. А вся запутанность состоит в том, что мы изготовили/ назвали перчатки левая и правая.
1. ilriv
  28.07.2023 11:33
  #25800680
  С перчаткой это абсолютно неправильная аналогия.
  
  Если вы знаете что в Восточном полушарии сейчас день, значит в Западном полушарии - ночь. И наоборот. Чтобы в двух полушариях был день, пришлось бы разрубить планету на две части и развернуть оба полушария к Солнцу.
  
  Точно так же со связанными частицами.
  
  Квантовая запутанность это простое следствие из запрета Паули ("связанные" частицы, которые находятся в в одной квантовой системе, не могут иметь одинаковое физическое состояние). Нам непонятна только причина, почему связанные частицы сохраняют связь даже когда мы разводим их друг от друга на какое-то расстояние. Хотя с другой стороны, почему бы нет?
  
  То есть непонятно, почему состояние связанности не зависит от расстояния.
  1. Yukr
    28.07.2023 11:33
    #25800798
    +1
    Не соглашусь.
    
    Перчатки выходят с завода попарно, сшитые из одного куска материала.
    
    Запутаные частицы тоже "изготавливаются" одновременно, в ходе облучения лазером кокого-либо нелинейного кристалла. на выходе имеем различно парно поляризованые частицы.
    
    вот иллюстрация процесса : https://upload.wikimedia.org/wikipedia/commons/7/75/SPDC_figure_RU.png
    
    Т.е. одновременность и один источник получения может быть причиной "запутанности".
    
    Вот если бы взяли 2 частицы от разных лазеров, да повернули им спин поляризаторами, одному влево, другому вправо, разнесли их на 1000 км, а потом, определив спин одного, точно узнали бы спин другого - вот это бы была истинная запутанность. Нет?
    
    ilriv
    28.07.2023 11:33
    #25800916
    Запутанные частицы не обязательно "изготавливаются" одновременно, они могут существовать как самостоятельные частицы до момента запутывания. Например когда атом поглощает электрон, электрон становится часть квантовой системы, т.е. запутывается с другими частицами этого атома. А до поглощения электрон не является запутанным.
    
    Запутанность появляется в тот момент, когда на частицу начинает действовать запрет Паули. Она снимается, когда запрет Паули прекращает действовать.
    
    Zenitchik
    28.07.2023 11:33
    #25803740
    А откуда мы знаем, что до и после момента запутывания это те же самые частицы? Может, они слились в виртуальную частицу, которая потом распалась на пару новых частиц?

Yukr
28.07.2023 11:33
#25801430
Спасибо, не знал. В любом случае, тема интересная, хочется разобраться. Если окажется, что вывернув левую перчатку наизнанку на Земле, обнаружится, что правая на Альфе Центавра тоже вывернулась, это будет прямо фантастика.

Квантовые компьютеры. С точки зрения традиционного программиста-математика. Часть 1 +32

О чем эта публикация

Квантовый регистр

Кое-что формализуем, введем пару нотаций, терминов, и поедем дальше

Состояние нескольких кубитов

Квантовая запутанность

Комментарии (20)

java_prog Автор

java_prog Автор

java_prog Автор