17.10.2023 08:39
java_prog 0 1100 Источник

В прошлой части мы рассмотрели, как выглядят квантовые цепи с традиционными логическими операциями над данными. Сегодня мы рассмотрим два классических квантовых алгоритма, которые дают существенный выигрыш в производительности по сравнению с классическими алгоритмами решения этих задач.

Рассмотрим квантовую цепь с функцией f(x) которая принимает на вход n-разрядный параметр x и в качестве результата выдает всего один бит 0 или 1.

Я обозначил знаком \oplus логическую операцию xor - исключающее ИЛИ. Мне надоело писать XOR, с символом \oplus все выглядит компактнее и нагляднее. К тому же таким символом эта операция традиционно обозначается в литературе по квантовым вычислениям. Не путайте с операцией \otimes, которую мы используем для тензорного произведения квантовых состояний.

Итак, для такой квантовой цепи, которая реализует эту функцию f(x) нам пришлось кроме аргумента добавить на вход еще один кубит b. Зачем нам пришлось это сделать рассмотрено в прошлой части. На выходе у нас повторяется аргумент функции x и результат функции f(x) с маской исключающего или кубита b,\quad f(x)\oplus b

Используем параллелизм, подаем на вход это цепи суперпозицию всех возможных состояний разрядности n

\sum_{x=0}^{2^n-1}\alpha_x|x\rangle

В этом случае на выходе из данной цепи мы получим повтор аргумента и результат с маской "исключающего или" входящего кубита b

\sum_{x=0}^{2^n-1}\alpha_x|x\rangle\otimes |b\oplus f(x)\rangle

И здесь у нас есть несколько приемов, чтобы обработать результат этого параллелизма. Самый очевидный, это подать на вход b состояние |0\rangle

В этом случае, операция b\oplus f(x)=0\oplus f(x)=f(x) и мы получим все возможные состояния, дополненные на результат функции f(x)

\sum_{x=0}^{2^n-1}\alpha_x|x\rangle\otimes |f(x)\rangle

Но распространен также прием, который мы использовали в прошлой части: на вход b подают состояние |0\rangle -|1\rangle тогда состояние:

|b\oplus f(x)\rangle

разбивается на суперпозицию двух возможных состояний кубита b

|0\oplus f(x)\rangle -|1\oplus f(x)\rangle

Далее используем тот математический факт, что 0\oplus f(x)=f(x),\quad 1\oplus f(x)=\neg f(x)
получаем в итоге:

|b\oplus f(x)\rangle=|f(x)\rangle -|\neg f(x)\rangle

Так как функция f(x) имеет результат размером всего в один бит, то нам достаточно рассмотреть два случая f(x)=0,f(x)=1

В первом случае

|b\oplus f(x)\rangle=|0\rangle -|1\rangle

Во втором случае

|b\oplus f(x)\rangle=|1\rangle -|0\rangle=-(|0\rangle -|1\rangle)

Или, если этот минус изобразить в виде (-1)^{f(x)} то можно записать общее выражение, охватывающее оба случая

|b\oplus f(x)\rangle=-(-1)^{f(x)}(|0\rangle -|1\rangle)

И наконец, с учетом повтора состояния x на выходе

|b\rangle\otimes\sum_{x=0}^{2^n-1}\alpha_x|x\rangle\xrightarrow{f}\sum_{x=0}^{2^n-1}(-1)^{f(x)}\alpha _x|x\rangle\otimes(|0\rangle -|1\rangle)

То есть в результате такого находчивого приема мы получаем на выходе для тех x для которых f(x)=0 получаем состояние с положительным знаком. А для тех состояний, для которых f(x)=1 получаем состояние с отрицательным знаком.

Этим приемом мы воспользовались в прошлой части, когда решали задачу с черным ящиком. Но прием можно применить и в других задачах. Вот мы и рассмотрим один из таких алгоритмов - алгоритм Дойча-Йожи.

Алгоритм Дойча-Йожи

Один из первых квантовых алгоритмов. Задача поставлена следующим образом. Есть некоторая функция - черный ящик. На вход принимает n-разрядное двоичное число. На выходе скрытая функция черного ящика выдает результат размером всего один бит.

В зависимости от некоторого скрытого параметра черного ящика, данная функция либо выдает результатом одно и то же значение для любого аргумента. Либо ровно для половины всех аргументов функция выдает результатом 1, а для второй половины аргументов результатом будет 0.

И нам нужно установить - какой тип черного ящика перед нами. Тот который выдает константу для всех значений, или тот который выдает два разных бита.

С классическим алгоритмом все элементарно. Нам надо взять и направить в черный ящик минимум 2^{n-1}+1 различных значений. Если для всех значений результатом будет один и тот же бит, то у нас очевидно константный черный ящик. Если результатами будут разные биты, то это второй тип черного ящика, что выдает разные результаты для ровно половины аргументов.

По теории вероятностей, для больших n в случае второго типа ящика нам потребуется перебрать гораздо меньше значений, чем 2^{n-1}+1, прежде чем мы обнаружим различные результаты и, таким образом, сможем утверждать, что это второй тип ящика.

Аналогично в случае, если мы получили несколько константных результатов, то с очень высокой вероятностью перед нами ящик первого типа - константный. Но это только вероятностный ответ. Если мы хотим получить ответ с вероятностью 1, то нам надо подать на вход 2^{n-1}+1 значений.

Другое дело квантовый алгоритм. Допустим мы воспользуемся приемом, описанным выше. Тогда у нас будет суперпозиция всех состояний от |0\rangle\quad до\quad |2^n-1\rangle

При этом те аргументы, для которых скрытая функция черного ящика возвращает 0 будут со знаком +, для которых скрытая функция черного ящика возвращает 0 будут со знаком -. Что это нам дает?

Рассмотрим первый случай, если это функция константная, то все состояния будут с одинаковым знаком, либо все с плюсом, либо все с минусом.

\pm\sum_{x=0}^{2^n-1}{|x\rangle }

Такое состояние можно получить если подать на вход n-кубитного гейта Адамара состояние

\pm |00\dots 000\rangle

А значит, если мы на выходе квантовой цепи поставим еще один гейт Адамара, то благодаря обратимости, мы получим исходное состояние.

\pm\sum_{x=0}^{2^n-1}{|x\rangle }\xrightarrow{H^{(n)}}\pm |00\dots 000\rangle

Если мы измерим этот результат, то очевидно мы получим результат 00\dots 000 с вероятностью 1.

Рассмотрим второй случай, функция черного ящика не константная и выдает для половины всех аргументов 0, а для остальных аргументов 1.

В этом случае, после применения приема выше, мы получим суперпозицию состояний с разными знаками. Ровно половина знаков будет +, ровно половина знаков будет -.

\sum_{x=0}^{2^n-1}{\pm |x\rangle }

Что будет если мы подадим такое состояние в гейт Адамара?

Вспоминаем формулу для гейта Адамара разрядности n

H^{(n)}|y\rangle=\frac{1}{2^\frac{n}{2}}\sum_{j=0}^{2^n-1}{(-1)^{p(j \land y)} |j\rangle}

но мы не будем вычислять все амплитуды, а просто немного разобьем данную сумму на две части, нас интересует итоговая амплитуда у состояния |0\rangle:

H^{(n)}|y\rangle=\frac{1}{2^\frac{n}{2}}|0\rangle+\frac{1}{2^\frac{n}{2}}\sum_{j=1}^{2^n-1}{(-1)^{p(j \land y)} |j\rangle}

И получаем, что для состояния +|x\rangle

H^{(n)}|x\rangle=\frac{1}{2^\frac{n}{2}}|0\rangle+...

а для состояния -|x\rangle

H^{(n)}-|x\rangle=-\frac{1}{2^\frac{n}{2}}|0\rangle+...

Ну и наконец, если мы подаем на вход гейта Адамара суперпозицию таких состояний

H^{(n)} \sum_{x=0}^{2^n-1}{\pm |x\rangle }=\sum_{x=0}^{2^n-1}{\pm \frac{1}{2^\frac{n}{2}}|0\rangle }+...

Ну и , наконец, вспоминаем, что ровно половина аргументов дает 0 и ровно другая половина аргументов дает 1. Значит

\sum_{x=0}^{2^n-1}{\pm \frac{1}{2^\frac{n}{2}}|0\rangle } =0

Ведь ровно половина результатов будет с плюсом и ровно половина с минусом.

И значит вероятность при измерении результата получить результатом 00\dots 000 будет 0. Мы получим какое угодно значение, но только не ноль.

И в этом и состоит суть алгоритма. Если мы получаем в результате измерения нули по всем разрядам, то это константный черный ящик. Если получаем в результате измерения ненулевое значение, то это ящик, в котором половина аргументов дает 0, а другая половина дает 1.

Приведем полную квантовую цепь для алгоритма Дойча-Йожи. Она ничем не отличается от схемы, что мы использовали в прошлой задаче, только другой черный ящик и другая интерпретация результатов.

Задача Саймона

Тема непростая, все никак не мог зайти на эту задачу с каким то простым объяснением. Вот, что в итоге получилось.

Итак, сначала сама задача с примерами.

У нас есть некоторый черный ящик. Этому черному ящику мы скармливаем произвольное число x разрядности n бит. Результатом работы черного ящика является число y=f(x) также разрядностью n бит. Сам результат не так важен, главное свойство черного ящика состоит в следующем:

f(x)=f(x\oplus s)

Где s это скрытый, ненулевой параметр черного ящика, который необходимо найти. Символом \oplus мы чуть выше договорились обозначать логическую операцию xor - исключающее ИЛИ.

Ну, и понятно, что для всех остальных аргументов, значение черного ящика уникально

f(x_1)\neq f(x_2)\quad если x_1\neq x_2\quad и x_1\neq x_2\oplus s

Разберем конкретный пример. Допустим, параметр трехразрядного черного ящика, который нам нужно отыскать равен 101_b

Для каких значений черный ящик будет возвращать одинаковые результаты. По условию задачи, это пары, x, x\oplus s=x\oplus 101_b Составим список всех таких пар, их всего должно быть четыре пары.

000_b, 000_b\oplus 101_b=101_b 001_b, 001_b\oplus 101_b=100_b 010_b, 010_b\oplus 101_b=111_b 011_b, 011_b\oplus 101_b=110_b

Для таких пар наш черный ящик должен выдавать одинаковый уникальный результат. В остальном наш черный ящик ничем не ограничен. Например, черный ящик может работать вот так:

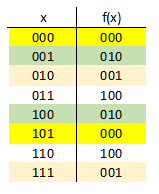
Но это мы пока только разобрались с тем, как работает черный ящик. А теперь разберемся с задачей Саймона: имея такой черный ящик, найти скрытый параметр s обратившись к ящику минимальное число раз.

Как решить задачу на традиционном компьютере? Очевидно, нам нужно "скармливать" черному ящику различные аргументы, пока у нас не возникнет хотя бы одного совпадения результатов черного ящика. Допустим в задаче выше мы перебираем просто все аргументы подряд. Тогда первая пара с одинаковым результатом у нас будет на пятой итерации f(001_b)=f(100_b)=010_b Далее, имея эту пару мы уже легко можем вычислить s=001_b\oplus 100_b=101_b и исходная задача решена.

Вся сложность только в том, сколько итераций нам в среднем понадобиться, чтобы найти хотя бы один совпадающий результат черного ящика. По теории вероятностей ("Парадокс дней рождений") нам потребуется число операций примерно равное \sqrt{2^n}=2^{n/2} В самом худшем случае нам придется перебрать половину значений 2^{n-1} прежде, чем мы найдем пару.

Но это классический алгоритм решения. Теперь попытаемся решить задачу квантовой цепью.

Как обычно, воспользуемся параллелизмом. С помощью гейта Адамара получим равновероятное состояние всех возможных аргументов черного ящика и "скормим" их черному ящику.

Получим таким образом, как и в прошлых задачах суперпозицию всех состояний x спутанные с результатами работы черного ящика f(x). Как обычно, мы опускаем нормировочный коэффициент для упрощения выражения. Состояния равновероятны и коэффициент одинаков, его всегда можем вернуть

\sum_x{|x\rangle\otimes|f(x)\rangle }

Если мы распишем наш случай трехразрядного черного ящика из цветастого примера выше, то это будет такое состояние:

|000\rangle\otimes|000\rangle+|001\rangle\otimes|010\rangle+|010\rangle\otimes|001\rangle+|011\rangle\otimes|100\rangle+ |100\rangle\otimes|010\rangle+|101\rangle\otimes|000\rangle+|110\rangle\otimes|100\rangle+|111\rangle\otimes|001\rangle

И далее мы легко можем получить из этого состояние суперпозицию где будет только искомая пара, для которых f(x) возвращает одинаковое значение. Действительно, просто измерим этот регистр f(x), как обозначено на схеме. Даже не важно, что мы получим. Ну, допустим, как в примере выше, мы получим 100_b. Как мы учились ранее, просто вычеркиваем из исходного до измерения состояния все компоненты, где f(x)\neq 100_b

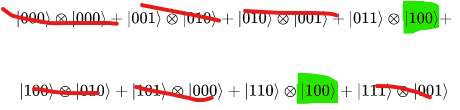
То есть, в результате измерения мы получим состояние

|011\rangle+|110\rangle

То есть мы сразу за одну итерацию получаем одну из нужных нам пар, ради которой в классическом случае нам пришлось бы перебрать в среднем 2^{n/2} итераций. Теперь осталось найти s=011_b\oplus 110_b

В общем случае мы получим состояние

|r\rangle+|r\oplus s\rangle

где r,r\oplus s это случайная пара, для которой черный ящик выдает одинаковые значения.
Но, не торопитесь радоваться. То что казалось простым на классическом компьютере, теперь оказалось тяжелейшей задачей для квантового компьютера. Имея состояние |011\rangle+|110\rangle мы не можем с этим что-то сделать квантовыми цепями, чтобы получить 011_b\oplus 110_b

И большую часть решения задачи Саймона составляет эта, казалось бы тривиальная, часть. Но программисты решили ее следующим образом.

Данное состояние |r\rangle+|r\oplus s\rangle подают в гейт Адамара. Что получится в итоге?

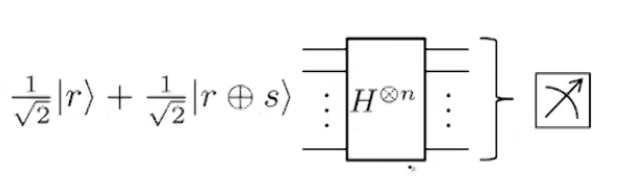
Вспоминаем нашу формулу для гейта Адамара

H^{(n)}|y\rangle=\frac{1}{2^\frac{n}{2}}\sum_{x=0}^{2^n-1}{(-1)^{p(x \land y)} |x\rangle}

Опустим для простоты нормировочный коэффициент \frac{1}{2^\frac{n}{2}} подставим в эту формулу наше состояние

H^{(n)}(|r\rangle+|r\oplus s\rangle)=\sum_{x=0}^{2^n-1}{((-1)^{p(x \land r)}+(-1)^{p(x \land (r\oplus s))}) |x\rangle}

Воспользуемся формулой для побитовых логических операций, которые легко проверить:

x\land (r\oplus s)=(x\land r) \oplus (x\land s)

И второе, что также легко проверить, это свойство исключающего или

p(a\oplus b)\mod 2=(p(a)+p(b))\mod 2

Тогда можно вынести за скобки (-1)^{p(x \land r)} и останется

=\sum_{x=0}^{2^n-1}(-1)^{p(x \land r)}(1+(-1)^{p(x \land s)}) |x\rangle

Отсюда видно, что если в числе x\land s нечетное количество ненулевых бит, то (-1)^{p(x\land s)}=-1 и значит выражение в скобках будет равно нулю. А значит если мы измерим этот результат после гейта Адамара, то в результате такого измерения мы никак не сможем получить такое x, что x\land s содержит нечетное количество бит в двоичной записи.

Мы перебираем в сумме все возможные значения x от 0 до 2^n-1, а значит x\land s ровно для половины 2^{n-1} всех возможных значений x даст четное количество бит, а для другой половины - нечетное количество бит. И если мы измерим теперь этот результат, то в результате измерения мы получим какое-то случайное число x, одно из 2^{n-1} возможных, такое, что x\land s имеет в двоичной записи четное количество бит.

Если мы обозначим x_m - бит с номером m в двоичной записи числа, то можем переписать это выражение следующим образом

x_0\cdot s_0+x_1\cdot s_1+\ldots+x_{n-1}\cdot s_{n-1} \mod 2 =0

Это уравнение по модулю 2, где каждое число это один бит: 0 или 1.

Нам нужно найти s, а значит в этом уравнении нам неизвестны s_0,s_1,\ldots,s_{n-1}

Но известны, полученные в результате измерения x_0,x_1,\ldots,x_{n-1}

Но этого мало. Уравнение с n неизвестными, а занчит нам нужно, как минимум n-1 линенйно независимых уравнений, чтобы решить эту систему.

Поэтому нам понадобятся еще итерации с черным ящиком, чтобы получить какое то другое x.
Вернемся для иллюстрации к нашему "цветному" примеру черного ящика с s=101_b
Какие существуют x, чтобы x\land s имел четное количество бит в двоичной записи?

Их существует всего четыре: 000_b,010_b,101_b,111_b ровно половина из возможных трехразрядных значений. Чтобы найти три неизвестных, нам надо как минимум два линейно независимых уравнения.

И вот, собрали мы такую квантовую цепь и сделали первый замер. Получили любое случайно из четырех значений, например 101. Потом сделали второй замер и получили, к примеру 111. Смогли составить систему уравнений:

1\cdot s_0+0\cdot s_1+1\cdot s_2\mod 2=0 1\cdot s_0+1\cdot s_1+1\cdot s_2\mod 2=0

Теперь решаем эту систему. от второго уравнения отнимаем первое и получаем, что s1=0
И остается уравнение s_0+s_2\mod 2=0 у которого возможны два решения: s_0=s2=0, s0=s2=1

То есть у нас получились два решения системы: s=000_b, s=101_b

По условию черного ящика s - ненулевой параметр, поэтому первое решение отбрасываем. И получаем ответ s=101_b Ровно тот параметр, что скрывал от нас черный ящик.

Мы всегда в такой системе имеем одно из решений s=0, поэтому нам и потребовалось всего n-1 линейно независимых уравнений.

В общем случае нам надо сделать как минимум n-1 итерацию, чтобы получить n-1 линейно независимых уравнений для вычисления битов s.

Нам может не повезти и мы получим x=0, либо тоже самое значение x, что получали на прошлой итерации. Если нам повезёт, то мы выберем из всех 2^{n-1} всех возможных значений x какое то новое значение, которого не было ранее.Также нам может не повезти если вдруг получится значение x, которое является линейно зависимым от других, ранее полученных значений x.

Не будем сейчас делать вычисления теории вероятности, чтобы совсем не усложнять эту тему. Теория вероятности уже за нас все подчитала и вычислила, что для получения линейно независимой системы уравнений нам потребутеся обратится к черному ящику в среднем линейное от n число раз для достаточно больших n.

Несмотря на необходимость решать систему уравнений, это существенная оптимизация по сравнению с классическим алгоритмом, которому требовалось в среднем 2^{n/2} итераций.

Комментарии (0)