В прошлой части мы рассмотрели двухкубитные гейты и построили какие то элементарные программы на двухкубитных гейтах. Разберем некоторые полезные программы, которые состоят из двух или более разъединенных удаленных друг от друга частей, связанных между собой только предварительно запутанными кубитами и классическими средствами связи: телефоном, телеграфом, бумажным письмом и т.п. Например, один запутанный кубит отправляется на Луну, другой остается на Земле. Основной результат действия таких программ заключается в том, что предварительно запутанные кубиты, разделенные расстоянием, участвуют во взаимодействии с другими независимыми кубитами (взятыми уже на месте - на Луне и Земле), запутывая их в свою очередь, что в итоге такого взаимодействия получается общая связанная запутанная система, несмотря на разделенность расстоянием.

Удаленное запутывание

Программа ниже действует также, как и CNOT, только может выполнятся на некотором расстоянии в пространстве, передавая нужные данные для операции по любым другим "классическим" каналам связи: письмо телефон и так далее.

Как это принято в компьютерной литературе, у нас будут сегодня на площадке знаменитые Алиса и Боб.

Алиса и Боб предварительно получили равновероятное запутанное состояние двух кубитов: . Мы уже легко научились получать такие состояния, поэтому не будем останавливаться на том, как такое состояние было получено. Для простоты повествования опустим множитель , мы вернем нужный множитель по окончании всей процедуры, когда пронормируем ответ. Итак, запишем изначальное равновероятное спутанное состояние двух кубитов так:

Пусть жёлтый кубит остается у Алисы, а зеленый кубит Боб забирает с собой и улетает на Луну. После этого Боб и Алиса выполняют следующую программу:

Если быть точнее, то это две программы: одну выполняет Алиса на Земле, используя свой жёлтый кубит, другую выполняет Боб на Луне, используя свой зеленый кубит.

Что получится в результате выполнения программы? Давайте проведем пошаговую отладку.
Так как у нас запутанные кубиты, мы не можем рассматривать состояние регистров по отдельности и должны рассматривать совокупное состояние всех трех кубитов: желтого, зеленого и дополнительного произвольного кубита который Алиса использует на входе своей части программы и который мы не будем красить, оставим бесцветным. Запишем это совокупное состояние:

Раскроем скобки, выполнив все перемножения:

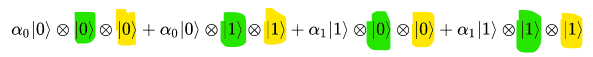
Далее Алиса, находясь на Земле использует гейт CNOT над своими двумя кубитами: бесцветный кубит она использует в качестве управляющего, а жёлтый кубит в качестве управляемого. Как мы помним, гейт CNOT инвертирует управляемый кубит, если на управляющем входе 1, и не изменяет управляемый кубит, если на управляющем входе 0. Тогда, чтобы получить результат воздействия CNOT нам надо везде, где бесцветный кубит равен , инвертировать жёлтый кубит, и ничего не менять там, где бесцветный кубит равен . Получается после гейта CNOT следующее состояние:

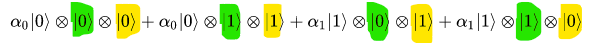
Далее, Алиса измеряет свой жёлтый кубит. В итоге она может получить два состояния 0 или 1. Любой из этих результатов приведёт нашу систему в новое состояние.

• Если в результате измерения вышло 0, то вычеркиваем все слагаемые, где желтый кубит был равен , как мы уже научились делать ранее:

  

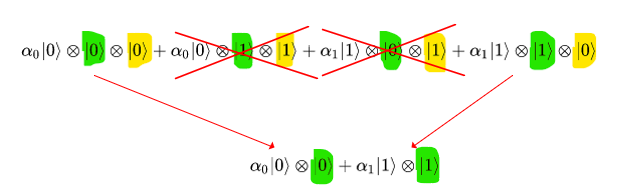
• Если в результате измерения вышло 1, то вычеркиваем все слагаемые, где желтый кубит был равен :

  

  Далее Алиса берёт в руки телефон, телеграф или любое другое классическое средство связи и звонит Бобу на Луну, сообщая результат своего измерения 0 или 1. На схеме такое общение представлено пунктирной линией. Если Алиса сообщает, что у нее измерение дало 0, то Боб не делает ничего. Если Алиса сообщает, что у нее измерение дало 1, то Боб пропускает свой зеленый кубит через гейт-инвертор (гейт NOT). В первом случае, где Боб ничего не делает, система остается в состоянии:

  

  Во втором случае, мы инвертируем зелёный кубит, принадлежащий Бобу, и получаем тот же результат

  

  На этом, конец. Это и будет конечное состояние работы программы. А теперь заметим, что точно такой же результат мы получали в прошлой части, когда рассматривали эту схему:

  

  Но теперь подобная схема может работать удаленно, что открывает нам новые возможности.

Квантовая телепортация

Помните в прошлой части, мы сделали схему, которая ничего полезного не делала:

Но теперь, когда мы научились делать удалённый CNOT, давайте разрежем эту схему на две части. Одну часть будет выполнять Алиса на Земле, вторую часть будет выполнять Боб на Луне:

Это та же самая схема, только CNOT заменён на удалённый CNOT, работу которого мы разобрали выше. Краткое содержание схемы: Алиса и Боб имели начальное равновероятное спутанное состояние двух кубитов:

Жёлтый кубит остается у Алисы, а зеленый кубит Боб забирает с собой и улетает на Луну. После приземления Алиса берёт абсолютно любой, произвольный кубит в произвольном состоянии , и выполняет удалённый CNOT, используя этот произвольный кубит и свой жёлтый кубит. Результат измерения, Алиса сообщает Бобу по телефону. Информация, которую она сообщает имеет размер всего в один классический бит. Боб, используя эту информацию, применяет или не применяет гейт инвертирования над своим зелёным кубитом. Алиса применяет над своим оставшимся кубитом (желтый кубит был уничтожен в результате измерения) гейт Адамара, после чего измеряется результат. Результат Алиса сообщает Бобу по телефону, размер этой информации также один классический бит. Боб на Луне, в зависимости от результата, что он получил по телефону, использует над своим зеленым кубитом гейт инверсии фазы. После этой процедуры у Боба остается зеленый кубит в состоянии , а у Алисы все кубиты уничтожены.

В чем красота? Алиса взяла абсолютно любой произвольный кубит, а в результате работы программы кубит в абсолютно таком же состоянии оказался у Боба. Телепортировался. и это произвольные (с учетом нормировки), да еще и комплексные числа. В два бита их не упаковать. Но Алиса сообщила Бобу всего два классических бита информации по телефону и никаким другим образом не взаимодействовала с Бобом. Боб на своей стороне получил точно такое же состояние, с точно такими же комплексными амплитудами, используя всего два бита информации. Похоже на фокус. И это есть фокус, который до сих пор является загадкой нашей вселенной. Одно из проявлений квантовой запутанности. По какому каналу вселенная сообщила кубиту Боба, какое состояние ему надо принять? Фокус вселенной. Но двух битов на это явно мало.

Отмечу, что данная программа это уже не теория, она осуществлена на практике. Экспериментальная реализация квантовой телепортации поляризационного состояния фотона была осуществлена в 1997 году почти одновременно группами физиков под руководством Антона Цайлингера (Университет Инсбрука) и Франческо де Мартини (Университет Рима) С тех пор многие группы ученых проводили эксперименты по квантовой телепортации, постоянно совершенствуя технику.

Главная проблема запутанных состояний состоит в следующем: в теории мы можем говорить, что Боб берет свой кубит и летит на Луну. А на практике любая квантовая частица находится в запутанном состоянии пока с чем-нибудь не взаимодействует. Иначе, как мы видим, получаются новые запутывания и новые состояния. И перенести кубит даже на метр, чтобы в него не влетела какая-то другая частица или он не подвергся электромагнитному излучению, крайне и крайне сложно. Но каждый эксперимент по квантовой телепортации все более и более совершенствуется. В июне 2017 года китайские учёные осуществили квантовую телепортацию на расстояние свыше 1200 километров.

Запрет клонирования

Напрашивается вопрос. Если мы можем телепортировать точную копию кубита на произвольное состояние, используя всего два бита информации, переданной по классическим каналам, то нельзя ли написать программу, которая создаст точную копию состояния на другом кубите, не уничтожая исходный кубит. В традиционном компьютере ведь мы легко копируем и клонируем тонны информации.

В квантовом компьютере такое сделать невозможно. Желающие могут почитать доказательство этой невозможности, но если нет желания, то придется поверить без доказательств. Клонировать произвольное состояние кубита нельзя. Но можно создать сколь угодно близкое состояние с произвольной точностью.

Симуляция онлайн

Один из читателей порекомендовал симулятор квантового компьютера онлайн. Я особо не тестировал, но на первый взгляд выглядит вполне достойно для онлайн инструментов. К тому же обозначения гейтов вполне соответствует тем, что я давал в прошлых частях.

Вот, например, разобранная выше программа квантовой телепортации.

Прилагается инструкция и видеоурок на английском, а разбирающимся, есть исходный код симулятора.