Квантовые компьютеры. С точки зрения традиционного программиста-математика. Часть 3 / forpes.ru

Главная
Квантовые компьютеры. С точки зрения традиционного программиста-математика. Часть 3

Квантовые компьютеры. С точки зрения традиционного программиста-математика. Часть 3 +11

11.08.2023 07:18

java_prog 3 1200 Источник

В прошлой части мы рассмотрели однокубитные гейты и построили какие то элементарные программы на однокубитных гейтах. Пришло время перейти к многокубитным преобразованиям.

Квантовые гейты в случае многокубитных операций

Можно также рассмотреть каждый гейт с точки зрения матрицы преобразования. Но такое описание слишком громоздко. Например состояние из двух кубит:

$\alpha_{00} |00\rangle + \alpha_{01} |01\rangle + \alpha_{10} |10\rangle + \alpha_{11} |11\rangle$

Требует матрицы размера 4х4 для преобразования одного состояния в другое

$\left( 4х4 \right) \left( \begin{array}{cccc} \alpha_{00} \\ \alpha_{01} \\ \alpha_{10} \\ \alpha_{11} \end{array} \right) = \left( \begin{array}{cccc} \alpha_{00} \\ \alpha_{01} \\ \alpha_{10} \\ \alpha_{11} \end{array} \right)$

И далее все нарастает экспоненциально, преобразование трехкубитного состояния требует матрицы 8х8 и так далее.

Поэтому, чаще многокубитные гейты описывается аналитическими правилами: каким правилом должны преобразовываться одно состояние в другое, либо как можно вычислить любой элемент матрицы преобразования любого размера.

Рассмотрим самые важные и частоиспользуемые гейты.

Гейт CNOT

Двухкубитный гейт,

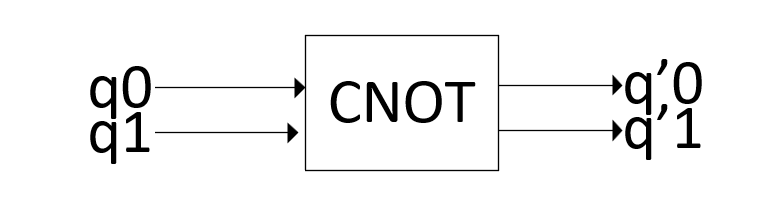
Который чаще рисуют в следующем виде:

Верхний кубит называют "управляющим", второй кубит называют "управляемым". Смысл гейта следующий:

управляющий кубит проходит без изменений,
управляемый кубит инвертруется, если управляющий кубит в состоянии $|1\rangle$ , либо остается без изменений, если управляющий кубит в состоянии $|0\rangle$

По сути для управляемого кубита это кубит NOT, который включается только если на управляющем кубите 1, и выключен в остальных случаях.

Если задать данное преобразование формулой, то это будет:

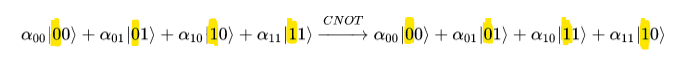
Здесь управляющий кубит обозначен желтым маркером. Как видно из формулы, там где управляющий кубит был 0 - ничего не изменилось. Там, где управляющие кубит был 1, состояние управляемого бита инвертировано. Можно традиционно обозначить преобразование, используя матрицу 4 на 4. Такая матрица будет выглядеть так:

$\left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{array} \right) \left( \begin{array}{cccc} \alpha_{00} \\ \alpha_{01} \\ \alpha_{10} \\ \alpha_{11} \end{array} \right) = \left( \begin{array}{cccc} \alpha_{00} \\ \alpha_{01} \\ \alpha_{11} \\ \alpha_{10} \end{array} \right)$

Не знаю какое описание из приведенных примеров вам более понятно и близко, но надеюсь, я сумел донести, как действует гейт CNOT.

Данный гейт используют для разных целей, одно из частых использований, это создание запутанных состояний. Например, разберем действие следующей программы для квантового компьютера:

На управляющий вход гейта подается произвольный кубит в любом произвольном состояни $\alpha_0 |0\rangle + \alpha_{1} |1\rangle$ На управляемый вход подается кубит $|0\rangle$ то есть, другими словами кубит в состоянии $1\cdot |0\rangle + 0\cdot |1\rangle$ Что будет на выходе? Можем решать эту задачу любым удобным способом, например решим ее так. Запишем совместное состояние двух кубитов на входе, где выделим управляющий кубит желтым маркером:

Далее, мы инвертируем управляемый кубит там, где управляющий кубит был равен 1.

Теперь выкинем из ответа те состояния, где амплитуда 0 и остается

$\alpha_0 |00\rangle +\alpha_1 |11\rangle$

А мы знаем по прошлым частям, что такое состояние, это состояние квантовой запутанности. Если мы теперь измерим любой из кубитов и получим, к примеру 0, то после этого второй кубит будет показывать в результате измерения 0 с вероятностью 100%.
Теперь мы научились программно получать такие запутанные состояния с помощью гейта CNOT.
А теперь вспомним о том, что гейты обладают свойством обратимости и применим гейт CNOT к результату повторно. Не будем повторять все выкладки достаточно прочитать все что было раньше в обратном порядке. В итоге мы с помощью этого гейта "распутаем" квантовую запутанность и получим снова два независимых кубита, один из которых в состоянии $|0\rangle$ а другой кубит в состоянии $\alpha_0 |0\rangle + \alpha_{1} |1\rangle$

Задача 1

Построить программу, где на вход подаются два кубита в состояни $|00\rangle$ , а на выходе - запутанное состояние двух кубитов, где состояния $|00\rangle , |11\rangle$ равновероятны.

Выше, мы уже получали запутанное состояние, используя гейт CNOT:

$\alpha_0 |00\rangle +\alpha_1 |11\rangle$

Чтобы состояния были равновероятны, достаточно будет выполнения условия:

$\alpha_0=\alpha_1$

При этом должно быть выполнено условие нормировки, чтобы общая вероятность любого состояния равнялась единице

$|\alpha_0|^2+|\alpha_1|^2=1$

Данная система тривиальна и дает решение:

$\alpha_0=\alpha_1= \frac{1}{\sqrt{2}}$

То есть по условию задачи, нам нужно получить состояние:

$\frac{1}{\sqrt{2}} |00\rangle +\frac{1}{\sqrt{2}} |11\rangle$

Нам нужно получить такое состояние из двух кубитов, каждый из которых в состоянии $|0\rangle$ .
Чтобы получить такое состояние, используя гейт CNOT, нам надо на управляемый вход подать кубит в состоянии $|0\rangle$ . Здесь ничего делать не надо.
А вот на управляющий кубит нам надо подать состояние

$\frac{1}{\sqrt{2}} |0\rangle +\frac{1}{\sqrt{2}} |1\rangle$

И вопрос, как получить такое состояние из $|0\rangle$ ?
Если вы не забыли прошлую часть, то такое преобразование можно сделать, используя гейт Адамара.
Таким образом, общая схема программы, решения задачи выглядит так:

Схема получения равновероятных запутанных состояний

Задача 2

Разобрать работу следующей программы:

Два кубита, один в состоянии $|0\rangle$ , другой в состоянии $\alpha_0 |0\rangle + \alpha_{1} |1\rangle$ Кубиты проходят через гейт CNOT, как мы уже знаем, после этого гейта образуется запутанное состояние:

$\alpha_0 |00\rangle +\alpha_1 |11\rangle$

Далее один из кубитов поступает в гейт Адамара, после чего измеряется. Измерение обозначается на схемах в виде такой пиктограммы стрелочного прибора. В процессе измерения измеряемый кубит уничтожается. В каком состоянии окажется второй кубит в итоге работы данной программы?
С гейтом CNOT все уже понятно и разобрано, "отлаживаем" далее программу слева направо.
Какое состояние получится после гейта Адамара можно вычислить двумя способами, разберём оба:
1-ый способ. Запишем состояние кубита, который поступает в гейт Адамара в виде вектора. Одним компонентом вектора будет множитель, что у кубита при состоянии $|0\rangle$ , а вторым компонентом будет множитель при состоянии $|1\rangle$ . Второй кубит в преобразовании Адамара не участвует, но его состояния также являются частями вектора.

$\alpha_0 |00\rangle +\alpha_1 |11\rangle \rightarrow \left( \begin{array}{cccc} \alpha_0 |0\rangle \\ \alpha_1 |1\rangle \end{array} \right)$

Далее умножим матрицу, которая соответствует преобразованию Адамара, на этот вектор

$\frac{1}{\sqrt{2}}\left( \begin{array}{cccc} 1 & 1 \\ 1 & -1\end{array} \right) \left( \begin{array}{cccc} \alpha_0 |0\rangle \\ \alpha_1 |1\rangle \end{array} \right)=\frac{1}{\sqrt{2}}\left( \begin{array}{cccc} \alpha_0|0\rangle+\alpha_1|1\rangle \\ \alpha_0|0\rangle-\alpha_1|1\rangle \end{array} \right)$

И далее мы возвращаем этот вектор в привычный вид, приписывая к одному компоненту вектора состояние $|0\rangle$ , а ко второму компоненту вектора состояние $|1\rangle$

$\frac{1}{\sqrt{2}}|0\rangle\otimes(\alpha_0|0\rangle+\alpha_1|1\rangle) +\frac{1}{\sqrt{2}}|1\rangle\otimes(\alpha_0|0\rangle-\alpha_1|1\rangle)\quad(1)$

Можем раскрыть скобки, тогда получится

$\frac{1}{\sqrt{2}}(\alpha_0|00\rangle+\alpha_1|01\rangle+\alpha_0|10\rangle-\alpha_1|11\rangle)$

Это и будет нашим состоянием после применения гейта Адамара.
2-ой способ. Более аналитический, зато не требует матриц.
Аналитически применение преобразование Адамара описывают так: кубит к которому применяется преобразование заменятся по следующему правилу:

$|0\rangle\xrightarrow{H}\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)$ $|1\rangle\xrightarrow{H}\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)$

Попробуем применить это правило к нашему спутанному состоянию. На этот раз не будем красить желтым, просто отметим, что гейт Адамара применяется к левому старшему кубиту состояния:

Применяем правила преобразования Адамара к левому кубиту:

$|0\rangle \otimes \alpha_0|0 \rangle+|1\rangle\otimes\alpha_1|1\rangle\xrightarrow{H} \frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)\otimes \alpha_0|0\rangle+\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)\otimes\alpha_1|1\rangle=$ $= \frac{1}{\sqrt{2}}(\alpha_0|00\rangle+\alpha_1|01\rangle+\alpha_0|10\rangle-\alpha_1|11\rangle)$

Приходим к тому же результату, что и в способе 1.
Теперь последнее действие программы - измерение левого старшего кубита.
Чтобы нагляднее увидеть результат, удобнее пользоваться формулой (1)
Если в процессе измерения кубита получился 0, то "вычеркиваем" из состояния те старшие кубиты, что были в состоянии 1, по оставшемуся кубиту остается состояние

$\alpha_0|0\rangle+\alpha_1|1\rangle$

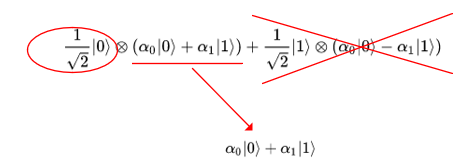
Вычеркиваем состояние 1, так как процесс измерения дал 0

Если в процессе измерения кубита получился 1, то "вычеркиваем" из состояния те старшие кубиты, что были в состоянии 0, по оставшемуся кубиту остается схожее состояние, но с другой фазой

$\alpha_0|0\rangle-\alpha_1|1\rangle$

Задача 2 решена, но попробуем продолжить построение цепи следующим образом: Допустим в конце цепи из задачи 2 сидит программист и действует следующим образом:

если в результате измерения был 0, то программист ничего не делает
если в результате измерения был 1, то программист к оставшемуся кубиту применяет однокубитный гейт "Инверсия фазы". Обозначим эту схему следующим способом.

Здесь после измерительного прибора, в зависимости от результата измерения работает, либо не работает еще один гейт "Инверсия фазы". Если в результате измерения был 1, то оставшийся кубит был в состоянии $\alpha_0|0\rangle-\alpha_1|1\rangle$ . Применяем к нему гейт инверсии фазы, получаем $\alpha_0|0\rangle+\alpha_1|1\rangle$ А это ровно такое же результат какой у нас получался в случае, если бы результатом измерения был 0. Поэтому объединим эти результаты и запишем следующей схемой:

Данную программу назовем программой переноса состояния. Обратите внимание, кубит в произвольном состоянии $\alpha_0|0\rangle+\alpha_1|1\rangle$ поступал на верхний вход программы, а вышел из нижнего. Казалось бы, такая программа не имеет никакого практического смысла. Поступил кубит в произвольном состоянии, и мы очень сложным способом добились того, чтобы получить то же самое, что было на входе. И не ждите подвоха, это правда. Действительно программа не имеет никакого практического смысла. Мы на ней попрактиковались в отладке программ и гейтов. И далее мы еще кое что в ней поменяем, что придаст в новой программе некоторый смысл.

Двухкубитный гейт Адамара

По сути, двухкубитный гейт Адамара, это два гейта Адамара в одной коробке, каждый независимо воздействет на свой кубит.

Давайте попробуем вычислить какие состояния будут получаться у двухкубитного Адамара для состояний: $|00\rangle, |01\rangle, |10\rangle, |11\rangle$ и попробуем построить матрицу 4х4 такого гейта.

начнем с состояния $|00\rangle$ . Тут все просто, по свойству однокубитного гейта Адамара каждый однокубитный $|0\rangle$ превращается в состояние с равновероятными $|0\rangle, |1\rangle$

$|00\rangle\xrightarrow{H}\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle) \otimes\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)$ $=\frac{1}{2}(|00\rangle+|01\rangle+|10\rangle+|11\rangle)\quad(2)$

состояние $|01\rangle$ . Тут тоже не сложно, по свойству однокубитного гейта Адамара каждый однокубитный $|0\rangle$ превращается в состояние с равновероятными $|0\rangle, |1\rangle$ , а каждый однокубитный $|1\rangle$ превращается в состояние с равновероятными $|0\rangle, |1\rangle$ где фаза у состояния $|1\rangle$ отрицательная, то есть амплитуда это состояния с минусом.

$|01\rangle\xrightarrow{H}\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)\otimes\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)$ $= \frac{1}{2}(|00\rangle-|01\rangle+|10\rangle-|11\rangle)\quad(3)$

состояние $|10\rangle$ . Почти не отличается от прошлого случая, просто знаки меняются в других местах.

$|10\rangle\xrightarrow{H}\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)\otimes\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)$ $=\frac{1}{2}(|00\rangle+|01\rangle -|10\rangle - |11\rangle)\quad(4)$

состояние $|11\rangle$ .

$|11\rangle\xrightarrow{H}\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)\otimes\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)$ $= \frac{1}{2}(|00\rangle-|01\rangle-|10\rangle+|11\rangle)\quad(5)$

Теперь попробуем вычислить, какая матрица будет у двухкубитного гейта Адамара. Вспомним что каждому двух кубитному состоянию, соответствует какой то вектор в 4-х мерном пространстве.

$\alpha_{00} |00\rangle + \alpha_{01} |01\rangle + \alpha_{10} |10\rangle + \alpha_{11} |11\rangle\equiv\left( \begin{array}{cccc} \alpha_{00} \\ \alpha_{01} \\ \alpha_{10} \\ \alpha_{11} \end{array} \right)$

Отсюда получается, что

$|00\rangle\equiv\left( \begin{array}{cccc} 1 \\ 0 \\ 0 \\ 0 \end{array} \right), |01\rangle\equiv\left( \begin{array}{cccc} 0 \\ 1 \\ 0 \\ 0 \end{array} \right),$ $|10\rangle\equiv\left( \begin{array}{cccc} 0 \\ 0 \\ 1 \\ 0 \end{array} \right), |11\rangle\equiv\left( \begin{array}{cccc} 0 \\ 0 \\ 0 \\ 1 \end{array} \right)$

Теперь переходим к поиску матрицы. Запишем выражение (2) в векторно-матричном виде

$\left(\begin{array}{cccc} H \end{array} \right)\left( \begin{array}{cccc} 1 \\ 0 \\ 0 \\ 0 \end{array} \right)=\frac{1}{2}\times\left(\begin{array}{cccc} 1 \\ 1 \\ 1 \\ 1 \end{array}\right)$

А значит, правый вектор и будет первой вертикальной колонкой искомой матрицы. Аналогично из выражений (3),(4),(5) получаем остальные вертикальные колонки, и, наконец, запишем всю матрицу двухкубитного гейта Адамара:

$\frac{1}{2}\times \left( \begin{array}{cccc} 1 & 1 & 1 & 1 \\ 1 & -1 & 1 & -1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 \end{array} \right)$

Учитываем, что все многокубитные гейты Адамара строятся сходным образом - каждый входящий кубит проходит через однокубитный гейт. Попробуйте самостоятельно вычислить общий случай, как будет выглядеть n-кубитный гейт Адамара, для n больших, чем 2.

Комментарии (3)

vlad1953
11.08.2023 16:10
#25850114
+1
Автор действительно хорошо пишет именно про квантовые вычисления. Таких подробных статей почти нет в русском сегменте интернета. Возможно, только на сайте http://www.eslitak.com/ можно найти что-то подобное. Автор, пиши, пожалуйста, дальше.
1. java_prog Автор
  11.08.2023 16:10
  #25850370
  +1
  Спасибо. Такие отзывы дают новую энергию для работы над новыми статьями

NightShad0w
11.08.2023 16:10
#25850396
Спасибо за труд! С удовольствием читаю.

Квантовые компьютеры. С точки зрения традиционного программиста-математика. Часть 3 +11

Квантовые гейты в случае многокубитных операций

Гейт CNOT

Задача 1

Задача 2

Двухкубитный гейт Адамара

Комментарии (3)

vlad1953

java_prog Автор

NightShad0w