Нейронные сети, графы и эмерджентность / forpes.ru

Главная
Нейронные сети, графы и эмерджентность

Нейронные сети, графы и эмерджентность +27

30.07.2023 14:27

DeadPhilosopher 30 3500 Источник

В этой статье я хочу попробовать осветить некоторые интересные, на мой взгляд, области науки, с которыми я сталкивался в контексте работы с нейронными сетями, и найти между ними взаимосвязь. Данная статья не претендует на истину в последней инстанции и является всего лишь попыткой посмотреть на нейронные сети под другим углом. Сразу предупреждаю - я не являюсь каким то глубоким специалистом в этих сферах.

Нейронные сети

Нейронные сети сейчас - крайне активно развивающаяся сфера, в которой каждый день происходит новая научная революция, появляются новые архитектуры, фундаментально меняющие всю область и быстро имплементируемые в реальные продукты. Однако для этой, относительно новой области, все еще существует ряд крайне важных проблем, методы решения которых сейчас, с моей точки зрения, оставляют желать лучшего.

Одна из интереснейших проблем сейчас заключается в том, что новые архитектуры - это по сути, рукомахательно придуманные лайфхаки. Посмотрим на конкретные примеры:

YoloR: You Only Learn One Representation: Unified Network for Multiple Tasks

Архитектура YoloR, основная магия заключается в implicit knowledge блоке

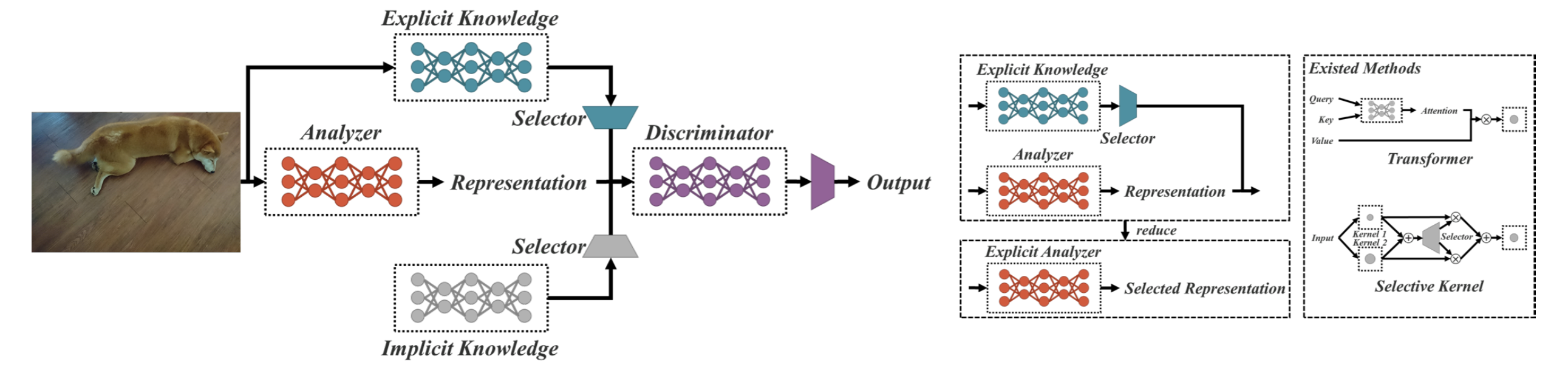
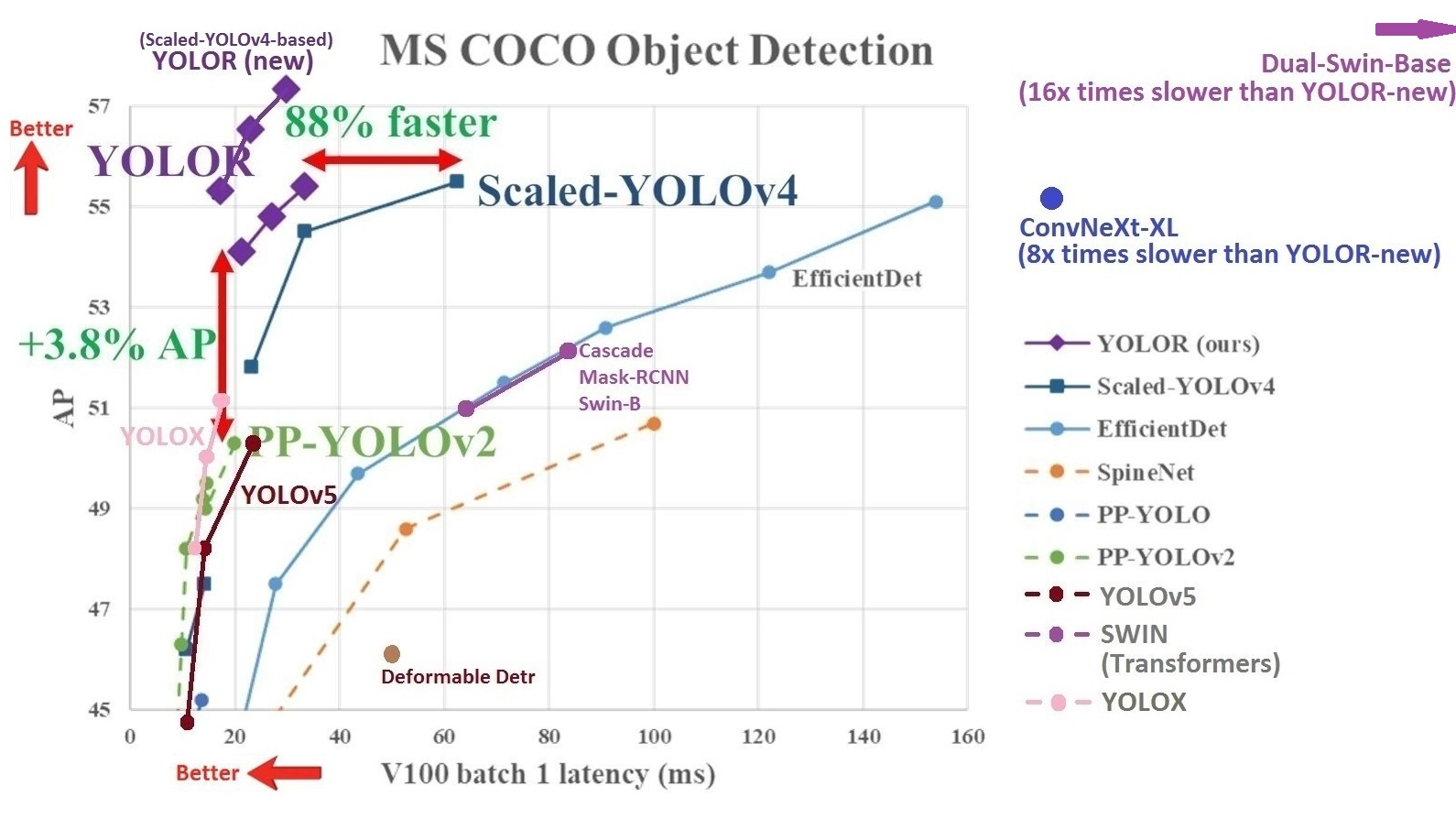
Данная сеть, на датасете COCO, в рамках задачи детектирования, превосходит большинство своих конкурентов по ряду параметров (во всяком случае, превосходила на момент выхода).

Однако, если вы решитесь прочитать саму статью о данной модели, то будет серьезнейший риск не понять, о чем вообще речь и что происходит в данной нейронной сети. Все дело в том, что магия этой архитектуры заключается в добавлении блока без входа - implicit knowledge блока, в который стекаются данные "независящие от входа", т.е. некоторое неявное представление знаний.
Что это означает с формальной точки зрения? Не представляю.

Attention Is All You Need

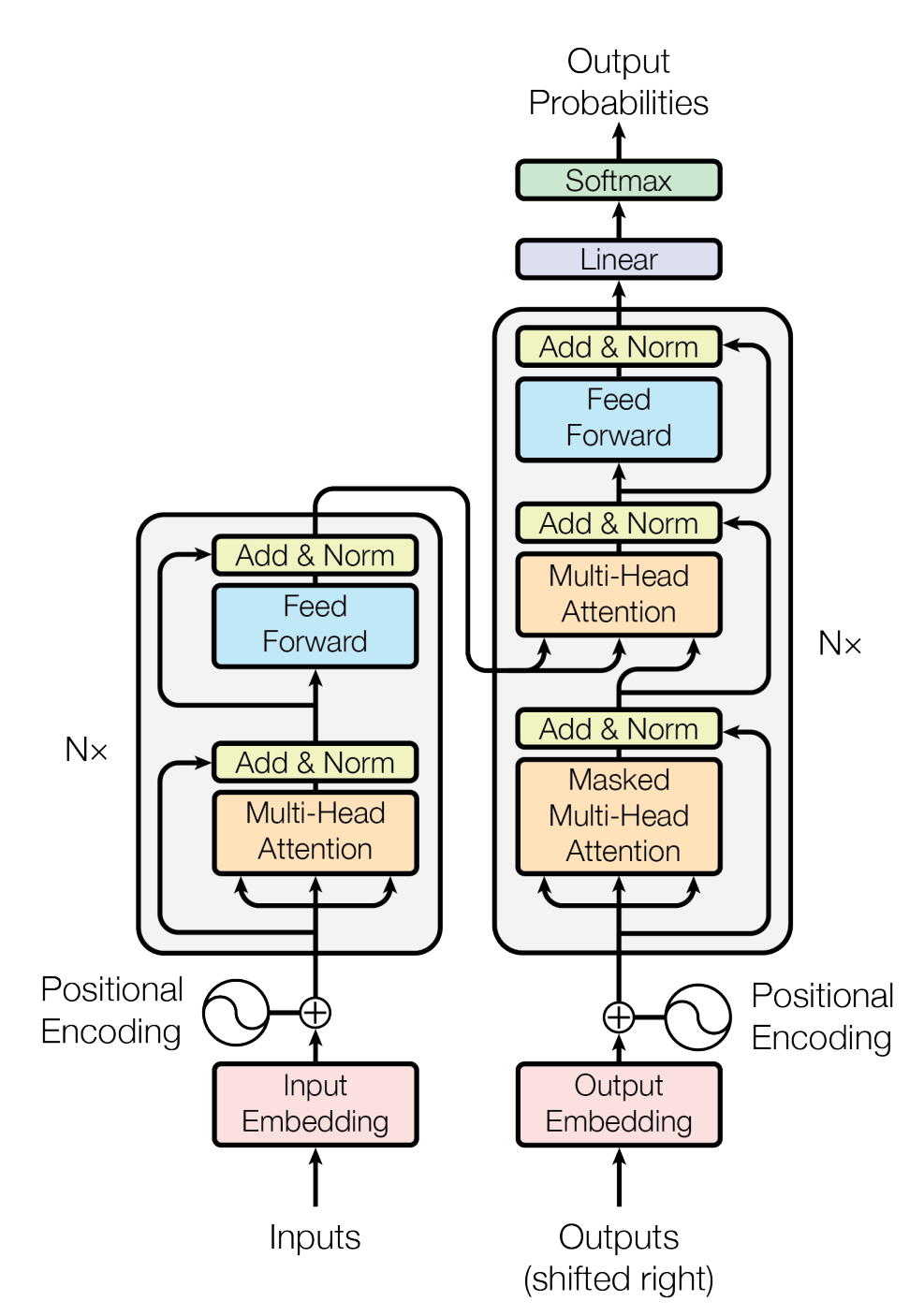
Но может, предыдущий пример бы не удачным? Обратимся к тому, что у всех на слуху: Трансформеры.
Начало данной, без преувеличения, прорывной архитектуры было положено в статье с сильным заголовком "Attention Is All You Need".

Основная идея статьи, как следует из названия, заключается в том, что добавление multi-head attention позволяет превосходить практически любые другие архитектуры.

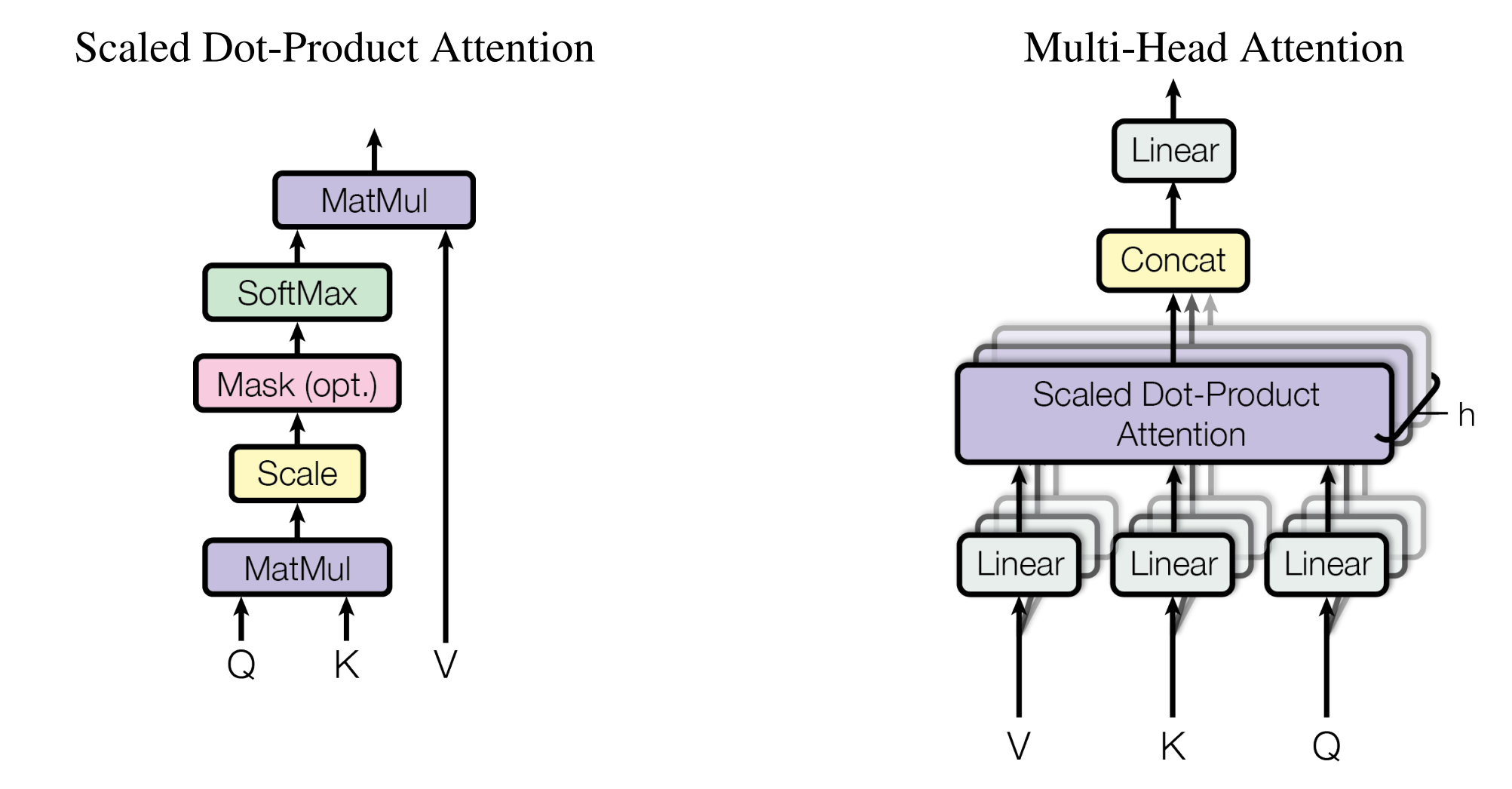
И это касается не только обработки текстов - трансформеры так же прекрасно справляются с обработкой изображений (SWIN). Объясняется это в основном тем, что multi-head attention блок можно воспринимать, как нелинейную функцию нового типа. Вкупе с большим числом параллельных потоков данных - это дает значительный прирост в эффективности нейронной сети.
Звучит убедительно? Так в чем же проблема?
А в том, что, что архитектура на чистом multi-head attention не просто плоха - она не будет работать:
Attention is Not All You Need: Pure Attention Loses Rank Doubly Exponentially with Depth

Авторы другой статью пошли еще дальше и полностью убрали self-attention из своей сети. Результатом стала архитектура:
MLP-Mixer: An all-MLP Architecture for Vision

MLP-Mixer, по сути представляет собой ViT без attention

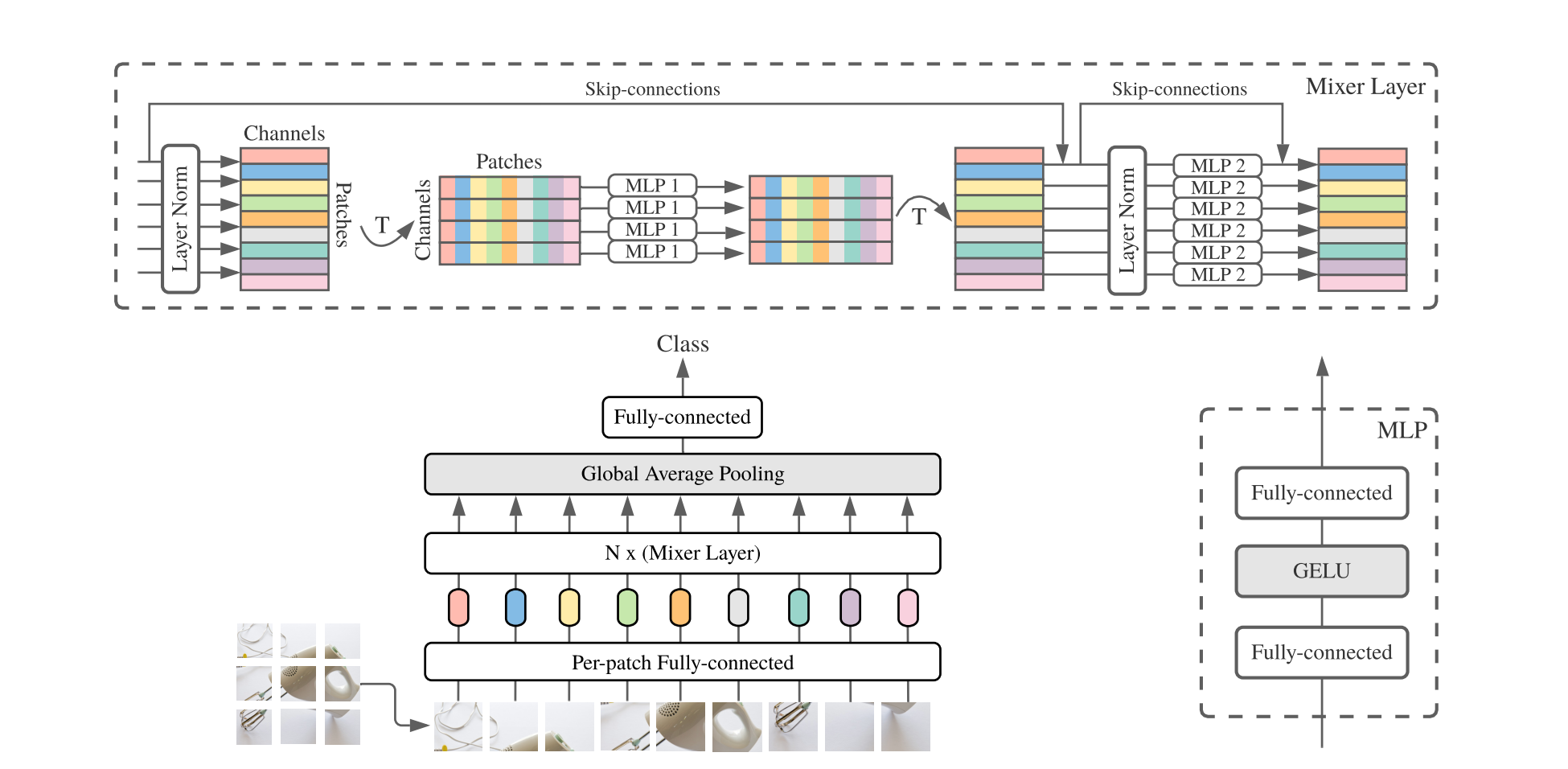
В котором все self-attention были заменены на обычные MLP слои. И при сравнении с аналогичными transformer-base сетями оказалось, что при значимом росте скорости работы, сеть практически не теряет в качестве:

Сравнение Mixer архитектуры с другими SOTA моделями

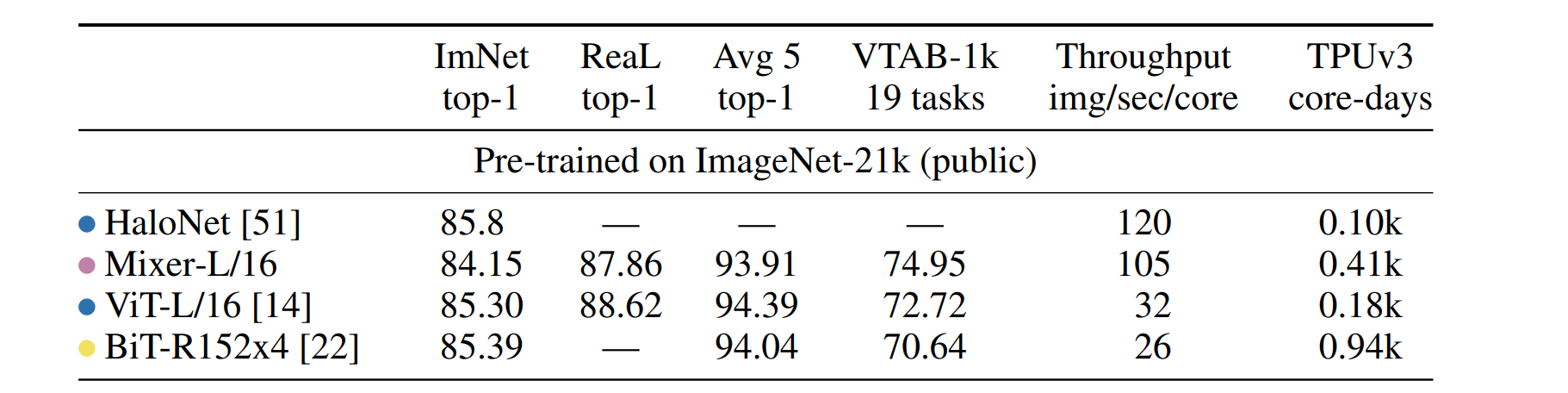
Почему так происходит? Полноценного ответа на этот вопрос нет.

Однако, я совру, если скажу, что никто не пытается это изучать. Выходит множество статей на эту тему: On the Mathematical Understanding of ResNet, The Modern Mathematics of Deep Learning, etc.
Мне нравятся эти статьи, они необходимы и интересны для разработки архитектур под конкретные задачи, однако глобально проблема математического бэкграунда нейронных сетей остается открытой. Сейчас попытки его формализации сфокусированы в основном на работе с отдельными частями сети - слоями, блоками и функциями.
Но, возможно, недостаточно просто смотреть на вопросы сходимости, отдельные блоки сети и т.д.
Возможно, стоит посмотреть на проблему под другим углом?

Графы

Базовый скелет нейронной сети - это граф весов. В таком случае, архитектура сети - ее устройство, всяческие skip-connections, feature pyramids - это различные топологии сети. Топологические, в широком смысле, свойства графа могут задаваться его инвариантами. Таким образом, графы с одинаковыми инвариантами могут пониматься, как одинаковые. Далее мы сфокусируемся на одном конкретном инварианте - полиноме Татта, он будет важен для нас в дальнейшем.

Допустим у нас есть граф G = (V, E) - где V - число вершин, E - число ребер. Тогда полином Татта:

$T_G(x,y)=\sum\nolimits_{A\subseteq E} (x-1)^{k(A)-k(E)}(y-1)^{k(A)+|A|-|V|}$

где k(A) - число компонент связности графа (V, A). Данные полиномы задают широкий спектр различных свойств графа, таких как число деревьев T(2,1), число остовов T(1, 1), etc.
В широком смысле полиномы Татта характеризуют степень связности графа.

Опишем простой пример расчета полинома. Полином Татта может быть рассчитан рекурсивно:

$T_{\emptyset} (x,y) = 1\\ \text{If e is a loop: } T_G (x, y) = yT_{G \backslash e} (x, y) \\ \text{If e is a bridge: } T_{G} = xT_{G/e} (x,y)\\ \text{else: } T_G (x,y) = T_{G \backslash e} (x,y) + T_{G/e} (x, y)$

где G\e - граф G с удаленным ребром e, G/e - граф G, где вершины при ребре e - склеены. Пример:

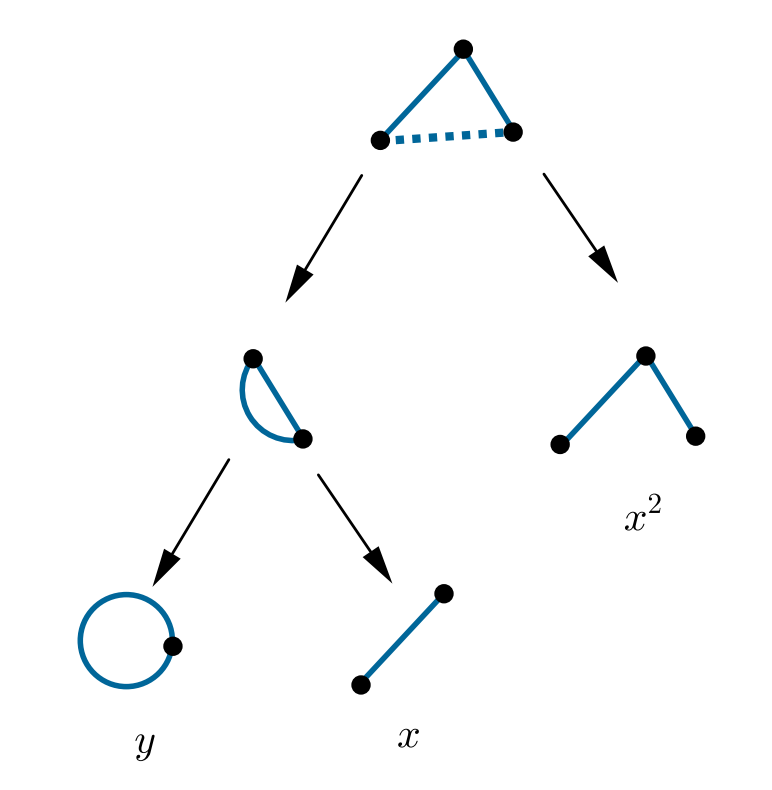
Смотрим на ребро, помеченное пунктирной линией. Полином такого графа распадается на сумму двух:
1) Справа пунктирное ребро удалено
2) Слева пунктирное ребро стянуто. Результат стягивания аналогично распадается на сумму двух других полиномов. В итоге, рекурсивно получаем сумму мономов, указанных на изображении.

Но интересны они нам не только по этому. Простое знание топологии графа не даст нам никакой информации о том, для какого случая какая топология наиболее оптимальна и почему. Нам интересна сходимость нейронной сети, ее поведение, в зависимости от топологии.
Давайте зададимся вопросом: Что такое "хорошая" нейронная сеть? Как формально описать то, что она будет хорошо решать поставленную задачу, в терминах архитектуры? Попытка понять ответ на этот вопрос и приводит нас к следующему разделу...

Эмерджентность

Самое характерное свойство эмерджентной системы: Наличие у системы свойств, не присущих её компонентам по отдельности. Простейший пример эмерджентности, который, я уверен, известен многим из читателей: Клеточные автоматы.

Говоря чуть формальнее: Допустим в вашей среде задан набор простейших агентов с простейшим набором правил. Тогда моделирование их взаимодействия может порождать крайне нетривиальную и сложную динамику.

Но как это все связано с нейронными сетями, графами и полиномами Татта?
На самом деле эмерджентность - это свойство не только клеточных автоматов или их аналогов, но любых сложных систем. То есть систем, состоящих из множества отдельных компонент. И самый характерный пример подобных систем, с точки зрения физики - это фазовый переход.

Простейший пример - модель Поттса на графе:

$H_p = -J_p \sum_{(i,j)}\delta(s_i,s_j)$

где s - векторы, заданные в вершинах графа (будем называть их "спины"), J - коэффициент или матрица смежности графа, H - гамильтониан модели Поттса (энергия), дельта - Кронекера.
Проще говоря, данная модель говорит: чем больше рядом с тобой соседей, таких же как ты, тем тебе лучше (тем меньше твоя энергия).

Поместим такую модель на граф и зададимся распределением, например, Гумбеля:

$F_G (x) = e^{-e^{-x}}$

тогда, считая, что вероятность перехода спина из одного состояния в другое - это вероятность того, что энергия нового состояния будет меньше, чем энергия старого (напомним, гамильтониан - это энергия), получим:

$P(x) = \frac{e^{V(x)}}{\sum_{y \in X} e^{V(y)}}$

где V - энергия соответствующего состояния, X - всевозможные состояния. Температура здесь опущена.

Задавшись такой вероятностью и таким гамильтонианом на графе, мы можем инициализировать все его вершины случайным значением из X и запустить эволюцию данной системы с какого то случайного узла. Результатом станет динамический процесс, который может привести к фазовому переходу.

Но как же все это связано с полиномами Татта, о которых я писал?
Дело в том, что в статистической физике основным математическим инструментом является функция от гамильтониана:

$Z = \operatorname{tr} ( e^{-\beta \hat{H}} )$

Данная функция называется статсуммой и позволяет вычислять различные термодинамические параметры системы.
Если немного покопаться в формулах и разобраться с этой функцией, оказывается, что она, с точностью до множителя, равна полиному Татта. Таким образом, между теорией фазовых переходов и теорией графов есть прямая связь.

Теперь мы можем вычислять термодинамические параметры модели в зависимости от топологии графа.

Но к чему весь этот пассаж о фазовых переходах?
Дело в том, что нейронные сети, по своей сути, являются сложной системой. Но, что более интересно: в них есть фазовые переходы. И тут можно задаться вопросом: А вдруг возможно этот же фреймворк использовать для анализа зависимости свойств нейронной сети от ее архитектуры?
И это так. Вспомним вопрос: Как мы можем понять, что такое "хорошая архитектура"?

Формальный ответ: Та нейронная сеть, которая находит глобальный минимум нашей функции потерь для заданного датасета.

Неформальный ответ, который можно дать после вышеописанного обзора: "Хорошая" нейронная сеть - это та, для которой существует фазовый переход для данной задачи.

Послесловие

На самом деле я не упомянул еще важную взаимосвязь: Известно, что нейронные сети, по крайней мере в каких то случаях, могут быть переформулированы в теоретико-игровых терминах как задача поиска решения для какой то игры. И на самом деле, в каком то смысле, некоторые равновесные состояния в теории игр соответствуют фазовым переходам из статистической физики (модель Поттса <=> QRE).

Таким образом, у нас есть дорожка, идя по которой можно попытаться построить фреймворк для анализа процесса обучения нейронных сетей, с точки зрения равновесия на графе, в зависимости от топологии этого графа.

Такой подход позволил бы нам учитывать коллективное поведение нейронной сети в целом, а не свойств отдельных ее элементов.

Комментарии (30)

MasterMentor
30.07.2023 15:12
#25804528
Больше всего в статье понравилось это:

Сразу предупреждаю - я не являюсь каким то глубоким специалистом в этих сферах.
1. DeadPhilosopher Автор
  30.07.2023 15:12
  #25804792
  +3
  Дисклеймер, который должен сподвигнуть более шарящих людей поправить меня в местах, где я мог ошибиться =)

anonymous
30.07.2023 15:12
#25804530
НЛО прилетело и опубликовало эту надпись здесь
1. DeadPhilosopher Автор
  30.07.2023 15:12
  #25804534
  Ну, в некоторых областях нейронок действительно "революция на каждый день". В особенности хорошо это было видно в 21 году, где то недалеко от нового года, когда друг за другом несколько версий Yolo вышло и SWIN, и все аутперформили остальные конкурентов.
  Но я ничего не пытаюсь строить. По описанному тут и так есть статьи =)
  1. anonymous
    30.07.2023 15:12
    #25804624
    НЛО прилетело и опубликовало эту надпись здесь
    
    DeadPhilosopher Автор
    30.07.2023 15:12
    #25804788
    Все указанное тут - есть в статьях. Ссылки на них даны. Просто прям в какую то цельную кучку оно обычно не собрано. Обычно это статьи вроде "а сейчас мы опишем нейронки теорией игр", "а сейчас мы найдем в нейронках фазовые переходы", а вот между собой это обычно не связывается. И т.д.
    Ну и вообще, наезда не понял =)
    
    anonymous
    30.07.2023 15:12
    #25804844
    НЛО прилетело и опубликовало эту надпись здесь
    
    DeadPhilosopher Автор
    30.07.2023 15:12
    #25804852
    Если вы хотите статью про yolo - вы читаете статью про yolo, если вы хотите статью про трансформеры - вы читаете статью про трансформеры =)
    А вообще, по "горячим" источникам - лучше читать, собственно, источники.
    
    Но наверное структуру надо будет поправить.
    
    anonymous
    30.07.2023 15:12
    #25804858
    НЛО прилетело и опубликовало эту надпись здесь
    
    DeadPhilosopher Автор
    30.07.2023 15:12
    #25804870
    Узнать об альтернативных методах изучения нейронных сетей.
    
    anonymous
    30.07.2023 15:12
    #25804898
    НЛО прилетело и опубликовало эту надпись здесь
    
    funca
    30.07.2023 15:12
    #25805022
    +1
    А чего я должна хотеть, чтобы читать вашу статью?
    
    В самом деле, расскажите чем привлекла вас эта статья, чтобы зарегистрироваться на сайте и писать к ней комментарии?

VPryadchenko
30.07.2023 15:12
#25805210
Хорошая статья, жаль, только, на самом интересном месте закончилась:)
1. DeadPhilosopher Автор
  30.07.2023 15:12
  #25805254
  +1
  К сожалению, прям огромного числа статей про зависимости сходимости от топологии - я не наблюдал :( Недоисследованная область, имхо.
  1. S_A
    30.07.2023 15:12
    #25805756
    
    Сходимость зависит не только от архитектуры, но и от процедуры.
    
    Кстати, уверен вам будет интересно ознакомиться с концепцией ограниченной машины Больцмана
    
    DeadPhilosopher Автор
    30.07.2023 15:12
    #25806626
    
    Конечно. Но у архитектуры роль, в каком то смысле, больше. Это хорошо видно на примере трансформеров - после их появления сети на такой архитектуре начали аутперформить конкурентов не только в своей области NLP, но и в CV и других областях. И в принципе, вполне реально анализировать вклад именно архитектурной составляющей, фиксируя процедуру.
    
    Да, почитаю, спасибо =)
    
    S_A
    30.07.2023 15:12
    #25811510
    +2
    У архитектуры конечно же роль больше - потому что процедуры by design решают одну и ту же задачу, а архитектуры - разные. У Microsoft даже была архитектура neural architecture search. Перформила вполне до трансформеров.
    
    В принципе трансформеры перформят потому attention - он человекоподобен (размечает кто?..). На физических задачах скажем, есть свои ноу-хау, как и в тех же экономических.
    
    Ваша находка так или иначе впечатлила - кодирование архитектуры с некоторыми свойствами. Нет уверенности, однако, что только архитектура достаточна для перфоманса, я об этом.
    
    В продолжение (топологической) мысли - процедуру было бы идеально переложить в теорию узлов и зацеплений, которая различает только количество путей из одной точки в другую. То есть оптимизатор мог бы разветвляться на разные траектории. Это не то чтобы из разряда фантазий, скорее некоторая намётка.
    
    Вкратце: рельеф лосс-функции - результат архитектуры, но ввиду наших слабых вычислительных возможностей, имело бы смысл иметь топологические инварианты именно рельефа функции потерь, и идеально если бы они содержательно вязались бы с инвариантами архитектур

berng
30.07.2023 15:12
#25805740
С вниманием все может объясняться с такой точки зрения: самая простая интерпретация внимания - это оптимальная перестановка значений входной величины (немонотонное преобразование), и поэтому если за вниманием стоит простая модель, типа регрессии (или полносвязного слоя, например), регрессия будет работать эффективнее, чем без внимания. Если за вниманием стоит модель более сложная, чем регрессия - возможно внимание и не даст такого сильного эффекта, как в случае с регрессией, но эффект все-равно по идее должен быть не хуже (предполагаем, что мы можем обучить корректно это внимание, а здесь дополнительные свободные параметры требуют дополнительного объема датасета и более аккуратной тренировки. И конечно помним, что "не хуже" не означает "лучше", и поэтому нет гарантии, что увеличение параметров/добавление внимания даст эффект) - для любой последующей сети должна существовать оптимальная перестановка входных значений, при которой модель работает наилучшим образом, хотя возможно внимание в каких-то слоях работает впустую. Поэтому мне внимание нравится - его использование иногда позволяет мне использовать более простые сети после него, хотя с очень сложными сетями я его не использовал.

И статья интересная, спасибо - сети сейчас действительно бурно растут в смысле не только результатов, но и размера. И уже не всегда понятно - стоит предлагаемое увеличение размеров сети полученных результатов, или нет: может 99% элементов сети работает вхолостую. Мне приходилось сталкиваться со случаями, когда сильное увеличение размера сети не приводило к улучшению результатов, а иногда и ухудшало их.
1. DeadPhilosopher Автор
  30.07.2023 15:12
  #25806604
  +2
  может 99% элементов сети работает вхолостую
  
  Не может, на самом деле так и есть =) Дистилляция моделей и lottery ticket hypothesis это прекрасно демонстрируют. Подавляющая часть работы решается очень маленькой подсетью огромной сети. Собственно, сейчас вроде почти любые модели стараются дистиллировать, ибо иначе они слишком огромные и требовательные.
  
  Ко вниманию как таковому претензий нет - тут суть в том, что в трансформерах основной профит приходится не с механизма внимания, а с чего то другого.
  1. VPryadchenko
    30.07.2023 15:12
    #25806644
    +1
    Не успел написать коммент, но добавлю, что правильно приготовленный прунинг тоже) На практике доводилось срезать до 70 % весов бинарного классификатора без потери точности и даже немного улучшая обобщающую способность.
  1. VPryadchenko
    30.07.2023 15:12
    #25806670
    +1
    Если посмотреть на граф трансформера (по крайней мере ViT, работал только с ними), станет очевидно, что трансформер - это буквально разложение функции в ряд: f(x) = x + A(x) + B(x + A(x)) + C(x + A(x) + B(x + A(x))) + ... = x + A'(x) + B'(x) + C'(x) + ...
    Механизм внимания просто определяет вид операторов. То же самое делается, например, в MLP миксерах - просто вид оператора другой. Не берусь утверждать на 100%, но, полагаю, любые трюки для оптимизации модели путём изменения механизма внимания - это все пляски вокруг поиска более оптимального вида A, B, C...
  1. berng
    30.07.2023 15:12
    #25806786
    Насколько я понимаю, в трансформере профит идет за счет многоголовости внимания. По факту на каждом многоголовом внимании вы тренируете не одну сеть, а их ансамбль, где каждой сети соответствует своя голова внимания. Этот ансамбль дальше разгребается (уточняется, комбинируется) следующим слоем, то есть фактически многоголовое внимание - это стекинг из простых одноголовых сетей, за счет стекинга и профит. Хотя я могу ошибаться.
1. Alexey2005
  30.07.2023 15:12
  #25807802
  +3
  Суть внимания в нейронках проста как мычание: это всего лишь способ ввести в нейронную сеть операцию умножения.
  Если посмотреть, как "работает" классический искусственный нейрон, то можно увидеть, что он полностью построен на сложении: он просто складывает все пришедшие на него взвешенные сигналы со всех входов, и выдаёт эту сумму на выход в преобразованном виде. То есть нейрон — это такой нелинейный сумматор.
  Но вот теперь мы хотим выделить в нашем потоке данных какие-то интересные области, отбросив всё ненужное. Как это сделать? Самый простой способ — пресловутая "маска", альфа-канал. Когда каждый элемент (например, пиксель входного изображения) домножается на некоторое число альфа-канала. Важные области так можно усилить, менее важные — ослабить, а лишнее вообще домножить на ноль, чтобы более глубокие слои сети на них не отвлекались.
  Но как это сделать, если нейроны не умножают, а только складывают? Нет, конечно глубокая сеть может эмулировать операцию умножения, но для этого она сперва должна "догадаться" это сделать.
  Поэтому операцию перемножения входных каналов вводят в явном виде. В структуру вводится такой блок, который не складывает все свои входные значения, а перемножает их и выдаёт дальше произведение.
  При этом мы получаем такой настраиваемый фильтр-маску, который и выделяет правильные области. Естественно, что таких масок может быть несколько.
  Этот блок и называют блоком внимания. Всё остальное, все эти key-query-value и прочие "механизмы внимания" — это просто способ уменьшить ресурсоёмкость подобных блоков. Дело в том, что умножение, в отличие от сложения, куда более ресурсоёмко. А ведь при обучении этого куска сети ещё и дифференцировать требуется. Взять производную от суммы куда как проще, чем от произведения. Поэтому "внимание" вычислительно затратно. Крайне затратно. И памяти жрёт тоже намного больше, отсюда и все эти пляски с бубном по поиску разных хитрых алгоритмов внимания.
  1. berng
    30.07.2023 15:12
    #25808496
    +1
    Насчет умножения - это зависит от того, какой тип внимания вы используете, там их много разных вариантов (https://arxiv.org/abs/1508.04025v5). Если вы посмотрите, на (https://arxiv.org/pdf/1706.03762.pdf , eq.1), то там видно, что максимум софтмакса достигается тогда, когда Q является перестановкой K. По-моему, умножения как такового там нет, просто очень хитрый подбор оптимальной перестановки координат вектора V. Хотя я могу ошибаться. Но в той-же location-based attention (https://arxiv.org/abs/1508.04025v5, eq.8) вообще этот перестановочный характер внимания очевиден: никакого умножения там нет, просто подбор матрицы оптимальной перестановки координат.
    
    А главное, по теории (универсальная теорема аппроксимации, теорема Колмогорова-Арнольда и т.д.) умножение входов не может являться базовой бинарной операцией, позволяющей проводить универсальную аппроксимацию, там в УТА допустимо в качестве бинарной операции только сложение, и это доказано. Поэтому нейроны и свертки в нейронных сетях можно, а умножения каналов - нельзя, иначе аппроксимация не сойдется. Я конечно могу ошибаться, но вижу это так.

Yermack
30.07.2023 15:12
#25807188
+1
Кстати, поиски "фазовых переходов" стали модны не только для искусственных нейронных сетей, но и для настоящих: https://www.youtube.com/watch?v=vwLb3XlPCB4
В этом же видео есть ссылка на бомбезную книгу по этой теме.

azTotMD
30.07.2023 15:12
#25807190
Спасибо, очень интересная статья.

Особенно поразило вот это "добавлении блока без входа". Понимаю, что это больше вопрос к авторам той статьи (обязательно посмотрю её подробнее), а не к вам, но "блок без входа" - это ведь константа? Но зачем-то авторы изобразили этот блок в виде нейросети? С таким же успехом, это мог быть биас? Любопытно, что в классификаторах, типа реснета, последний классифицирующий слой содержит биасы. Получается, что если два первых класса набрали одинаковые значения логитсов выигрывает тот, у которого биас больше. Как если бы нейронка сказала: "да вот эти два класса набрали одинаково, но вот класс1 встречается чаще - поэтому пусть это будет класс1". Некое такое априорное знание
1. DeadPhilosopher Автор
  30.07.2023 15:12
  #25807272
  +1
  Блок без входа = тензор (или нейронная сеть) - которые содержат обучаемые параметры. Т.е. обратное распространение ошибки через них проходит, но нет входа.
  1. azTotMD
    30.07.2023 15:12
    #25807362
    Но в ходе инференса, то ведь это - константа? Ну т.е. по сути - это просто хитрый биас?
    
    DeadPhilosopher Автор
    30.07.2023 15:12
    #25807374
    +1
    Типо того, да. Ну правда, байес все таки аддитивный, а эта штука может играть роль маски, умножаться разными способами, конкатенироваться, складываться и т.д.

onuphrienko
30.07.2023 15:12
#25808176
Интересная статья, с удовольствием буду ждать новых!

Нейронные сети, графы и эмерджентность +27

Нейронные сети

Графы

Эмерджентность

Послесловие

Комментарии (30)

DeadPhilosopher Автор

DeadPhilosopher Автор

DeadPhilosopher Автор

DeadPhilosopher Автор

DeadPhilosopher Автор

DeadPhilosopher Автор

DeadPhilosopher Автор

DeadPhilosopher Автор

DeadPhilosopher Автор

DeadPhilosopher Автор