Вообще, до сих пор неясно, кто изобрёл первый цифровой компьютер. Кандидатов много, и все они относятся к 30-м и 40-м годам ХХ века. Например:

• в 1938 году Конрад Цузе создал Z1 — первую машину, которая помогала в аэродинамических расчётах;

• в 1940 году Алан Тьюринг создал компьютер, способный расшифровывать код «Энигмы»; 

• в 1942 Атанасов и Берри разработали компьютер, названный в их честь. В 1973 году Федеральный суд США даже официально постановил, что эта машина — первый компьютер, но у многих остались сомнения;   

• в1946 году Джон Мокли разработал ЭНИАК — вычислительное устройство для расчёта баллистических таблиц.  

Но примечательно, что на звание первого компьютера претендует и компьютер Mark I, созданный в 1944 году. При этом руководитель группы разработчиков Говард Эйкен при создании машины ориентировался на наработки Чарльза Бэббиджа — английского математика начала 19 века, который пытался создать разностную машину для решения полиномиальных уравнений. К сожалению, у Бэббиджа ничего не вышло, но его идеи однозначно опередили своё время. Посмотрим на его жизнь и изобретения.

С чего всё началось

Жарким летом 1821 году в тесном кабинете Королевского астрономического общества в Лондоне над столом склонились двое молодых людей — обоим тогда было 28 лет. Они кропотливо просматривали астрономические таблицы «Морского справочника» 1776 года выпуска, перелистывая страницу за страницей и поражаясь, сколько в таблицах допущено ошибок. А это плохо не только для астрономов, но и для морской навигации. 

Один из молодых людей — некий Джон Гершель,— не выдержав очередной ошибки, воскликнул: «Вот бы можно было исключить людей из процесса расчёта! Ведь тут простейшие ошибки в сложении и вычитании — это же можно как-то механизировать. Тем же паром, а?». В этот момент его коллега Чарльз Бэббидж замер и произнёс историческое: «Вполне возможно».

«Необнаруженная ошибка в логарифмической таблице подобна затонувшей скале в море», — говорил Джон Гершель 

С этого момента Бэббидж приступил к разработке, уникальной для того времени, разностной машины. В то время господствовала идея барона де Прони — огромные тригонометрические или логарифмические таблицы составлялись вручную, но при этом использовался принцип разделения труда на три уровня:

• первый уровень, самый верхний — несколько выдающихся математиков описывают функции и уравнения, по которым будут составляться таблицы;

• второй уровень, промежуточный — не менее выдающиеся технологи находят способ, как оптимально выстроить рутинный процесс вычислений;

• третий уровень, самый примитивный — вычислители считают и кропотливо записывают в таблицы соответствие функций разным аргументам с определенным шагом. 

Именно на третьем уровне и происходили все ошибки. Причём обычно исполнителям вообще не надо было разбираться в математике, а только уметь складывать и вычитать — это позволяло экономить на квалификации счетоводов. Бэббидж понял, что этот третий уровень, и может заменить машина, сократив число ошибок и ускорив процесс расчётов. 

В то время как раз шла промышленная революция, которую ещё называли «паровой» — машины Уатта и Ползунова внедрялись везде, где только можно. Почему бы не использовать пар и в качестве привода такого вычислительного устройства? Правда, забегая вперёд, нужно отметить, что дальше разговоров дело не пошло — машины Бэббиджа управлялись всё-таки вручную. 

Конечно, Бэббидж знал об опыте своих предшественников — попытки облегчить труд счетоводов предпринимались уже неоднократно. 

Например, примечательна работа Джона Непера — создателя логарифмов и человека, который первым понял, что более сложные операции умножения, деления или извлечения корня можно заменить на простое сложение и вычитание. Непер разработал так называемые «палочки Непера» — простой калькулятор 17 века, помогавший перемножать числа.

Через несколько лет Уильям Отред придумал первую логарифмическую линейку, а в 1642 году Паскаль изобрёл первый механический калькулятор — Pascaline. Машина управлялась ручным вращением дисков и могла складывать и вычитать два числа, а также выполнять умножение и деление путём многократного сложения или вычитания.

Но задача у Бэббиджа стояла более общая. Дело в том, что при расчётах астрономических таблиц использовались функции не только первого порядка. Как известно, практически любую функциональную зависимость (а это и есть таблица) можно описать в виде полинома n-го порядка с разными степенями аргумента и коэффициентами при нём. Например, уравнение y=5x4+2x3+6x2+10x+55 — полином 4-го порядка. 

Нужно было найти, как можно быстро и просто механически вычислять значение Y при разных целочисленных X. Для этого Бэббидж использовал метод разностей: он заключается в некотором свойстве полиномиальных уравнений. 

Например, есть простая функция y= x3, третьей степени. Для неё можно составить таблицу, в которую мы подставим несколько маленьких Х (скажем, от 1 до 3) и легко посчитаем значение Y. При этом рядом нарисуем ещё один столбец, в котором будем вычислять разницу соседних значений — 1D. Получится:

• для X=0 значение Y=0

• для X=1 значение Y=1 — разница между этим значение и предыдущим будет (1-0)=1

• для X=2 значение Y=8 — разница между этим значение и предыдущим будет (8-1)=7

• для X=3 значение Y=27 — разница между этим значение и предыдущим будет (27-8)=19

А теперь давайте вычислим разницу 2-го порядка и 3-го порядка между разностями, найденными нами сейчас. 

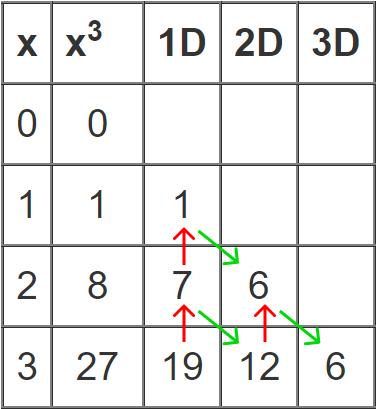
Полученная разность 3-го порядка для многочлена 3-й степени дальше будет постоянной — это и есть основное свойство. Проверим:

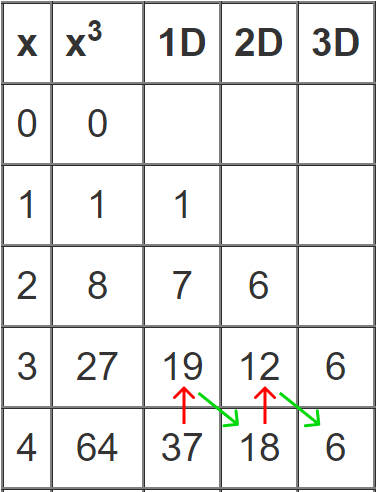
Всё сходится: для вычисления значения X=5 нам надо только: 

• знать предыдущие разности от Х=4

• знать разницу третьего порядка — в нашем случае 6. 

Давайте построим таблицу, проведя обратную операцию: последовательно будем складывать разницы в обратном порядке. Получим:

1. 6 + 18 = 24 (третий порядок)

2. 24 + 37  = 61 (второй порядок)

3. 61 + 64 = 125 (первый порядок — это и есть искомое число)

Это же работает с многочленами любой степени и сложности. Нам надо только знать значение n-й разности (константы), а также значение разностей на предыдущем шаге, которые мы можем посчитать без ошибок. 

Остаётся построить механизм, который будет итерационно складывать числа до того значения, какое вам надо. Мы выставляем положения циферблатов на начальной позиции (известные нам разности), а дальше просто вращаем ручку столько раз, сколько должно быть последовательных сложений — всю работу делают шестерни. Мы ограничены только в размерах установки: 

• чем большие числа мы хотим складывать, тем выше должны быть наборы циферблатов — иначе нам не хватит разрядов;

• чем больше степень многочлена, тем больше таких столбцов с числами должно быть.

Ещё Бэббидж решил, что надо исключить любую ошибку. Поэтому важной частью его концепции стала система печати — значения вычислений выдавливались на медной пластине. 

В общем, концепция разностной машины была готова в том же 1821 году, а на её проектирование и презентацию научному сообществу ушёл ещё год. Но вернёмся к этому позже. 

Ранние годы

Бэббидж был невероятно талантливым человеком для своего времени: его интересы не ограничивались одной только математикой. И во многом на судьбу гения повлияло его хрупкое здоровье. 

Родился Чарльз Бэббидж в 1791 году в семье банкира, в довольном фешенебельном районе Южного Лондона — Ньюингтоне. В нежном восьмилетнем возрасте малыш подхватил лихорадку, которая чуть не унесла его жизнь. Поэтому его отправили в приходскую школу, где он обучался у частных репетиторов — чтобы окончательно не подорвать здоровье. Он так и не пошёл в общеобразовательную школу, зато во время домашнего обучения познакомился с его любимой книгой Ward's Guide for Young Mathematicians. 

В 1810 году Чарльз Бэббидж, 18 лет отроду, поступает в самый престижный в Англии Тринити-колледж, при Кембриджском университете. На секундочку, из этого колледжа в разное время выпускалось шесть премьер-министров, а также Исаак Ньютон, Джеймс Клерк Максвелл, Эрнест Резерфорд и Нильс Бор.  

Каково же было разочарование Бэббиджа, когда он познакомился с процессом обучения в столь «передовом» учебном заведении. Что уровень преподавания, что учебная программа никуда не годились. Причём он не один это понимал — Джон Гершель и Джон Пикок, ещё один талантливый математик, полностью разделяли взгляды Бэббиджа. 

Так, в в 1812 году родилось «Аналитическое общество», и оно поставило себе задачу ликвидировать разрыв в математическом подходе между Англией и континентальной Европой. Например, Бэббидж со товарищи хотели, чтобы английские математики перешли на нотацию Лейбница при работе с дифференциальными уравнениями вместо устаревшего подхода Исаака Ньютона. Для этого они даже перевели на английский знаменитый учебник «Научные основы интегрального и дифференциального исчисления» французского математика Сильвестра Лакруа. 

В том же 1812 году Бэббидж переводится в другой колледж при Кембридже — Питерхаус (во многом, из-за неприязни преподавателей), и в 1814 году успешно его заканчивает, являясь неофициальной звездой математики среди всего потока студентов. 

После выпуска он около года читал лекции в Королевском институте, а в 1816 году за заслуги был избран членом престижнейшего Королевского общества. 

Создание разностной машины

В 1820 году Бэббидж и Гершель, активно интересовавшиеся астрономией, создают Астрономическое общество Лондона (к слову, в 1831 году оно получило звание «Королевского» с соответствующими привилегиями). Именно здесь мы возвращаемся к точке, когда было принято решение о создании разностной машины. 

14 июня 1822 году на свет появляется одностраничная заметка «О применении машин для расчёта астрономических таблиц» — вот она. 

Если кратко, то автор утверждает, что он построил механизм, который успешно рассчитывает таблицы «квадратных и треугольных чисел», а также полином второго порядка x2 + x+ 41. Он заканчивает свою записку с большим оптимизмом: 

«Исходя из опытов, которые я уже провёл, я чувствую большую уверенность в полном успехе предложенных мною планов».

Первая версия разностной машины, конечно, была экспериментальной — работала только с числами до шестого разряда и полиномами второго порядка. А у Бэббиджа были намного более грандиозные планы — построить машину, которая бы работала с числами до 20 знаков и многочленами шестого порядка, причём не только в десятичной системе счисления. По проекту новая версия разностной машины должна была содержать 25 000 деталей и весить около 4 тонн — при этом она могла бы делать оттиски на носителях с результатами расчётов, что является прообразом современного принтера. 

В 1824 году Бэббидж получил почётную медаль «Астрономического общества» за работающий прототип разностной машины, и в том же году получил средства в размере 1700 фунтов стерлингов (около 230 000 долларов США сейчас) для начала работы над проектом. Правительство увидело мощнейший потенциал в разностной машине, причём не только для астрономов: например, для инженерных и баллистических расчётов, в банковских и страховых таблицах, и многого другого.

На тот момент задача была практически неподъёмной: в 19 веке изготовить настолько точно шестерни и валы с учётом допустимого люфта было крайне сложно. А точность была очень важна: в разностном методе суммирование происходит последовательно, в несколько этапов. Если хоть один диск не сместится на нужную величину, то все последующие стадии расчётов будут содержать ошибку. 

Для такой работы нужен был опытный мастер, и Бэббидж обратился к Джозефу Клементу — изготовителю сверхточных инструментов и ткацких станков. О подходе Клемента к работе говорит интересный факт: он производил резьбовые метчики и настаивал, что должен быть разработан общий стандарт резьбы. Его подмастерье Джозеф Уитворт использовал эти идеи и создал первый в мире стандарт BSW — British Standard Whitworth.

Дальше между Бэббиджем и Клементом установились довольно странные отношения. В течение почти 9 лет они плотно сотрудничали и создавали невероятно точные детали, которые невозможно было нигде купить. Но при этом они часто спорили: Бэббидж вносил непрерывные изменения в конструкцию и стремился к идеальному результату. А Клемент настаивал, что нужно придерживаться бюджета — каждая новая деталь стоила очень дорого. 

В 1832 седьмая часть всей машины, состоящая примерно из 3000 деталей, была готова. При этом бюджет вырос с 1700 до 17 000 фунтов, и Бэббидж выложил ещё около 6 000 фунтов из своего кармана. Для финансирования работающий образец регулярно демонстрировали публике. Одна из зрительниц вспоминала: 

В прошлый понедельник мы пошли смотреть на мыслящую — или как-то так она называлась. На наших глазах она возвела несколько чисел во 2-ю и 3-ю степени, а потом нашла корень квадратного уравнения».

Но в целом работа двигалась катастрофически медленно. Развязка наступила в 1833 году — разработка разностной машины переносится в новую просторную мастерскую. На время переезда рабочие не работали, и Клемент просит Бэббиджа компенсировать им простой в работе. Тот отказывается, и Клемент прекращает сотрудничество: забирает инструменты и распускает рабочих. На этом история создания разностной машины версии 1.0 заканчивается. 

Только в 1847 году Бэббидж вернулся к идее довести до ума разностную машину, создав её версию 2.0 — она могла бы уже работать с числами 31 порядка и полиномами седьмого порядка, при этом иметь всего 8000 деталей благодаря новому подходу. Однако финансировать очередной проект правительство не собиралось — тем более никто не отчитался за израсходованные 17 000 фунтов на постройку предыдущей версии устройства. Да и тогдашний премьер-министр Роберт Пил терпеть не мог взбалмошного изобретателя.

Шведский изобретатель Георг Шутц построил машину на основе идеи Бэббиджа в 1855 году. Но она была намного скромнее: работала с числами 15-значными числами и полиномами четвёртого порядка. Кстати, сам Бэббидж всячески поддерживал Шутца и популяризовал его машину. 

Но кажется, что на самом деле Бэббидж несильно расстроился из-за провала своей разностной машины. С 1833 года вплоть до своей смерти он грезил другим, более совершенным устройством. 

От разностной машины к компьютеру

Бэббиджу пришла в голову идея, что можно сделать машину общего назначения, которая сможет решать больше разных задач. Например:

• Производить не только операцию сложения, но и любые другие, которые оператор будет выбирать по желанию: квадратный корень, умножение, деление и прочее. Тем более все они так или иначе выполняется путем сложения и вычитания.  

• Данные будут не просто вводиться оператором, а ещё и сохраняться в некое хранилище — например, промежуточные результаты вычислений. 

• Чтобы машина понимала, какую операцию сделать и при каких условиях поместить результат в регистр хранения, можно использовать перфокарты с натурально написанными программами. Надо признать, что тут Бэббидж использовал идеи Жозефа Жаккарда, который еще в 1801 году придумал перфокарты для автоматизации плетения сложных ткацких станков. 

Если очень упрощённо, машина состояла из базовых элементов, которые можно встретить в любом современном компьютере: 

• Store (хранилище) — тут будут храниться данные с результатами вычислений. Память в современной терминологии — представляет собой шестерни с циферблатами, расположенные столбиками. Чем большее значение числа должно быть записано, тем больше будет высота столба.

• Mill (мельница) — то, что будет производить непосредственные арифметические операции и передавать данные либо на печать, либо в промежуточное хранилище. Выполняет функцию процессора — соединяет шестерни в разных комбинациях, в зависимости от исполняемой программы.

• Устройства ввода и вывода — это принтер (примерно тот же, что планировалось использовать в разностной машине), звонок (сообщение о том, что программа исполнилась) и набор разных перфокарт, которые позволяли пользователю буквально программировать машину!

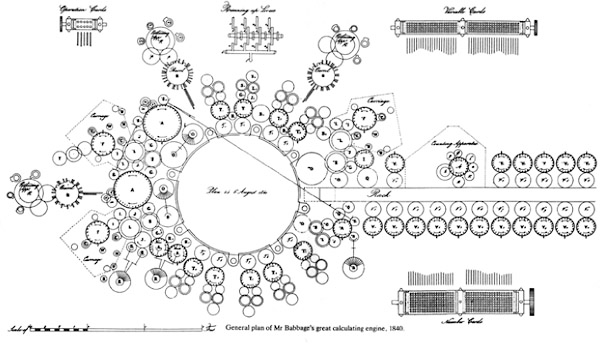
Сами перфокарты использовались трёх видов:

• операций — указывали, что сейчас должно исполняться: умножение, сложение, вычитание или деление;

• переменных — сообщали, что должно происходить с результатами вычислений или откуда брать входящие данные: из хранилища или от пользователя;

• числового ввода — с их помощью пользователь вводил конкретные цифры, и на этих же перфокартах данные могли сохраняться, как на дискетах. 

Комбинируя перфокарты и расставляя на них отверстия в нужном порядке, можно было составлять ветвления и циклы — неотъемлемую часть современной разработки. Поэтому можно сказать, что все признаки программируемого компьютера у аналитической машины Бэббиджа были на лицо. На выполнение операций сложения/вычитания уходило бы примерно 1 секунда, а на умножение и деление — 40-50 секунд.

Подробное устройство аналитической машины Чарльза Бэббиджа описывается в книге «Невероятные приключения Лавлейс и Бэббиджа. (Почти) правдивая история первого компьютера».  А ещё есть замечательная статья на Хабре по мотивам книги с оригинальными иллюстрациями — рекомендуем к прочтению. 

В 1840 году Чарльз Бэббидж прочитал в Италии несколько лекций о своей аналитической машине. Это настолько шокировало слушателей, что итальянский математик Луиджи Федерико Менабреа написал в 1842 году статью «Понятия об аналитической машине». 

Опубликованную статью заметила Ада Лавлейс — урождённая Ада Байрон, единственная дочь великого английского поэта лорда Байрона. 

Надо сказать, что статья попалась Аде на глаза не случайно. Ещё будучи подростком, она увидела в действии разностную машину Бэббиджа и настолько заинтересовалась ей, что принялась постигать математику — хотелось разобраться в принципе её действия. Они даже подружились с изобретателем, и Чарльз помогал своей подопечной в учёбе — он отмечал, насколько у Ады развиты аналитические способности.

Поэтому Ада внимательно следила за работами Бэббиджа и не могла не заметить статью итальянского математика. Но она нашла в ней... Ошибки! Когда она поделилась с Бэббиджем своими замечаниям, тот восхитился и предложил ей написать комментарии. Ада написала — её «Заметки» 1843 года с переводом статьи по объему были в три раза больше оригинала. Примечательно, что в них она предложила довольно сложную методику расчёта чисел Бернулли. Вот текст самих заметок, а подробно методику разбирают в статье на Хабре. 

Бэббидж создал десятки чертежей своей аналитической машины, а также описания некоторых алгоритмов. Однако аналитической машине не суждено было быть построенной при жизни изобретателя во многом из-за того же, почему так и не была построена более примитивная разностная машина. Всему виной отсутствие финансирования и нужных технологий в 19 веке. 

«Я дошёл до момента, когда моих финансовых возможностей и моральных сил не хватает. Поэтому на этом вынужден отказаться от работы над аналитической машиной», — писал в 1851 году Бэббидж в своём дневнике. 

После смерти Чарльза Бэббиджа в 1871 году попытки создать аналитическую машину предпринимал его сын Генри. С 1880 по 1910 он создал несколько небольших узлов, без возможности программирования или хранения данных. Никаких значимых результатов он добиться не смог. 

Судьба разработок Бэббиджа

7 августа 1944 году в Гарвардском университете был официально запущен компьютер Mark I, разработанный на деньги Военно-морского флота США и компании IBM.

Это было настоящим чудом техники. Корпус из нержавеющей стали содержал почти 800 тысяч деталей вроде реле, тумблеров и прочего, имея длину под 20 метров, высоту 3 метра и вес 4,5 тонны. Длина проводов для коммутации составляла около 800 км, а для синхронизации модулей расчёта использовался вал длиной 15 метров, который вращался благодаря электродвигателю больше 4 кВт. Компьютер мог совершать математические операции с 72 числами по 23 разряда каждый, а выполнялись расчёты при помощи считывания данных с бумажной перфорированной ленты. 

Ничего не напоминает? Руководил проектом Говард Эйкен — капитан ВМФ США. И за основу он взял наработки и чертежи Чарльза Бэббиджа! 

Кстати, в основе создания компьютера Mark I лежит так называемая гарвардская архитектура ЭВМ — ровно тот же подход использовал Бэббидж при разработке своей аналитической машины.

«Боюсь, если бы Бэббидж родился на 75 лет позже, я остался бы без работы», — говорил Говард Эйкен

Компьютер Mark I проработал до 1959 года и использовался в основном для составления таблиц функций Бесселя. Особого практического применения он так и не нашёл. 

Но на этом история изобретения Бэббиджа не закончилась. В 1985 году, спустя более чем 100 лет с момента смерти изобретателя, Лондонский Музей науки решил всё-таки реализовать последнюю версию разностной (не аналитической) машины Бэббиджа. На это у них ушло 17 лет — это при современных-то технологиях! Поэтому шансов, что машину могли бы построить в 19 веке при жизни участников процесса, было немного. Вот как выглядит машина в работе. 

Остаётся только гадать, как выглядел бы мир, если бы Бэббиджу всё-таки удалось создать компьютер ещё в 19 веке. Причём его интересы не ограничивались только вычислительными машинами или составлением математических таблиц:

• Написал в 1832 году книгу об организации производственного процесса и важности разделения физического и умственного труда

• Написал в 1837 году теологический трактат, в котором рассуждал о роли Бога и трактовании Библии. 

• Взломал в 1854 году шифр Виженера во время Крымской войны, первым в истории.

• Опубликовал в 1825 году работу в области электродинамики, пытаясь описать причины вращения Араго — основополагающая работа Фарадея по электромагнитной индукции была опубликована только спустя 6 лет. 

Так что Чарльз Бэббидж по праву считается одним из людей, которые своими работами повлияли на историю человечества.