В предыдущей статье, мы разбили все имеющиеся отрезки по точкам пересечений, гарантируя таким образом, что у нас больше нет пересекающихся отрезков. В этой части мы будем стыковать полученные отрезки в контуры и определять их заливку.

Поиск контуров

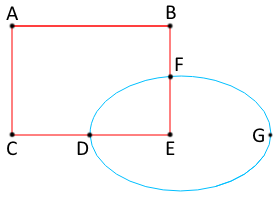Итак, у нас есть набор непересекающихся отрезков. Давайте поищем контуры, которые нам пригодятся для выявления полигонов. На рисунке справа мы видим 6 красных отрезков и 3 синих. Хорошо бы найти контуры ABFDC, DFE и FGD. Составные контуры (например, ABFGDC) нас не интересуют, а значит либо наш алгоритм не должен на них натыкаться в принципе, либо же нам придётся исключать эти контуры позднее.

Поиск перебором

Первый пришедший мне на ум алгоритм изначально неплохо себя показал. Вот как он выглядит:

1. Для простоты, удваиваем количество отрезков, добавляя для каждого отрезка его обратно направленного клона (это позволит нам ходить по отрезкам как по векторам, без необходимости ходить по отрезкам «назад»).
2. Последовательно берём каждый отрезок за начальный для искомого контура, помещаем его в новый массив и вызываем рекурсивную процедуру поиска (ниже).
3. Перебираем все отрезки ища такой, который своим началом стыкуется к последнему найденному и его конечная точка ещё не встречалась среди точек отрезков в массиве, и добавляем его в конец массива.
4. Если конец этого отрезка совпадает с началом первого отрезка массива — значит мы нашли контур — добавляем массив отрезков в массив найденных контуров и выходим из рекурсии.
5. Если нет — рекурсивно вызываем процедуру поиска следующего отрезка.

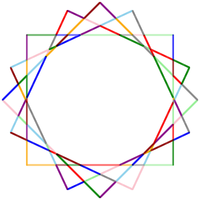Добавив к этому алгоритму процедуру исключения составных контуров можно получить нечто вполне работоспособное. И я думал, что всё хорошо, пока не столкнулся с реальной ситуацией (см. рисунки). Обратите внимание на жёлтую «звезду» на цепи у известного персонажа. Она нарисована наложением множества повёрнутых вокруг своего центра квадратов. После разбиения отрезков по точкам пересечений, первых у нас оказывает аж 112 штук. Дождаться окончания процедуры поиска контуров на этом изображении мне не удалось. А ведь действительно, оценка времени подобного перебора от количества отрезков составляет O(n!), что как вы понимаете, нормально для десятка отрезков, но совершенно неприемлемо для сотни. Мне пришлось подумать над другим алгоритмом.

Направленный поиск выбором «крайнего» отрезка

Давайте вернёмся к исходному рисунку (он продублирован слева). Если мы в поисках очередного отрезка для будущего контура пришли по вектору из точки B в точку F, то двигаться дальше имеет смысл либо в точку D, либо в точку G, т.к. двигаясь по вектору FE мы заведомо выберем отрезок, принадлежащий составному контуру! Т.е. как минимум, мы уже можем сильно уменьшить перебор (из каждой точки мы можем пойти максимум двумя путями). И это хорошо, но давайте думать дальше. Заметим, что приведённый выше алгоритм перебора находит все контуры два раза (один раз — двигаясь по часовой стрелке, а другой раз — когда идёт по отрезкам против часовой стрелки). Что если в каждом ветвлении мы будем выбирать только самый крайний в смысле движения по часовой стрелке отрезок? (В примере: если последний вектор-отрезок был BF, то следующий будет FD.) Мы найдём все нужные контуры! Без рекурсии! Чудеса!

Тут стоит упомянуть, что хотя мы идём по часовой стрелке, иногда мы будем находить и контуры с левым обходом (против часовой стрелки), если стартовый вектор-отрезок не принадлежит ни одному контуру с правым обходом. Причём эти левые контуры могут быть составными (На рисунке: вектор AB принадлежит правому контуру ABFDC, а вот вектор BA — составному левому контуру BACDGF.) А значит, нам потребуется исключить все левые контуры из результирующего массива.

Вот как определить, является ли контур правым (здесь (x1,y2) — начальная точка отрезка, (x3,y3) — конечная):

function isClockwise()
{
	var sum = 0.0;
	for (edge in edges)
	{
		sum += (edge.x3 - edge.x1) * (edge.y3 + edge.y1);
	}
	return sum >= 0;
}

Получившийся алгоритм работает уже с приемлемой скоростью (порядка O(n^2), на сколько я понимаю; поправьте, если ошибаюсь) и отлично себя показывает на реальных задачах. А мы идём дальше.

Выявление полигонов по найденным контурам

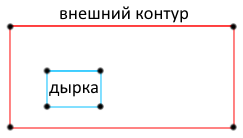Итак, контуры у нас есть. Пора сложить их в полигоны (вспомним, что полигон — это внешний контур + набор внутренних контуров-«дырок»). Задача хорошо решается «в лоб»:

1. Берём последовательно каждый контур за внешний контур будущего полигона.
2. Среди оставшихся контуров ищем те, которые лежат внутри нашего внешнего контура.
3. Берём точку, лежащую внутри внешнего контура, но за пределами его «дырок».
4. На исходном изображении берём заливку в данной точке (т.е. ищем полигон, которому она принадлежит) и если такой полигон находится — добавляем внешний контур+«дырки» как новый полигон в массив найденных для исходного изображения.
5. Аналогично для конечного изображения (ищем полигон, которому принадлежит точка и если находится — добавляем новый полигон в массив найденных для конечного изображения).

Таким образом мы «реконструируем» исходное и конечное изображение после пересечения всех отрезков. Причём теперь мы гарантированно имеем, что каждый из полигонов исходного изображения либо совпадает (в смысле координат) с таким же полигоном накладываемого изображения, либо выступает за пределы всех его полигонов.

Думаю, стоит обратить особое внимание на п.3. Как взять хорошую точку внутри контура за пределами его внутренних контуров? Для начала, нам нужно понимать, что точка тогда лежит внутри полигона, когда выпущенный из неё в любом направлении луч пересекается с отрезками полигона нечётное число раз. И всё бы хорошо, только вот из-за ограниченной точности вычислений луч может попасть в место соединения отрезков, что может вызвать казусы (детектирование пересечений с обоими отрезками, либо с одним, либо ни с одним вообще). Чаще всего, для упрощения вычислений, луч выпускают горизонтально. Также будем делать и мы. Вот что мы теперь знаем о хорошей точке:

• она не должна совпадать ни с одним из концов отрезков, составляющих полигон (и чем больше не совпадает — тем лучше);
• желательно, чтобы точка лежала подальше от отрезков полигона, чтобы уменьшить вероятность проблем, связанных с детектированием пересечений выпущенного из неё луча с этими самыми отрезками.

В голову приходит следующий алгоритм поиска координаты y для такой точки:

1. Загоняем в массив все y-координаты концов отрезков, составляющих полигон.
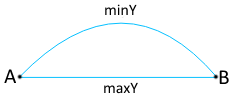2. Добавляем в него minY и maxY нашего внешнего контура (т.к. эти значения не всегда совпадают со значениями в концах отрезков — см. рис. справа).
3. Сортируем массив по возрастанию.
4. Ищем в массиве последовательную пару значений (y1,y2) для которых разность y2 — y1 максимальна.
5. Принимаем среднее арифметическое этих значений за координату y искомой точки: y = (y1 + y2) / 2.

Осталось найти удобное нам значение координаты x. Для этого:

1. Выпускаем горизонтальный луч из точки (-бесконечность; y) вправо.
2. Находим все координаты x точек пересечения луча с отрезками полигона;
3. Сортируем их по возрастанию.
4. Выбираем среди пар (x[i], x[i+1]), где i=0,2,4... такую, для которой разница x[i+1] — x[i] максимальна.
5. Берём среднее арифметическое этой пары за значение координаты x искомой точки: x = (x[i] + x[i+1]) / 2.

Полученный алгоритм не идеален, но достаточно прост и, как показывает практика, хорошо работает на реальных задачах.

Последние шаги

В рамках статьи мы не будем рассматривать подробно оставшиеся пункты алгоритма поиска объединения изображений:

• удаление всех рёбер исходного изображения, которые целиком попали внутрь закрашенных областей накладываемого изображения;
• удаление из исходного изображения всех полигонов, имеющихся в накладываемом изображении без учёта цвета;
• добавление к рёбрам и полигонам исходного изображения всех рёбер и полигонов накладываемого изображения (при этом совпадающие рёбра исходного изображения затираются рёбрами накладываемого);
• объединение на исходном изображении примыкающих друг к другу полигонов, имеющих одинаковую закраску и не имеющих явного разделения рёбрами.

Полагаю, что эти подзадачи достаточно тривиальны и читатели без труда (при необходимости) разберутся с этим самостоятельно.

Заключение

В статье я постарался показать ряд интересных моментов, связанных с поиском объединения векторных изображений. Некоторые особенности остались за кадром, т.к. они либо слишком мелкие, либо автор просто про них забыл. Буду рад любым уточнениям как по статье, так и по описанным алгоритмам.