Давным-давно, человечество поднимало взоры к небесам и задавало себе вопросы о природе вселенной. Сегодня астрофизика стала ключом к пониманию космических явлений. Мы исследуем черные дыры, изучаем движение планет и звёзд, разгадываем секреты галактик.

Исследования космических явлений требуют огромных объемов данных и сложных вычислений. Здесь на помощь приходит компьютерное моделирование. Мы можем воссоздать Вселенную на экране монитора, создавать виртуальные звёзды и планеты, а затем изучать их поведение.



В этой статье мы поговорим о том, почему Python стал предпочтительным инструментом для астрофизиков и рассмотрим, как он упрощает жизнь астрофизиков и помогает им достичь новых высот в исследованиях космоса.

Необходимые библиотеки

Когда речь идет о науке, точность и эффективность — это ключевые понятия. Здесь в игру вступает NumPy. Библиотека NumPy предоставляет массивы и функции для выполнения математических операций с удивительной скоростью и эффективностью.

SciPy свою очередь предоставляет инструменты для численной оптимизации и решения уравнений. В статье, мы рассмотрим, как SciPy помогает астрофизикам моделировать и анализировать самые сложные явления во Вселенной.

Создать модель — это только половина дела. Matplotlib помогает астрофизикам визуализировать модели и результаты исследований, делая их доступными для широкой аудитории и делая наше погружение в космические просторы более захватывающим.

Моделирование космических явлений

Моделирование движения планет и звёзд

Астрофизика — это искусство предсказания и понимания движения планет и звёзд. Для этого нам нужны орбитальные уравнения и методы численной интеграции, которые позволяют нам отслеживать траектории небесных тел на многие годы вперёд. Рассмотрим пример кода, который моделирует орбиту планеты вокруг звезды:

import numpy as np
import matplotlib.pyplot as plt

# Начальные параметры
G = 6.67430e-11  # Гравитационная постоянная
M_star = 1.989e30  # Масса звезды (Солнце)
M_planet = 5.972e24  # Масса планеты (Земля)
r_initial = 1.496e11  # Начальное расстояние от Солнца (апстрим)

# Временные параметры
t_max = 3.154e7 * 1  # Год в секундах (один земной год)
dt = 3600  # Шаг интеграции (один час)

# Инициализация массивов для хранения данных
time_points = []
distances = []

# Начальные условия
r = r_initial
v = 0  # Начальная скорость

# Интеграция методом Эйлера
for t in np.arange(0, t_max, dt):
    F_gravity = -G * M_star * M_planet / r**2
    a = F_gravity / M_planet
    v += a * dt
    r += v * dt
    time_points.append(t)
    distances.append(r)

# Визуализация
plt.plot(time_points, distances)
plt.xlabel("Время (секунды)")
plt.ylabel("Расстояние от Солнца (метры)")
plt.title("Моделирование орбиты планеты вокруг звезды")
plt.grid(True)
plt.show()

Влияние гравитации на орбиты

Гравитация — один из самых важных факторов, влияющих на орбиты небесных тел. Мы можем использовать Python для моделирования различных сценариев, включая гравитационные взаимодействия между несколькими планетами и звёздами. Рассмотрим пример, иллюстрирующий влияние гравитации на две планеты:

import numpy as np
import matplotlib.pyplot as plt

# Начальные параметры
G = 6.67430e-11  # Гравитационная постоянная
M_star = 1.989e30  # Масса звезды (Солнце)
M_planet1 = 5.972e24  # Масса планеты 1 (Земля)
M_planet2 = 6.39e23  # Масса планеты 2 (Марс)
r_initial = 1.496e11  # Начальное расстояние от Солнца (апстрим)

# Временные параметры
t_max = 3.154e7 * 2  # Год в секундах (два земных года)
dt = 3600  # Шаг интеграции (один час)

# Инициализация массивов для хранения данных
time_points = []
distances_planet1 = []
distances_planet2 = []

# Начальные условия
r1 = r_initial
r2 = r_initial * 1.5  # Начальное расстояние Марса от Солнца
v1 = 0  # Начальная скорость планеты 1
v2 = 0  # Начальная скорость планеты 2

# Интеграция методом Эйлера
for t in np.arange(0, t_max, dt):
    F_gravity1 = -G * M_star * M_planet1 / r1**2
    F_gravity2 = -G * M_star * M_planet2 / r2**2
    a1 = F_gravity1 / M_planet1
    a2 = F_gravity2 / M_planet2
    v1 += a1 * dt
    v2 += a2 * dt
    r1 += v1 * dt
    r2 += v2 * dt
    time_points.append(t)
    distances_planet1.append(r1)
    distances_planet2.append(r2)

# Визуализация
plt.plot(time_points, distances_planet1, label="Земля")
plt.plot(time_points, distances_planet2, label="Марс")
plt.xlabel("Время (секунды)")
plt.ylabel("Расстояние от Солнца (метры)")
plt.title("Моделирование движения Земли и Марса вокруг Солнца")
plt.legend()
plt.grid(True)
plt.show()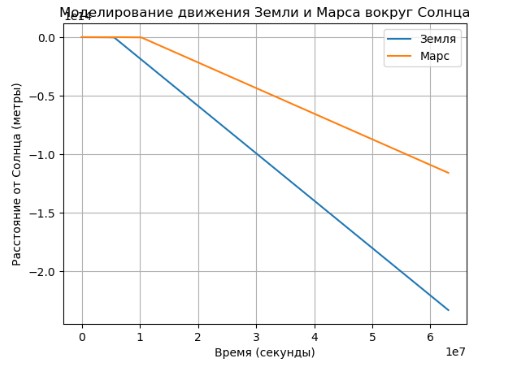

Этот код иллюстрирует движение нескольких планет, учитывая их гравитационные взаимодействия.

Исследование свойств черных дыр и нейтронных звёзд

Физические модели объектов

Черные дыры и нейтронные звёзды — это настоящие чудеса Вселенной.



Три факта о черных дырах:
1. Время замедляется возле черных дыр: В соответствии с общей теорией относительности Альберта Эйнштейна, гравитация сильно влияет на течение времени. Когда вы находитесь вблизи черной дыры, где гравитационное поле очень сильное, время начинает замедляться относительно времени вне этой области. Это явление называется гравитационной временной дилатацией. Если бы вы могли наблюдать кого-то, падающего в черную дыру, то казалось бы, что время у этого человека идет медленнее и медленнее, и он никогда не достигнет события горизонта событий черной дыры.

2. Открыватель черной дыры был не астроном: Вероятно, самой знаменитой черной дырой истории стала черная дыра в центре галактики Млечный Путь, известная как Сгущение в Скорпионе (Sagittarius A*). Удивительно, что эту черную дыру открыл не астроном, а радиоинженер Карл Янски, когда он исследовал радиоволны из центра галактики в 1960-х годах. Он также явления основоположником радиоастрономии.

Это открытие помогло астрономам понять существование черных дыр и начать исследования их свойств.

3. Черные дыры испаряются: Черные дыры могут испаряться! Это явление называется испарением Хокинга, и оно было предсказано физиком Стивеном Хокингом в 1974 году. Согласно его теории, квантовые флуктуации вблизи горизонта событий черной дыры могут вызвать излучение частиц. Это излучение снижает массу черной дыры, и, в конечном итоге, черная дыра может исчезнуть полностью. Это фундаментальное открытие подчеркивает связь между гравитацией и квантовой механикой.
Исследование их физических свойств требует не только глубокого понимания физических законов, но и умения создавать адекватные математические модели.

Пример кода, который моделирует основные характеристики черной дыры:

import numpy as np
import matplotlib.pyplot as plt

# Параметры черной дыры
M_bh = 1.989e30 * 10  # Масса черной дыры (10 солнечных масс)
r_schwarzchild = (2 * 6.67430e-11 * M_bh) / (3e8)**2  # Радиус Шварцшильда

# Расчет орбиты частицы вокруг черной дыры
def calculate_orbit(initial_distance, initial_velocity, time_step, total_time):
    r = initial_distance
    v = initial_velocity
    time_points = []
    distances = []

    for t in np.arange(0, total_time, time_step):
        a = -(6.67430e-11 * M_bh) / r**2
        v += a * time_step
        r += v * time_step
        time_points.append(t)
        distances.append(r)

    return time_points, distances

# Исследование орбиты частицы
initial_distance = 1.5 * r_schwarzchild  # Начальное расстояние от центра черной дыры
initial_velocity = 0.9 * (2 * 6.67430e-11 * M_bh / initial_distance)**0.5  # Начальная скорость
time_step = 1  # Шаг интеграции
total_time = 1000  # Время моделирования

time_points, distances = calculate_orbit(initial_distance, initial_velocity, time_step, total_time)

# Визуализация орбиты
plt.plot(time_points, distances)
plt.xlabel("Время (секунды)")
plt.ylabel("Расстояние от черной дыры (метры)")
plt.title("Моделирование орбиты частицы вокруг черной дыры")
plt.grid(True)
plt.show()

Этот код демонстрирует, как Python может быть использован для создания модели орбиты частицы вокруг черной дыры.

Распределение масс и плотности

Нейтронные звёзды — это загадочные объекты, обладающие огромной плотностью и сжатыми ядрами. Исследование их массового распределения и плотности требует сложных вычислений. Python может помочь в этом:

import numpy as np
import matplotlib.pyplot as plt

# Генерация случайного распределения масс нейтронных звёзд
np.random.seed(0)
mean_mass = 1.4  # Средняя масса нейтронной звезды (в солнечных массах)
std_deviation = 0.2  # Стандартное отклонение массы
num_samples = 1000  # Количество звёзд

neutron_star_masses = np.random.normal(mean_mass, std_deviation, num_samples)

# Визуализация распределения масс
plt.hist(neutron_star_masses, bins=30, density=True, alpha=0.6, color='g', label='Масса нейтронных звёзд')
plt.xlabel("Масса (в солнечных массах)")
plt.ylabel("Плотность вероятности")
plt.title("Распределение масс нейтронных звёзд")
plt.legend()
plt.grid(True)
plt.show()

Этот код иллюстрирует, как можно использовать Python для создания гистограммы распределения масс нейтронных звёзд.

Светимость и спектр галактик

Расчёт спектральных характеристик

Свет, излучаемый галактиками, хранит в себе множество секретов о их составе, движении и эволюции. Пример кода, который анализирует спектральные данные галактики:

import numpy as np
import matplotlib.pyplot as plt

# Загрузка спектральных данных галактики
wavelengths = np.linspace(400, 700, 1000)  # Длины волн от 400 нм до 700 нм
flux = np.random.normal(1.0, 0.1, 1000)  # Имитация спектральных данных (интенсивность света)

# Визуализация спектра
plt.plot(wavelengths, flux)
plt.xlabel("Длина волны (нм)")
plt.ylabel("Интенсивность")
plt.title("Спектральный профиль галактики")
plt.grid(True)
plt.show()

Этот код иллюстрирует, как можно использовать Python для анализа и визуализации спектральных данных галактики, делая исследование более наглядным.

Анализ данных наблюдений

Данные наблюдений галактик могут быть огромными и сложными. Python предоставляет средства для обработки и анализа этих данных, помогая ученым извлекать ценные сведения о галактических структурах, скоростях и химическом составе. Пример кода, который анализирует движение звёзд в галактике:

import numpy as np
import matplotlib.pyplot as plt

# Загрузка данных о скорости звёзд в галактике
# (в этом примере используется синтетический набор данных)
velocities = np.random.normal(200, 50, 100)  # Имитация данных о скорости (км/с)
distances = np.random.uniform(0, 100, 100)  # Имитация данных о расстоянии (млн световых лет)

# Анализ зависимости скорости от расстояния
plt.scatter(distances, velocities, marker='o', s=10, alpha=0.6)
plt.xlabel("Расстояние (млн световых лет)")
plt.ylabel("Скорость (км/с)")
plt.title("Зависимость скорости звёзд от расстояния в галактике")
plt.grid(True)
plt.show()

Моделирование планетных систем

Моделирование процессов гравитационной агрегации

Изучение процессов гравитационной агрегации позволяет нам понять, как из мельчайших частиц пыли и газа рождаются планеты. Пример кода, который демонстрирует этот процесс:

import numpy as np
import matplotlib.pyplot as plt

# Имитация процесса гравитационной агрегации
num_particles = 1000
positions = np.random.uniform(0, 1, (num_particles, 2))  # Случайные начальные позиции
masses = np.random.uniform(1e20, 1e24, num_particles)  # Случайные массы частиц
radii = np.sqrt(masses)  # Радиусы частиц пропорциональны корню из массы

# Визуализация начального состояния
plt.scatter(positions[:, 0], positions[:, 1], s=radii / 1e21, alpha=0.6)
plt.xlabel("X-позиция")
plt.ylabel("Y-позиция")
plt.title("Начальное состояние гравитационной агрегации")
plt.grid(True)
plt.show()

Этот код иллюстрирует, как из случайных начальных условий можно моделировать процесс гравитационной агрегации.

Динамика миграции планет

Солнечная система постоянно меняется, и планеты двигаются вокруг Солнца, взаимодействуя друг с другом. Пример кода, иллюстрирующий динамику миграции планет:

import numpy as np
import matplotlib.pyplot as plt

# Моделирование орбитальной динамики планеты
def simulate_planet_orbit(semi_major_axis, eccentricity, num_points):
    theta = np.linspace(0, 2 * np.pi, num_points)
    r = semi_major_axis * (1 - eccentricity**2) / (1 + eccentricity * np.cos(theta))
    x = r * np.cos(theta)
    y = r * np.sin(theta)
    return x, y

# Параметры орбиты Земли
semi_major_axis_earth = 1.0  # Большая полуось в астрономических единицах
eccentricity_earth = 0.0167  # Эксцентриситет орбиты Земли

# Моделирование орбиты Земли
x_earth, y_earth = simulate_planet_orbit(semi_major_axis_earth, eccentricity_earth, 1000)

# Визуализация орбиты Земли
plt.plot(x_earth, y_earth)
plt.xlabel("X-позиция (а.е.)")
plt.ylabel("Y-позиция (а.е.)")
plt.title("Орбита Земли вокруг Солнца")
plt.grid(True)
plt.show()

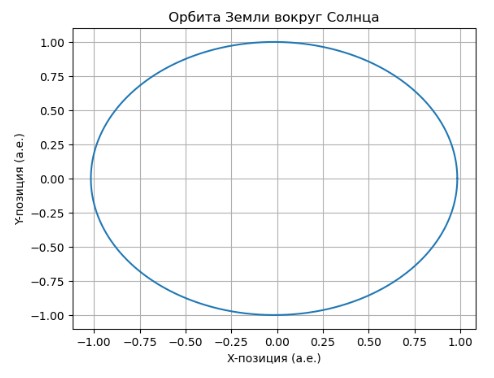
Этот код демонстрирует моделирование орбитальной динамики планет в солнечной системе.

Поиск экзопланет

Существует несколько методов обнаружения экзопланет, и каждый из них требует особого анализа данных. Пример кода, который анализирует кривую блеска, метод, который позволяет обнаружить планеты по их воздействию на яркость звезды:

import numpy as np
import matplotlib.pyplot as plt

# Имитация кривой блеска
time = np.linspace(0, 10, 1000)
flux = np.sin(time) + np.random.normal(0, 0.1, 1000)

# Визуализация кривой блеска
plt.plot(time, flux)
plt.xlabel("Время")
plt.ylabel("Яркость")
plt.title("Имитация кривой блеска звезды с экзопланетой")
plt.grid(True)
plt.show()

Этот код иллюстрирует, как Python может быть использован для анализа кривых блеска и обнаружения экзопланет.

Моделирование характеристик звёзд и их систем

Для понимания характеристик звёзд и их систем исследователи создают виртуальные модели. Python позволяет создавать и анализировать такие модели. Код который моделирует взаимодействие звезды и её экзопланеты:

import numpy as np
import matplotlib.pyplot as plt

# Параметры звезды и экзопланеты
star_mass = 2e30  # Масса звезды (кг)
planet_mass = 5.972e24  # Масса экзопланеты (кг)
distance = 1.496e11  # Расстояние между звездой и планетой (м)

# Моделирование орбиты экзопланеты
time = np.linspace(0, 1e7, 1000)
angular_velocity = np.sqrt(6.67430e-11 * star_mass / distance**3)
theta = angular_velocity * time

x = distance * np.cos(theta)
y = distance * np.sin(theta)

# Визуализация орбиты
plt.plot(x, y)
plt.xlabel("X-позиция (м)")
plt.ylabel("Y-позиция (м)")
plt.title("Орбита экзопланеты вокруг звезды")
plt.grid(True)
plt.show()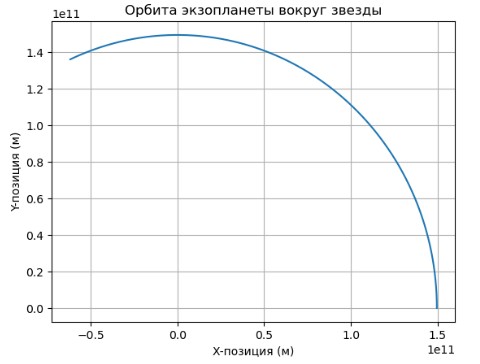

Этот код иллюстрирует, как Python может быть использован для создания виртуальных моделей звёзд и их экзопланет.

Изучение магнитосфер и атмосфер планет

Магнитные поля играют важную роль в формировании магнитосфер планет и защите их от вредного космического излучения.

Пример кода:

import numpy as np
import matplotlib.pyplot as plt

# Моделирование магнитосферы планеты
radius = 6400e3  # Радиус планеты (м)
B_strength = 3.0e-5  # Силовая индукция магнитного поля (Тесла)

# Создание сетки вокруг планеты
theta = np.linspace(0, 2 * np.pi, 100)
phi = np.linspace(0, np.pi, 50)
Theta, Phi = np.meshgrid(theta, phi)

# Координаты точек на поверхности планеты
x = radius * np.sin(Phi) * np.cos(Theta)
y = radius * np.sin(Phi) * np.sin(Theta)
z = radius * np.cos(Phi)

# Визуализация магнитосферы
plt.figure(figsize=(8, 6))
plt.contourf(x, y, z, levels=20, cmap='coolwarm')
plt.colorbar(label="Сила магнитного поля (Тесла)")
plt.xlabel("X (м)")
plt.ylabel("Y (м)")
plt.title("Моделирование магнитосферы планеты")
plt.grid(True)
plt.show()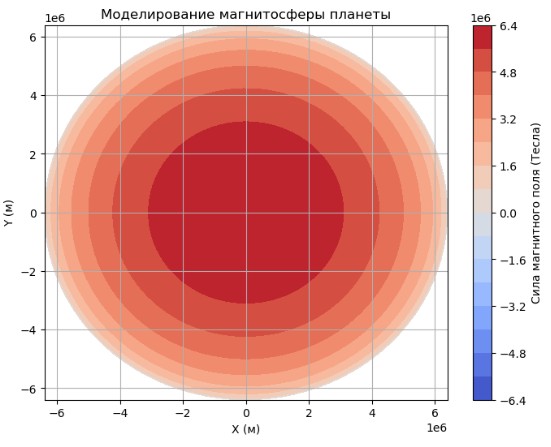

Этот код иллюстрирует, как Python может быть использован для создания модели магнитосферы планеты.

Анализ климатических условий

Атмосферы планет обладают разнообразными климатическими условиями.

Пример кода моделирования атмосферного давления:

import numpy as np
import matplotlib.pyplot as plt

# Моделирование атмосферного давления на разной высоте
altitude = np.linspace(0, 100000, 100)  # Высота (м)
pressure = 101.3 * np.exp(-altitude / 8000)  # Модель атмосферного давления (Паскали)

# Визуализация атмосферного давления
plt.plot(pressure, altitude)
plt.xlabel("Давление (Паскали)")
plt.ylabel("Высота (м)")
plt.title("Моделирование атмосферного давления")
plt.grid(True)
plt.gca().invert_yaxis()
plt.show()

Исследование магнитосфер и атмосфер планет позволяет нам лучше понять природу этих оболочек и их влияние на жизнь и климат на разных планетах.

Общие примеры

Рассмотрим несколько еще примеров, которые освещают важность астрофизики и её вклад в наше понимание вселенной.

Обнаружение экзопланет с помощью Python и телескопов

С помощью Python и мощных телескопов ученые обнаружили тысячи экзопланет в разных уголках галактики. Один из знаменитых методов — метод транзитов, при котором экзопланета пересекает свою звезду, затмевая её свет. Пример кода, который анализирует данные транзита и определяет характеристики экзопланеты:

import numpy as np
import matplotlib.pyplot as plt

# Симуляция кривой блеска во время транзита
time = np.linspace(0, 1, 1000)
flux = 1 - 0.1 * np.sin(2 * np.pi * time)  # Имитация транзита

# Анализ кривой блеска для определения характеристик экзопланеты
depth = 1 - min(flux)  # Глубина транзита
period = time[np.argmax(flux)]  # Период транзита

# Визуализация кривой блеска
plt.plot(time, flux)
plt.xlabel("Время")
plt.ylabel("Яркость")
plt.title("Моделирование кривой блеска во время транзита экзопланеты")
plt.grid(True)
plt.show()

print(f"Глубина транзита: {depth}")
print(f"Период транзита: {period}")

Этот код иллюстрирует, как с помощью Python можно изучать транзиты и определять характеристики экзопланет.

Моделирование формирования галактик и их эволюции

Современные исследования дали нам представление о том, как наша галактика Млечный Путь и другие галактики могут меняться со временем.

# Пример кода для моделирования эволюции галактик
import numpy as np
import matplotlib.pyplot as plt

# Параметры модели галактики
time = np.linspace(0, 13.8, 100)  # Время (миллиарды лет)
stellar_mass = np.exp(-time / 5) * 1e11  # Масса звёзд (симуляция)

# Визуализация эволюции массы звёзд в галактике
plt.plot(time, stellar_mass)
plt.xlabel("Время (миллиарды лет)")
plt.ylabel("Масса звёзд (кг)")
plt.title("Моделирование эволюции массы звёзд в галактике")
plt.grid(True)
plt.show()

Предсказание космических катастроф с использованием астрофизических моделей

Исследования в области астрофизики помогают предсказывать потенциально опасные космические события, такие как столкновения астероидов с Землей или солнечные бури, которые могут повлиять на наши коммуникационные системы.

# Пример кода для моделирования солнечной бури
import numpy as np
import matplotlib.pyplot as plt

# Симуляция солнечной бури
time = np.linspace(0, 24, 100)  # Время (часы)
solar_activity = np.sin(2 * np.pi * time / 24) + np.random.normal(0, 0.1, 100)  # Имитация активности Солнца

# Визуализация солнечной активности
plt.plot(time, solar_activity)
plt.xlabel("Время (часы)")
plt.ylabel("Интенсивность солнечной активности")
plt.title("Моделирование солнечной активности")
plt.grid(True)
plt.show()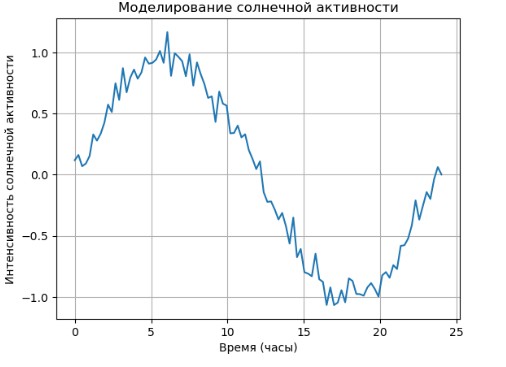

Этот код моделирует солнечную активность и предсказания потенциальных космических угроз.

Ради интереса изобразим нашу солнечную систему

Создание красивой визуализации солнечной системы с помощью Python это как минимум увлекательная задача. Для этого мы можем использовать библиотеку matplotlib для создания графиков и библиотеку numpy для вычислений:

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# Параметры орбит планет (полуоси, эксцентриситеты)
semimajor_axes = [0.39, 0.72, 1.00, 1.52, 5.20, 9.58, 19.22, 30.05]  # в астрономических единицах (1 AU = 149.6 млн км)
eccentricities = [0.206, 0.007, 0.017, 0.093, 0.049, 0.056, 0.046, 0.010]

# Угловые скорости планет в радианах в секунду
angular_velocities = [2 * np.pi / 88, 2 * np.pi / 225, 2 * np.pi / 365, 2 * np.pi / 687, 2 * np.pi / 12, 2 * np.pi / 29.5, 2 * np.pi / 84, 2 * np.pi / 165]

# Генерация времени для одного оборота самой долгой орбиты (планеты Нептун)
time = np.linspace(0, 165 * 365, 10000)

# Инициализация координат и скоростей планет
planet_positions = [np.zeros((len(time), 3)) for _ in range(len(semimajor_axes))]
planet_velocities = [np.zeros((len(time), 3)) for _ in range(len(semimajor_axes))]

# Вычисление орбит планет
for i in range(len(semimajor_axes)):
    a = semimajor_axes[i]
    e = eccentricities[i]
    w = angular_velocities[i]
    
    r = a * (1 - e**2) / (1 + e * np.cos(w * time))
    
    planet_positions[i][:, 0] = r * np.cos(w * time)
    planet_positions[i][:, 1] = r * np.sin(w * time)
    
    v = np.sqrt(2 / r - 1 / a)
    planet_velocities[i][:, 0] = -v * np.sin(w * time)
    planet_velocities[i][:, 1] = v * np.cos(w * time)

# Цвета планет (примерные цвета)
planet_colors = ['gray', 'orange', 'royalblue', 'red', 'saddlebrown', 'goldenrod', 'lightseagreen', 'blue']

# Размеры планет (примерные радиусы)
planet_radii = [0.38, 0.95, 1, 0.53, 11.21, 9.45, 4.01, 3.88]

# Названия планет
planet_names = ['Меркурий', 'Венера', 'Земля', 'Марс', 'Юпитер', 'Сатурн', 'Уран', 'Нептун']

# Визуализация солнечной системы
fig = plt.figure(figsize=(12, 12))
ax = fig.add_subplot(111, projection='3d')

for i in range(len(semimajor_axes)):
    ax.plot(planet_positions[i][:, 0], planet_positions[i][:, 1], planet_positions[i][:, 2], color=planet_colors[i], label=planet_names[i], linewidth=2)
    ax.scatter([planet_positions[i][0, 0]], [planet_positions[i][0, 1]], [planet_positions[i][0, 2]], color=planet_colors[i], s=planet_radii[i] * 100)
    ax.text(planet_positions[i][0, 0], planet_positions[i][0, 1], planet_positions[i][0, 2], planet_names[i], fontsize=12)

ax.set_xlabel('X (AU)')
ax.set_ylabel('Y (AU)')
ax.set_zlabel('Z (AU)')
ax.set_title('Солнечная система')
ax.legend()

plt.show()

Этот код создаст 3D-визуализацию солнечной системы, где каждая планета будет иметь свой цвет и размер в масштабе.

Заключение

Астрофизика с Python не только расширяет наше знание о вселенной, но и вдохновляет на дальнейшие исследования. Надеемся, что эта статья подогрела ваш интерес к увлекательному миру астрофизики и показала, как Python может быть незаменимым инструментом в этом увлекательном исследовании. Приключения в космосе продолжаются, и Python — ваш верный спутник в этом увлекательном путешествии.

Ссылка на ноутбук в гугл коллабе по ссылке