В данной статье я постараюсь рассказать каким образом можно реализовать движение объектов (далее частиц) по поверхности 3D геометрии.

1. Создание частиц

Для расположения частиц на модели мы будем выбирать случайный треугольник из списка полигонов. Для этого можно использовать следующие методы:

1. Если модель представлена списком вершин, то генерируем случайное число в интервале [0; кол-во вершин / 3 - 1]. Таким образом мы получим индекс первой вершины нужного нам треугольника, а остальные две вершины получим инкрементом индекса на 1 и 2.

2. Если модель представлена списком вершин и индексов, то генерируем случайное число в интервале [0; кол-во индексов / 3 - 1]. Таким образом мы получим индекс первого индекса нужного нам треугольника, а остальные два индекса получим инкрементом на 1 и 2. Из списка вершин мы достаем нужные нам вершины по рассчитанным индексам.

После выбора треугольника нам необходимо расположить частицу внутри него, используя барицентрические координаты (Рисунок 1).

Барицентрические координаты представляют собой средневзвешенное значение вершин треугольника (P₀, P_1, P₂) и выражаются в виде скаляров w₀, w₁, w₂, таких что:

Точка P лежит внутри треугольника, если все три весовые коэффициенты неотрицательны и их сумма равна 1. Поэтому мы можем сгенерировать первые два коэффициента случайным образом, а третий получить путем вычитания из 1:

Затем мы подставляем вершины выбранного нами треугольника и вычисленные весовые коэффициенты в формулу барицентрических координат.

2. Движение частиц

Для того, чтобы задать скорость частице, необходимо определить вектор скорости, который должен быть параллелен плоскости треугольника и перпендикулярен вектору нормали этой плоскости (Рисунок 2).

Получить такой вектор V можно вычитанием позиции частицы P из позиции одной из трех вершин треугольника (Рисунок 3). Однако, чтобы придать хаотичности движению частиц, необходимо повернуть полученный вектор на случайный угол θ вокруг нормали треугольника.

Для выполнения такого поворота необходимо найти нормаль треугольника через векторное произведение и правило правой руки. 

Затем выполнить векторное произведение нашего вектора скорости V и полученной нормали N (Рисунок 5).

В результате получим два перпендикулярных вектора V и Q, которые лежат в плоскости треугольника и составляют прямоугольную систему координат (Рисунок 6).

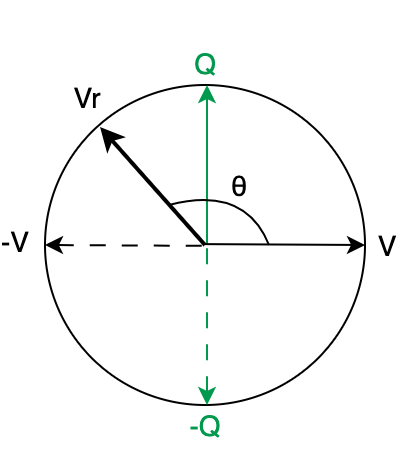
Любой вектор в плоскости треугольника можно выразить как линейную комбинацию векторов V и Q:

где θ - случайный угол поворота.

3. Проверка вхождения в треугольник

В процессе движения частица может выйти за пределы треугольника (Рисунок 7).

Чтобы определить это событие, можно использовать барицентрические координаты. Для этого перепишем формулу барицентрических координат в виде матричного уравнения:

Здесь w₀, w₁ и w₂ - весовые коэффициенты, которые определяют положение точки P относительно треугольника. Чтобы найти эти коэффициенты, нужно инвертировать матрицу:

Если все три весовые коэффициенты неотрицательны и их сумма равна 1, то точка лежит внутри треугольника. Если это условие не выполняется, то точка лежит за пределами треугольника, и нужно перевести частицу в следующий треугольник.

4. Переход между треугольниками

Для того, чтобы определить к какому следующему треугольнику привязать частицу, нужно найти ближайшее к частице ребро текущего треугольника. Соседний треугольник, который делит это ребро с текущим треугольником, и будет новым треугольником (Рисунок 8).

Перед вычислением расстояния до ребра, необходимо проверить, что частица находится в пределах ребра (Рисунок 9). 

Для того, чтобы определить выходит частица за пределы ребра или нет,  будем использовать следующий алгоритм:

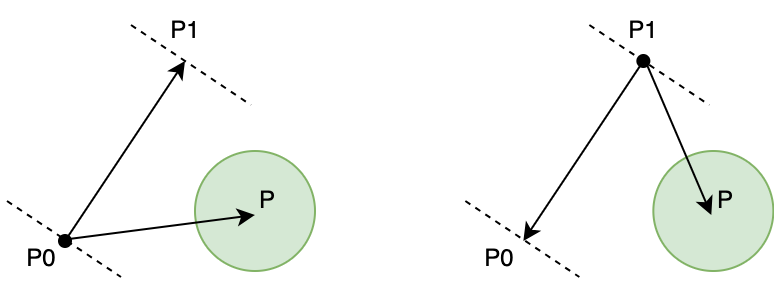
1. Вычисляем векторы P₀P₁ и P₀P, где P₀ и P₁ - координаты концов ребра, а P - координаты частицы.

2. Вычисляем скалярное произведение векторов P₀P₁ и P₀P.

3. Если скалярное произведение меньше нуля, то частица находится за точкой P₀ и не находится в пределах ребра (Рисунок 10). 

4. Вычисляем скалярное произведение векторов P₁P₀ и P₁P.

5. Если скалярное произведение меньше нуля, то частица находится за точкой P₁ и не находится в пределах ребра (Рисунок 11).

6. Если оба скалярных произведения больше нуля, то частица находится в пределах ребра (Рисунок 12).

Для определения вектора смещения частицы к ребру, мы можем спроецировать положение частицы на ребро и построить вектор от позиции частицы к точке проекции.

Формульно это можно выразить следующим образом:

Расстояние d между точкой проекции и частицей можно получить вычислив длину Displacement вектора. Также полученное смещение мы будем использовать, чтобы подвинуть частицу к плоскости треугольника.

Далее необходимо скорректировать движение нашей частицы так, чтобы она двигалась вдоль нового треугольника (Рисунок 14).

Другими словами мы хотим повернуть текущий вектор движения частицы в пространстве таким образом, чтобы он был перпендикулярен нормали нового треугольника. Получается, что нужное нам преобразование вектора движения будет равно преобразованию, которое совершает поворот от первой нормали ко второй (Рисунок 15).

Для выполнения поворота вектора в пространстве мы будем использовать кватернион. Построить кватернион, представляющий вращение вокруг оси на угол , можно следующим образом:

Если учесть, что скалярное и векторное произведение двух нормализованных векторов равны:

то мы можем напрямую построить кватернион, представляющий такое вращение, на основе результатов скалярного и векторного произведения N₀ и N₁. Однако, если посмотреть, как вычисляются компоненты кватерниона, который выполняет поворот на угол , то можно заметить, что используется половина угла . А это означает, что вычисленный нами на основе N₀ и N₁ кватернион будет выполнять поворот в два раза больше, чем нам нужно. Одно из решений состоит в том, чтобы вычислить half-way вектор между N₀ и N₁, и использовать скалярное и векторное произведение N₀ и half-way вектора, чтобы построить нужный нам кватернион.

Также нам нужно обработать два крайних случая прежде, чем вычислять кватернион:

1. Если скалярное произведение N₀ и N₁ равно 1, векторы уже выровнены и вращение не требуется.

2. Если скалярное произведение N₀ и N₁ равно -1, векторы противоположны и требуется поворот на 180 градусов. В этом случае умножаем вектор скорости на -1.

5. Ориентация модели частицы в пространстве

Для корректного отображения модели на сцене необходимо ориентировать ее направление вдоль вектора перемещения V. В данном случае передняя часть модели направлена в противоположную сторону оси Z (Рисунок 17).

Мы можем выполнить эту ориентацию, создав кватернион, который представляет вращение от вектора Forward (-Z), указывающего направление модели, до вектора перемещения. Однако после такого вращения вектор модели UP будет искажен (Рисунок 18).

Нам нужно, чтобы вектор модели UP была параллелен нормали N текущего треугольника (Рисунок 19).

Поэтому мы дополнительно создадим второй кватернион, который выполнит вращение от искаженного вектора UP' к нормали треугольника:

6. Демонстрация

Исходный код

Заключение

Формулы, которые были использованы в статье, вы можете легко освоить, решая задачи на нашем сайте shader-learning.com. 

Shader Learning - это платформа для изучения и практики написания шейдерных программ на OpenGL. Платформа помогает освоить математические модели и техники, которые используются для создания различных эффектов, таких как коррекция цвета, работа с шумом, рейтрейсинг и свет.