Сегодня я расскажу Вам очень показательную историю про одну математическую гипотезу из теории чисел. Она станет ярким примером того, как в математике прерываются, казалось бы, явные закономерности, и что любое предположение в этой науке нуждается в строгом доказательстве, даже если оно проверено для всех чисел, которые только могут поместиться в память суперкомпьютера.

Итак, в 1919 году венгерский математик Дьёрдь Пойя, изучая вопросы, связанные с факторизацией (разложением на простые множители) чисел, выдвинул далеко идущую гипотезу. Суть её такова.
Числа, большие единицы, можно разделить на два класса:
Имеющие нечетное количество множителей в разложении.
Имеющие четное количество множителей в разложении.
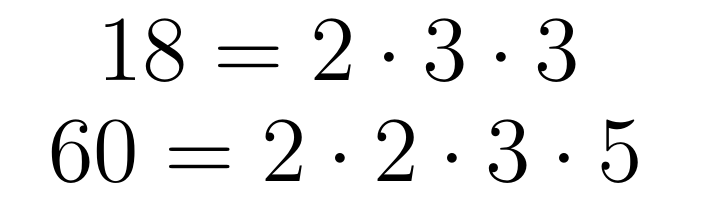
Гипотеза Пойи утверждала, что чисел первого класса не меньше, как далеко бы мы не уходили на бесконечность. Действительно, Пойя проверил данное утверждение и, казалось, тенденция была видна невооруженным глазом.
Впрочем, жизнь любой гипотезы в математике непредсказуема, ведь иногда достаточно всего одного контрпримера, чтобы разрушить её фундамент.
Функция Лиувилля
Гипотеза в том виде, что я показал выше, естественно, требует представления в виде формул и условий, но волноваться из-за этого не стоит.
В теории чисел на каждый особый случай есть своя уникальная функция, да еще и именная.

Функция Луивилля, в общем-то, делает именно то, что нужно для формализации гипотезы Пойи:
принимает значение "1", если у числа чётное количество простых множителей в разложении;
принимает значение "-1" в противном случае.
С использованием функции Лиувилля гипотеза переформулируется следующим образом:
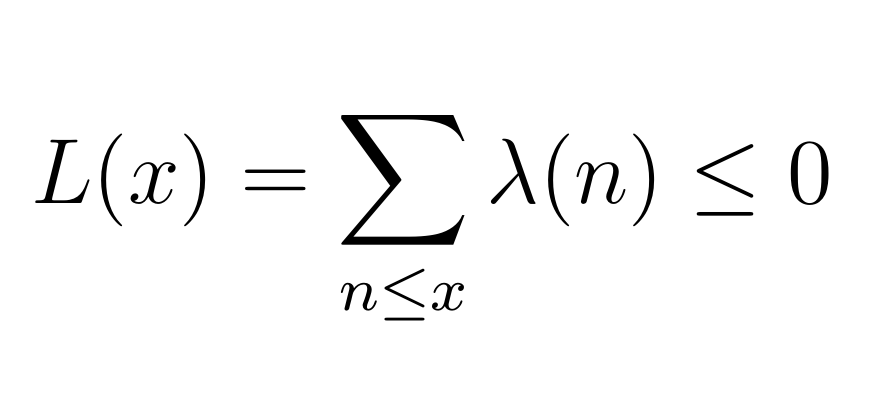
Простейший код для вычисления на Python:
def prime_factors_with_counts(n):
factors = {} # Словарь для хранения простых множителей и их количества
i = 2
while i * i <= n:
if n % i:
i += 1
else:
n //= i
factors[i] = factors.get(i, 0) + 1
if n > 1:
factors[n] = factors.get(n, 0) + 1
return factors
def liouville(n):
factors_with_counts = prime_factors_with_counts(n)
total_factors = sum(factors_with_counts.values())
return 1 if total_factors % 2 == 0 else -1
def cumulative_liouville(n):
cumulative_values = []
cumulative_value = 0
for num in range(1, n + 1):
liouville_result = liouville(num)
cumulative_value += liouville_result
cumulative_values.append(cumulative_value)
return cumulative_values
# Ввод числа N
N = int(input("Введите натуральное число N: "))
if N < 1:
print("Введите число больше или равное 1.")
else:
output_filename = "liouville_table.txt"
with open(output_filename, "w") as file:
file.write("Число | Разложение на простые множители | Функция Луивилля | Кумулятивная Луивилля\n")
file.write("-" * 68 + "\n")
cumulative_values = cumulative_liouville(N)
for num in range(1, N + 1):
factors = prime_factors_with_counts(num)
liouville_result = liouville(num)
cumulative_result = cumulative_values[num - 1]
factors_str = " * ".join([f"{factor}**{count}" if count > 1 else str(factor) for factor, count in factors.items()])
file.write(f"{num:^6} | {factors_str:^36} | {liouville_result:^15} | {cumulative_result:^21}\n")
print(f"Таблица сохранена в файле '{output_filename}'.")Приведенный выше код считает значение функции Лиувилля для каждого числа, вычисляет кумулятивную функцию, а затем выводит результаты в файл. Ниже пример графика для N=250 000 (автор гипотезы вручную проверил все значения до N=1500, а в 1940 году некий индиец "досчитал" до 20 000):
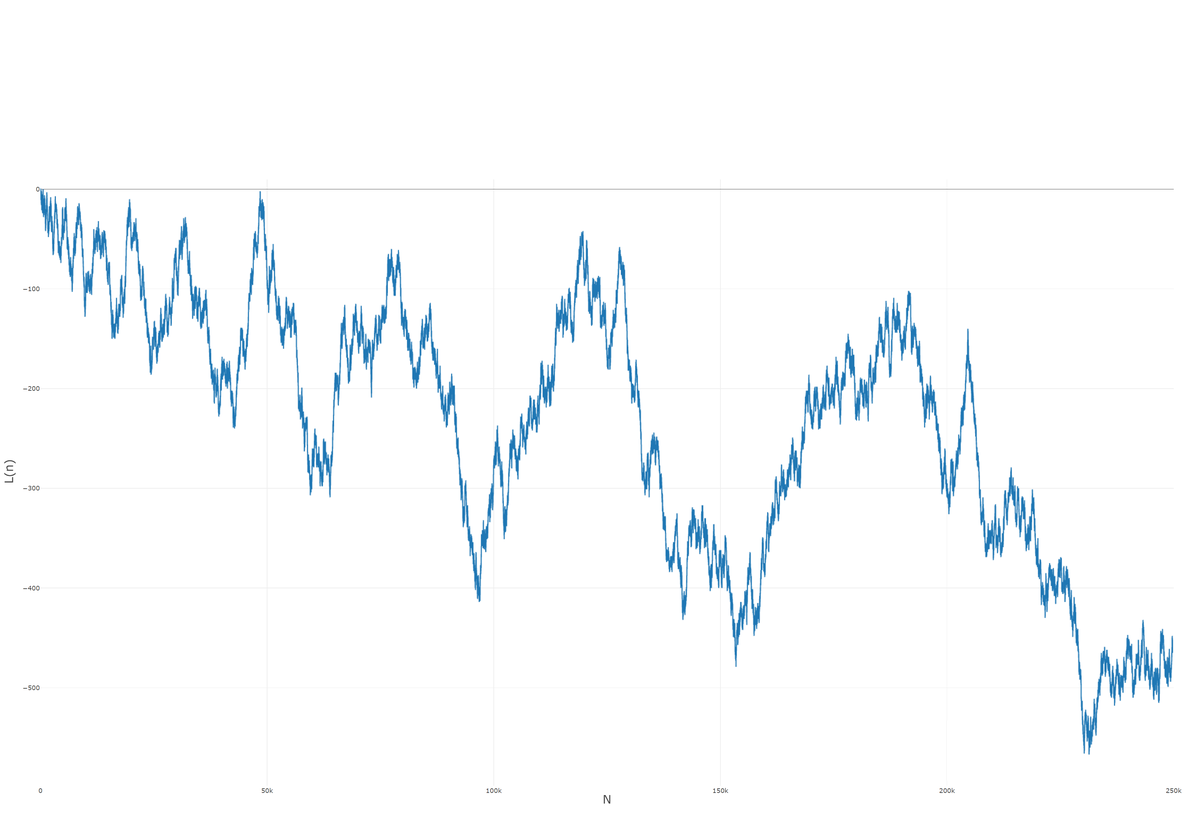
Как мы видим по графику, значения лежат в отрицательной области, да и тренд как бы намекает на ясный статус гипотезы...

В защиту Пойа: гипотезу он взял не просто из головы, а затем проверил на конкретных примерах. Математик изучал квадратичные формы, исследовал решения уравнения L(x) = 0, показал, что в большинстве случаев функция будет отрицательной и перехода через ось абсцисс не будет. Проблема была в том, что он рассмотрел не все возможные варианты.
Кроме того, некоторые источники отмечают, что математик никогда и не предполагал, что это утверждение истинно; скорее, он показал, что истинность утверждения подразумевает гипотезу Римана.
...прошло 40 лет
В 1958 году английский математик Колин Брайан Хазелгроув находит не конструктивный пример, опровергающий гипотезу Пойи. В своей статье он проворачивает довольно интересный приём, используя связь функции Лиувилля с дзета-функцией Римана:
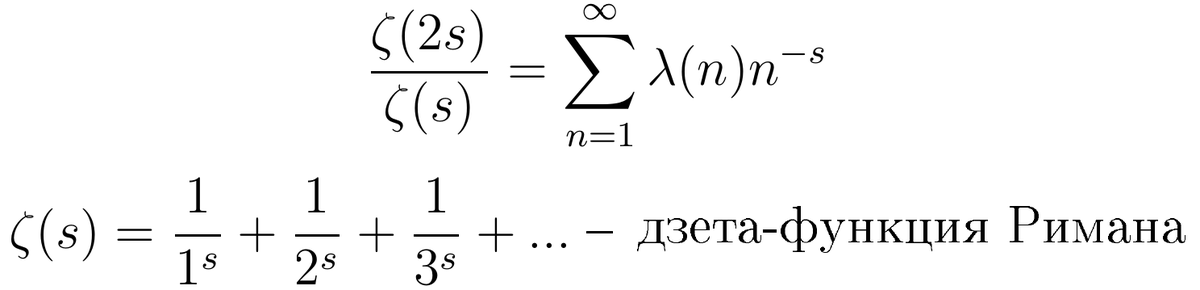
Автор использует введенные еще до него функции (их пытались использовать для доказательства гипотезы Римана), оценив которые, можно сделать вывод о поведении кумулятивной функции Лиувилля:
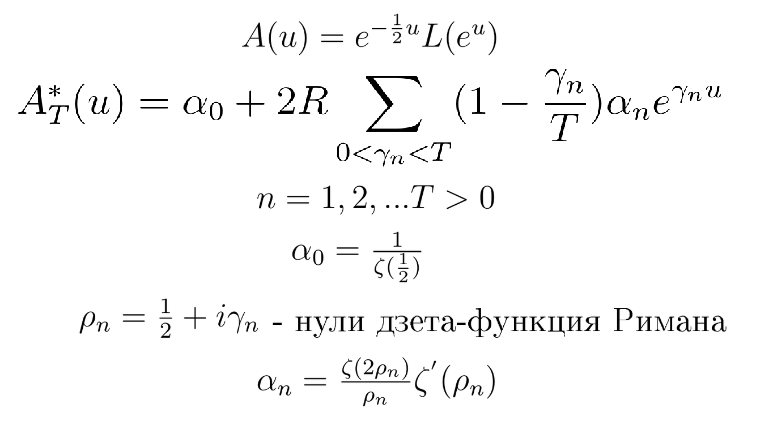
Те же предшественники Хазелгроува показали, что:
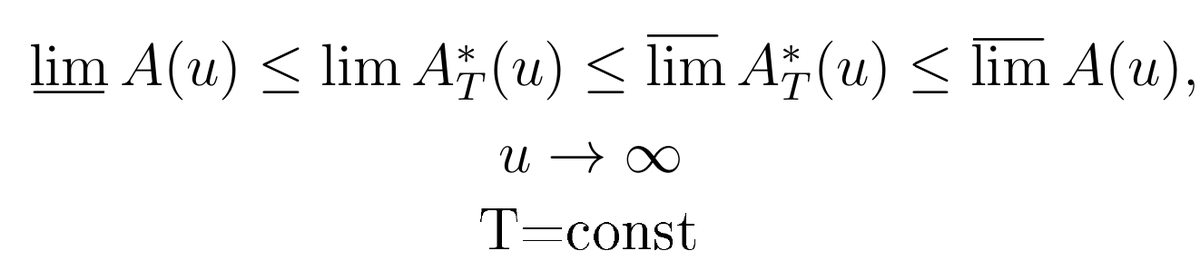
и, что самое главное, что функция А*(T,u) - периодическая! Т.е. у неё есть некоторый диапазон значений:
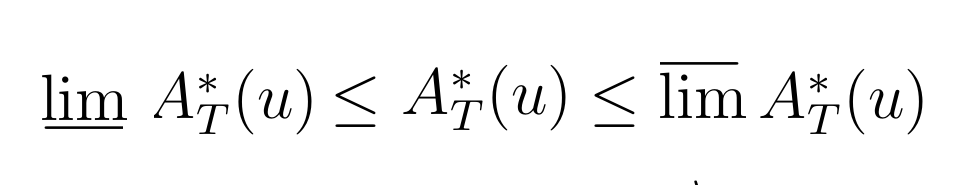
Схематичная иллюстрация выражения выше:

Поэтому, если получится найти Т и u, при которых А*(T,u) > 0, из этого будет следовать
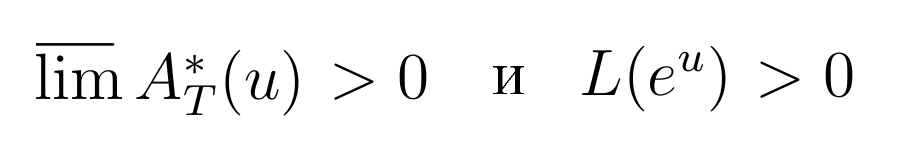
, что приведет к опровержению гипотезы Пойи!
Естественно, Хазелгроув нашёл такие числа. Однако вспомните, что я в начале статьи говорил про неконструктивное доказательство. Англичанин привел не конкретное число, на котором гипотеза "ломается", а некоторый диапазон, где по его расчетам кумулятивная функция Лиувилля поменяет свой знак.
В оригинальной статье приводится Хазелгроув пишет, что они заметили, что наибольший вклад в функцию А*(T,u) вносят первый, второй и седьмой нули дзета-функции Римана. Таким образом при T=1000 удалось "выцепить" набор возможно подходящих значений u:
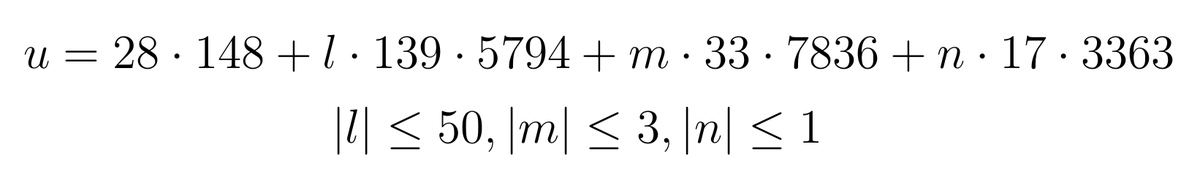
Круг сузился, а расчёты на имевшихся в распоряжении математиков компьютерах EDSAC I и Mark I стали выполнимы за разумное время.

В итоге получили, что переход исследуемой функции, а значит и кумулятивной функции Лиувилля через ось абсцисс должен произойти при 831 < u < 847, что соответствует:
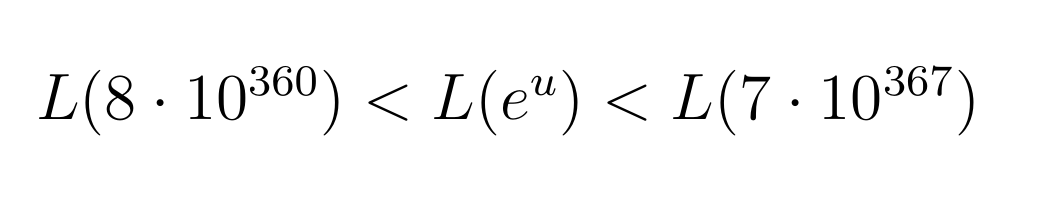
Что ж, по моим данным на этом диапазоне максимальное значение функции было равно:
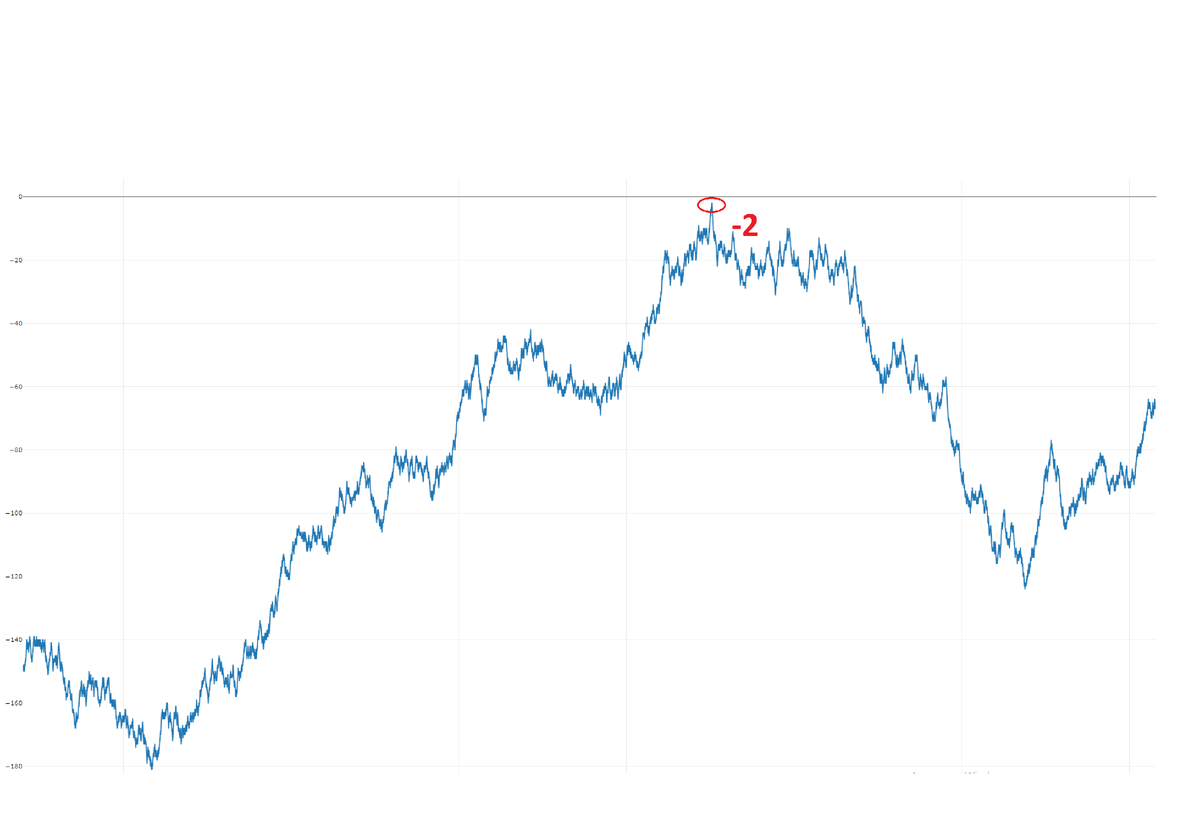
Первый конкретный пример числа, на котором ломается гипотеза Пойи появился в 1960 году. Им стало число 906 180 359, а через 20 лет был найден наименьший на сегодняшний день показатель - 906 150 257. Интересно, что в этом диапазоне функция достигает своего максимального значения в 849:
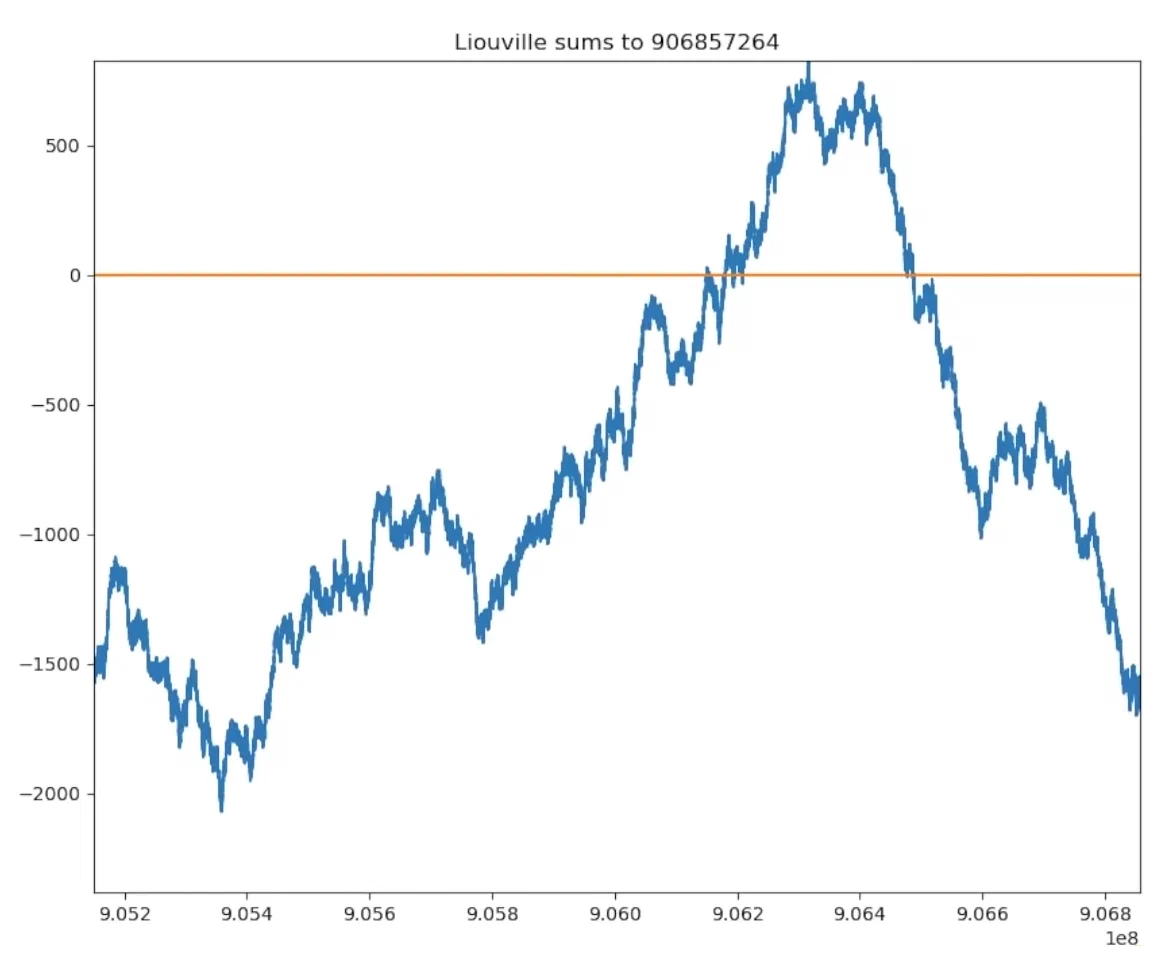
А вот так ведут себя минимумы кумулятивной функции.
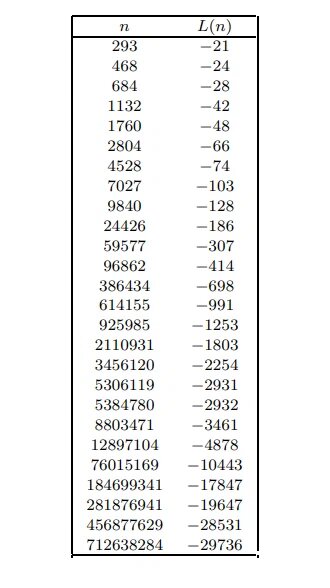
Как Вы понимаете, любители экстраполяции здесь бы не получили результата!

На данный момент гипотеза Пойи еще представляет научный интерес. Во-первых, не ясно, бесконечное ли количество раз кумулятивная функция меняет знак. Во-вторых, у опровергнутой гипотезы еще сохранились "мостики" с гипотезой Римана, истинность которой, к слову, проверена для первых 10 триллионов нетривиальных нулей. Но мы же теперь, не верим на слово?
В Телеграмм " Математика не для всех" доступен архив с оригиналами статей по гипотезе Пойи.
Комментарии (80)

18741878
06.09.2023 15:21Интересно. Но, читая текст, постоянно спотыкался: неужели фамилия "Пойя" склоняется? Странно и довольно не эстетично звучат, на мой взгляд, "Пойи", "Пойе", "Пойю". Знатоки лингвистики, что скажете?
P.S. Есть еще вариант написания фамилии этого математика: "Полиа". В советские времена так и не пришли к общему мнению - как все-таки правильно :) И использовали оба

victor_1212
06.09.2023 15:21+3все просто, фамилия пишется Pólya, но он был из Венгрии, а в венгерском "LY" обычно произносится как "Й",
кстати Pólya был одним из учителей von Neumann в Zürich, кроме прочего интересовался общими подходами при решении математических проблем, есть перевод его книжки - Пойа Д. Как решать задачу (1959), стоит взглянуть

18741878
06.09.2023 15:21+1А все-таки, склоняется "Пойя"/"Пойа"/"Полиа" или нет?

diakin
06.09.2023 15:21+3Мужские фамилии склоняются, женские-нет.

18741878
06.09.2023 15:21+1А вот и не всегда! Славянские "Иванов" и т.п. - склоняются, а "Иваненко" и т.п - уже нет. Далее, не склоняются грузинские фамилии на -швили и -дзе.
Возможно, что и "Пойя" относится к той же категории и не склоняются. В конце-концов, зачем всякий раз натягивать сову на глобус, пытаясь соблюсти далеко не очевидное правило )))

Glen5
06.09.2023 15:21Извините, а насчет Иваненко есть какое-то правило? Просто на мой русский слух вполне нормально сказать Иваненке, Иваненку.

wepp
06.09.2023 15:21+2Грамота.ру давным-давно сделала инструкцию по фамилиям (вам п.3).

eurol
06.09.2023 15:21А не пункт 7?

Dovgaluk
06.09.2023 15:21Пойя да, 7 пункт. Но вопрос в происхождении фамилии. Венгры пошли от финно-угров, поэтому не должно. Но Пойя из еврейской семьи, поэтому непонятно.

Aldrog
06.09.2023 15:21Но Пойя из еврейской семьи, поэтому непонятно.
Pólya в венгерском языке означает бинт, повязку, или (в геральдике) вертикальную полосу на щите. Так что происхождение фамилии особых вопросов не вызывает.
Другое дело, что пункт 7 говорит только о финских фамилиях, а не финно-угорских, и то с замечаниями (Преимущественно не склоняются… хотя в ряде источников рекомендуется склонять и их).

forever_live
06.09.2023 15:21Вроде как пункт 7 однозначно говорит, что фамилии с безударным "я" на конце склоняются, разве нет?

Mnemonic0
06.09.2023 15:21Для русского языка есть следущее правило: Мужские и женские фамилии и личные имена, которые оканчиваются на -О, -Е, -Э, -И, -Ы, -У, -Ю (ударные или безударные), а также на -А перед еще одной гласной, не склоняются.
Но есть один момент, в случае, если фамилия иностранная и выполнено её склонение на иностранном языке, то перевод будет уже склонённой фамилии. Соответвенно - если вы пишете статью на русском - то не склоняете, а если переводите - то в соответствии с тем, как написано на иностранном языке.

vesper-bot
06.09.2023 15:21Откуда вы взяли это правило? Кстати по нему "Пойа" тоже склоняется.

Mnemonic0
06.09.2023 15:21+1http://gramota.ru/class/istiny/istiny_8_familii/
3. Сразу опишем несколько групп несклоняемых фамилий. В современном русском литературном языке не склоняются русские фамилии, оканчивающиеся на -ых, -их (типа Черных, Долгих), а также все фамилии, оканчивающиеся на гласные е, и, о, у, ы, э, ю.
Если фамилия оканчивается на согласный (кроме фамилий на -ых, -их, о которых говорилось выше), то здесь – и только здесь! – имеет значение пол носителя фамилии. Все мужские фамилии, оканчивающиеся на согласный, склоняются – это закон русской грамматики.
И да - Гипотеза не Пойя, а Пойи, именно потому, что фамилия человека Пойа, а не Пойя. https://ru.wikipedia.org/wiki/Пойа,_Дьёрдь

AndrChm
06.09.2023 15:21В 1975 году вышел перевод книжки Д.Пойа «Математика и правдоподобные рассуждения». В издательстве «Наука». Кстати, уже в том далёком году, ещё при советах, переводчики не склоняли фамилию автора. Прочитайте хотя бы предисловие редактора перевода к этой книге и всё станет ясно. Безусловно, из этой книги многое можно почерпнуть. Так что её вообще стоит почитать. Но вот обсуждение относительно того, надо ли склонять, следует закрыть.

victor_1212
06.09.2023 15:21> Так что её вообще стоит почитать
насколько знаю Pólya читал лекции в IAS (Princeton) примерно по этой тематике, которыми в частности интересовался Einstein, так что действительно обе книги стоит посмотреть

avost
06.09.2023 15:21+3спотыкался: неужели фамилия "Пойя" склоняется?
Тоже удивился, поскольку почему-то считал, что ударение в фамилии падает на последнюю гласную, но пока читал статью подумал, что если на первую, то есть известный художник с аналогичной по структуре фамилией - Франциско Гойя и его фамилию принято склонять. У Пойи, судя по вики, ударение как у Гойи, так, что, вроде, тут всё нормально.

Spaceoddity
06.09.2023 15:21+1В данном случае я бы посоветовал сравнить с куда более "медийной личностью" - Франсиско Гойей))
Да, склоняется. Но при условии ударения на первый слог (как уж там оно в действительности - без понятия).
Иноязычные фамилии, оканчивающиеся на безударный гласный -а/-я, склоняются: Петрарка – стихи Франческо Петрарки, Кундера – роман Милана Кундеры, Гойя – картины Гойи, Кафка – романы Кафки, Капабланка – игра Капабланки, Окуджава – песни Окуджавы.
UPD: Ну и раз уж вы завели речь про грамматику - подушню: неэстетично.

Spaceoddity
06.09.2023 15:21Ну и беглый гуглёж показал, что с очень высокой долей вероятности (произношение имён в не самых распространённых языках - та ещё неопределённость) - ударение действительно на первый слог.

Aldrog
06.09.2023 15:21+1Да никакой неоднозначности нет, в венгерском, как и в финском, ударение всегда на первый слог.

Spaceoddity
06.09.2023 15:21Если только родители субъекта были не из какого-то этноса со своими языковыми заморочками, или просто не проявили фантазию.

Aldrog
06.09.2023 15:21Если только родители субъекта были не из какого-то этноса со своими языковыми заморочками
Да, если для него/его семьи венгерский не был основным языком, то могут быть варианты, но такие вещи обычно пишут в биографиях на самом видном месте, к тому же тут оригинальная запись фамилии очевидно венгерскую орфографию использует (и более того - совпадает с венгерским словом).
или просто не проявили фантазию.
А это уже что-то из разряда «у меня фамилия Иванов, но а читается как в английском top, а в как в yellow. Ни в коем случае не перепутайте!»

18741878
06.09.2023 15:21Эх, великая и могучая русская языка - каких только правил в нем нет! Хотя местами звучит странновато (чего стоят хотя бы варианты "многому научился читая Пойю" или "восхищаюсь Пойей").
P.S. Оба варианта (не эстетично или неэстетично) - допустимы. Трактовка, как обычно, довольно мутная, но однозначного правила - слитно или раздельно - я не нашел :) Плохо искал, вероятно?

Spaceoddity
06.09.2023 15:21Вероятно))
Можно заменить наречием без "не" - "уродливо", "коряво" и т.п. И одновременно с этим нет противопоставления: "не эстетично, а коряво".

piuzziconezz
06.09.2023 15:21+1Еще и имя Дьёрдь... Будто он был Джордж (или Георг, или просто Жора:) и у него были фефекты йечи.

Alexey2005
06.09.2023 15:21+5Что ж, по моим данным на этом диапазоне максимальное значение функции было равно
Просто представьте, как это было близко!Вот тут непонятно.
То есть всё это мозголомное опровержение через функции Римана оказалось чушью, и никакого контрпримера в указанном диапазоне не существует? Зато потом удалось найти контрпримеры на куда более мелких числах, нежели 8e360?
andreybrylb Автор
06.09.2023 15:21+3Существует, все нормально. Просто этот график Хазелгроув приводил как иллюстрацию к вычислениям + сказал "смотрите мы были близки к цели на небольших числах".
Но точность расчета у них была такая, что на этом промежутке они пропустили реальный максимум кумулятивной функции, который был равен "-2".

vladf
06.09.2023 15:21+2Из текста действительно не очевидно. После Вашего комментария и повторного просмотра статьи понял, что теоретически показали - есть переход через нуль значениях между 8E360-7Е367, а график построили всего-то для 44400-51600.
График под неравенством для L воспринимается как визуализация этого диапазона. И сразу возникает вопрос - "ну и где через ноль перешли?" :-)

Starl1ght
06.09.2023 15:21del

fasvik
06.09.2023 15:21Что? Не первый раз встречаю подобный комментарий (не только на Хабре), что он означает? Автор должен внезапно по вашему приказу удалить статью? Почему?

ksbes
06.09.2023 15:21+1Здесь нельзя удалять свои комментарии. Поэтому если написал что-то не то или не туда - комментарий редактируют и так помечают. Модераторы может даже потом их удаляют, если найдут.

sergio_nsk
06.09.2023 15:21+1Гипотеза Пойи утверждала, что чисел первого класса не меньше, как далеко бы мы не уходили на бесконечность.
Что-то я не понял, а где опровержение? Чисел первого класса на каком-то конечном отрезке стало меньше, но потом ведь после преодолении этого отрезка чисел первого класса снова стало больше.
https://habrastorage.org/r/w1560/getpro/habr/upload_files/480/f5f/155/480f5f1557af9a0594e38af1b53457c7.pngИсходя из формулировки гипотезы, опровержение - это когда начиная с какого-то числа, сумма L(x) всегда строго положительная.

Deosis
06.09.2023 15:21+3как далеко бы мы не уходили на бесконечность
Это как раз и значит, что чисел первого класса никогда не станет меньше

echo10
06.09.2023 15:21-3... "а в 1940 году некий индиец "досчитал" до 20 000) "
Древние кластера из индусов в действии!.....
Можно ли на них запустить DOOM?

victor-homyakov
06.09.2023 15:21+6— По приказу великого императора, включить компьютер! Приступить к встроенному тестированию!
Шеренга солдат, выстроившаяся посередине наклонной стены пирамиды, повторила команду при помощи флагов. В ту же секунду материнская плата из тридцати миллионов человек стала похожа на озеро, играющее яркими бликами в солнечный день. Взвивались и опускались миллионы флажков. На «дисплее», самом близком к пирамиде блоке, возникла и начала медленно удлиняться полоска зеленых флажков, показывающая прогресс тестирования в процентах. Через десять минут полоска дошла до конца.
— Встроенное тестирование окончено! Переходим к загрузке! Загрузить операционную систему!
По главной шине, проходящей через весь строй, полетела легкая кавалерия. Главная шина превратилась в бурную реку. Река разделилась на множество протоков, пронизывающих все модульные подразделения. Вскоре рябь черных и белых флажков слилась в единые волны, которые принялись перекатываться по всей материнской плате. Особенно бурлил центральный процессор — словно в него насыпали пороха и подожгли.
И вдруг движение в процессоре стало утихать и постепенно остановилось, словно порох вдруг выгорел. Затишье разошлось от процессора кругами по всем направлениям. Это было похоже на то, как замерзает море. Наконец вся материнская плата замерла, только несколько разрозненных элементов иногда безжизненно помаргивали, замкнувшись в бесконечном цикле. Центр дисплея замигал красным.
— Система зависла! — выкрикнул офицер-сигнальщик. Вскоре определили причину остановки: один из вентилей в регистре состояния процессора дал сбой.
— Перезагрузить систему! — уверенно скомандовал фон Нейман.
— Подождите! — Ньютон остановил офицера-сигнальщика и обратился к Цинь Шихуанди с коварной усмешкой на лице: — Ваше императорское величество, чтобы улучшить стабильность системы, надлежало бы принять корректировочные меры в отношении дефектных компонентов…
Цинь Шихуанди сжал свой меч и приказал:
— Заменить испортившийся компонент и отрубить головы всем его составляющим! На будущее запомните: при любом сбое будут приниматься те же меры!
Фон Нейман взглянул на Ньютона с отвращением. Несколько всадников с мечами наголо рванулись внутрь строя. После того, как засбоивший компонент «отремонтировали», была вновь дана команда перезагрузить систему. На этот раз операция прошла без сучка без задоринки. Двадцать минут спустя впервые в истории «Трех тел» живой человеческий компьютер, основанный на архитектуре фон Неймана, приступил к работе под управлением операционной системы Qin 1.0.
(c) Задача трёх тел

Vsevo10d
06.09.2023 15:21+5Кстати, это еще лайтовый эпизод, вот когда там частицу развернули в многомерном пространстве и лазерами с космических кораблей начали выжигать на ней микросхему, вот тогда я понял, что ничего до этого не знал о научной фантастике.

Seraphimt
06.09.2023 15:21+3Ещё в эту же тему: долгое время считалось, что функция Пи(х) - число простых чисел меньших х, всегда меньше интегрального логарифма, численно всё так и было вплоть до очень больших чисел. И тоже сперва теоретически доказали, что Пи(х) бесконечное число раз превосходит логарифм, а потом и нашли первое такое нарушение - оно не дальше, чем примерно 10^10^10^10^3, у этого числа даже есть своё название - число Скьюза. Потом эту оценку снижали постепенно, сейчас она имеет порядок 10^316

Wizard_of_light
06.09.2023 15:21Гомер Симпсон тоже может рассказать
про важность точных доказательств


Tyusha
06.09.2023 15:21+5Им стало число 906 180 359, а через 20 лет был найден наименьший на сегодняшний день показатель - 906 150 257
Не поняла? Приведённые числа это n в смысле L(n)? Или имеется в виду u в смысле L(e^u)? Смущает слово "показатель" в вашем тексте.

sebres
06.09.2023 15:21+1Приведённые числа это n в смысле L(n)?
Да.
Гипотеза не работает для большинства значенийnв районе906 150 257 ≤ n ≤ 906 488 079. В этой области суммирующая функция Лиувилля достигает максимального значения829приn = 906 316 571.(кстати 829 а не 849 как написано в статье).

saipr
06.09.2023 15:21-1я расскажу Вам очень показательную историю про одну математическую гипотезу из теории чисел. Она станет ярким примером того, как в математике прерываются, казалось бы, явные закономерности, и что любое предположение в этой науке нуждается в строгом доказательстве.
Отсюда следует, что только доказанные закономерности следует программировать и делать достоянием общества. В противном случае:
И тут случился шок! Хэш, подсчитанный «знаменитой реализацией Дегтярева» совпадал с хэшом, посчитанным в openssl с ГОСТ-ым endine, но не совпадал со значением хэш, посчитанным с помощью libgcrypt и libressl.
Здесь речь шла об open-source реализациях хэш-функции ГОСТ Р 34.11-2012.

mayorovp
06.09.2023 15:21+1А причём тут вообще математические закономерности, если там был косяк в реализации длинной арифметики?

wataru
06.09.2023 15:21+7Самый мощный пример, почему в метематике нельзя верить закономерностям - интегралы Борвейна:
И т.д: все интегралы дают одно и то же значние, пока синусов под знаком интеграла не станет восемь. Там вдруг значение интеграла станет меньше.
Вот статья и отличное видео от 3blue1brown с объяснениями.

agoncharov
06.09.2023 15:21+1Можно источник где верхний предел называют супремумом предела? По логике вещей это был бы не очень хороший термин, ведь он может конфликтовать с супремумом предела как от функции, который уж никак не то же самое, что и верхний предел

AndrChm
06.09.2023 15:21Для начала неплохо было бы выяснить, что Пойя не склоняется. Так что «Гипотеза Пойя». Прямо с заголовка начинается. Кое о чём говорит, конечно.

ksbes
06.09.2023 15:21Он - Пойа, так что склоняется.

AndrChm
06.09.2023 15:21Добрый день! Есть венгерский математик Дьёрдь Пойа. Склоняется ли его фамилия? В "Письмовнике" сказано, что фамилии на -а с предшествующим согласным не склоняются, если они французского происхождения. Фамилия Пойа выглядит вполне "по-французски", но он всё-таки венгр, поэтому закрались сомнения...
Ответ справочной службы русского языка
Фамилия Пойа в русском языке не склоняется

ksbes
06.09.2023 15:21+1А ссылку на правило не дали, как они обычно делают? А то этот ответ правилам прямо противоречит (см. обсуждение выше)
(да и ссылка на сам вопрос не помешала бы ...)

AndrChm
06.09.2023 15:21Метод был разработан известным математиком Д.Пойёй (Пойаем? Пойи? Пойаей? Пойай?). Попробуйте так написать. Никто эту корявость в жизни не примет просто потому, что не поймёт, о ком речь идёт. А вот ощущение безграмотности останется.
http://new.gramota.ru/spravka/buro/search-answer?s=фамилии на -а

Aldrog
06.09.2023 15:21Д.Пойёй (Пойаем? Пойи? Пойаей? Пойай?)
Откуда такие экзотические варианты? Разработан математиком Дьёрдем Пойей. Как минимум именительный падеж Пойа без проблем реконструируется из такой формы.
http://new.gramota.ru/spravka/buro/search-answer?s=фамилии на -а
Ответ никак не обоснован, в правилах на том же сайте написано ровно противоположное.
Но мне там нравится соседний ответ про китайские названия, где говорится, что склоняемость зависит от степени интеграции в язык. Вот это, пожалуй, неплохой аргумент за то, чтобы фамилию Пойа всё-таки не склонять.

x2v0
06.09.2023 15:21+5Эта статья - "один из самых ярких примеров того, что и в программировании «верить на слово» нельзя."
Автор привел в качестве примера неработающий код.
Я имею ввиду не только отсутствии табуляции, но и то, что даже после всех исправлений этот код выдаёт неправильный результат.
Например, для числа 293 из таблицы, результат должен быть -21.
Автор, пожалуйста, опубликуйте распечатку liouville_table.txt для этого числа.Вся статья - набор формул и картинок, в которых разобраться невозможно.
Автор "ради красного словца" пишет то, о чем, по-видимому, сам до конца не разобрался перепечатывая чужие слова, картинки.
Обсуждение - ничем не лучше.
Все кружится вокруг "КАК склоняется фамилия Пойя".
AndrChm
06.09.2023 15:21-1Вроде как это перевод, а не свой текст. Или же вольный пересказ оригинального английского текста. Такие вещи надо указывать. Что касается непонимания, частичного или полного, — так здесь это обычное дело. Ну, научился кое-что подвёрстывать в LaTeX, картинки вставлять. Надо себя потешить и другим показать, хотя правильно было бы дать ссылку на оригинал, а от себя написать внятный комментарий по существу. Но тут уже надо напрягаться.
Более того, открою страшную тайну, на зоне тоже на слово не верят. Особенно, если предъяву кинул. Обоснуй, скажут. Не сможешь — будешь спасаться как потный Микки Маус. Вот такая правда жизни.

NooneAtAll3
06.09.2023 15:21С использованием функции Лиувилля гипотеза переформулируется следующим образом:
Вы
\forall xзабылиПростейший код для вычисления на Python:
Как уже сказали другие, индентация слетела
Проблема была в том, что он рассмотрел не все возможные варианты.
Вы так выразились, как будто он их упустил и его поправляли. Это точно так?
Я бы перефразировал вПроблема была в том, что "большинство случаев" это не "все"находит не конструктивный пример,
Я споткнулся, когда читал… "не" с прилагательными итд-итп :/
Черточки обозначают минимальное и максимальное значение предела функции
В таком построении фразы как будто сам предел меняется.
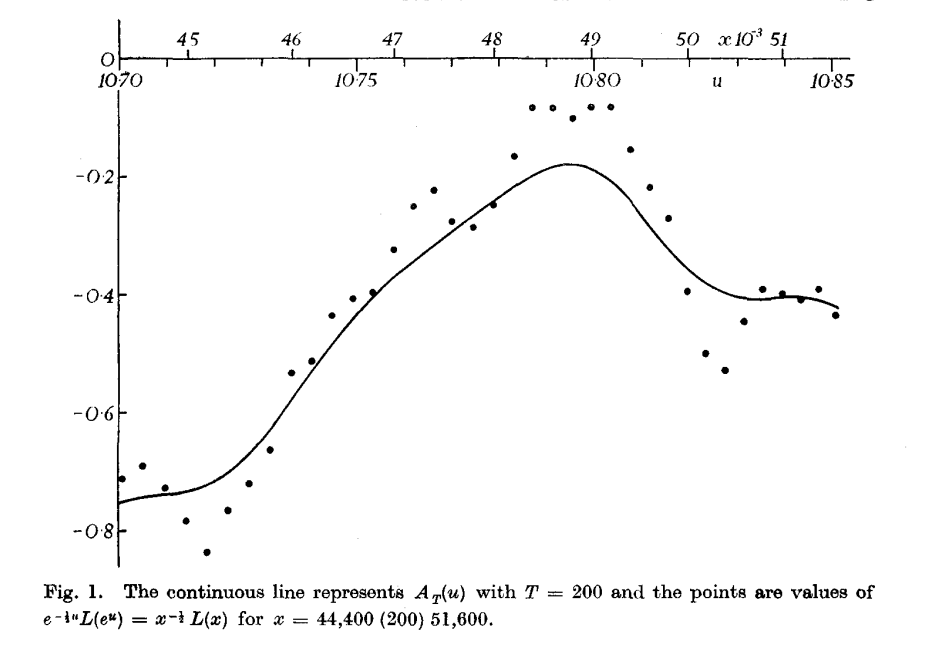
Нужные термины — "верхний" и "нижний" пределы (потому и чёрточки сверху и снизу, такое именно в советской математической летиратуре), а фразу для объяснения вывернуть шиворот-навыворот впредел минимальных и максимальных значенийА вот еще интересный момент: в оригинальной статье приводится график, где в ходе расчётов в диапазоне от 44 400 до 51 600 (шаг 200) удалось почти вплотную приблизиться к нулю. По графику видно, что значение равно примерно 70 — 80.
Что ж, по моим данным на этом диапазоне максимальное значение функции было равно:Нижнее предложение отвечает верхнему, а верхнее — подпись к картинке
Уже есть комментаторы что пропустили эту подпись и не понимают, как из примера про 10^360 вы перешли к 44 тысячам (и даже к тому что это 44 тысячи, а не вы на коленке проверили числа до 360 цифр). Описание картинок всегда надо делать самостоятельным, оно ж серое.И вообще лучше всего эту часть в спойлер упрятать — всё равно дополнение



3ycb
И эти люди запрещают нам
ковыряться в носмайнить биткоины. /sarcasmky0
Мы не запрещаем, а только намекаем, что триллионы — это при имеющихся мощностях курам на смех! :)
AlexanderS
Не запрещают, а возмущаются на трату кучи ресурсов с фактическим полезным выхлопом в виде теплового выхлопа. То ли дело научные работы… потом можно, например, научные статьи почитать… а что ваши битки?
piuzziconezz
Вот бы придумали криптовалюту, в процессе майнинга которой проверялась бы какая-нибудь математическая гипотеза. Тогда все было бы ради науки:)
Vsevo10d
Были Sia и еще кто-то, связанные с распределенными вычислениями, но я в свое время так и не смог настроить подключение к пулу по их мануалам и забил.
wataru
Нельзя, потому что это снижает цену атаки. Вся суть PoW — это сделать что-то абсолютно бесполезное, именно потратить ресурсы для доказательства хороших намерений.
Условно говоря, можно накраудфандить ботнет для решения очень важной и интересной математической гипотизы и заодно, не потратив почти ни цента, взломать сеть. Ну или потом филдсовской медалью отбить часть затрат на майнинг.
MikalaiR
Нет, необязательно это должно быть что-то бесполезное. Должен быть способ быстро и незатратно проверить что работа действительно выполнена, при этом сама работа должна быть затратной. Так что задачи вроде факторизации чисел сюда тоже подходят, да и многие другие "полезные", не только подбор хешей.
AndrChm
Не подходят. Факторизация на классическом компьютере возможна с субэкспоненциальной, а на квантовом с полиномиальной трудоёмкостью. Так же как и дискретная логарифмическая проблема. Существуют NP-полные задачи, вот они подходят. Не нужно делать подобных утверждений, если не специалист.
AlexanderS
В Folding Home пытались что-то этакое внедрить — начислялись коины в зависимости от длительности работы и набранных очков. Потом надо было разобраться как их забрать, перечислить на биржу, вывести в кеш, а сумма получалась не сильно мотивирующая… я даже разбираться не стал.
Fell-x27
PoS крипта держится на "заведомо решаемых" математических задачах, которые определяют порядок генерации блоков. Сами же ноды, в большинстве случаев, могут быть развернуты на обычных VPS. Никакого пустого расхода энергии на бесконечный перебор хэшей.
Если речь идёт о вычислении контрпримеров для какой-то гипотезы, то тут, если подойти серьёзно, две проблемы;
1) нелинейный рост сложности вычислений со временем. PoW крипта тоже наращивает сложность, но лишь в ответ на рост мощности сети, чтобы выдерживать матожидание блока на примерно одном уровне. Однако, в случае с гипотезами, сложность будет расти сама по себе.
2) Что делать с проектом, если гипотеза таки сломается? :) Скам экзит?
Вообще, есть какая-то монета, не помню название, которую выдают за вычисления для fold@home. Она напрямую не связана с проектом, это энтузиасты замутили для мотивации участников. Если рассуждать категориями полезности сжигания энергии, она то - что нужно.
Captain_in_the_Green_Hat
Хороший намек, как совершенно неожиданно вся экономика, завязанная на хитромудрую математику может накрыться медным тазом единовременно и утечь через вычислительную дырочку, оставленную специально или обнаруженную случайно