Сегодня я хочу рассказать Вам про известное утверждение из математического анализа, которое носит имя сразу трех знаменитых математиков 19 и 20 веков: Эмиля Бореля, Анри Лебега и Эдуарда Гейне.

Это утверждение иногда называют леммой, что как бы подчеркивая её "местечковость" и простоту доказательства, однако это совсем не так. Да, её разбирают уже на первом курсе на дисциплине "Математический анализ", но изначально за ней стоял огромный, тысячелетний опыт математического сообщества, а первые доказательства были не только частными, но и основывались на очень сложных теоретико-множественных конструкциях.

Однако, прежде чем перейти к самой теореме, нужно рассмотреть одно математическое понятие, которое является её основой. Итак, поехали!

Компакт

В первую очередь обговорим тот факт, что мы будем иметь дело с вещественной прямой со стандартной топологией, образованной интервалами, - т.е. тем объектом, который Вам знаком еще со школы.

Фраза "образованной интервалами" означает, что любое подмножество вещественной прямой мы можем некоторым образом составить из объединений или счетных пересечений открытых интервалов.

Возьмем для конкретики какой-нибудь открытый интервал Х. Мы всегда можем предъявить некоторое объединение открытых интервалов Y, которое будет содержать интервал Х.

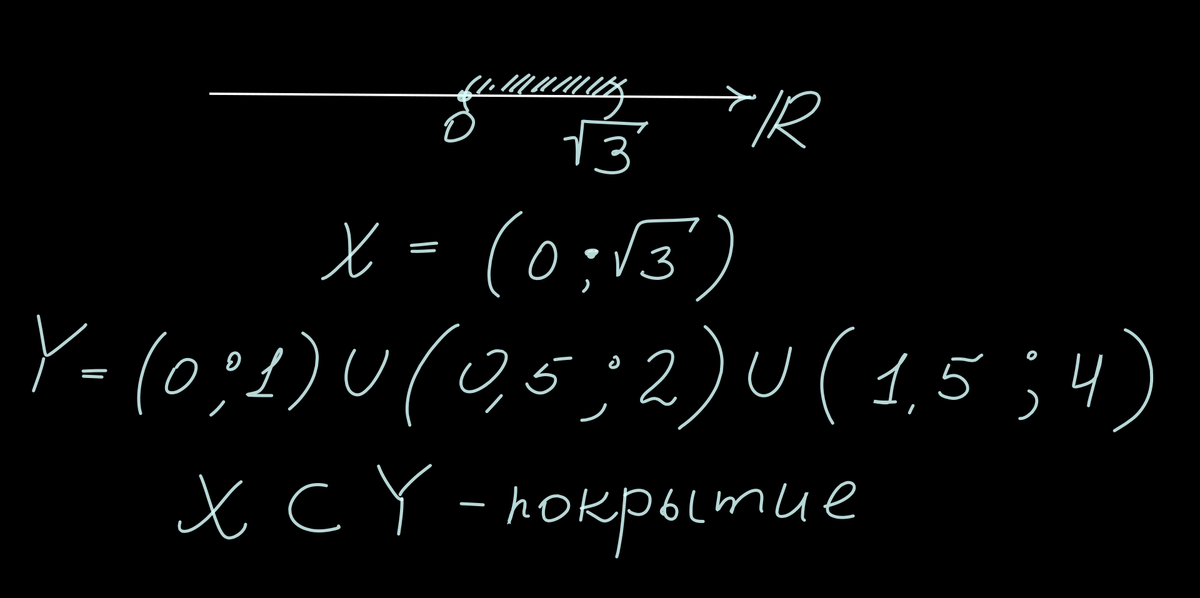
Таким образом, множество Y является покрытием множества Х. Заметим, что в покрытии Y мы можем выделить подмножество, которое будет называться подпокрытием:

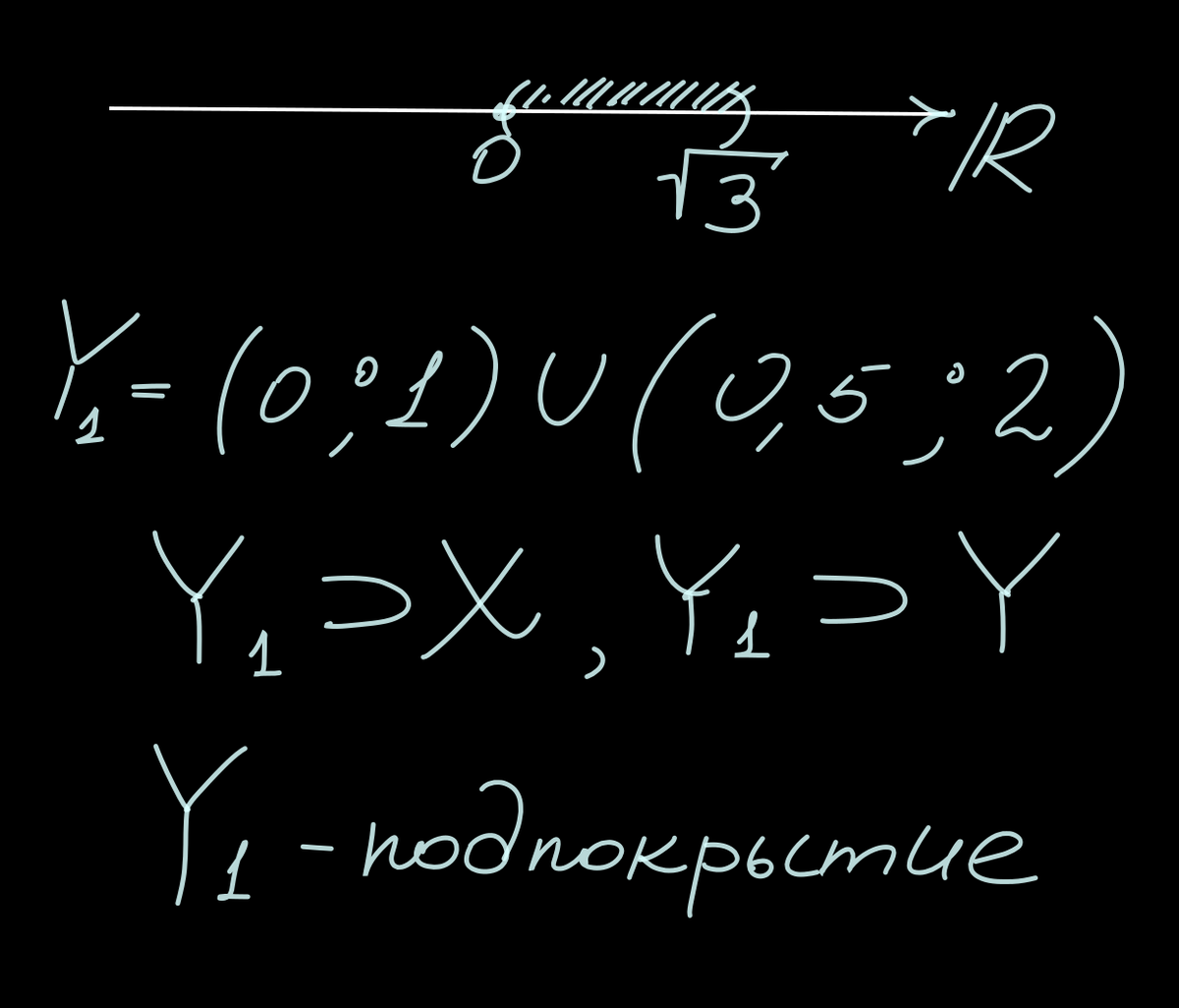
Обратите внимание, что мы смогли выбрать конечное подпокрытие из покрытия Y. Но всегда ли можно так сделать для имеющегося покрытия? Отнюдь!

Представим такое покрытие нашего интервала:

Можем ли мы выбрать из него конечное подпокрытие? Очевидно, что нет! Какое бы мы не взяли огромное число n для знаменателя интервала из покрытия, останется не покрытая часть интервала:

Итак, мы пришли к новому определению:

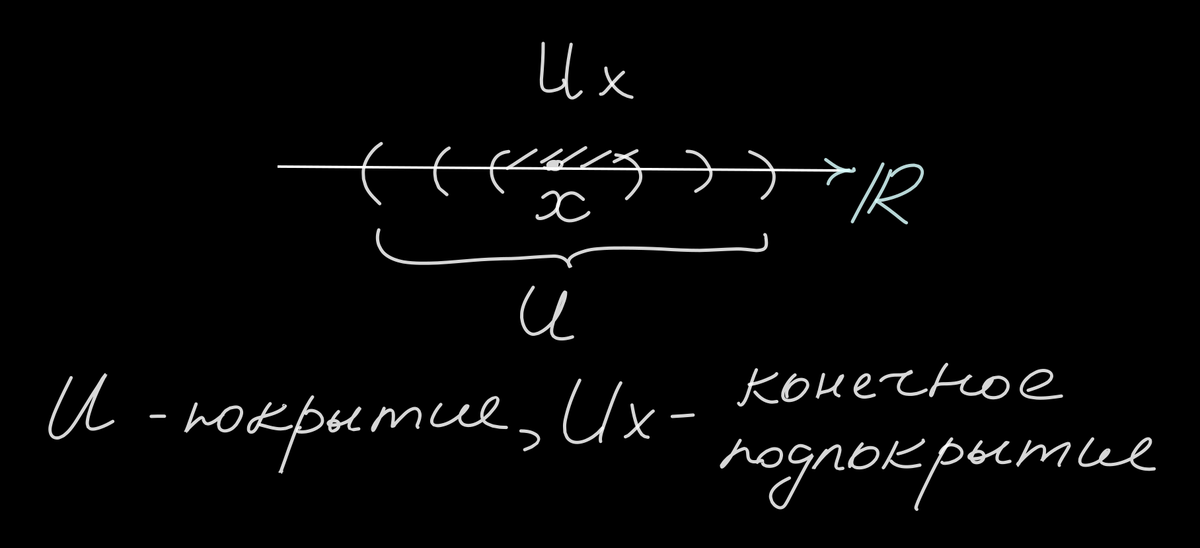
• Компактом называется такое множество, из каждого покрытия которого открытыми множествами можно выбрать конечное подпокрытие.

Очевидно, что интервал на вещественной прямой не является компактом. Интервал, конечно же, можно покрыть конечным числом открытых множеств (мы это как раз показали). Да и вообще всю прямую можно накрыть всего одним множеством - самой прямой, которая в стандартной топологии открыта.

Однако, говоря о компактности, мы подразумеваем, что из любого возможного, уже готового, покрытия множества, мы можем выбрать "ручками" конечное подпокрытие.

Самым простым компактом на прямой является, конечно, точка.

Но какова ситуация для отрезка? Именно этому и посвящена теорема Гейне-Бореля-Лебега.

Теорема Гейне-Бореля-Лебега

В одной из самых простых формулировок она гласит: "Отрезок - это компакт".

Как и большинство теорем, в которых нужно что-то показать для любого покрытия (множества, функции, пространства и т.д.), нужно использовать доказательство от противного. Здесь мы так же предположим, что из существующего покрытия отрезка нельзя выбрать конечное подпокрытие.

Тогда разделим отрезок на две части:

Тогда хотя бы одно из этих множеств (слева или (и) справа) не содержит конечного подпокрытия из того исходного, которое мы приняли сначала. Без потери общности предположим, что эта часть справа. Разделим её еще пополам, потом еще и еще и еще...

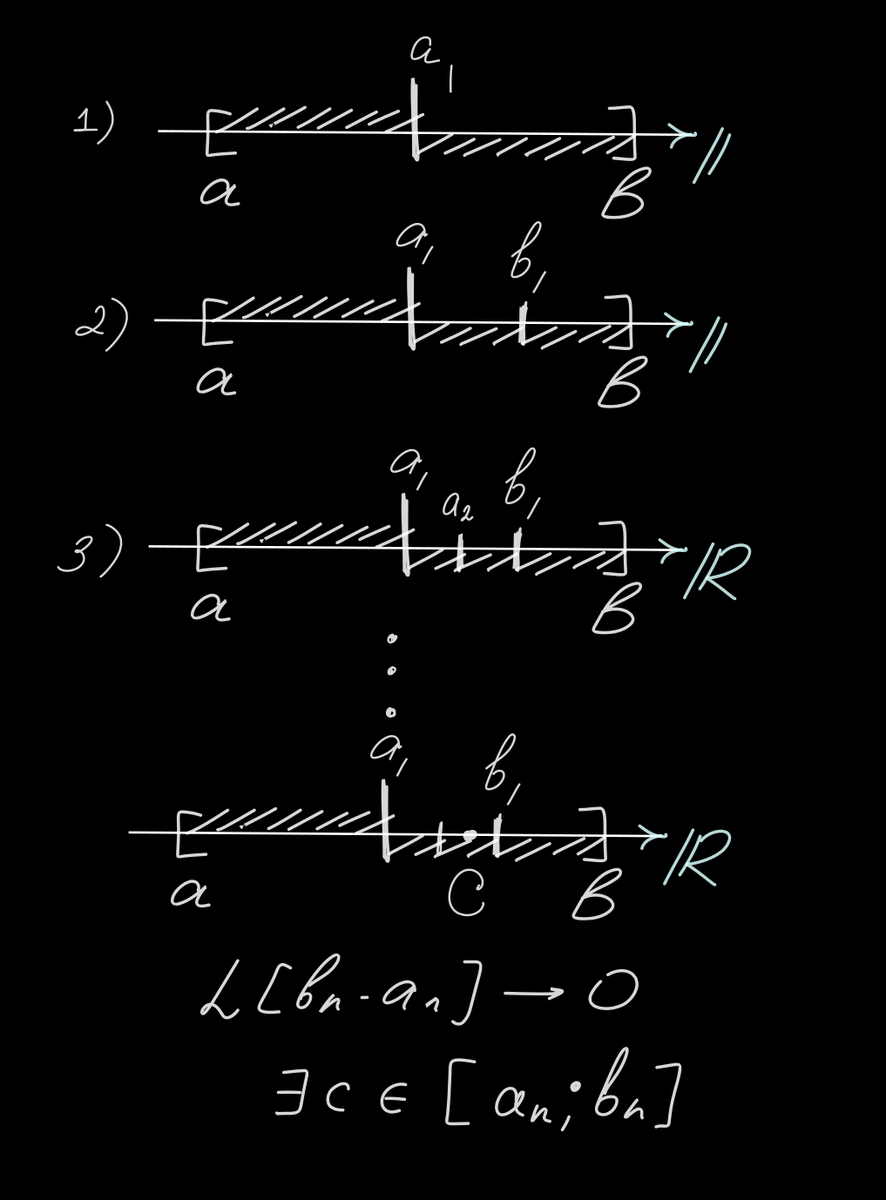
Значит существует такая точка c, которая является общей для всей этой последовательности вложенных отрезков (это утверждение - не менее фундаментальная лемма о вложенных отрезках).

Напоминаю, что мы каждый раз выбирали ту часть отрезка, у которой нет конечного подпокрытия. Теперь остановимся на точке с. Очевидно, что она входит в некоторый отрезок вместе со своей окрестностью:

Но мы можем продолжать увеличивать n! Рано или поздно мы получим, что в окрестность точки с залезет одна из половин либо целый отрезок, который, по предположению, не имеет конечного подпокрытия.

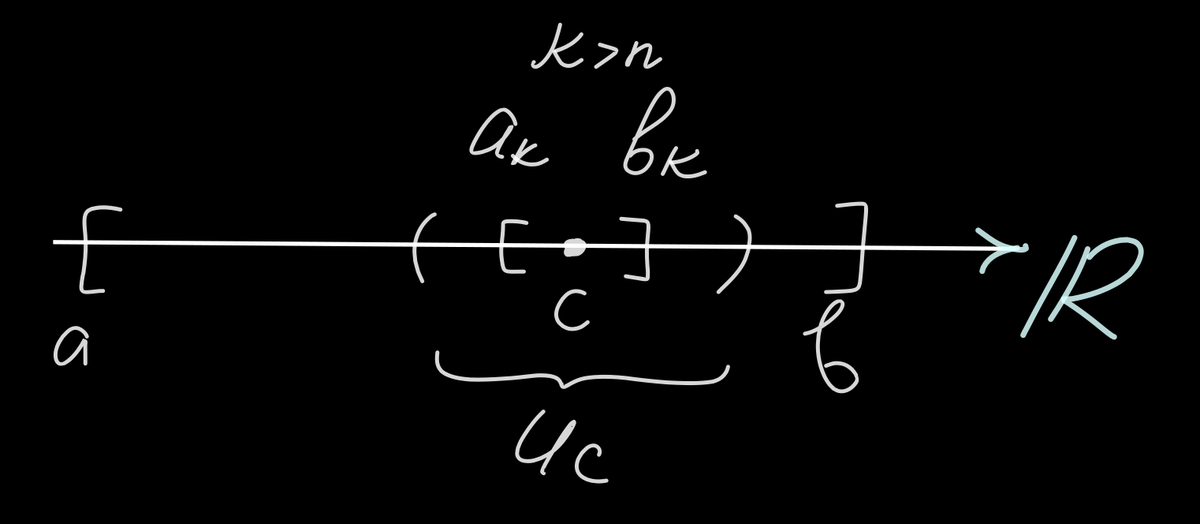
Но позвольте! Мы только что получили подпокрытие из одного открытого множества (Uc) для отрезка [Ak;Bk], который нельзя (опять-таки по предположению) покрыть конечным числом открытых множеств! Противоречие!

Значит, исходная посылка не верна, из системы покрывающих отрезок множеств всегда можно выбрать конечное подпокрытие, а, следовательно, по определению отрезок является компактом!

Теорема Гейне-Бореля-Лебега обобщается также и на стандартные пространства Rⁿ. Таким образом, теорему для прямой доказал Эдуард Гейне в 1872 году, теорему о том, что всякое счетное (бесконечное, но не континуальное) покрытие имеет конечное подпокрытие в Rⁿ доказал в 1895 году Эмиль Борель, а общий случай для несчетных покрытий - в 1904 году Анри Лебег. Именно поэтому, у этой "легкой" теоремы целых три великих отца.

• Больше математики в Telegram - "Математика не для всех".