Сегодня я хочу рассказать об удивительном геометрическом объекте, впервые рассмотренным советским математиком Игорем Федоровичем Шарыгиным.

Для начала посмотрите на рисунок ниже. Что Вы на нём видите?

Объясняю: слева заштрихован треугольник, вершины которого образованы основаниями медиан (делят сторону пополам), а справа - основаниями высот. Если большие треугольники не являются равнобедренными, то и заштрихованные равнобедренными быть не могут, это доказанный факт.
Но, погодите, есть же еще биссектрисы!
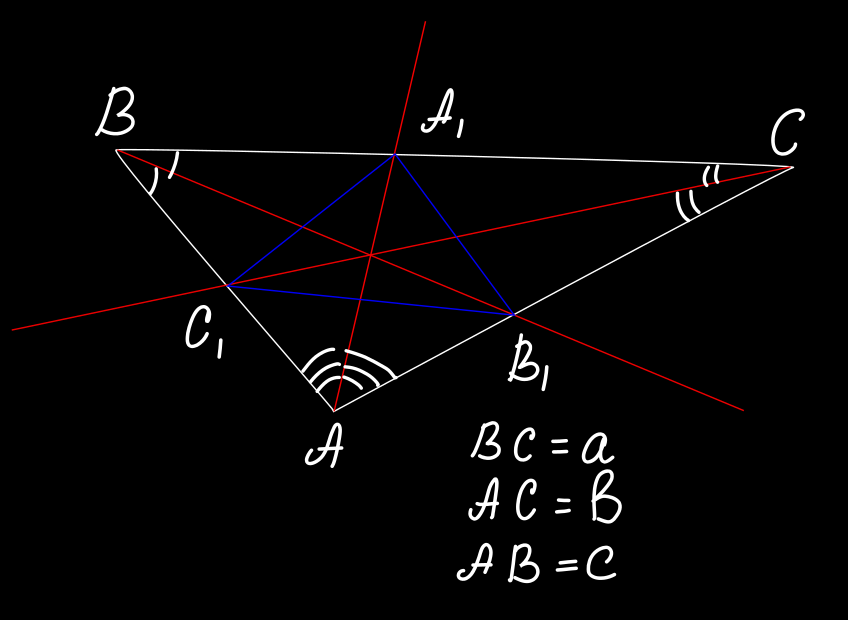
И тут становится интересно! Оказывается, и это показал Игорь Федорович, полученный из биссектрис треугольник может быть равнобедренным! Более того, есть одно очень тонкое условие: угол такого треугольника должен попадать в диапазон от 102,663 до 104,478 градусов!
Откуда такие странные цифры?
Дальнейшие разборки - дело для настоящих ценителей вкуса. Итак, мы предположим, что треугольник, показанный синим цветом на рисунке выше, является равнобедренным. Геометрическая часть доказательства сводится к поиску подобных треугольников и в итоге приводит к следующему выражению:

Затем это выражение раскрывается, а в пару к нему записывается теорема косинусов для большого треугольника:

Начинаем страдать! Нам нужно понять, что за условия накладываются на переменную х. Заметим абсолютную симметричность левой части выражения (9 слагаемых, полученных перемножением друг друга + 1 произведение сторон) и путём подбора получим:
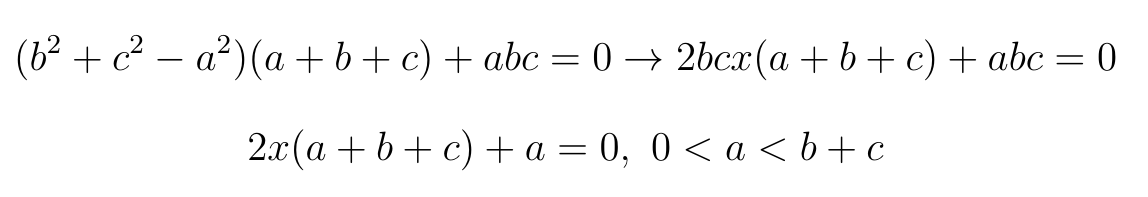
Теперь решаем уравнение и неравенство совместно:

Получили первое условие. Не пугайтесь, ведь x - в нашем случае это косинус угла, поэтому всё нормально. Идём дальше. подставляем выражение для стороны a в теорему косинусов:

Получили квадратное уравнение относительно y. Необходимо проверить, когда оно имеет решение, причём положительные (ведь y - это отношение сторон треугольника). Разделим на (4x+1), вычислим дискриминант и получим итоговое выражение для косинуса угла х:
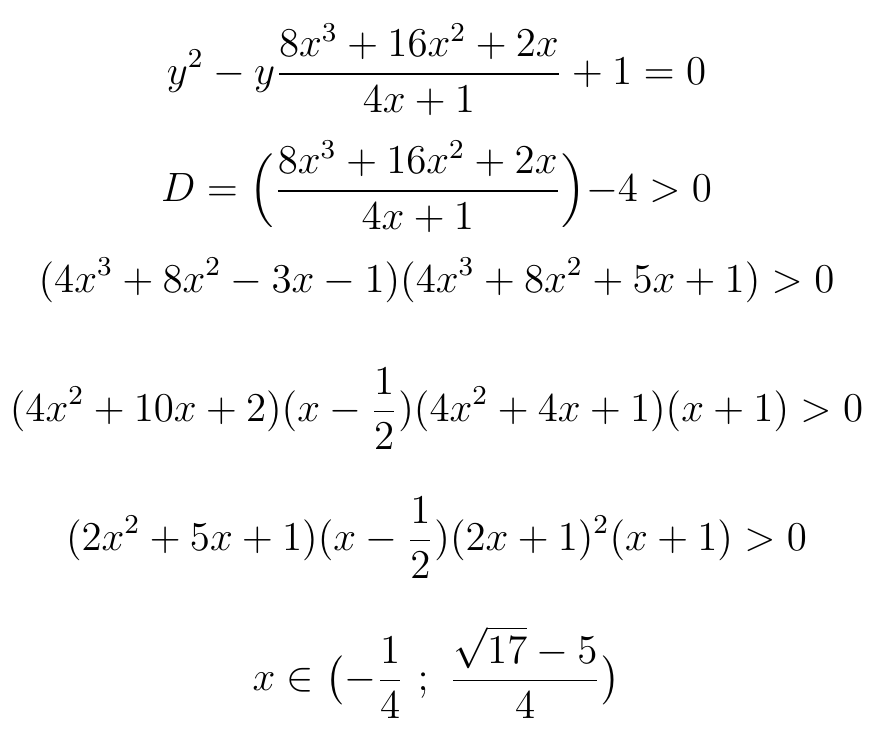
Итак, барабанная дробь! Мы получили, что косинус одного из углов треугольника Шарыгина должен быть больше минус 1/4 и меньше вот этого вот всего с радикалом. Вычисляем на калькуляторе:

А вот и реальные углы! Оцените полученный диапазон! Не знаю как Вы, но я испытал истинное наслаждение.
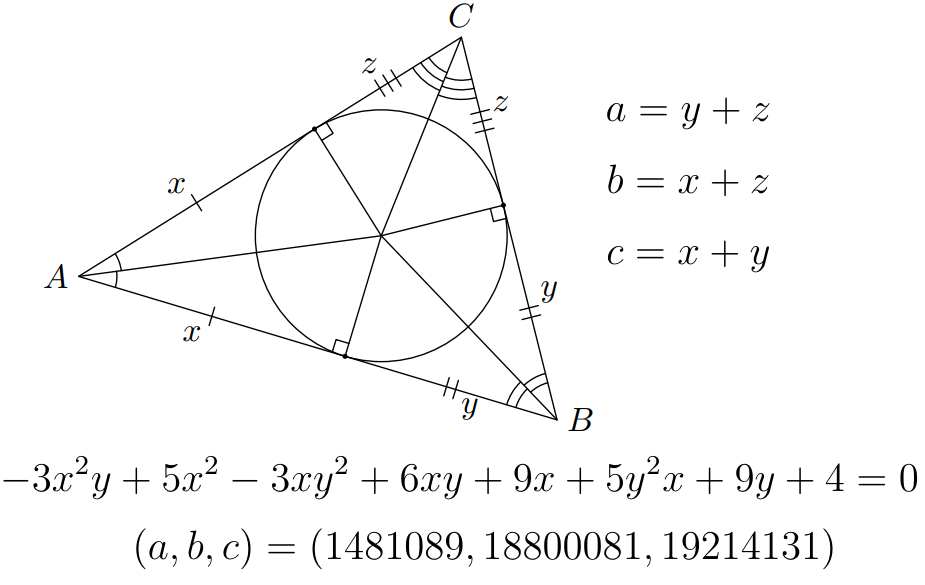
И еще один факт. Выше показан треугольник Шарыгина с наименьшими целочисленными сторонами. Красивый конец, неправда ли ?
Больше математики в Telegram - "Математика не для всех".
Эта статья поддерживается командой ITGLOBAL.COM
Мы — первый облачный провайдер в России, а также интегратор, поставщик ИТ-услуг, продуктов, сервисов и разработчик собственного ПО.
• Наш сайт
• Наш блог про Enterprise IT во всех его проявлениях
• Истории успеха наших клиентов
Комментарии (58)

kinall
19.09.2023 17:22+16Дежурный вопрос математику от не-математика:
Оказывается, и это показал Игорь Федорович, полученный из биссектрис треугольник может быть равнобедренным! Более того, есть одно очень тонкое условие: угол такого треугольника должен попадать в диапазон от 102,663 до 104,478 градусов!
- и что нам это даёт?

Porohovnik
19.09.2023 17:22+34Очень много, на самом деле.
Во-первых, алгоритм который будет работать с такими треугольниками, можно будет каким-то образом оптимизировать для вот таких вот углов.
Во-вторых нельзя сказать что все треугольники, образованные данным преобразованием, имеет неравнобедренные стороны, если исходный не равнобедренный
В-третьих это само по-себе интересно: особенные числа для Экливдовой геометрии, которые возможеы только в ней.

Indemsys
19.09.2023 17:22+14Если задача кажется надуманной и бессмысленной, то стоит поискать причины ее появления в связи с криптографией. Недаром тут длинные целые числа фигурируют.
В те времена был конкурс на поиск односторонних функций для криптографии. Таких чтобы очень трудно решить в прямом направлении, но очень легко проверить решение в обратном.
Может это отголоски той гонки.

Ktator
19.09.2023 17:22+49В фундаментальной науке, в отличие от прикладной, не стоит вопрос "зачем?".
Теория чисел 2000 лет не имела никакого практического применения, а потом вдруг пригодилась для криптографии.
Так что дежурный ответ: "мы (человечество) ещё немного продвинулись в математике".

Refridgerator
19.09.2023 17:22+4Той теории чисел, на которой построена криптография — намного меньше 2000 лет. Максимум пара сотен с натяжкой. Всё потому, что любая теория намного более эффективно развивается, как известны конечные цели и прикладные задачи. Даже всем известная теорема Ферма имела геометрический смысл, о котором даже в википедии почему-то не написано.
Что касается текущий статьи — то это не чистая математика, а геометрия. А у геометрии есть одно фундаментальное ограничение по определению — все построения делаются циркулем и линейкой, и этими же инструментами их решения и ограничиваются. Потому все задачи в геометрии так или иначе крутятся вокруг треугольников, а в решениях функции сложнее синусов и косинусов не фигурируют.

Sirion
19.09.2023 17:22+3> А у геометрии есть одно фундаментальное ограничение по определению — все построения делаются циркулем и линейкой, и этими же инструментами их решения и ограничиваются.
А можно определение в студию?
Refridgerator
19.09.2023 17:22Определение в самом слове "геометрия". "Гео" — земля, "метрия" — измерять. Измеряли тем, что доступно, а из доступного в те времена были только палка и верёвка.

ildarz
19.09.2023 17:22+11Со времен Евклида понятие геометрии немного изменилось и расширилось.

Refridgerator
19.09.2023 17:22+1Именно, что немного. То, что много — ушло в алгебру и смежные дисциплины — комплексные числа/кватернионы/матрицы/векторы/etc. Те же эллиптические кривые вы в курсе геометрии не обнаружите.

ildarz
19.09.2023 17:22+9
Открыл старый шкаф, достал первую попавшуюся книжку со словом "геометрия" в названии родом из 90-х, когда я ещё думал, что буду учёным, открыл на случайной странице оглавления.

Re1ter
19.09.2023 17:22+6с удовольствием посмотрю, как вы построите с помощью циркуля и линейки правильный семиугольник

Refridgerator
19.09.2023 17:22
Re1ter
19.09.2023 17:22Видимо, Вы не знакомы с теоремой Гаусса-Ванцеля.
В целом, следуя вашему определению, сама статья тоже не имеет отношения к геометрии, ведь невозможно построить треугольник по трём заданным биссектрисам, пользуясь только циркулем и линейкой.
Refridgerator
19.09.2023 17:22Конечно знаком, и именно об этом и шла речь — что ограничение «Теоре́ма Га́усса — Ванце́ля даёт необходимое и достаточное условие на то, что правильный n-угольник возможно построить с помощью циркуля и линейки» появилось не просто так. Ну а график в полярных координатах и абстрагирует циркуль, только с изменяемой длиной.

Re1ter
19.09.2023 17:22+2Используя поворотную линейку, тоже можно построить любой многоугольник, но ведь речь не об этом, верно? Речь о том, что определение геометрии никак не связано с какими-либо способами построения, коих можно придумать великое множество (расширяя инструменты, например, томагавком).
А как же стереометрия? Неевклидова геометрия? Или в вашем понимании геометрия это всего лишь раздел планиметрии, разрешимый в циркуле и линейке?
UPD: насчёт циркуля и линейки - всего лишь красивая обёртка для выразимых в радикалах чисел, не более.
Правильный n-многоугольник может быть построен циркулем и линейкой тогда и только тогда, когда при наличии на плоскости отрезка длины 1 можно построить отрезок, длина которого равна

— косинусу центрального угла данного n-многоугольника. Это, в свою очередь, верно тогда и только тогда, когда данный косинус является вещественно построимым числом, то есть может быть выражен при помощи целых чисел, простейших арифметических операций и извлечения квадратного корня.
UPD2: спасибо за кучу интересных статей из вашего профиля :)

Refridgerator
19.09.2023 17:22А как же стереометрия? Неевклидова геометрия?… Планиметрия?
Ну вот видите. Зачем изобретать новые слова и разделять между ними границы, когда уже есть «геометрия»? Наверное затем, чтобы ограничить спектр решаемых внутри них задач. Я бы ещё топологию вспомнил, которая тоже очевидно вышла из геометрии, но чуть подальше физической применимости.Или в вашем понимании геометрия это всего лишь раздел планиметрии, разрешимый в циркуле и линейке?
Если вас интересует моё понимание математики, то оно как раз и опирается на геометрию и физику в их историческом развитии.насчёт циркуля и линейки — всего лишь красивая обёртка для выразимых в радикалах чисел, не более
Сдаётся мне, что задача построения многоугольников появилось несколько раньше понятия радикала. Гаусс потому и смог её решить, что рассмотрел её с точки зрения алгебры, а не геометрии.

Re1ter
19.09.2023 17:22+1Так геометрия и есть общее понятие, включающее в себя всё вышеперечисленное, а никак не отдельная наука про циркули/линейки. Всё же стоит опираться на общепризнанные определения, а не изобретать свои, особенно для давно известных сущностей.
К слову, радикалы были известны ещё во II тысячелетии д.н.э. вавилонянам (как минимум, квадратные корни они извлекать умели), так что вопрос про радикалы и многоугольники остаётся открытым.

Re1ter
19.09.2023 17:22-4Когда заканчиваются аргументы, начинаются минусы в карму? С другой стороны, можете себе позволить, пуркуа бы и не па.

Refridgerator
19.09.2023 17:22+2С чего вы решили, что мне только плюсы в карму летят? Смысл копить карму в том и состоит, чтобы говорить то, что хочешь и так, как хочешь, а сводить любую дискуссию к карма-страданиям на хабре особо не приветствуется. Последнее слово и так за вами оставалось.

Kergan88
19.09.2023 17:22> Я бы ещё топологию вспомнил, которая тоже очевидно вышла из геометрии
Только из матана, а не из геометрии.

Portnov
19.09.2023 17:22+3Эллиптическими кривыми занимается раздел под названием алгебраическая геометрия. Внезапно :)
Я уж молчу про проективную геометрию, геометрию Лобачевского, Риманову геометрию, дифференциальную геометрию... К этим наукам уж совсем не представить, какое отношение имеют циркуль и линейка.

Sirion
19.09.2023 17:22+3Ну да. А потом кто-то захотел обменять своё круглое поле на равновеликое квадратное...

domix32
19.09.2023 17:22+2Той теории чисел, на которой построена криптография — намного меньше 2000 лет
Сомнительное утверждение. Модулярные числа использовали ещё во времена Месопотамии, то бишь ~6000 лет назад. Обобщённые теории понятное дело относительно недавнее событие, как впрочем и криптография как сущность, но они базируются на довольно древних концептах.
все построения делаются циркулем и линейкой
Это если речь за школьную планарную геометрию. Интегралы в общем-то тоже про геометрию. Как и более абстрактные варианты алгебраическиой геометрии. И многомерные пространства.

Refridgerator
19.09.2023 17:22+1Ну использовать это одно (часовой циферблат под модулярную арифметику тоже вполне подходит), а вот обосновать, посчитать и доказать вычислительную сложность — уже несколько другое. Эллиптические кривые тоже были известны задолго до, только вот применить их для доказательства теоремы Ферма получилось всего лишь 30 лет назад.

domix32
19.09.2023 17:22Шифр Цезаря тоже про модулярную арифметику и даже про криптографию. Это уже как минимум 50 лет сверху 2000.

Laryx
19.09.2023 17:22Насколько я помню, уже в античности широко использовался метод "вставки", или линейка с засечками - что позволяет строить и трисекцию угла, и удвоение куба, и ряд других задач, сводящихся к уравнениям третьей и четвёртой степеней (скажем, "Колодец Лотоса").

MegaMANGO
19.09.2023 17:22+51)После миллиарда задач где ответом являются 15х углы, подобный мелкий необычный диапазон в пару градусов просто эстетически приятен
2) математика фундаментальная наука, и даже если нет ни одной конкретной причины что-то исследовать, этим занимаются. Никогда не знаешь что и где пригодится на практике. Вдруг завтра откроют подраздел физики который будет использовать такие треугы, или откроется их полезное свойство в инженерии, например. Информация как их находить= минус головная боль.
3)Да и в принципе это интересно. Матеша интересна сама по себе, разве нет?

yatanai
19.09.2023 17:22Вспоминаю за теорию узлов где учёные просто на приколе решали странные задачки, которые неожиданно оказались сложными, а потом спустя столетие оказалось что не зря решали.

AVX
19.09.2023 17:22+36Итак, барабанная дробь!
несколько секунд думал, почему полученную дробь назвали "барабанной", а потом поржал над собой :)
В математике много такого интересного есть. Когда-то, лет 20 назад, изучал всякие такие штуковины, и неразгаданные задачи математики... после определённой наработки опыта в какой-то узкой области начинаешь уже подсознательно определять куда надо двигаться и что как можно вычислить, даже не зная теории, почему именно так. Порой считаешь что-то, а спустя пару месяцев находишь, что оказывается есть какая-то вот методика, и по ней всё чётко и понятно, а ты уже всё каким-то чутьём посчитал и что-то интересное откопал (правда, это оказывалось уже откопано давно, просто надо было интернет пошерстить, но тогда что-то не так много в нём было).

omaxx
19.09.2023 17:22+22не хотелось бы придираться, но этот треугольник точно не Шарыгина

т.к. он остроугольный... ну и соотношение сторон совсем не такое, как приведено ниже

Akela_wolf
19.09.2023 17:22+7Собственно до самого вкусного: "а как именно получены эти длины сторон? Существуют ли другие треугольники Шарыгина с целочисленными сторонами?" в статье не дошли. Такое ощущение что автор в чем-то разобрался, а то в чем не разобрался - отбросил и оборвал статью.

kknop
19.09.2023 17:22+11Вообще-то есть треугольник Шарыгина с прекрасными углами pi/7, 2pi/7, 4pi/7, - и в нем нужный факт (равнобедренность биссектрисного тр-ка) легко доказывается. Удивительно, как можно написать целую статью и не отметить в ней этот факт.

V2008n
19.09.2023 17:22+26И что самое интересное, в молекуле воды атомы водорода образуют именно такой угол.

Zara6502
19.09.2023 17:22+1всегда интересно (не в плохом смысле) как математику находят в окружающем мире не осознавая, что математика придумана как способ описания мира, поэтому было бы странно, если бы мы не находили математику вокруг нас. Но всегда интересно как на уровне молекул или простейших организмов работают простые числа, фракталы и т.п. Всегда создаётся ощущение магии.

idamdi
19.09.2023 17:22+6Прочитал сначала треугольник Шурыгиной

sneg2015
19.09.2023 17:22И смех, и грех







Tzimie
Я видел уже эту статью. Но поиском не нахожу
exTvr
Мнится мне, что это она и есть — издание второе, исправленное до неузнаваемости и дополненное.
andreybrylb Автор
Это действительно полная переработка моей старой статьй процентов на 95%
dlinyj
Возможно, просто эффект Манделы.
ainoneko
Ещё была статья не про это, а про "Is there a positive integer solution for a, b, and c if c/(a+b)+b/(a+c)+a/(b+c)=4":
Вот (там формула с первого взгляда похожа)