— Тони интересовался, — слабым голосом сказал Буш, — как согласуются, и согласуются ли вообще, божественное всемогущество и божественная всеблагость.
— И как ты ответил ему, о Джорджайя? — вопросил я.
— Я ответил… Я ответил, Господи, что из сложных словес ткут свою сеть фарисеи, а истина Духа обитает лишь в простоте. И в таком вопросе ее нет.

В. Пелевин, "Боги и механизмы"

Недавно мне задали вопрос "почему пересечение в TypeScript работает не как в теории множеств, а совсем наоборот?"

Озадачился, задумался и стал разбираться, как согласуются, и согласуются ли вообще операции "объединение" и "пересечение" в TypeScript и в теории множеств? И действительно ли пересечение в TypeScript работает прямо противоположно?

Вводные

1. В TypeScript есть операции "объединение" (Union, обозначается как I) и "пересечение" (Intersection, обозначается как &), предназначенные для создания нового типа на базе существующих, при этом:

   1. результат объединения расширяет область сущностей, удовлетворяющих новому типу,

   2. результат пересечения сужает область сущностей, удовлетворяющих новому типу

2. В теории множеств также есть операции "объединение" и "пересечение":

   1. Объединение - множество, содержащее в себе все элементы исходных множеств (иначе - расширенное множество):
      A = {1, 2}, B = {2, 3}, тогда A ∪ B = {1, 2, 3}

   2. Пересечение - это множество, которому принадлежат только элементы, которые одновременно принадлежат всем данным множествам (иначе - суженное множество):
      A = {1, 2}, B = {2, 3}, тогда A ∩ B = {2}

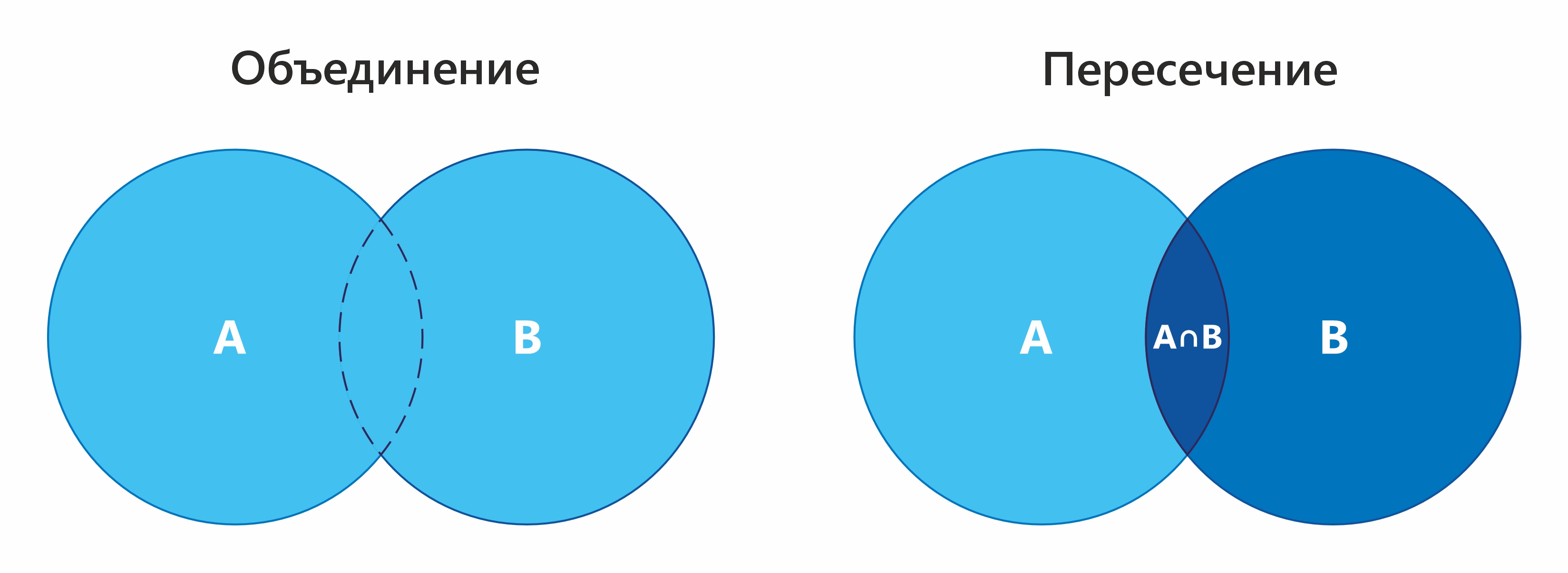
Успех с объединением

Операция "объединение" и там и там работает идентично, полученному на её основе типу удовлетворяют элементы, созданные на основе любого из исходных типов, либо элементы, реализующие все типы сразу.

Для примитивов:

type IPrimitiveSetA = 1 | 2;
type IPrimitiveSetB = 2 | 3;

type IUnionPrimitive = IPrimitiveSetA | IPrimitiveSetB; 

// любое значение одного из типов - ошибок нет
const unionPrimitiveOk1: IUnionPrimitive = 1;
const unionPrimitiveOk2: IUnionPrimitive = 2;
const unionPrimitiveOk3: IUnionPrimitive = 3;
// ошибка TS падает только если значения нет ни в одном исходном типе
const unionPrimitiveErr: IUnionPrimitive = 4;

Для объектов

type IObjectSetA = {
    a: number;
    b: number;
    isValid: boolean;
};
type IObjectSetB = {
    x: number;
    y: number;
    isValid: boolean;
};
type IUnionObject = IObjectSetA | IObjectSetB; 

// поля из обоих исходных типов - ошибок нет
const unionObjectAll: IUnionObject = {
    a: 1,
    b: 2,
    x: 3,
    y: 4,
    isValid: true
};
// поля только из типа А - ошибок нет
const unionObjectA: IUnionObject = {
    a: 1,
    b: 2,
    isValid: true
};
// поля только из типа B - ошибок нет
const unionObjectB: IUnionObject = {
    a: 1,
    b: 2,
    isValid: true
};
// всё из одного типа и часть из другого - ошибок нет
const unionObjectAB: IUnionObject = {
    a: 1,
    b: 2,
    x: 3,
    isValid: true
};
// ни один из типов не реализован полностью - ошибка
const unionObjectErr: IUnionObject = {
    a: 1,
    x: 3
};

Проблема с пересечением

Сначала посмотрим на числовые литералы. С ними все отлично, в результирующий тип попала только присутствующая в обоих наборах двойка. Всё как и при пересечении множеств.

type ISetLiteralA = 1 | 2;
type ISetPrimitiveB = 2 | 3;

type IIntersectionPrimitive = ISetPrimitiveA & ISetPrimitiveB; 

// падает ошибка, 1 не входит в пересечение (Type '1' is not assignable to type '2')
const intersectionPrimitive1: IIntersectionPrimitive = 1; 
// ошбики нет, 2 входит в оба множества
const intersectionPrimitive2: IIntersectionPrimitive = 2;

А теперь объекты.

Ориентируясь на теорию множеств легко подумать, что результатом пересечения будет тип, которому удовлетворяет объект, содержащий единственное общее для обоих типов поле isValid. Но поэкспериментировав и почитав руководство видим, что под новый тип подходит только объект содержащий все поля из всех исходных типов, то есть с точностью наоборот.

type ISetObjectA = {
    a: number;
    b: number;
    isValid: boolean;
};
type ISetObjectB = {
    x: number;
    y: number;
    isValid: boolean;
};

type IIntersectionObject = ISetObjectA & ISetObjectB;

// единственный корректный вариант
const intersectionObj:IIntersectionObject = {
    a: 1,
    b: 2,
    x: 3,
    y: 4,
    isValid: true
}

intersected Colorful and Circle to produce a new type that has all the members of Colorful and Circle - из официальной документации.

На цитате из документации можно успокоиться, сказать, что "множествам множественное, а тайпскрипту тайпскриптово". Но не может же быть одинаковое название операций простым совпадением?

Разбираемся с пересечением

Вспомним еще раз какую задачу решает операция пересечения:

1. сужает область допустимых значений, подходящих под результирующее множество,

2. обеспечивает, что элемент результирующего множества подойдет и к исходным множествам

Таким образом, если бы в нашем примере результирующим типом стал
type IIntersectionObject = { isValid: boolean; }, включающий только общее поле,
то объект, реализующий этот тип, не соответствовал бы ни одному из исходных типов ISetObjectA и ISetObjectB

При этом задача сужения типов также решена, так как количество возможных объектов типа IIntersectionObject несомненно меньше, чем количество объектов, удовлетворяющих типам ISetObjectA и ISetObjectB. Таким образом наличие всех полей в результирующем типе вполне логично.

Фокус в том, что о результирующем типе надо думать не как о суженном множестве полей объекта, а как о суженном множестве возможных объектов, удовлетворяющих типу.

Победа? Не совсем... Когда мы рассматривали пример с примитивами, число 2 подходило и под первый, и под второй исходный тип. А вот объект типа IIntersectionObject ни под один исходный тип не подходит, есть лишние поля. Как быть с этим?

Проверка избыточных свойств в TS

Рассмотрим пример:

type FnObjArg = { n: number };

const fn = (data: FnObjArg): number => {
    return data.n;
}
const arg = {n: 1, m: 2} as const;

// передаем в функцию объект - всё хорошо
const res1 = fn(arg);
// передаем тот же объект, создав его на месте, 
// и падает ошибка TS: 'm' does not exist in type 'FnObjArg'
const res2 = fn( { n: 1, m: 2} );

Это происходит благодаря такой особенности TS, как Excess Property Checks. В двух словах - это возможность указать для объекта больше свойств, чем есть в типе, главное при этом - передать необходимые свойства. Ошибка упадет только в следующих случаях:

type FnObjArg = { n: number, m: number };

const fn = (data: FnObjArg): number =>  data.n + data.m;

// при создании несоответствующего типу объекта при явном указании типа
// Object literal may only specify known properties, and 'p' does not exist in type 'FnObjArg'
const arg1:FnObjArg = {n: 1, p: 2};

// при передаче в функцию с типизированным аргументом объекта, в котором нет обязательных полей
const arg2 = {n: 1};
// Property 'm' is missing in type '{ n: number; }' but required in type 'FnObjArg'
fn(arg2);

Таким образом объект, соответствующий нашему результирующему типу, подойдет и исходным типам, т.к. TS "закрывает глаза" на лишние поля, лишь бы были обязательные.

Заключение

Итак, операция "пересечение" из теории множеств вполне согласуются с TypeScript, в чем мы достаточно подробно разобрались. Данной темы мельком касается замечательная статья "Понять TypeScript c помощью теории множеств" (глава "Интерфейсы и типы объектов"), в англоязычном stackoverflow есть открытые вопросы по теме "почему пересечение в TS работает противоположно теории множеств". Да и некоторых весьма опытных коллег вопрос поначалу ввёл в ступор, так что интерес к теме есть.

P.S. операции Union и Intersection идеально укладываются в дизъюнкцию и конъюнкцию соответственно, но это уже другая история.