К-ближайших соседей (K-Nearest Neighbors или просто KNN) — алгоритм классификации и регрессии, основанный на гипотезе компактности, которая предполагает, что расположенные близко друг к другу объекты в пространстве признаков имеют схожие значения целевой переменной или принадлежат к одному классу.

Ноутбук с данными алгоритмами можно загрузить на Kaggle (eng) и GitHub (rus).

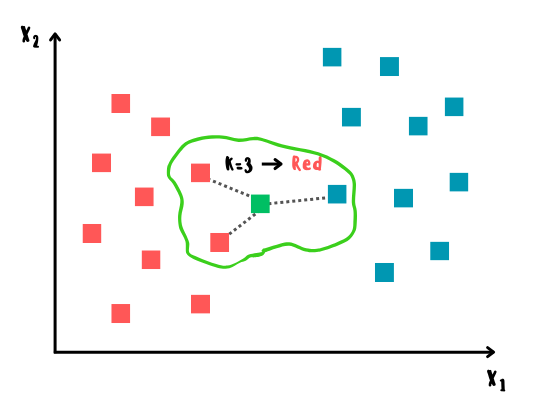
Принцип работы KNN

Алгоритм строится следующим образом:

• 1) сначала вычисляется расстояние между тестовым и всеми обучающими образцами;

• 2) далее из них выбирается k-ближайших образцов (соседей), где число k задаётся заранее;

• 3) итоговым прогнозом среди выбранных k-ближайших образцов будет мода в случае классификации и среднее арифметическое в случае регрессии;

• 4) предыдущие шаги повторяются для всех тестовых образцов.

Существует множество метрик для вычисления расстояния между объектами, среди которых наиболее популярными являются следующие:

• Евклидово расстояние — это наиболее простая и общепринятая метрика, которая определяется как длина отрезка между двумя объектами  и  в пространстве с признаками и вычисляется по формуле:

• Манхэттенское расстояние — метрика, которая определяется как сумма модулей разностей координат двух точек в пространстве между двумя объектами  и  с признаками и вычисляется по формуле:

• Косинусное расстояние — метрика, которая определяется как угол между двумя векторами  и  в пространстве с  признаками и вычисляется по формуле:

Более быстрые оптимизации

Описанный выше тип KNN называется Brute-Force, поскольку в нём используется метод полного перебора для поиска ближайших соседей, что делает его простым в реализации, но слишком медленным при работе с большим объемом данных. Для решения данной проблемы в реализации scikit-learn предусмотрены более продвинутые методы, основанные на бинарных деревьях, что позволяет получить значительный прирост в производительности.

BallTree

BallTree — это древовидная структура, в основе которой лежит разбиение исходного пространства данных на вложенные гиперсферы, что позволяет более эффективно отсекать большие области пространства, в которых отсутствуют ближайшие соседи для точек. В большинстве случаев такой алгоритм подходит для данных с произвольной метрикой расстояния.

Построение BallTree состоит из следующих шагов:

• 1) из множества точек выбирается одна случайным образом и для неё находится самая дальняя точка;

• 2) далее все точки разбиваются на сферы (узлы) по ближайшему расположению к двум точкам из шага 1, а расстояние между двумя сферами A и B в метрике M будет определяться следующим образом:

где и — центры сфер, а и — их радиусы.

• 3) затем данный процесс повторяется рекурсивно для каждой сферы, пока в ней не останется определённое количество точек или не будет достигнута заданная глубина дерева.

При поиске k-ближайших соседей для новой точки, алгоритм сравнивает расстояние от заданной точки до центра каждого дочернего узла и оставляет лишь те, в которых данное расстояние меньше радиуса узлов.

KD-Tree

KD-Tree (k-dimensional tree) — ещё одна древовидная структура, отдалённо напоминающая BallTree, однако в данном случае используются гиперплоскости для разбиения точек вместо гиперсфер, что позволяет также эффективно оставлять лишь те области пространства данных, в которых могут присутствовать ближайшие соседи. Обычно KD-Tree больше подходит для данных с евклидовой или манхэттенской метрикой расстояния.

Построение KD-Tree состоит из следующих шагов:

• 1) из множества точек выбирается одна из координат (обычно поочередно для каждого уровня дерева, но можно и случайным образом) и по ней вычисляется медиана;

• 2) далее все точки разбиваются на два узла (подмножества) по отношению к медиане: на те, у которых значение выбранной координаты меньше либо равно медиане, и на те, у которых больше;

• 3) данный процесс повторяется рекурсивно для каждого узла, пока в нём не останется определённое количество точек или не будет достигнута заданная глубина дерева.

При поиске ближайших соседей для новой точки, алгоритм сравнивает значение заданной точки с медианой в каждом узле, выбирая таким образом ближайшее подпространство, которое будет листом с ближайшими соседями. Возвращаясь обратно к корню, алгоритм будет сравнивать точки в текущем узле с ближайшими соседями и обновлять их значения в случае нахождения более близких к заданной точке.

Стоит также добавить, что KNN может применяться в контексте обучения без учителя, например в задачах кластеризации для вычисления расстояний между признаками, как в алгоритме DBSCAN (подробно можно ознакомится здесь). Для этого в scikit-learn существует специальный класс NearestNeighbors.

Импорт необходимых библиотек

import numpy as np
import matplotlib.pyplot as plt
from mlxtend.plotting import plot_decision_regions
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, r2_score
from sklearn.datasets import load_iris, load_diabetes
from sklearn.neighbors import KNeighborsClassifier, KNeighborsRegressor

Реализация на Python с нуля

class KNearestNeighbors:

    def __init__(self, n_neighbors=5, regression=False):
        self.n_neighbors = n_neighbors
        self.regression = regression

    def fit(self, X_train, y_train):
        self.X_train, self.y_train = X_train, y_train

    def _euclidean_distances(self, x_test_i):
        return np.sqrt(np.sum((self.X_train - x_test_i) ** 2, axis=1))

    def _make_prediction(self, x_test_i):
        distances = self._euclidean_distances(x_test_i)   # distances to all neighbors
        k_nearest_indexes = np.argsort(distances)[:self.n_neighbors]
        targets = self.y_train[k_nearest_indexes]   # k-nearest neighbors target values

        return np.mean(targets) if self.regression else np.bincount(targets).argmax()

    def predict(self, X_test):
        return np.array([self._make_prediction(x) for x in X_test])

Код для отрисовки графика

def decision_boundary_plot(X, y, X_train, y_train, clf, feature_indexes, title=None):
    feature1_name, feature2_name = X.columns[feature_indexes]
    X_feature_columns = X.values[:, feature_indexes]
    X_train_feature_columns = X_train[:, feature_indexes]
    clf.fit(X_train_feature_columns, y_train)

    plot_decision_regions(X=X_feature_columns, y=y.values, clf=clf)
    plt.xlabel(feature1_name)
    plt.ylabel(feature2_name)
    plt.title(title)

Загрузка датасетов

X1, y1 = load_iris(return_X_y=True, as_frame=True)
X1_train, X1_test, y1_train, y1_test = train_test_split(X1.values, y1.values, random_state=0)
print(X1, y1, sep='\n')


     sepal length (cm)  sepal width (cm)  petal length (cm)  petal width (cm)
0                  5.1               3.5                1.4               0.2
1                  4.9               3.0                1.4               0.2
2                  4.7               3.2                1.3               0.2
3                  4.6               3.1                1.5               0.2
4                  5.0               3.6                1.4               0.2
..                 ...               ...                ...               ...
145                6.7               3.0                5.2               2.3
146                6.3               2.5                5.0               1.9
147                6.5               3.0                5.2               2.0
148                6.2               3.4                5.4               2.3
149                5.9               3.0                5.1               1.8

[150 rows x 4 columns]
0      0
1      0
2      0
3      0
4      0
      ..
145    2
146    2
147    2
148    2
149    2
Name: target, Length: 150, dtype: int64

X2, y2 = load_diabetes(return_X_y=True, as_frame=True)
X2_train, X2_test, y2_train, y2_test = train_test_split(X2.values, y2.values, random_state=0)
print(X2, y2, sep='\n')


          age       sex       bmi        bp        s1        s2        s3  \
0    0.038076  0.050680  0.061696  0.021872 -0.044223 -0.034821 -0.043401   
1   -0.001882 -0.044642 -0.051474 -0.026328 -0.008449 -0.019163  0.074412   
2    0.085299  0.050680  0.044451 -0.005670 -0.045599 -0.034194 -0.032356   
3   -0.089063 -0.044642 -0.011595 -0.036656  0.012191  0.024991 -0.036038   
4    0.005383 -0.044642 -0.036385  0.021872  0.003935  0.015596  0.008142   
..        ...       ...       ...       ...       ...       ...       ...   
437  0.041708  0.050680  0.019662  0.059744 -0.005697 -0.002566 -0.028674   
438 -0.005515  0.050680 -0.015906 -0.067642  0.049341  0.079165 -0.028674   
439  0.041708  0.050680 -0.015906  0.017293 -0.037344 -0.013840 -0.024993   
440 -0.045472 -0.044642  0.039062  0.001215  0.016318  0.015283 -0.028674   
441 -0.045472 -0.044642 -0.073030 -0.081413  0.083740  0.027809  0.173816   

           s4        s5        s6  
0   -0.002592  0.019907 -0.017646  
1   -0.039493 -0.068332 -0.092204  
2   -0.002592  0.002861 -0.025930  
3    0.034309  0.022688 -0.009362  
4   -0.002592 -0.031988 -0.046641  
..        ...       ...       ...  
437 -0.002592  0.031193  0.007207  
438  0.034309 -0.018114  0.044485  
439 -0.011080 -0.046883  0.015491  
440  0.026560  0.044529 -0.025930  
441 -0.039493 -0.004222  0.003064  

[442 rows x 10 columns]
0      151.0
1       75.0
2      141.0
3      206.0
4      135.0
       ...  
437    178.0
438    104.0
439    132.0
440    220.0
441     57.0
Name: target, Length: 442, dtype: float64

Обучение моделей и оценка полученных результатов

KNN показал хороший результат в случае классификации. Также можно заметить, что алгоритм способен выстраивать нелинейные решающие границы, что позволяет ему также достигать хороших результатов с данными, в которых прослеживается нелинейная зависимость.

Однако, стоит обратить внимание на случай регрессии: низкий r2-score обусловлен небольшим числом ближайших соседей по умолчанию. Если увеличить число соседей до 30, то и r2-score увеличится более чем в 2 раза, что говорит о важности подбора оптимального числа ближайших соседей.

KNN classifier

knn_clf = KNearestNeighbors()
knn_clf.fit(X1_train, y1_train)
knn_clf_pred_res = knn_clf.predict(X1_test)
knn_clf_accuracy = accuracy_score(y1_test, knn_clf_pred_res)

print(f'KNN classifier accuracy: {knn_clf_accuracy:}')
print(knn_clf_pred_res)


KNN classifier accuracy: 0.9736842105263158
[2 1 0 2 0 2 0 1 1 1 2 1 1 1 1 0 1 1 0 0 2 1 0 0 2 0 0 1 1 0 2 1 0 2 2 1 0
 2]

KNN regressor

knn_reg = KNearestNeighbors(regression=True)
knn_reg.fit(X2_train, y2_train)
knn_reg_pred_res = knn_reg.predict(X2_test)
knn_reg_r2 = r2_score(y2_test, knn_reg_pred_res)

print(f'KNN regressor R2 score: {knn_reg_r2}')
print(knn_reg_pred_res)


KNN regressor R2 score: 0.18912404854026388
[253.6 188.6 183.2 138.4 177.8 189.6 111.8 229.  178.  266.8 147.6 193.8
 136.4  55.6 297.4  73.6  97.2  83.8 130.8 214.4 173.6 115.2 167.4 101.
 186.8 175.6  97.2  75.  172.4 144.2 205.4  63.8 161.6 190.8 110.2 159.2
 199.4 141.2 121.4 140.8 155.6 173.8 140.6 175.6 134.2  84.6 110.4 127.2
 107.4 209.2 130.2  78.2 183.6 105.  227.4 160.4 155.  104.6 119.2 175.8
 159.8 141.6 150.4 100.2 279.2 128.4  91.2 269.2 183.2  88.4 118.  151.6
  74.8  97.8 126.2 140.4 127.4 223.6 236.6 191.2 111.6 219.8  69.6 169.4
  87.6  92.6 112.  145.8 117.  153.2 115.2  92.8  67.6 172.   92.4 106.6
 208.4 173.8 113.2 104.4 141.6 128.2 226.   87.  247.6 147.6 223.6 217.2
 149.   72.6 182. ]

KNN classifier (scikit-learn)

sk_knn_clf = KNeighborsClassifier()
sk_knn_clf.fit(X1_train, y1_train)
sk_knn_clf_pred_res = sk_knn_clf.predict(X1_test)
sk_knn_clf_accuracy = accuracy_score(y1_test, sk_knn_clf_pred_res)

print(f'sk KNN classifier accuracy: {sk_knn_clf_accuracy:}')
print(sk_knn_clf_pred_res)

feature_indexes = [2, 3]
title1 = 'KNeighborsClassifier surface'
decision_boundary_plot(X1, y1, X1_train, y1_train, sk_knn_clf, feature_indexes, title1)


sk KNN classifier accuracy: 0.9736842105263158
[2 1 0 2 0 2 0 1 1 1 2 1 1 1 1 0 1 1 0 0 2 1 0 0 2 0 0 1 1 0 2 1 0 2 2 1 0
 2]

KNN regressor (scikit-learn)

sk_knn_reg = KNeighborsRegressor()
sk_knn_reg.fit(X2_train, y2_train)
sk_knn_reg_pred_res = sk_knn_reg.predict(X2_test)
sk_knn_reg_r2 = r2_score(y2_test, sk_knn_reg_pred_res)

print(f'sk KNN regressor R2 score: {sk_knn_reg_r2}')
print(sk_knn_reg_pred_res)


sk KNN regressor R2 score: 0.18912404854026388
[253.6 188.6 183.2 138.4 177.8 189.6 111.8 229.  178.  266.8 147.6 193.8
 136.4  55.6 297.4  73.6  97.2  83.8 130.8 214.4 173.6 115.2 167.4 101.
 186.8 175.6  97.2  75.  172.4 144.2 205.4  63.8 161.6 190.8 110.2 159.2
 199.4 141.2 121.4 140.8 155.6 173.8 140.6 175.6 134.2  84.6 110.4 127.2
 107.4 209.2 130.2  78.2 183.6 105.  227.4 160.4 155.  104.6 119.2 175.8
 159.8 141.6 150.4 100.2 279.2 128.4  91.2 269.2 183.2  88.4 118.  151.6
  74.8  97.8 126.2 140.4 127.4 223.6 236.6 191.2 111.6 219.8  69.6 169.4
  87.6  92.6 112.  145.8 117.  153.2 115.2  92.8  67.6 172.   92.4 106.6
 208.4 173.8 113.2 104.4 141.6 128.2 226.   87.  247.6 147.6 223.6 217.2
 149.   72.6 182. ]

Преимущества и недостатки KNN

Преимущества:

• простота в реализации и интерпретации;

• применяется во многих задачах, особенно в рекомендательных системах;

• высокая точность прогнозов при правильном подборе k и метрики расстояния.

Недостатки:

• большое потребление памяти и низкая скорость работы из-за хранения и вычисления расстояний между всеми обучающими и тестовыми образцами (имеется в виду KNN в чистом виде);

• чувствительность к выбросам и шуму, а также к несбалансированным классам в данных;

• при большом количестве признаков может возникнуть проблема совпадения метрической и смысловой близости объектов, что решается с помощью обучения представлений (численное описание объектов).

Дополнительные источники

Статьи:

• «Brute-Force k-Nearest Neighbors Search on the GPU», Shengren Li and Nina Amenta;

• «Unsupervised Space Partitioning for Nearest Neighbor Search», Abrar Fahim, Mohammed Eunus Ali and Muhammad Aamir Cheema;

• «Ball-tree: Efficient spatial indexing for constrained nearest-neighbor search in metric spaces», Mohamad Dolatshah, Ali Hadian and Behrouz Minaei-Bidgoli;

• «Developments in KD Tree and KNN Searches», Vijay R. Tiwari.

Документация:

• описание KNN;

• KNeighborsClassifier;

• KNeighborsRegressor;

• NearestNeighbors.

Видео: один, два, три.

? Метод опорных векторов (SVM) | Дерево решений (CART) ?