Линейная регрессия. Основная идея, модификации и реализация с нуля на Python / forpes.ru

Главная
Линейная регрессия. Основная идея, модификации и реализация с нуля на Python

Линейная регрессия. Основная идея, модификации и реализация с нуля на Python

30.03.2024 19:20

egaoharu_kensei 11 7100 Источник

В машинном и глубоком обучении линейная регрессия занимает особое место, являясь не просто статистическим инструментом, но а также фундаментальным компонентом для многих более сложных концепций. В данной статье рассмотрен не только принцип работы линейной регрессии с реализацией с нуля на Python, но а также описаны её модификации и проведён небольшой сравнительный анализ основных методов регуляризации. Помимо этого, в конце указаны дополнительные источники для более глубокого ознакомления.

Ноутбук с данными алгоритмами можно загрузить на Kaggle (eng) и GitHub (rus).

Содержание

Определение линейной регрессии
Полиномиальная регрессия
Регуляризация линейной регрессии (Ridge, Lasso, ElasticNet)
Преимущества и недостатки линейной регрессии
Дополнительные источники

Определение линейной регрессии

Линейная регрессия (Linear regression) — один из простейший алгоритмов машинного обучения, описывающий зависимость целевой переменной от признака в виде линейной функции . В данном случае была представлена простая или парная линейная регрессия, а уравнение вида $f_{w, b}(x) = w_0x_0 + w_1x_1 +... + w_{n}x_{n} + b = w \cdot x + b$ называется множественной линейной регрессией, где — смещение модели, — вектор её весов, а — вектор признаков одного обучающего образца.

К другим условиям определения линейной регрессии относятся гомоскедастичность (дисперсия остатков постоянна и конечна), а также отсутствие мильтиколлинеарности (линейной зависимости между признаками).

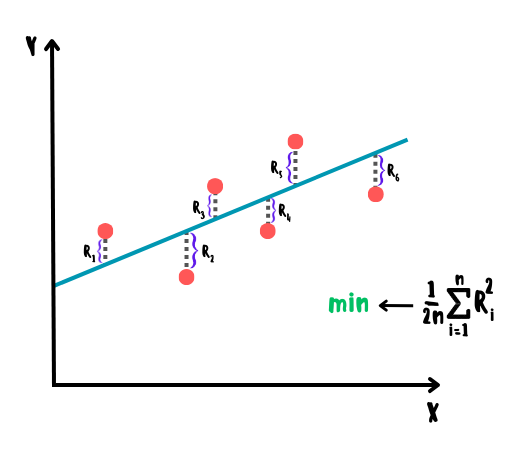
Метод наименьших квадратов и функция потерь

Выбор регрессионной линии (плоскости), описывающей взаимосвязь данных наилучшим образом, заключается в минимизации функции потерь , представленной в виде среднеквадратичной ошибки. Проще говоря, линия должна проходить через данные таким образом, чтобы в среднем разница квадратов ожидаемых и реальных значений была минимальна. Данный метод называется методом наименьших квадратов.

При наличии же большого количества выбросов в данных, более эффективным может оказаться метод наименьших модулей, однако у него есть один серьёзный недостаток: функция модуля не является дифференцируемой в точке , что в ряде случаев может затруднить минимизацию ошибки модели. Следовательно, исходя из теоремы Гаусса-Маркова, метод наименьших квадратов является наиболее оптимальной оценкой параметров модели среди всех линейных и несмещённых оценок за счёт меньшей дисперсии.

Вывод нормального уравнения (least squares normal equation)

$J(w, X, y) = \frac{1}{2n} \sum\limits_{i = 1}^{n} (w^T x_i - y_i)^2 = \frac{1}{2n} ||X w - y||^{2} = \frac{1}{2n} (X w - y)^T (X w - y) = \\ = \frac{1}{2n} ((X w)^T X w - (X w)^T y - y^T X w + y^T y) = |(X w)^T y = y^T X w| = \\ = \frac{1}{2n} (w^T X^T X w - 2 y^T X w + y^T y)$ $\frac{\partial J}{\partial w} = 0 \ \ \Rightarrow \ \ \frac{1}{2n} (2X^TX w - 2X^T y) = 0 \ \ \Rightarrow \ \ X^TX w = X^T y \ \ \Rightarrow \ \ \\ \Rightarrow w = (X^TX)^{-1} X^T y$

Принцип работы линейной регрессии

Существуют 2 основных способа обучения линейной регрессии:

1) Прямое (нормальное) уравнение в аналитической виде $w = (X^{T}X)^{-1}X^{T} y$ , где в данном случае — вектор весов, включая смещение . Главный недостаток данного способа заключается в высокой вычислительной сложности при большом количестве признаков.
2) Итеративная оптимизация с постепенным снижением ошибки модели на основе градиентного спуска и его разновидностей. Именно данный способ чаще всего используется на практике.

Линейная регрессия на основе градиентного спуска строится следующим образом:

1) изначально устанавливаются нулевые значения для весов, смещения и их градиентов;
2) на основе установленных значений делается прогноз;
3) на основе полученного прогноза пересчитываются значения весов и смещения, а также снижение их градиентов (разность значений на текущей и предыдущей итерациях);
4) шаги 2-3 повторяются до тех пор, пока снижение градиентов не станет меньше заранее установленного порогового значения;
5) итоговым прогнозом будет линейная комбинация полученных весов + смещение и признаков на тестовой выборке.

Формулы для расчётов

Градиенты смещения и весов:

$\begin{align} \frac{\partial J(\Theta)}{\partial b} &= \frac{1}{n} \sum\limits_{i = 1}^{n} (f_{w ,b}(x_i) - y_i) \\ \frac{\partial J(\Theta)}{\partial w} &= \frac{1}{n} \sum\limits_{i = 1}^{n} (f_{w ,b}(x_i) - y_i) x_i \\ \end{align}$

Правило обновления смещения и весов на основе градиентного спуска:

$\begin{align} \text{repeat}&\text{ until convergence:} \; \lbrace \newline\; & b_j = b_{j-1} - \alpha \frac{\partial J(\Theta)}{\partial b_j} \\ & w_j = w_{j-1} - \alpha \frac{\partial J(\Theta)}{\partial w_j} \newline \rbrace \end{align}$

Где:

$\alpha$ — скорость обучения;
— текущая итерация для смещения и весов;
$\Theta$ — матрица параметров.

Импорт необходимых библиотек

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import scale, PolynomialFeatures
from sklearn.linear_model import LinearRegression, Ridge, Lasso, ElasticNet
from sklearn.metrics import mean_absolute_percentage_error, mean_squared_error, r2_score

Реализация на Python с нуля

Линейная регрессия на основе матричного метода

class MatrixLinearRegression:

    def fit(self, X, y):
        X = np.insert(X, 0, 1, axis=1)   # add ones vector
        XT_X_inv = np.linalg.inv(X.T @ X)   # (X.T * X) ** (-1) inverse matrix
        weights = np.linalg.multi_dot([XT_X_inv, X.T, y])   # XT_X_inv * X.T * y
        self.bias, self.weights = weights[0], weights[1:]

    def predict(self, X_test):
        return X_test @ self.weights + self.bias

Линейная регрессия на основе пакетного градиентного спуска

class GDLinearRegression:
    def __init__(self, learning_rate=0.01, tolerance=1e-8):
        self.learning_rate = learning_rate
        self.tolerance = tolerance

    def fit(self, X, y):
        n_samples, n_features = X.shape
        self.bias, self.weights = 0, np.zeros(n_features)
        previous_db, previous_dw = 0, np.zeros(n_features)

        while True:
            y_pred = X @ self.weights + self.bias
            db = 1 / n_samples * np.sum(y_pred - y)
            dw = 1 / n_samples * X.T @ (y_pred - y)
            self.bias -= self.learning_rate * db
            self.weights -= self.learning_rate * dw

            abs_db_reduction = np.abs(db - previous_db)
            abs_dw_reduction = np.abs(dw - previous_dw)

            if abs_db_reduction < self.tolerance:
                if abs_dw_reduction.all() < self.tolerance:
                    break

            previous_db = db
            previous_dw = dw

    def predict(self, X_test):
        return X_test @ self.weights + self.bias

Загрузка датасета

Для обучения моделей будет использован Multiple Linear Regression Dataset, где необходимо спрогнозировать доход сотрудников на основе их возраста и опыта.

df_path = "/content/drive/MyDrive/income.csv"
income = pd.read_csv(df_path)
X1, y1 = income.iloc[:, :-1].values, income.iloc[:, -1].values
X1_scaled = scale(X1)
X1_train, X1_test, y1_train, y1_test = train_test_split(X1, y1, random_state=0)
X1_train_s, X1_test_s, y1_train, y1_test = train_test_split(X1_scaled, y1, random_state=0)
print(income)

correlation_matrix = income.corr()
correlation_matrix.style.background_gradient(cmap='coolwarm')


    age  experience  income
0    25           1   30450
1    30           3   35670
2    47           2   31580
3    32           5   40130
4    43          10   47830
5    51           7   41630
6    28           5   41340
7    33           4   37650
8    37           5   40250
9    39           8   45150
10   29           1   27840
11   47           9   46110
12   54           5   36720
13   51           4   34800
14   44          12   51300
15   41           6   38900
16   58          17   63600
17   23           1   30870
18   44           9   44190
19   37          10   48700

                age     experience    income
age          1.000000    0.615165    0.532204
experience   0.615165    1.000000    0.984227
income       0.532204    0.984227    1.000000

Обучение моделей и оценка полученных результатов

Как и ожидалось, линейная регрессия показала хорошие результаты в связи с линейной зависимостью в используемых данных. На графике также видно как полученная плоскость хорошо описывает линейную взаимосвязь в данных. Стоит также добавить, что в многомерном пространстве вместо линии или плоскости связь в данных будет описываться гиперплоскостью размерностью .

Linear regression (matrix method)

matrix_linear_regression = MatrixLinearRegression()
matrix_linear_regression.fit(X1_train_s, y1_train)
matrix_lr_pred_res = matrix_linear_regression.predict(X1_test_s)
matrix_lr_r2 = r2_score(y1_test, matrix_lr_pred_res)
matrix_lr_mape = mean_absolute_percentage_error(y1_test, matrix_lr_pred_res)

print(f'Matrix Linear regression  R2 score: {matrix_lr_r2}')
print(f'Matrix Linear regression MAPE: {matrix_lr_mape}', '\n')

print(f'weights: {matrix_linear_regression.bias, *matrix_linear_regression.weights}')
print(f'prediction: {matrix_lr_pred_res}')


Matrix Linear regression  R2 score: 0.9307237996010834
Matrix Linear regression MAPE: 0.04666577176525877 

weights: (40922.38666080836, -1049.7866043343445, 8718.76435636617)
prediction: [46528.00800666 35018.47848628 49448.73803373 38604.36954966
 30788.13913983]

Linear regression

linear_regression = GDLinearRegression()
linear_regression.fit(X1_train_s, y1_train)
pred_res = linear_regression.predict(X1_test_s)
r2 = r2_score(y1_test, pred_res)
mape = mean_absolute_percentage_error(y1_test, pred_res)

print(f'Linear regression R2 score: {r2}')
print(f'Linear regression MAPE: {mape}', '\n')

print(f'weights: {linear_regression.bias, *linear_regression.weights}')
print(f'prediction: {pred_res}')


Linear regression R2 score: 0.9307237996010985
Linear regression MAPE: 0.04666577176525461 

weights: (40922.386660807955, -1049.7866043338142, 8718.76435636563)
prediction: [46528.00800666 35018.47848628 49448.73803373 38604.36954966
 30788.13913983]

Linear regression (scikit-learn)

Как можно было заметить, в данном случае получились другие веса так как в предыдущих случаях модели обучались на масштабированных признаках. Если текущую модель обучить на масштабированных признаках, то веса будут такие же как и в случаях выше.

sk_linear_regression = LinearRegression()
sk_linear_regression.fit(X1_train, y1_train)

sk_lr_pred_res = sk_linear_regression.predict(X1_test)
sk_lr_r2 = r2_score(y1_test, sk_lr_pred_res)
sk_lr_mape = mean_absolute_percentage_error(y1_test, sk_lr_pred_res)

print(f'Scikit-learn Linear regression R2 score: {sk_lr_r2}')
print(f'Scikit-learn Linear regression MAPE: {sk_lr_mape}', '\n')

print(f'weights: {sk_linear_regression.intercept_, *sk_linear_regression.coef_}')
print(f'prediction: {sk_lr_pred_res}', '\n')

sk_linear_regression.fit(X1_train_s, y1_train)
print(f'scaled weights: {sk_linear_regression.intercept_, *sk_linear_regression.coef_}')


Scikit-learn Linear regression R2 score: 0.9307237996010832
Scikit-learn Linear regression MAPE: 0.046665771765258775 

weights: (31734.098811233787, -107.40804717984585, 2168.8736968153985)
prediction: [46528.00800666 35018.47848628 49448.73803373 38604.36954966
 30788.13913983] 

scaled weights: (40922.38666080837, -1049.7866043343417, 8718.764356366162)

Визуализация множественной линейной регрессии с 2 признаками

feature1, feature2 = X1[:, 0], X1[:, 1]
X1_linspace = np.linspace(feature1.min(), feature1.max())
X2_linspace = np.linspace(feature2.min(), feature2.max())
X1_surface, X2_surface = np.meshgrid(X1_linspace, X2_linspace)
X_surfaces = np.array([X1_surface.ravel(), X2_surface.ravel()]).T

sk_linear_regression = LinearRegression()
sk_linear_regression.fit(X1_train, y1_train)
y_surface = sk_linear_regression.predict(X_surfaces).reshape(X1_surface.shape)

fig = plt.figure(figsize=(9, 7))
ax = plt.axes(projection='3d')
ax.scatter(feature1, feature2, y1, color='red', marker='o')
ax.plot_surface(X1_surface, X2_surface, y_surface, color='black', alpha=0.6)
plt.title('Fitted linear regression surface')
ax.set_xlabel('Age')
ax.set_ylabel('Experience')
ax.set_zlabel('Income')
ax.view_init(20, 10)
plt.show()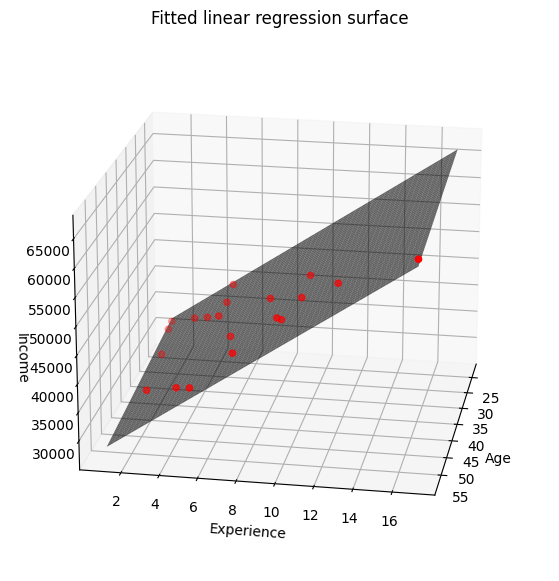

**Плоскость обученной линейной регрессии, проходящая через обучающий набор**

Полиномиальная регрессия

Линейную регрессию также можно применять к данным с нелинейной зависимостью, добавив степени каждого признака в виде новых признаков с последующим обучением на полученном датасете. Такой подход позволяет улавливать линейные связи в многомерном пространстве признаков и называется полиномиальной регрессией, а для преобразования признаков в полином степени n в scikit-learn имеется класс PolynomialFeatures, который кроме степеней каждого признака ещё добавляет их комбинации до заданной степени. Например, для признаков и со степенью 3 кроме и будут также добавлены их комбинации в виде и .

Стоит отметить, что полиномиальная регрессия всё ещё остаётся линейной, однако на графике в исходном пространстве признаков она будет выглядеть в виде кривой, поскольку полученная гиперплоскость в многомерном пространстве признаков будет соответствовать сложной кривой линии в исходном пространстве.

Загрузка датасета

Для обучения модели будет использован Ice Cream Selling dataset где необходимо выполнить прогнозирование продаж мороженого на основе данных о температуре.

df_path = "/content/drive/MyDrive/ice_cream_selling.csv"
ice_cream = pd.read_csv(df_path)
X2, y2 = ice_cream.iloc[:, :-1], ice_cream.iloc[:, -1]
X2_train, X2_test, y2_train, y2_test = train_test_split(X2, y2, random_state=0)
print(ice_cream.head())


   Temperature (°C)  Ice Cream Sales (units)
0         -4.662263                41.842986
1         -4.316559                34.661120
2         -4.213985                39.383001
3         -3.949661                37.539845
4         -3.578554                32.284531

Обучение полиномиальной регрессии и оценка полученных результатов

Как можно заметить, в данном случае линейная регрессия не способна описать взаимосвязь в исходных данных должным образом и имеет высокую ошибку, однако после добавления полиномиальных признаков результат получился довольно хорошим.

С другой стороны, если использовать полином слишком высокой степени, то модель будет явно переобучена, а если низкой, то недообучена. Для решения данной проблемы необходимо использовать перебор нескольких полиномов для выбора оптимальной кривизны линии, описывающей взаимосвязь в данных наилучшим образом.

feature_name, target_name = ice_cream.columns
poly_features = PolynomialFeatures(degree=8, include_bias=True)
X2_poly = poly_features.fit_transform(X2)
X2_poly_train, X2_poly_test = train_test_split(X2_poly, random_state=0)

sk_linear_regression = LinearRegression()
sk_linear_regression.fit(X2_train, y2_train)
sk_lr_pred_res = sk_linear_regression.predict(X2_test)
sk_lr_pred_all_data_res = sk_linear_regression.predict(X2)

sk_polynomial_regression = LinearRegression()
sk_polynomial_regression.fit(X2_poly_train, y2_train)
sk_poly_lr_pred_res = sk_polynomial_regression.predict(X2_poly_test)
sk_poly_lr_pred_all_data_res = sk_polynomial_regression.predict(X2_poly)

linear_regression_r2 = r2_score(y2_test, sk_lr_pred_res)
polynomial_regression_r2 = r2_score(y2_test, sk_poly_lr_pred_res)

linear_regression_mse = mean_squared_error(y2_test, sk_lr_pred_res)
polynomial_regression_mse = mean_squared_error(y2_test, sk_poly_lr_pred_res)

linear_regression_mape = mean_absolute_percentage_error(y2_test, sk_lr_pred_res)
polynomial_regression_mape = mean_absolute_percentage_error(y2_test, sk_poly_lr_pred_res)

print(f'R2 score (Linear regression): {linear_regression_r2}')
print(f'R2 score (Polynomial regression): {polynomial_regression_r2}', '\n')

print(f'MSE (Linear regression): {linear_regression_mse}')
print(f'MSE (Polynomial regression): {polynomial_regression_mse}', '\n')

print(f'MAPE (Linear regression): {linear_regression_mape}')
print(f'MAPE (Polynomial regression): {polynomial_regression_mape}')

plt.scatter(X2, y2)
plt.plot(X2, sk_lr_pred_all_data_res, color='darkorange', label='Linear Regression')
plt.plot(X2, sk_poly_lr_pred_all_data_res, color='green', label='Polynomial Regression')
plt.title('Polynomial vs Linear regression')
plt.xlabel(feature_name)
plt.ylabel(target_name)
plt.legend()
plt.show()


R2 score (Linear regression): -0.17464074069095403
R2 score (Polynomial regression): 0.926383512778148 

MSE (Linear regression): 104.58329195064105
MSE (Polynomial regression): 6.554390894849093 

MAPE (Linear regression): 3.6799207393653273
MAPE (Polynomial regression): 0.4288439423788508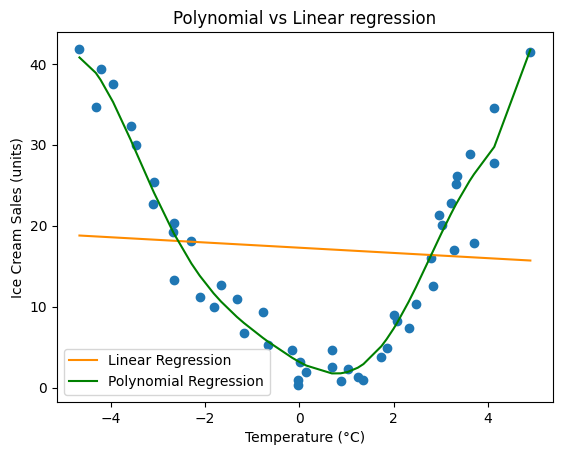

Регуляризация линейной регрессии (Ridge, Lasso, ElasticNet)

Если в полиномиальной регрессии регуляризация позволяет уменьшить кривизну линии через снижение количества полиномиальных степеней, то в случае с линейной регрессией регуляризация будет заключаться в изменении наклона линии путём ограничения весов модели, обменивая более высокое смещение на низкую дисперсию.

Гребневая регрессия (Ridge regression) или регуляризация Тихонова применяется в случае мультиколлинеарности через добавление L2-регуляризации к функции потерь во время обучения и сильнее всего занижает веса для признаков с высокой корреляцией: их значения будут приближаться к нулю, но никогда его не достигнут. Лучше всего применять гребневую регрессию после стандартизации признаков.

$J += \alpha \sum \limits_{i=1}^{n} w_i^2$

Лассо-регрессия (Lasso regression или Least Absolute Shrinkage & Selection Operator) обычно используется для отбора признаков через добавление L1-регуляризации к функции потерь во время обучения. Проще говоря, лассо-регрессия стремится уменьшить число параметров модели путем зануления весов для неинформативных и избыточных признаков, что на выходе даст разреженную модель (с небольшим числом ненулевых весов признаков).

$J += \alpha \sum \limits_{i=1}^{n} |w_i|$

Эластичная сеть (ElasticNet) представляет собой комбинацию L1 и L2-регуляризаций через отношение их смеси r, что может принести особую пользу в ситуациях, когда в данных необходимо одновременно выполнять отбор признаков и бороться с мультиколлинеарностью. В Scikit-Learn для управления смесью Ridge и Lasso используется "l1_ratio".

$J = MSE(w) + r\alpha \sum \limits_{i=1}^{n} |w_i| + \frac{1 - r}{2} \alpha \sum \limits_{i=1}^{n} w_i^2$

Кроме того, в качестве регуляризации линейной регрессии ещё можно использовать раннюю остановку (early stopping), которая заключаются в прекращении обучения модели после определённого количества итераций или достижения заданного уровня ошибки на валидационной выборке. Однако при использовании стохастического или мини-пакетного градиентного спуска в данном случае могут возникнуть трудности в поиске минимальной ошибки из-за менее гладких кривых обучения.

Стоит также отметить, что приведённые выше методы регуляризации нередко показывают хороший прирост в точности на зашумленных данных, а в случае с полиномиальными признаками можно достичь чуть меньшего искривления линии, что также позволит увеличить обобщающую способность модели.

Загрузка датасета

X3, y3 = make_regression(n_samples=14, n_features=1, noise=2, random_state=0)
X3_train, X3_test, y3_train, y3_test = train_test_split(X3, y3, random_state=0)
print('X3', X3, sep='\n')
print('y3', y3, sep='\n')


X3
[[ 0.12167502]
 [-0.10321885]
 [-0.15135721]
 [ 2.2408932 ]
 [ 0.40015721]
 [ 0.14404357]
 [ 1.45427351]
 [ 0.95008842]
 [ 0.4105985 ]
 [-0.97727788]
 [ 1.86755799]
 [ 0.76103773]
 [ 1.76405235]
 [ 0.97873798]]
y3
[ 3.89311392 -0.66634818 -0.321328   18.73883123  4.00084003 -2.10376463
  9.19719051  4.82754439  4.2778644  -6.3918002  12.51745243  4.92181298
 13.49975682  6.58940369]

Обучение моделей и оценка полученных результатов

Как можно заметить, в данном случае ElasticNet имеет самую высокую точность среди всех видов регуляризации, что обусловлено лучшим увеличением обобщающей способности за счёт более сильных штрафов во время обучения. На графике ниже видно, что это достигается за счёт более сильного наклона красной линии.

Linear regression (scikit-learn)

sk_linear_regression = LinearRegression()
sk_linear_regression.fit(X3_train, y3_train)

sk_lr_pred_res = sk_linear_regression.predict(X3_test)
sk_lr_pred_train_res = sk_linear_regression.predict(X3_train)

sk_lr_r2 = r2_score(y3_test, sk_lr_pred_res)
sk_lr_train_r2 = r2_score(y3_train, sk_lr_pred_train_res)

sk_lr_mse = mean_squared_error(y3_test, sk_lr_pred_res)
sk_lr_train_mse = mean_squared_error(y3_train, sk_lr_pred_train_res)

sk_lr_mape = mean_absolute_percentage_error(y3_test, sk_lr_pred_res)
sk_lr_train_mape = mean_absolute_percentage_error(y3_train, sk_lr_pred_train_res)

print(f'Linear regression R2 score: {sk_lr_r2}')
print(f'Linear regression train R2 score: {sk_lr_train_r2}', '\n')

print(f'Linear regression MSE: {sk_lr_mse}')
print(f'Linear regression train MSE: {sk_lr_train_mse}', '\n')

print(f'Linear regression MAPE: {sk_lr_mape}')
print(f'Linear regression train MAPE: {sk_lr_train_mape}', '\n')

print(f'prediction: {sk_lr_pred_res}')


Linear regression R2 score: 0.6982257627953212
Linear regression train R2 score: 0.9427934415059153 

Linear regression MSE: 1.335733574978215
Linear regression train MSE: 3.214557953209687 

Linear regression MAPE: 0.21244193731317745
Linear regression train MAPE: 0.5606808073073533 

prediction: [ 3.05512157 10.71540836  2.97848536  5.62724885]

Ridge regression (scikit-learn)

sk_ridge_regression = Ridge()
sk_ridge_regression.fit(X3_train, y3_train)

sk_ridge_pred_res = sk_ridge_regression.predict(X3_test)
sk_ridge_pred_train_res = sk_ridge_regression.predict(X3_train)

sk_ridge_r2 = r2_score(y3_test, sk_ridge_pred_res)
sk_ridge_train_r2 = r2_score(y3_train, sk_ridge_pred_train_res)

sk_ridge_mse = mean_squared_error(y3_test, sk_ridge_pred_res)
sk_ridge_train_mse = mean_squared_error(y3_train, sk_ridge_pred_train_res)

sk_ridge_mape = mean_absolute_percentage_error(y3_test, sk_ridge_pred_res)
sk_ridge_train_mape = mean_absolute_percentage_error(y3_train, sk_ridge_pred_train_res)

print(f'Ridge R2 score: {sk_ridge_r2}')
print(f'Ridge train R2 score: {sk_ridge_train_r2}', '\n')

print(f'Ridge MSE: {sk_ridge_mse}')
print(f'Ridge train MSE: {sk_ridge_train_mse}', '\n')

print(f'Ridge MAPE: {sk_ridge_mape}')
print(f'Ridge train MAPE: {sk_ridge_train_mape}', '\n')

print(f'prediction: {sk_ridge_pred_res}')


Ridge R2 score: 0.8201023267367127
Ridge train R2 score: 0.9347612375917475 

Ridge MSE: 0.7962752700962114
Ridge train MSE: 3.665904540974796 

Ridge MAPE: 0.17278003508553688
Ridge train MAPE: 0.44961917938852436 

prediction: [ 3.24001681 10.1932471   3.17045424  5.5747327 ]

Lasso regression (scikit-learn)

sk_lasso_regression = Lasso()
sk_lasso_regression.fit(X3_train, y3_train)

sk_lasso_pred_res = sk_lasso_regression.predict(X3_test)
sk_lasso_pred_train_res = sk_lasso_regression.predict(X3_train)

sk_lasso_r2 = r2_score(y3_test, sk_lasso_pred_res)
sk_lasso_train_r2 = r2_score(y3_train, sk_lasso_pred_train_res)

sk_lasso_mse = mean_squared_error(y3_test, sk_lasso_pred_res)
sk_lasso_train_mse = mean_squared_error(y3_train, sk_lasso_pred_train_res)

sk_lasso_mape = mean_absolute_percentage_error(y3_test, sk_lasso_pred_res)
sk_lasso_train_mape = mean_absolute_percentage_error(y3_train, sk_lasso_pred_train_res)

print(f'Lasso R2 score: {sk_lasso_r2}')
print(f'Lasso train R2 score: {sk_lasso_train_r2}', '\n')

print(f'Lasso MSE: {sk_lasso_mse}')
print(f'Lasso train MSE: {sk_lasso_train_mse}', '\n')

print(f'Lasso MAPE: {sk_lasso_mape}')
print(f'Lasso train MAPE: {sk_lasso_train_mape}', '\n')

print(f'prediction: {sk_lasso_pred_res}')


Lasso R2 score: 0.8664469300530337
Lasso train R2 score: 0.9246970466502308 

Lasso MSE: 0.5911416468881094
Lasso train MSE: 4.231432793072299 

Lasso MAPE: 0.1529096993850169
Lasso train MAPE: 0.47581220410842373 

prediction: [3.33264803 9.93164796 3.2666293  5.54842248]

ElasticNet regression (scikit-learn)

sk_elastic_net_regression = ElasticNet()
sk_elastic_net_regression.fit(X3_train, y3_train)

sk_elastic_net_pred_res = sk_elastic_net_regression.predict(X3_test)
sk_elastic_net_pred_train_res = sk_elastic_net_regression.predict(X3_train)

sk_elastic_net_r2 = r2_score(y3_test, sk_elastic_net_pred_res)
sk_elastic_net_train_r2 = r2_score(y3_train, sk_elastic_net_pred_train_res)

sk_elastic_net_mse = mean_squared_error(y3_test, sk_elastic_net_pred_res)
sk_elastic_net_train_mse = mean_squared_error(y3_train, sk_elastic_net_pred_train_res)

sk_elastic_net_mape = mean_absolute_percentage_error(y3_test, sk_elastic_net_pred_res)
sk_elastic_net_train_mape = mean_absolute_percentage_error(y3_train, sk_elastic_net_pred_train_res)

print(f'ElasticNet R2 score: {sk_elastic_net_r2}')
print(f'ElasticNet train R2 score: {sk_elastic_net_train_r2}', '\n')

print(f'ElasticNet MSE: {sk_elastic_net_mse}')
print(f'ElasticNet train MSE: {sk_elastic_net_train_mse}', '\n')

print(f'ElasticNet MAPE: {sk_elastic_net_mape}')
print(f'ElasticNet train MAPE: {sk_elastic_net_train_mape}', '\n')

print(f'prediction: {sk_elastic_net_pred_res}')


ElasticNet R2 score: 0.9482289494488992
ElasticNet train R2 score: 0.8045065979219737 

ElasticNet MSE: 0.2291525316195137
ElasticNet train MSE: 10.985189233414891 

ElasticNet MAPE: 0.0831221231617497
ElasticNet train MAPE: 1.2542789122808766 

prediction: [3.82230425 8.54881346 3.77501858 5.40934447]

Визуализация снижения ошибок линейной регрессии и её регуляризаций

train_r2_scores = [sk_lr_train_r2, sk_ridge_train_r2, sk_lasso_train_r2, sk_elastic_net_train_r2]
test_r2_scores = [sk_lr_r2, sk_ridge_r2, sk_lasso_r2, sk_elastic_net_r2]

train_mses = [sk_lr_train_mse, sk_ridge_train_mse, sk_lasso_train_mse, sk_elastic_net_train_mse]
test_mses = [sk_lr_mse, sk_ridge_mse, sk_lasso_mse, sk_elastic_net_mse]

fig = plt.figure()
ax1 = fig.add_subplot(221)
ax1.title.set_text('R2 reduction')
ax1.set_xlabel('R2 train')
ax1.set_ylabel('test')
ax1.scatter(train_r2_scores, test_r2_scores, color='red')
ax1.plot(train_r2_scores, test_r2_scores)

ax2 = fig.add_subplot(222)
ax2.title.set_text('MSE reduction')
ax2.set_xlabel('MSE train')
ax2.scatter(train_mses, test_mses, color='red')
ax2.plot(train_mses, test_mses)

Графики линейной регрессии и её регуляризаций

sk_linear_regression_pred_all_data_res = sk_linear_regression.predict(X3)
sk_ridge_regression_pred_all_data_res = sk_ridge_regression.predict(X3)
sk_lasso_regression_pred_all_data_res = sk_lasso_regression.predict(X3)
sk_elastic_net_regression_all_data_pred_res = sk_elastic_net_regression.predict(X3)

plt.scatter(X3, y3, color='black')
plt.plot(X3, sk_linear_regression_pred_all_data_res, label='Linear regression')
plt.plot(X3, sk_ridge_regression_pred_all_data_res, label='Ridge')
plt.plot(X3, sk_lasso_regression_pred_all_data_res, label='Lasso')
plt.plot(X3, sk_elastic_net_regression_all_data_pred_res, label='ElasticNet')
plt.title('Regression regularizations comparison')
plt.xlabel('X3')
plt.ylabel('y3')
plt.legend()
plt.show()

Преимущества и недостатки линейной регрессии

Преимущества:

простота в реализации и интерпретации;
высокая скорость работы;
относительно хорошая точность в случае с линейной зависимостью в данных.

Недостатки:

низкая гибкость и адаптивность из-за предположения о линейности данных;
низкая точность в случае с данными сложной формы, что следует из предыдущего пункта;
чувствительность к шуму и выбросам.

Стоит отметить, что перечисленные недостатки касаются классического случая и могут быть частично либо полностью устранены с помощью вышеописанных методов. Однако на сегодняшний день существует ряд более стабильных и эффективных алгоритмов, применяемых в классическом машинном обучении.

Дополнительные источники

Документация:

Видео про линейную и полиномиальную регрессии: один, два, три.

Видео про регуляризацию: один, два, три, четыре, пять.

Логистическая и Softmax-регрессии ?

Комментарии (11)

dyadyaSerezha
30.03.2024 19:44
#26669683
Что автор имел ввиду под выражением "реализация с нуля"?
1. Ctochastik
  30.03.2024 19:44
  #26669785
  Тоже улыбнуло) Например, можно было в выводе least squares normal equation более подробно расписать матричное дифференцирование по весам, чтобы читатели понимали откуда что
  1. egaoharu_kensei Автор
    30.03.2024 19:44
    #26669809
    Можете уточнить в каком именно месте вывод недостаточно подробен и что под этим имеется в виду?
    
    Ctochastik
    30.03.2024 19:44
    #26670551
    Имею в виду появление 2 вместо wT в первом слагаемом в скобках.
    
    egaoharu_kensei Автор
    30.03.2024 19:44
    #26670757
    Конечно можно написать, что производная квадрата равна двойке, но стоит ли? Думаю, что люди, занимающиеся ML, и так в курсе об этом.
    
    haqreu
    30.03.2024 19:44
    #26670893
    Производная x^2 равна не 2, а 2x, если что.
    
    egaoharu_kensei Автор
    30.03.2024 19:44
    #26671093
    Всё верно, поэтому в формуле остался один вектор весов. Уточню, что в данном случае производная берётся не по , если что :)
    
    Вопрос же был про появление двойки, поэтому я и ответил только про неё, или на ваш взгляд, люди, читающие статьи по ML, не знакомы с производными и эту тему стоит раскрыть более подробно? Лично мне так не кажется.
    
    haqreu
    30.03.2024 19:44
    #26671121
    +1
    Да ладно вам, дайте уже придраться ;)
    
    Я-то свои плюсы поставил.
    
    egaoharu_kensei Автор
    30.03.2024 19:44
    #26671517
    +1
    ну ладно :)
    
    grmile
    30.03.2024 19:44
    #26671425
    +1
    Когда я увидел "с нуля", я почитал статью. Думаю на "с нуля" такие как я и ведутся: я не занимаюсь МЛ, мне просто интересна эта тема. И вот если производные и интегралы я ещё помню, то матрицы я видел 26 лет назад, на первом курсе института, и переход от слу к матрицам для меня выглядел непонятно. Я , конечно же начал гуглить нормальное уравнение, но там тоже не опускаются до такого уровня.
    Что же касается людей занимающихся МЛ, то думаю что они в курсе и о линейной регрессии, раз уж помнят правила производных.
    
    Тем не менее, спасибо, в процессе гугления я узнал/напомнил много нового: и Крамера и детерминант и обратную матрицу.
    
    egaoharu_kensei Автор
    30.03.2024 19:44
    #26671539
    Дело конечно же ваше, но лучше перед ML освежить знания по математике, чтобы потом было легче. К слову, я про это тоже писал план обучения, с которым можно ознакомиться здесь.