Логистическая и Softmax-регрессии. Основная идея и реализация с нуля на Python / forpes.ru

Главная
Логистическая и Softmax-регрессии. Основная идея и реализация с нуля на Python

Логистическая и Softmax-регрессии. Основная идея и реализация с нуля на Python

28.03.2024 10:06

egaoharu_kensei 0 1600 Источник

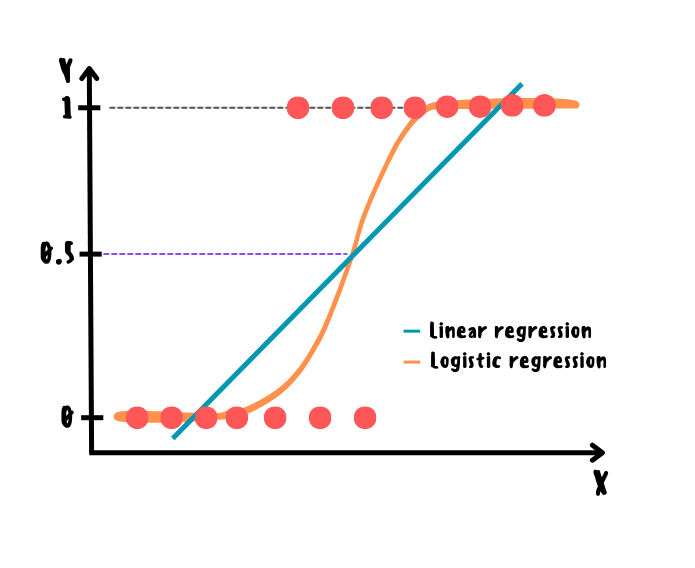
Начнём с более простого. Логистическая регрессия — линейный бинарный классификатор, основанный на применении сигмоидальной функции к линейной комбинации признаков, результатом которого является вероятность принадлежности к определённому классу. Обычно порог устанавливается 0.5: если вероятность меньше порога — класс относится к 0, а если больше — к 1. В принципе, условия определения логистической регрессии такие же как и у линейной за исключением бинаризации таргета.

Ноутбук с данными алгоритмами можно загрузить на Kaggle (eng) и GitHub (rus).

Поскольку прогноз в линейной регрессии может принимать значения в любом диапазоне, а нам нужны вероятности принадлежности к классу в диапазоне [0; 1], то прогноз линейной регрессии можно представить в виде логарифма шансов (шанс — это отношение вероятности выполнения события к его невыполнению) и уже из него выразить вероятность принадлежности к классу. Полученная функция называется сигмоидальной.

$\ln(\frac{p_+}{1 - p_+}) = w \cdot x + b$ $\frac{p_+}{1 - p_+} = e^{w \cdot x + b} \ \ \Rightarrow \ \ p_+ = \frac{1}{1 + e^{-(w \cdot x + b)}} = \sigma(w \cdot x + b)$

**Линейная vs логистическая регрессия при прогнозировании класса**

Функция потерь и метод максимального правдоподобия

Выбор линии (плоскости) для разделения классов наилучшим образом заключается в минимизации усреднённой логистической функции потерь, основанной на оптимизации метода максимального правдоподобия. Суть данного метода заключается в поиске параметров модели, которые будут соответствовать наблюдениям с максимальной вероятностью, а его оптимизация заключается в логарифме правдоподобия вместо правдоподобия из-за вычислительной эффективности и более стабильных результатов. Проще говоря, функция потерь просто является средними потерями на всём обучающем наборе.

Поскольку в данном случае отсутствует решение в аналитическом виде, а функция потерь является гладкой и выпуклой, то обучение логистической регрессии происходит также на основе градиентного спуска как и в случае линейной регрессии.

Вывод уравнения логистической регрессии и градиента её функции потерь

Изначальная форма логистических потерь:

$\begin{equation} L(\sigma(z), y_i) = \begin{cases} - \ln\sigma(z) & \text{if $y_i=1$}\\ - \ln(1 - \sigma(z)) & \text{if $y_i=0$} \end{cases} \end{equation}$

Метод максимального правдоподобия:

$L(\sigma(z), y_i) = \prod\limits_{i=1}^{n} σ(z)^{y_i} (1 - \sigma(z))^{(1-y_i)}$

Логистические потери с логарифмом подобия:

$L_{log}(\sigma(z), y_i) = -[y_i\ln\sigma(z) + (1 - y_i)\ln(1 - \sigma(z))]$

Функция потерь для всего обучающего набора:

$J(w, b) = \frac{1}{n} \sum\limits_{i = 1}^{n} L_{log}(\sigma(z), y_i)$

Градиенты функции потерь для смещения и весов соответственно:

$\frac{\partial J(w, b)}{\partial b} = (\frac{1}{n} \sum\limits_{i = 1}^{n} L_{log}(\sigma(z), y_i))' = \frac{1}{n} \sum\limits_{i = 1}^{n} \frac{\partial{L_{log}(\sigma(z), y_i)}}{\partial{b}} = \frac{1}{n} \sum\limits_{i = 1}^{n} (\sigma(z) - y_i)$ $\frac{\partial J(w, b)}{\partial \omega} = (\frac{1}{n} \sum\limits_{i = 1}^{n} L_{log}(\sigma(z), y_i))' = \frac{1}{n} \sum\limits_{i = 1}^{n} \frac{\partial{L_{log}(\sigma(z), y_i)}}{\partial{\omega}} = \frac{1}{n} \sum\limits_{i = 1}^{n} (\sigma(z) - y_i)x_i$

Ниже приведены расчёты частных производных логистических потерь для смещения и весов соответственно:

$\frac{\partial{L_{log}(\sigma(z), y_i)}}{\partial{b}} = \frac{\partial{L_{log}(\sigma(z), y_i)}}{\partial{\sigma(z)}} \cdot \frac{\partial{\sigma(z)}}{\partial{z}} \cdot \frac{\partial{z}}{\partial{b}}$ $\frac{\partial{L_{log}(\sigma(z), y_i)}}{\partial{\omega}} = \frac{\partial{L_{log}(\sigma(z), y_i)}}{\partial{\sigma(z)}} \cdot \frac{\partial{\sigma(z)}}{\partial{z}} \cdot \frac{\partial{z}}{\partial{\omega}}$ $\frac{\partial{L_{log}(\sigma(z), y_i)}}{\partial{\sigma(z)}} = -[y_i(\ln\sigma(z))' + (1 - y_i)(\ln(1 - \sigma(z)))'] = \\ = -[y_i \cdot \frac{1}{\sigma(z)} + (1 - y_i) \cdot \frac{1}{1-\sigma(z)} \cdot (-1)] = \\ = \frac{1 - y_i}{1 - \sigma(z)} - \frac{y_i}{\sigma(z)} = \frac{\sigma(z) - \sigma(z) y_i - y_i + \sigma(z) y_i}{\sigma(z) (1 - \sigma(z)} = \frac{\sigma(z) - y_i}{\sigma(z)(1 - \sigma(z))}$ $\frac{\partial{\sigma(z)}}{\partial{z}} = ((1 + e^{-z})^{-1})' = \frac{-1}{(1 + e^{-z})^{-2}} \cdot e^{-z} \cdot (-1) = \frac{e^{-z}}{(1 + e^{-z})^{-2}} = \\ = |e^{-z} = \frac{1}{\sigma(z)} - 1 = \frac{1-\sigma(z)}{\sigma(z)}| = \frac{1 - \sigma(z)}{\sigma(z)(1 + \frac{1 - \sigma(z)}{\sigma(z)})^{2}} = \sigma(z)(1 - \sigma(z))$ $\frac{\partial z}{\partial b} = (w \cdot x_i)' + b' = 0 + 1 = 1$ $\frac{\partial z}{\partial \omega} = w' \cdot x_i + w \cdot x_i' + b' = x_i + 0 + 0 = x_i$ $\frac{\partial{L_{log}(\sigma(z), y_i)}}{\partial{b}} = \frac{\sigma(z) - y_i}{\sigma(z)(1 - \sigma(z))} \cdot \sigma(z)(1 - \sigma(z)) = \sigma(z) - y_i$ $\frac{\partial{L_{log}(\sigma(z), y_i)}}{\partial{\omega}} = \frac{\sigma(z) - y_i}{\sigma(z)(1 - \sigma(z))} \cdot \sigma(z)(1 - \sigma(z)) \cdot x_i = (\sigma(z) - y_i)x_i$

Где:

$\sigma(z) = \frac{1}{1 + e^{-z}}$ — сигмоидальная функция;
$z_{w, b}(x_i) = w \cdot x_i + b$ — линейная функция;
— смещение;
— вектор весов;
— вектор признаков i-го образца.

Принцип работы логистической регрессии

Как можно было догадаться, обучение логистической регрессии происходит идентично линейной за исключением пропуска линейных прогнозов через сигмоидальную функцию на каждой итерации. С помощью полученных весов сначала выполняется линейный прогноз, а затем итоговый через сигмоидальную функцию: полученные вероятности округляются согласно заданному порогу (обычно 0.5).

Стоит также отметить, что для логистической регрессии характерны такие же особенности в плане оптимизации и регуляризации, как и для линейной.

Softmax-regression

Логистическую регрессию можно также обобщить для многоклассовой классификации. Для этого существуют 2 стратегии:

one vs rest, когда обучается модель для каждого уникального класса в таргете на основе бинаризации и в качестве итогового прогноза выбирается класс с максимальной вероятностью;
softmax, когда одна модель поддерживает много классов напрямую, что мы сейчас и рассмотрим более подробно.

Идея softmax-регрессии заключается в следующем: сначала производится бинаризация таргета с помощью one-hot и для признаков строится таблица весов количестве, пропорциональному числу уникальных значений в таргете. Далее вычисляется линейный прогноз с учётом весов для каждого класса, после чего полученные результаты оцениваются как вероятность класса от 0 до 1 с помощью функции softmax, которая также ещё называется нормализованной экспоненциальной.

В данном случае в качестве функции потерь будет выступать перекрёстная энтропия (cross-entropy) поскольку она штрафует модель в случае низкой оценки вероятности для целевого класса. Другими словами, кросс-энтропия используется для оценки качества соответствия набора оценочных вероятностей классов целевым классам. Итоговым прогнозом на тестовой выборке будет класс с максимальной вероятностью.

Формулы для расчётов

Линейный прогноз для класса :

$z_k (x^{(i)}) = w_k \cdot x^{(i)} + b_k$

Функция softmax:

$p_k = \frac{e^{z_k (x^{(i)})}}{\sum \limits_{j=1}^{K} e^{z_j (x^{(i)})}}$

Функция потерь:

$J(\Theta) = - \frac{1}{n} \sum \limits_{i=1}^{n} \sum \limits_{k=1}^{K} y_k^{(i)} log(\hat p_k^{(i)})$

Градиент смещения для класса :

$\frac{\partial J(\Theta)}{\partial b_k} = \frac{1}{n} \sum \limits_{i=1}^{n} (\hat p_k^{(i)} - y_k^{(i)})$

Вектор-градиент весов для класса :

$\frac{\partial J(\Theta)}{\partial w_k} = \frac{1}{n} \sum \limits_{i=1}^{n} (\hat p_k^{(i)} - y_k^{(i)}) x^{(i)}$

Где:

— число классов;
$\Theta$ — матрица параметров.

Как можно заметить, по сути, softmax представляет собой более быструю оптимизацию one vs rest, позволяющую избежать обучение лишних моделей, что будет особенно полезно при работе с большими датасетами. Ещё одно интересное наблюдение заключается в том, что при наличии только двух классов в таргете (k=2) функция потерь будет эквивалентна log loss в логистической регрессии для бинарного случая.

Импорт необходимых библиотек

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler, LabelEncoder
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
from mlxtend.plotting import plot_decision_regions

Реализация на Python с нуля

Логистическая регрессия

class GDLogisticRegression:
    def __init__(self, learning_rate=0.1, tolerance=0.0001, max_iter=1000):
        self.learning_rate = learning_rate
        self.tolerance = tolerance
        self.max_iter = max_iter

    def fit(self, X, y):
        n_samples, n_features = X.shape
        self.bias, self.weights = 0, np.zeros(n_features)
        previous_db, previous_dw = 0, np.zeros(n_features)

        for _ in range(self.max_iter):
            y_pred_linear = X @ self.weights + self.bias
            y_pred_sigmoid = 1 / (1 + np.exp(-y_pred_linear))
            db = 1 / n_samples * np.sum(y_pred_sigmoid - y)
            dw = 1 / n_samples * X.T @ (y_pred_sigmoid - y)

            self.bias -= self.learning_rate * db
            self.weights -= self.learning_rate * dw
            abs_db_reduction = np.abs(db - previous_db)
            abs_dw_reduction = np.abs(dw - previous_dw)

            if abs_db_reduction < self.tolerance:
                if abs_dw_reduction.all() < self.tolerance:
                    break

            previous_db = db
            previous_dw = dw

    def predict(self, X_test):
        y_pred_linear = X_test @ self.weights + self.bias
        y_pred_sigmoid = 1 / (1 + np.exp(-y_pred_linear))
        classes = np.array([0 if pred < 0.5 else 1 for pred in y_pred_sigmoid])

        return classes

Softmax-регрессия

class SoftmaxRegression:
    def __init__(self, learning_rate=0.1, tolerance=0.0001, max_iter=1000):
        self.learning_rate = learning_rate
        self.tolerance = tolerance
        self.max_iter = max_iter

    def _softmax(self, predictions):
        exp = np.exp(predictions)

        return exp / np.sum(exp, axis=1, keepdims=True)

    def fit(self, X, y):
        n_classes = len(np.unique(y))
        n_samples, n_features = X.shape
        one_hot_y = pd.get_dummies(y).to_numpy()

        self.bias = np.zeros(n_classes)
        self.weights = np.zeros((n_features, n_classes))
        previous_db = np.zeros(n_classes)
        previous_dw = np.zeros((n_features, n_classes))

        for _ in range(self.max_iter):
            y_pred_linear = X @ self.weights + self.bias
            y_pred_softmax = self._softmax(y_pred_linear)
            db = 1 / n_samples * np.sum(y_pred_softmax - one_hot_y, axis=0)   # sum by columns
            dw = 1 / n_samples * X.T @ (y_pred_softmax - one_hot_y)

            self.bias -= self.learning_rate * db
            self.weights -= self.learning_rate * dw
            abs_db_reduction = np.abs(db - previous_db)
            abs_dw_reduction = np.abs(dw - previous_dw)

            if abs_db_reduction.all() < self.tolerance:
                if abs_dw_reduction.all() < self.tolerance:
                    break

            previous_db = db
            previous_dw = dw

    def predict(self, X_test):
        y_pred_linear = X_test @ self.weights + self.bias
        y_pred_softmax = self._softmax(y_pred_linear)
        most_prob_classes = np.argmax(y_pred_softmax, axis=1)

        return most_prob_classes

Код для отрисовки графика

def decision_boundary_plot(X, y, X_train, y_train, clf, feature_indexes, title=None):
    feature1_name, feature2_name = X.columns[feature_indexes]
    X_feature_columns = X.values[:, feature_indexes]
    X_train_feature_columns = X_train.values[:, feature_indexes]
    clf.fit(X_train_feature_columns, y_train.values)

    plot_decision_regions(X=X_feature_columns, y=y.values, clf=clf)
    plt.xlabel(feature1_name)
    plt.ylabel(feature2_name)
    plt.title(title)

Загрузка датасетов

Для обучения логистической регрессии будет использован Heart Attack dataset, где необходимо спрогнозировать возникновение либо отсутствие сердечного приступа у пациентов, исходя из их показателей в анализах.

В случае softmax-регрессии используется Credit Score Classification Dataset для прогноза кредитного рейтинга людей на основе их возраста, дохода и так далее.

df_path = "/content/drive/MyDrive/heart_attack.csv"
heart_attack = pd.read_csv(df_path)
print(heart_attack.head())

X1, y1 = heart_attack.iloc[:, :-1], heart_attack.iloc[:, -1]
X1_scaled = StandardScaler().fit_transform(X1)
y1 = pd.Series(LabelEncoder().fit_transform(y1))

X1_train, X1_test, y1_train, y1_test = train_test_split(X1, y1, random_state=0)
X1_train_s, X1_test_s, y1_train, y1_test = train_test_split(X1_scaled, y1, random_state=0)


   age  sex  cp  trtbps  chol  fbs  restecg  thalachh  exng  oldpeak  slp  \
0   63    1   3     145   233    1        0       150     0      2.3    0   
1   37    1   2     130   250    0        1       187     0      3.5    0   
2   41    0   1     130   204    0        0       172     0      1.4    2   
3   56    1   1     120   236    0        1       178     0      0.8    2   
4   57    0   0     120   354    0        1       163     1      0.6    2   

   caa  thall  output  
0    0      1       1  
1    0      2       1  
2    0      2       1  
3    0      2       1  
4    0      2       1

df_path = "/content/drive/MyDrive/credit_score.csv"
credit_score = pd.read_csv(df_path)
print(credit_score.head())

X2, y2 = credit_score.iloc[:, :-1], credit_score.iloc[:, -1]
cat_features_list = X2.select_dtypes(include=['object']).columns
X2[cat_features_list] = X2[cat_features_list].apply(LabelEncoder().fit_transform)
X2_scaled = StandardScaler().fit_transform(X2)
y2 = pd.Series(LabelEncoder().fit_transform(y2))

X2_train, X2_test, y2_train, y2_test = train_test_split(X2, y2, random_state=0)
X2_train_s, X2_test_s, y2_train, y2_test = train_test_split(X2_scaled, y2, random_state=0)


   Age  Gender  Income            Education Marital Status  \
0   25  Female   50000    Bachelor's Degree         Single   
1   30    Male  100000      Master's Degree        Married   
2   35  Female   75000            Doctorate        Married   
3   40    Male  125000  High School Diploma         Single   
4   45  Female  100000    Bachelor's Degree        Married   

   Number of Children Home Ownership Credit Score  
0                   0         Rented         High  
1                   2          Owned         High  
2                   1          Owned         High  
3                   0          Owned         High  
4                   3          Owned         High

Обучение моделей и оценка полученных результатов

Логистическая регрессия показала довольно хороший результат, но не самый лучший. В первую очередь, это связано с некоторым шумом в данных и поскольку это всё же линейный классификатор, то можно сделать вывод, что он лучше всего работает с данными, где прослеживается ярко выраженное линейное разделение, что хорошо заметно на данных для случая с softmax-регрессией.

Logistic regression

logistic_regression = GDLogisticRegression()
logistic_regression.fit(X1_train_s, y1_train)
pred_res = logistic_regression.predict(X1_test_s)
accuracy = accuracy_score(y1_test, pred_res)

print(f'Logistic regression accuracy: {accuracy}')
print(f'prediction: {pred_res}')


Logistic regression accuracy: 0.8289473684210527
prediction: [0 1 1 0 0 0 0 0 0 0 1 1 0 1 1 1 0 1 0 1 1 0 0 0 1 1 0 0 1 1 1 0 1 1 1 1 0
 1 0 0 1 1 0 0 1 1 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 1 0 1 1 0
 0 1]

Logistic regression (scikit-learn)

sk_logistic_regression = LogisticRegression(penalty=None, max_iter=1000, multi_class='ovr')
sk_logistic_regression.fit(X1_train, y1_train)
sk_pred_res = sk_logistic_regression.predict(X1_test)
sk_accuracy = accuracy_score(y1_test, sk_pred_res)

print(f'sk Logistic regression accuracy: {sk_accuracy}')
print(f'prediction: {sk_pred_res}')

feature_indexes = [3, 9]
title1 = 'LogisticRegression surface'
decision_boundary_plot(X1, y1, X1_train, y1_train, sk_logistic_regression, feature_indexes, title1)


sk Logistic regression accuracy: 0.8289473684210527
prediction: [0 1 1 0 0 0 0 0 0 0 1 1 0 1 1 1 0 1 0 1 1 0 0 0 1 1 0 0 1 1 1 0 1 1 1 1 0
 1 0 0 1 1 0 0 1 1 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 1 0 1 1 0
 0 1]

Softmax-regression

softmax_regression = SoftmaxRegression()
softmax_regression.fit(X2_train_s, y2_train)
softmax_pred_res = softmax_regression.predict(X2_test_s)
softmax_accuracy = accuracy_score(y2_test, softmax_pred_res)

print(f'Softmax-regression accuracy: {softmax_accuracy}')
print(f'Softmax prediction: {softmax_pred_res}')


Softmax-regression accuracy: 0.975609756097561
Softmax prediction: [1 1 0 0 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 2 1 1 0 1 1 1 0 1 2 1 1 0
 1 0 1 1]

Softmax-regression (scikit-learn)

sk_softmax_regression = LogisticRegression(penalty=None, max_iter=1000, multi_class='multinomial')
sk_softmax_regression.fit(X2_train, y2_train)
sk_softmax_pred_res = sk_softmax_regression.predict(X2_test)
sk_softmax_accuracy = accuracy_score(y2_test, sk_softmax_pred_res)

print(f'sk Softmax-regression accuracy: {sk_softmax_accuracy}')
print(f'sk Softmax prediction: {sk_softmax_pred_res}')


sk Softmax-regression accuracy: 0.975609756097561
sk Softmax prediction: [1 1 0 0 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 2 1 1 0 1 1 1 0 1 2 1 1 0
 1 0 1 1]

Преимущества и недостатки логистической регрессии

Преимущества:

простота в реализации и интерпретации;
высокая скорость работы;
относительно хорошая точность в случае с линейной зависимостью в данных.

Недостатки:

низкая гибкость и адаптивность из-за предположения о линейности данных;
низкая точность в случае с данными сложной формы, что следует из предыдущего пункта;
чувствительность к шуму и выбросам.

Стоит отметить, что, как и в случае с линейной регрессией, перечисленные недостатки касаются реализации в чистом виде и могут быть частично либо полностью устранены с помощью методов регуляризации или добавления полиномиальных признаков. Однако на сегодняшний день существуют другие алгоритмы, которые значительно превосходят логистическую регрессию в плане точности и стабильности.