
Метод опорных векторов (Support Vector Machines или просто SVM) — мощный и универсальный набор алгоритмов для работы с данными любой формы, применяемый не только для задач классификации и регрессии, но и также для выявления аномалий. В данной статье будут рассмотрены основные подходы к созданию SVM, принцип работы, а также реализации с нуля его наиболее популярных разновидностей.
Ноутбук с данными алгоритмами можно загрузить на Kaggle (eng) и GitHub (rus).
Линейный случай SVM
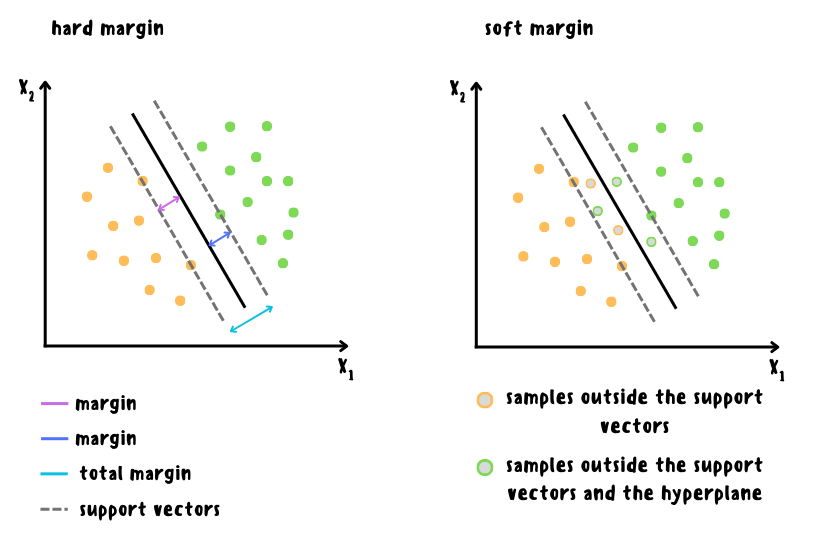
В случае линейной классификации основная идея SVM заключается в поиске гиперплоскости или линии, разделяющей классы наилучшим образом, а расположенные ближе всего к разделяющей гиперплоскости образцы называются опорными векторами. Лучшим разделением классов будет то, при котором максимизируется расстояние между опорными векторами и разделяющей гиперплоскостью. Это расстояние называется зазором. Здесь возможны 2 варианта:
1) Классификация с жёстким зазором (hard margin), когда все обучающие образцы должны быть правильно классифицированы и находиться за пределами полосы разделения. Такой подход работает только в случае хорошей линейной разделимости данных и является довольно чувствительным к выбросам.
2) Классификация с мягким зазором (soft margin), когда вводится допущение, что некоторые обучающие образцы могут нарушать условие правильной классификации или попадать в полосу разделения, но при этом вводится штраф за такие нарушения, пропорциональный параметру C (чем ниже данное значение, тем шире полоса и больше нарушений попадает в зазор). При таком подходе увеличивается обобщающая способность модели, что позволяет снизить риск переобучения.
Спрогнозированными классами будет линейная комбинация весов и тестовых признаков с использованием стратегии OVR (One-Versus-Rest) или OVA (One-Versus-All), а для минимизации используется функция потерь hinge.
В реализации scikit-learn к данной функции потерь ещё добавляется l1 или l2-регуляризация на выбор, а также имеется возможность использовать квадратичную функцию потерь с помощью параметра loss='squared_hinge'.
Стоит отметить, что задачи с жёстким и мягким зазором являются задачами выпуклой квадратичной оптимизации с линейными ограничениями и относятся к задачам квадратичного программирования, для решения которых существует множество различных готовых пакетов.
В данном случае используется готовая реализация на основе библиотеки Liblinear, но в ручной реализации ниже для более простого понимания будет использован градиентный спуск с одним улучшением: веса будут обновляться не на каждой итерации с учётом прогнозов всех образцов, а только с учётом прогнозов для каждого обучающего образца отдельно при условии, что размер отступа меньше 1, что получается из уравнения выше. Такой подход позволяет обеспечить сравнимую точность hinge loss без регуляризации с squared hinge loss с l2-регуляризацией в scikit-learn, а если использовать аналогичные параметры, то точность будет в целом немного выше, однако такое решение менее стабильно.
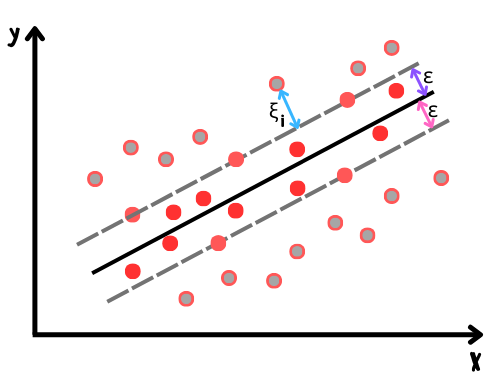
В случае линейной регрессии SVM пытается минимизировать расстояние между зазором и образцами, что лежат за его пределами, а добавление дополнительных обучающих образцов внутрь зазора не влияет на итоговый прогноз. Проще говоря, принцип такой же как и в обычной линейной регрессии, но вместо линии используется зазор, ширина которого контролируется параметром epsilon, а минимизируемая функция потерь называется epsilon-insensitive.
Как и в случае с классификацией, в реализации scikit-learn для регрессии SVM используется l1 или l2-регуляризация на выбор, а функция потерь также может быть квадратичной.
Нелинейный случай SVM
В случае нелинейной классификации данные преобразуются в пространство более высокой размерности, где они становятся линейно разделимыми. Одним из самых простых способов является добавление полиномиальных признаков, однако в таком случае сильно увеличивается вычислительная сложность.
Более интересным и эффективным способом является использование ядерного трюка — это приём работы с данными в исходном пространстве, при котором скалярное произведение трансформированных векторов n-й степени заменяется на их произведение в степени n, что даёт аналогичный результат. Проще говоря, такой подход позволяет получить такие же результаты, как и в случае с добавлением большого количества полиномиальных признаков без их фактического добавления:
где — полиномиальная отображающая функция степени
.
Ниже представлен пример ядерного трюка для полиномиальноrо отображения второй степени.

Функция, с помощью которой выполняется ядерный трюк, то есть определяется сходство между парами точек данных в исходном пространстве, называется ядром. В scikit-learn поддерживаются следующие ядра:
линейное — просто вычисляет скалярное произведение векторов в исходном пространстве, что эквивалентно обычному линейному классификатору:
полиномиальное — способно улавливать более сложные зависимости между данными, создавая оптимальную разделяющую гиперплоскость в новом пространстве, однако требуется тщательный подбор параметров :
гауссовское RBF (радиально-базисная функция) — хорошо подходит для случаев, когда отношение в данных имеет сложную нелинейную форму и менее подвержено переобучению, поскольку учитывает не только значения признаков, но и их распределение:
сигмоидальное — применяет гиперболический тангенс к линейной комбинации векторов, имитируя использование двухслойной нейронной сети с сигмоидальной функцией активации, что также позволяет хорошо работать со сложными нелинейными случаями, однако это может привести к переобучению в случае появления шума и выбросов:
В данном случае — параметр, определяющий степень влияния между обучающими образцами: чем ниже данное значение, тем больше радиус влияния образцов на формирование решающей границы, что делает её более гладкой. Между тем коэффициент сдвига
(coef0 в scikit-learn) влияет на гибкость ядра, что позволяет создавать более сложные решающие границы.
Стоит также добавить, что ядерный трюк может применяться не только в контексте SVM, но и к другим алгоритмам — просто так исторически сложилось, что ядерный трюк ассоциируется именно с SVM.
В случае нелинейной регрессии SVM также пытается сделать данные линейно разделимыми в пространстве более высокой размерности, но только для поиска оптимальной гиперплоскости, которая будет минимизировать расстояние между зазором и образцами как и в линейном случае.
В scikit-learn для работы с нелинейными случаями используются классы SVR и SVC на основе библиотеки Libsvm, в которой реализован алгоритм с поддержкой ядерного трюка и l2-регуляризацией, контролируемой параметром C.
Импорт необходимых библиотек
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mlxtend.plotting import plot_decision_regions
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, r2_score
from sklearn.utils import check_random_state, check_array
from sklearn.svm import LinearSVC, LinearSVR, SVC, SVR, _libsvm
from sklearn.datasets import load_iris, load_diabetes, load_wine, load_breast_cancerРеализация на Python с нуля
Linear SVM
class LinearSVM:
def __init__(self, regression=False, C=1.0, eps=0, learning_rate=0.001, max_iter=1000,
random_state=0):
self.regression = regression
self.C = C
self.eps = eps
self.learning_rate = learning_rate
self.max_iter = max_iter
self.random_state = random_state
def fit(self, X, y):
if self.regression:
self.bias, self.weights = self._find_weights(X, y)
else:
classes = np.unique(y)
n_classes = len(classes)
_, n_features = X.shape
self.bias = np.zeros(n_classes)
self.weights = np.zeros((n_classes, n_features))
np.random.seed(self.random_state)
for i, cls in enumerate(classes):
y_binary = np.where(y == cls, 1, -1)
self.bias[i], self.weights[i] = self._find_weights(X, y_binary)
def _find_weights(self, X, y):
n_samples, n_features = X.shape
bias = 0
weights = np.zeros(n_features) if self.regression else np.random.randn(n_features)
for _ in range(self.max_iter):
for i in range(n_samples):
y_pred = X[i] @ weights + bias
margin = y[i] - y_pred if self.regression else y[i] * y_pred
condition = np.abs(margin) > self.eps if self.regression else margin < 1
if condition:
if self.regression:
db = -self.C * (margin - self.eps)
dw = -self.C * (margin - self.eps) * X[i]
else:
db = -self.C * y[i]
dw = -self.C * y[i] * X[i]
bias -= self.learning_rate * db
weights -= self.learning_rate * dw
return bias, weights
def predict(self, X):
scores = X @ self.weights.T + self.bias
return scores if self.regression else np.argmax(scores, axis=1)Kernel SVM на основе Libsvm
class SVM:
def __init__(self, regression=False, C=1.0, kernel='rbf', degree=3, solver='auto',
gamma='scale', epsilon=0.1, coef0=0.0, shrinking=True, probability=False,
tol=0.001, cache_size=200, max_iter=-1, random_state=None):
self.regression = regression
self.C = C
self.kernel = kernel
self.degree = degree
self.solver = solver
self.gamma = gamma
self.epsilon = epsilon
self.coef0 = coef0
self.shrinking = shrinking
self.probability = probability
self.tol = tol
self.cache_size = cache_size
self.max_iter = max_iter
self.random_state = random_state
def fit(self, X, y):
X = X.astype(np.float64)
y = y.astype(np.float64)
rnd = check_random_state(self.random_state)
seed = rnd.randint(np.iinfo('i').max)
if self.gamma == 'scale':
self.gamma = 1.0 / (X.shape[1] * X.var()) if X.var() != 0 else 1.0
elif self.gamma == 'auto':
self.gamma = 1.0 / X.shape[1]
else:
self.gamma = self.gamma
if self.solver == 'auto':
self.solver = 'epsilon_svr' if self.regression else 'c_svc'
libsvm_impl = ['c_svc', 'nu_svc', 'one_class', 'epsilon_svr', 'nu_svr']
self.solver = libsvm_impl.index(self.solver)
(self.support_, self.support_vectors_, self._n_support, self.dual_coef_, self.intercept_,
self._probA, self._probB, self.fit_status_, self._num_iter
) = _libsvm.fit(X, y, C=self.C, svm_type=self.solver, kernel=self.kernel, gamma=self.gamma,
degree=self.degree, epsilon=self.epsilon, coef0=self.coef0, tol=self.tol,
shrinking=self.shrinking, probability=self.probability,
cache_size=self.cache_size, max_iter=self.max_iter, random_seed=seed
)
def predict(self, X_test):
X_test = X_test.astype(np.float64)
prediction = _libsvm.predict(X_test, self.support_, self.support_vectors_, self._n_support,
self.dual_coef_, self.intercept_, self._probA, self._probB,
svm_type=self.solver, kernel=self.kernel, degree=self.degree,
coef0=self.coef0, gamma=self.gamma, cache_size=self.cache_size
)
return prediction if self.regression else prediction.astype(int)Код для отрисовки графика
def decision_boundary_plot(X, y, X_train, y_train, clf, feature_indexes, title=None):
feature1_name, feature2_name = X.columns[feature_indexes]
X_feature_columns = X.values[:, feature_indexes]
X_train_feature_columns = X_train[:, feature_indexes]
clf.fit(X_train_feature_columns, y_train)
plot_decision_regions(X=X_feature_columns, y=y.values, clf=clf)
plt.xlabel(feature1_name)
plt.ylabel(feature2_name)
plt.title(title)Загрузка датасетов
X1, y1 = load_iris(return_X_y=True, as_frame=True)
X1_train, X1_test, y1_train, y1_test = train_test_split(X1.values, y1.values, random_state=0)
print(X1, y1, sep='\n')
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2
.. ... ... ... ...
145 6.7 3.0 5.2 2.3
146 6.3 2.5 5.0 1.9
147 6.5 3.0 5.2 2.0
148 6.2 3.4 5.4 2.3
149 5.9 3.0 5.1 1.8
[150 rows x 4 columns]
0 0
1 0
2 0
3 0
4 0
..
145 2
146 2
147 2
148 2
149 2
Name: target, Length: 150, dtype: int64X2, y2 = load_diabetes(return_X_y=True, as_frame=True)
X2_train, X2_test, y2_train, y2_test = train_test_split(X2.values, y2.values, random_state=0)
print(X2, y2, sep='\n')
age sex bmi bp s1 s2 s3 \
0 0.038076 0.050680 0.061696 0.021872 -0.044223 -0.034821 -0.043401
1 -0.001882 -0.044642 -0.051474 -0.026328 -0.008449 -0.019163 0.074412
2 0.085299 0.050680 0.044451 -0.005670 -0.045599 -0.034194 -0.032356
3 -0.089063 -0.044642 -0.011595 -0.036656 0.012191 0.024991 -0.036038
4 0.005383 -0.044642 -0.036385 0.021872 0.003935 0.015596 0.008142
.. ... ... ... ... ... ... ...
437 0.041708 0.050680 0.019662 0.059744 -0.005697 -0.002566 -0.028674
438 -0.005515 0.050680 -0.015906 -0.067642 0.049341 0.079165 -0.028674
439 0.041708 0.050680 -0.015906 0.017293 -0.037344 -0.013840 -0.024993
440 -0.045472 -0.044642 0.039062 0.001215 0.016318 0.015283 -0.028674
441 -0.045472 -0.044642 -0.073030 -0.081413 0.083740 0.027809 0.173816
s4 s5 s6
0 -0.002592 0.019907 -0.017646
1 -0.039493 -0.068332 -0.092204
2 -0.002592 0.002861 -0.025930
3 0.034309 0.022688 -0.009362
4 -0.002592 -0.031988 -0.046641
.. ... ... ...
437 -0.002592 0.031193 0.007207
438 0.034309 -0.018114 0.044485
439 -0.011080 -0.046883 0.015491
440 0.026560 0.044529 -0.025930
441 -0.039493 -0.004222 0.003064
[442 rows x 10 columns]
0 151.0
1 75.0
2 141.0
3 206.0
4 135.0
...
437 178.0
438 104.0
439 132.0
440 220.0
441 57.0
Name: target, Length: 442, dtype: float64Обучение моделей и оценка полученных результатов
В случае классификации SVC справился лучше LinearSVC, сделав более гибкие границы разделения классов. Как можно заметить, решающие границы SVC получились гибкими, поскольку линейная граница решений в многомерном пространстве признаков будет соответствовать сложной нелинейной границе в исходном пространстве.
Однако такой подход не всегда работает лучше, что видно на примере регрессии: часто в данных с простой зависимостью линейное ядро демонстрирует лучшие результаты.
LinearSVC
linear_svc = LinearSVM(random_state=0)
linear_svc.fit(X1_train, y1_train)
linear_svc_pred_res = linear_svc.predict(X1_test)
linear_svc_accuracy = accuracy_score(y1_test, linear_svc_pred_res)
print(f'LinearSVC accuracy: {linear_svc_accuracy:}')
print(linear_svc_pred_res)
LinearSVC accuracy: 0.9210526315789473
[2 1 0 2 0 2 0 1 1 1 2 1 1 1 1 0 1 1 0 0 2 2 0 0 2 0 0 1 1 0 2 2 0 2 2 1 0
2]LinearSVC (scikit-learn)
sk_linear_svc = LinearSVC(loss='squared_hinge', max_iter=10000, random_state=0)
sk_linear_svc.fit(X1_train, y1_train)
sk_linear_svc_pred_res = sk_linear_svc.predict(X1_test)
sk_linear_svc_accuracy = accuracy_score(y1_test, sk_linear_svc_pred_res)
print(f'sk LinearSVC accuracy: {sk_linear_svc_accuracy:}')
print(sk_linear_svc_pred_res)
feature_indexes = [2, 3]
title1 = 'LinearSVC surface'
decision_boundary_plot(X1, y1, X1_train, y1_train, sk_linear_svc, feature_indexes, title1)
sk LinearSVC accuracy: 0.9210526315789473
[2 1 0 2 0 2 0 1 1 1 2 1 1 1 1 0 1 1 0 0 2 2 0 0 2 0 0 1 1 0 2 2 0 2 2 1 0
2]
SVC
svc = SVM(random_state=0, gamma='auto')
svc.fit(X1_train, y1_train)
svc_pred_res = svc.predict(X1_test)
svc_accuracy = accuracy_score(y1_test, svc_pred_res)
print(f'SVC accuracy: {svc_accuracy:}')
print(svc_pred_res)
SVC accuracy: 0.9736842105263158
[2 1 0 2 0 2 0 1 1 1 2 1 1 1 1 0 1 1 0 0 2 1 0 0 2 0 0 1 1 0 2 1 0 2 2 1 0
2]SVC (scikit-learn)
sk_svc = SVC(random_state=0, gamma='auto')
sk_svc.fit(X1_train, y1_train)
sk_svc_pred_res = sk_svc.predict(X1_test)
sk_svc_accuracy = accuracy_score(y1_test, sk_svc_pred_res)
print(f'sk SVC accuracy: {sk_svc_accuracy:}')
print(sk_svc_pred_res)
feature_indexes = [2, 3]
title2 = 'SVC surface'
decision_boundary_plot(X1, y1, X1_train, y1_train, sk_svc, feature_indexes, title2)
sk SVC accuracy: 0.9736842105263158
[2 1 0 2 0 2 0 1 1 1 2 1 1 1 1 0 1 1 0 0 2 1 0 0 2 0 0 1 1 0 2 1 0 2 2 1 0
2]
LinearSVR
linear_svr = LinearSVM(regression=True)
linear_svr.fit(X2_train, y2_train)
linear_svr_pred_res = linear_svr.predict(X2_test)
linear_svr_r2 = r2_score(y2_test, linear_svr_pred_res)
print(f'LinearSVR r2 score: {linear_svr_r2:}')
print(linear_svr_pred_res)
LinearSVR r2 score: 0.3792357370266678
[216.15968628 220.4481875 165.81989913 123.24660088 162.79339624
219.32628582 114.40328867 187.29239041 135.60608051 192.94216428
142.8356438 186.26887666 115.93676843 92.65131502 237.37770913
105.70347983 140.17045763 78.03390184 93.19336622 213.55077346
172.96582698 141.23351563 160.93321605 136.06861865 189.99746346
162.00412166 119.88834206 95.16558303 169.4791898 167.9510029
178.92773537 94.54901318 131.32930116 143.22717983 158.62314035
179.63207827 161.26232493 184.99305841 137.0911429 190.80874425
97.79122811 174.20746847 149.93081547 163.6511185 186.25250505
89.10531469 134.71035596 137.85610675 143.47793077 213.7920584
154.13931085 96.48578013 152.68919476 164.92850238 204.49516212
184.36868908 186.98158124 104.04646649 155.49588864 175.27621381
180.18811448 150.78618876 162.95426399 136.68414224 221.99330585
141.62183394 91.8349318 225.76370605 194.54965172 69.11345544
92.30405285 151.11667643 118.33817248 133.31474617 136.09121693
187.03275101 135.91418347 203.47303573 220.93494444 180.79064789
153.63359556 202.03121138 85.14842597 208.72273567 91.56979646
107.38020014 130.37078711 184.64399992 135.46766588 160.00350266
90.34899353 133.82900713 91.48257892 159.99266924 128.72744725
113.3641814 212.27373852 201.97525592 141.00148555 165.9290978
178.10808713 91.31945385 201.40199857 116.11341335 205.99603552
149.74428959 212.73484188 241.66640456 118.74948785 128.32248729
186.72222586]LinearSVR (scikit-learn)
sk_linear_svr = LinearSVR(loss='squared_epsilon_insensitive')
sk_linear_svr.fit(X2_train, y2_train)
sk_linear_svr_pred_res = sk_linear_svr.predict(X2_test)
sk_linear_svr_r2 = r2_score(y2_test, sk_linear_svr_pred_res)
print(f'sk LinearSVR R2 score: {sk_linear_svr_r2:}')
print(sk_linear_svr_pred_res)
sk LinearSVR R2 score: 0.37814542044497423
[215.54802943 220.69479521 163.72321514 125.35050039 168.23663006
222.87285934 117.76887939 183.439543 143.23792374 199.25861483
149.2464745 180.13546176 117.73284104 98.8129158 229.40677283
107.70075384 144.10708869 83.42833432 101.75722386 207.55264272
177.38566123 146.60127268 159.10274119 144.47851976 188.12741871
161.72800999 122.19555137 98.38934168 172.04469244 163.88747259
174.31869231 98.56101933 137.43514957 143.99818253 152.57005935
180.16575707 160.23942338 181.13802512 137.10299603 190.01855923
99.30200726 168.53506831 147.88091211 166.46196854 180.1601789
91.81189072 137.23909085 140.51020744 137.65220301 212.07954464
154.84803714 97.88215713 154.47755522 160.16521948 206.99600783
176.91673261 183.28777653 113.64466494 148.4110365 170.98296686
185.33374519 155.94941503 161.03649538 131.05262642 225.54785872
145.68037375 95.41892062 217.82197857 191.37652659 70.60017863
96.29414312 144.83768093 117.20983217 138.05827775 137.59789698
182.48375573 127.73687759 196.85281425 212.96526525 179.20675501
151.86717758 197.64279852 84.30187965 201.50000094 92.92382878
108.05315903 137.05696185 182.37076863 136.21049311 155.56310123
98.99174929 132.35640936 95.05326284 155.95524466 129.92134192
115.17532067 211.30425492 202.94673641 139.72699584 163.73270376
178.32978006 102.9526864 198.70259669 111.69518298 202.22368578
140.46518594 208.80233486 238.65552407 122.58886831 126.21856224
184.20163827]SVR
svr = SVM(regression=True)
svr.fit(X2_train, y2_train)
svr_pred_res = svr.predict(X2_test)
svc_r2 = r2_score(y2_test, svr_pred_res)
print(f'SVR r2 score: {svc_r2:}')
print(svr_pred_res)
SVR r2 score: 0.13842687260455933
[156.05494339 160.2561796 141.5352585 126.32530705 138.56287083
157.79461531 118.30051225 153.1126463 133.32684359 151.34517091
138.31021981 150.93156042 127.62035887 125.65861919 159.80948036
119.27243753 132.8868118 115.3503535 130.26443966 154.69113982
140.44764244 131.1864082 140.91091129 132.34658014 147.43835547
141.71095095 135.93497953 120.372006 141.90918325 145.01581208
147.05308508 115.34872572 128.98260578 139.39763958 141.37219221
149.93533907 144.21593809 147.00705167 128.79733929 154.94745068
122.27967665 145.73099063 138.72486465 142.87524309 149.4272714
119.3023132 129.77336124 128.95425751 135.62538778 154.4679459
137.44976849 114.591969 136.28102471 144.85720422 155.6502593
145.13807371 149.33504099 124.03772077 141.352508 147.84699051
148.25434815 133.39538615 143.03923607 131.48119845 154.73175072
132.94449565 118.51262122 149.10562494 147.22897373 130.57831287
116.89776562 139.90942034 125.511231 129.63878496 128.60606786
148.44879908 136.55938776 152.91463602 158.19071606 143.85231346
138.42641367 157.68211977 114.52184616 158.09339445 124.94398434
119.09508611 129.13111767 147.82792349 130.8519467 140.09356889
128.19793708 128.37423877 120.27278606 141.48530479 126.975866
118.21921492 156.0928224 150.71999387 132.67319998 142.29171129
149.6172972 127.40342245 152.28664393 129.07127394 158.18758274
139.54904295 151.99820233 154.43678117 124.87211774 126.92101192
152.02873799]SVR (scikit-learn)
sk_svr = SVR()
sk_svr.fit(X2_train, y2_train)
sk_svr_pred_res = sk_svr.predict(X2_test)
sk_svr_r2 = r2_score(y2_test, sk_svr_pred_res)
print(f'sk SVR r2 score: {sk_svr_r2:}')
print(sk_svr_pred_res)
sk SVR r2 score: 0.13842687260455933
[156.05494339 160.2561796 141.5352585 126.32530705 138.56287083
157.79461531 118.30051225 153.1126463 133.32684359 151.34517091
138.31021981 150.93156042 127.62035887 125.65861919 159.80948036
119.27243753 132.8868118 115.3503535 130.26443966 154.69113982
140.44764244 131.1864082 140.91091129 132.34658014 147.43835547
141.71095095 135.93497953 120.372006 141.90918325 145.01581208
147.05308508 115.34872572 128.98260578 139.39763958 141.37219221
149.93533907 144.21593809 147.00705167 128.79733929 154.94745068
122.27967665 145.73099063 138.72486465 142.87524309 149.4272714
119.3023132 129.77336124 128.95425751 135.62538778 154.4679459
137.44976849 114.591969 136.28102471 144.85720422 155.6502593
145.13807371 149.33504099 124.03772077 141.352508 147.84699051
148.25434815 133.39538615 143.03923607 131.48119845 154.73175072
132.94449565 118.51262122 149.10562494 147.22897373 130.57831287
116.89776562 139.90942034 125.511231 129.63878496 128.60606786
148.44879908 136.55938776 152.91463602 158.19071606 143.85231346
138.42641367 157.68211977 114.52184616 158.09339445 124.94398434
119.09508611 129.13111767 147.82792349 130.8519467 140.09356889
128.19793708 128.37423877 120.27278606 141.48530479 126.975866
118.21921492 156.0928224 150.71999387 132.67319998 142.29171129
149.6172972 127.40342245 152.28664393 129.07127394 158.18758274
139.54904295 151.99820233 154.43678117 124.87211774 126.92101192
152.02873799]Преимущества и недостатки метода опорных векторов
Преимущества:
высокая точность прогнозов;
может быть адаптирован к обнаружению аномалий в данных;
возможность обработки многомерных данных без их предварительного преобразования или понижения размерности.
Недостатки:
низкая скорость работы на данных большого размера;
из-за разделения данных на гиперплоскости может возникнуть чувствительность к шуму или нестабильная работа с сильно перекрывающимися классами в данных.
Дополнительные источники
Статьи:
«Statistical performance of Support Vector Machines», Gilles Blanchard, Olivier Bousquet and Pascal Massart;
«A review of optimization methodologies in Support Vector Machines», John Shawe-Taylor, Shiliang Sun;
«On the Algorithmic Implementation of Multiclass Kernel-based Vector Machines», Koby Crammer, Yoram Singer;
«LIBLINEAR: A library for large linear classification», Rong-En Fan, Kai-Wei Chang, Cho-Jui Hsieh, Xiang-Rui Wang, Chih-Jen Lin;
«LIBSVM: A Library for Support Vector Machines», Chih-Chung Chang and Chih-Jen Lin.
Документация:
Видео: один, два, три, четыре, пять, шесть, семь, восемь, девять, десять, одиннадцать.


vitosdrugak92
Спасибо за статью!
Я только начинаю свой путь в мир ML/DC, позволю себе задать глупый вопрос, а существует ли система или методика определения подходящего метода работы с вектораим на основе доступных данных для обучения ? Или это определяется эксперементально ?
egaoharu_kensei Автор
Если в двух словах, то всё начинается с разведочного анализа данных, поскольку он позволяет определить зависимость в данных и многое другое, что в конечном счёте поможет повлиять на выбор подходящего алгоритма. Другим важным фактором является поставленная задача, например, насколько важна скорость работы алгоритма и так далее.