Хабр, привет! В этой статье хочу поделиться с вами одной изящной задачей из нашего прошедшего квеста, которая, как мне кажется, заслуживает вашего внимания.
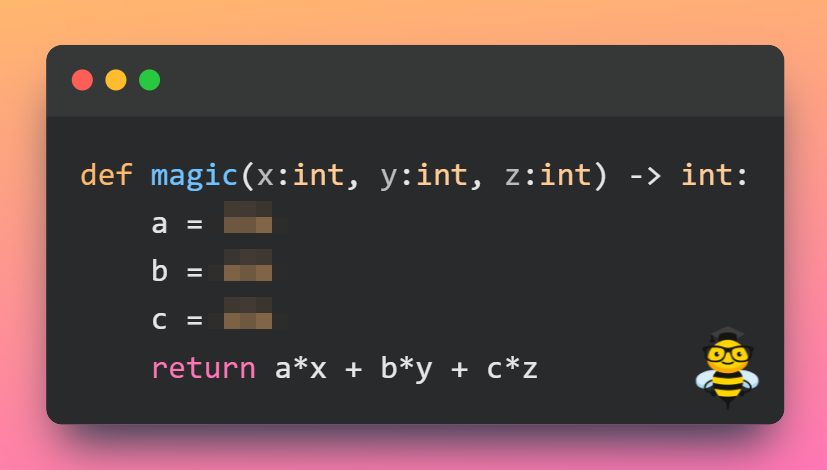
Имеется функция magic(), принимающая три целочисленных аргумента, в теле которой определены константы a, b, c, являющиеся натуральными числами. Требуется определить значения констант a, b и c за минимальное количество вызовов данной функции.
Три вызова функции и система уравнений
Первое, что может прийти в голову при виде такой задачи — это составление системы линейных уравнений:
вызывая функцию с аргументами
x = 1, y = 1, z = 1, мы получим значение выраженияa + b + cвызывая функцию с аргументами
x = 1, y = -1, z = 1, мы получим значение выраженияa - b + cвызывая функцию с аргументами
x = 1, y = 1, z = -1, мы получим значение выраженияa + b - c
Итого мы имеем систему трех линейных уравнений с тремя неизвестными a, b, c. Такая система имеет единственное решение, и его можно найти различными способами, например, методом подстановки.
Три вызова функции без системы уравнений
Поскольку по условию задачи аргументами функции magic() являются целые числа, то мы можем использовать значение 0. Это позволит нам избавиться от ненужных вычислений и сразу найти значения констант a, b и c:
вызывая функцию с аргументами
x = 1, y = 0, z = 0, мы получим значение константыaвызывая функцию с аргументами
x = 0, y = 1, z = 0, мы получим значение константыbвызывая функцию с аргументами
x = 0, y = 0, z = 1, мы получим значение константыc
Получили достаточно красивое решение: компактное и с минимумом вычислений. Однако и такое решение использует три вызова функции magic().
Можно ли сократить количество вызовов функции? Возможно ли решить задачу всего за два вызова функции magic()? Оказывается, можно — при условии, что константы a, b и c являются натуральными числами.
Напомним, что натуральные числа — это целые положительные числа, то есть числа 1, 2, 3, 4 и т. д. Множество натуральных чисел неограниченно сверху.
Два вызова функции
Возьмем произвольное число 8956734. Такое число можно разложить по степеням десяти (base = 10) в виде:
С таким же успехом мы можем разложить данное число по степеням ста (base = 100):
или даже по степеням тысячи (base = 1000):
Почему такое разложение работает? В первом случае число 10 больше, чем любая из цифр от 0 до 9, поэтому в сумме справа нигде не происходит наложения разрядов. Во втором случае число 100 больше, чем любое двухзначное число от 10 до 99. В третьем случае число 1000 больше, чем любое трехзначное число от 100 до 999.
Прежде чем переходить к самому решению, давайте вспомним, как мы можем посчитать количество цифр в произвольном натуральном числе. Для этого нам потребуется использовать десятичный логарифм (можно использовать и конвертацию в строку с последующим вызовом функции len(), но через логарифм получается интереснее).
Приведенный ниже код:
from math import log10
for num in [1, 13, 456, 1673, 56789, 258964, 1234567]:
digit_len = int(log10(num)) + 1
print(digit_len, 10**digit_len)выводит:
1 10
2 100
3 1000
4 10000
5 100000
6 1000000
7 10000000А теперь, собственно, решение задачи. ?
Делаем первый вызов функции magic() с аргументами x = 1, y = 1, z = 1, получаем значение суммы a + b + c, которое запишем в переменную total. Такое число total заведомо больше, чем каждое из чисел a, b и c. С помощью десятичного логарифма находим минимальную степень десяти, превышающую число total, которую запишем в переменную power.
Делаем второй вызов функции magic() с аргументами x = power**2, y = power, z = 1. В результате такого вызова мы получим число, которое и будет содержать все три константы a, b, c слева направо. Далее с помощью операторов // (целочисленное деление) и % (нахождение остатка) находим значения констант a, b, c по отдельности:
from math import log10
total = magic(1, 1, 1) # первый вызов функции
power = 10**(int(log10(total)) + 1)
numbers = magic(power**2, power, 1) # второй вызов функции
a, b, c = numbers // power**2, numbers % power**2 // power, numbers % power
print(a, b, c) Рассмотрим пример. Пусть функция magic() имеет вид:

Получаем:
total = 23 + 46 + 19 = 88
power = 10**2 = 100
numbers = 23*100**2 + 46*100 + 19 = 234619
a = 234619 // 100**2 = 23
b = 234619 % 100**2 // 100 = 46
c = 234619 % 100 = 19 Еще один пример. Пусть константы a, b и c состоят из разного количества цифр и функция magic() имеет вид:

Получаем:
total = 19567 + 4 + 231 = 19802
power = 10**5 = 100000
numbers = 19567*100000**2 + 4*100000 + 231 = 195670000400231
a = 195670000400231 // 100000**2 = 19567
b = 195670000400231 % 100000**2 // 100000 = 4
c = 195670000400231 % 100000 = 231Обратите внимание: в числе numbers могут быть "лишние" нули, но это нестрашно. В момент нахождения самих констант a, b и c незначащие ведущие нули пропадут.
Обобщения на большое количество неизвестных
Приведенное решение особенно красиво тем, что его можно масштабировать на любое количество неизвестных констант. В исходной задаче их всего три, но их может быть и больше, скажем, 5 или 10. Единственное, что надо будет поменять, так это код, извлекающий значения констант из итогового числа numbers: его легко обобщить и переписать в виде цикла while.
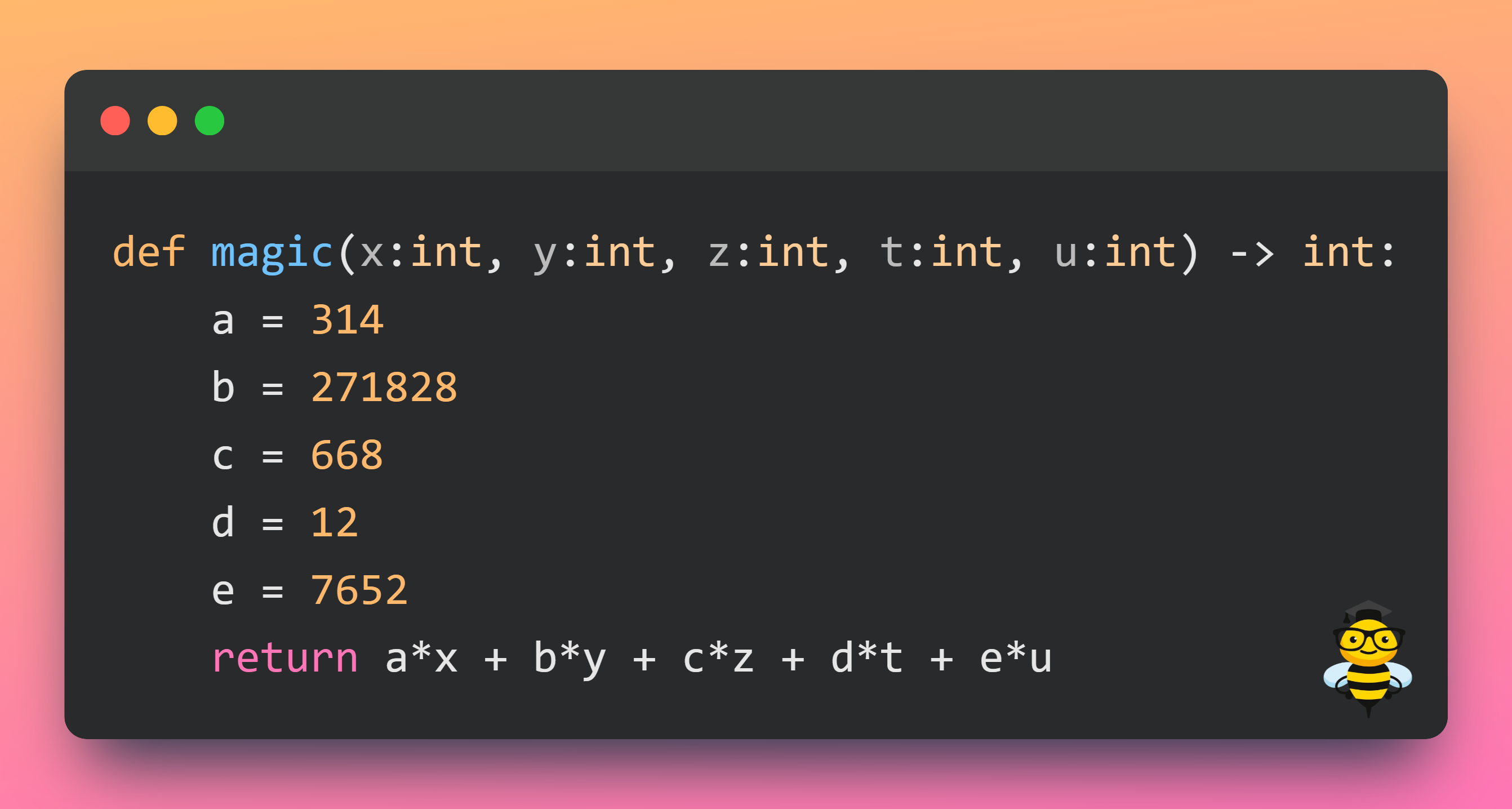
Рассмотрим пример функции magic() с пятью константами:
Приведенный ниже код:
from math import log10
total = magic(1, 1, 1, 1, 1) # первый вызов функции
power = 10**(int(log10(total)) + 1)
numbers = magic(power**4, power**3, power**2, power, 1) # второй вызов функции
constants = []
while numbers != 0:
constants.append(numbers % power)
numbers //= power
a, b, c, d, e = reversed(constants)
print(a, b, c, d, e)выводит значения всех пяти констант:
314 271828 668 12 7652Напоследок
В разобранном решении задачи с двумя вызовами функции magic() использовались степени десятки (base = 10) в качестве основания системы счисления. Обязательно ли их использовать? На самом деле нет! Мы сделали это исключительно для того, чтобы нам было чуток нагляднее, ведь мы привыкли иметь дело с десятичной системой счисления. В качестве основания системы счисления мы можем использовать значение total, равное сумме констант a, b и c, ведь оно заведомо больше, чем каждое из чисел a, b и c.
total = magic(1, 1, 1) # первый вызов функции
numbers = magic(total**2, total, 1) # второй вызов функции
a, b, c = numbers // total**2, numbers % total**2 // total, numbers % total
print(a, b, c) Пусть функция magic() имеет вид:
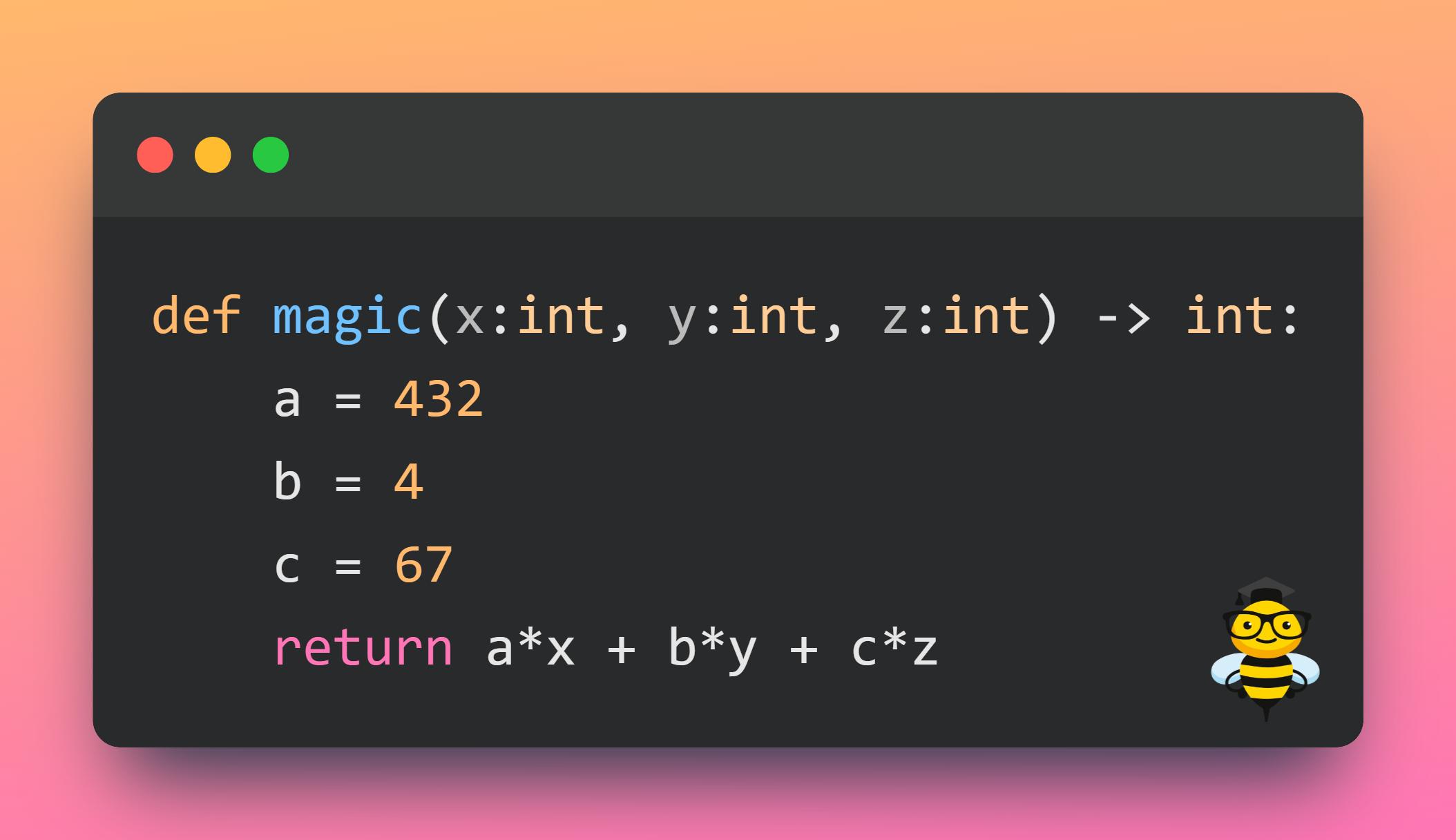
Получаем:
total = 432 + 4 + 67 = 503
numbers = 432*503**2 + 4*503 + 67 = 109301967
a = 109301967 // 503**2 = 432
b = 109301967 % 503**2 // 503 = 4
c = 109301967 % 503 = 67Напишите в комментариях, понравилась ли вам задача? Возможно, у вас есть другое решение, которое тоже использует всего два вызова функции. Поделитесь им! А может быть, вам удалось придумать решение задачи всего за один вызов? Делитесь им тоже!
Разбор остальных задач квеста будет опубликован чуть позже.
Присоединяйтесь к нашему телеграм-каналу, будет интересно и познавательно! ?
Комментарии (46)

longclaps
02.04.2024 06:48+46Задача мне не понравилась, из пальца высосана, а самодовольства море разливанное.
def magic(x: int, y: int, z: int) -> int: a = 1 b = 2 c = 3 return a * x + b * y + c * z s = magic("a", "b", "c") print(f'a={s.count("a")}, b={s.count("b")}, c={s.count("c")}')Без лоха и жизнь плоха.

sergio_nsk
02.04.2024 06:48+1А что,
(x: int, y: int, z: int) -> int:- задние типов аргументов и возвращаемого значения вообще ничего не ограничивает в Питоне?
CorwinH
02.04.2024 06:48+1вообще ничего не ограничивает в Питоне?
Ага. :)
Можно даже так написать:
def magic(x: print('hi'), y: int, z: int) -> int: a = 256 b = 512 c = 1024 return a * x + b * y + c * z

CorwinH
02.04.2024 06:48Ваш код не работает - падает с ошибкой. Точнее, работает или не работает в зависимости от значения констант.

Akina
02.04.2024 06:48А какие именно значения констант валят этот код? слишком большие?

CorwinH
02.04.2024 06:48слишком большие?
a = 10**19 для 64-битной системы. Для 32-битной 10**9, наверное.

CrazyOpossum
02.04.2024 06:4810**19не решится и методом из статьи. Там x =10**38и первое слагаемое переполнится в итоге.
upd: в питоне же длинная арифметика, да.

wataru
02.04.2024 06:48Это питон. Там длинная арифметика встроенная. Не упадет, если только там константы не по миллиону знаков.

asarkhipov
02.04.2024 06:48Можно вот так тогда:
def magic(x: int, y: int, z: int) -> int: a = 10000000000000000000000 b = 20000000000000000000000 c = 30000000000000000000000 return a * x + b * y + c * z class Num(int): mul: int | None def __new__(cls, x, *args, **kwargs): instance = int.__new__(cls, x, *args, **kwargs) instance.mul = None return instance def __rmul__(self, other) -> int: self.mul = other return super().__mul__(other) x = Num(1) y = Num(1) z = Num(1) magic(x, y, z) print(x.mul, y.mul, z.mul)

tguev Автор
02.04.2024 06:48Вы бы хотя бы условие задачи прочитали. Функция принимает целые числа в качестве аргументов, так что ваше решение в корне неверно.

NiPh
02.04.2024 06:48+8Это задача на программирование, с условием описанным конкретным кодом, на конкретном языке программирования.
Это решение запускается, и решает задачу, на мой читательский взгляд - с меньшим числом допущений, чем попытка угадать размерность константы, которая не указана в описании задачи или спецификаци функции.
svvaliv
02.04.2024 06:48+1Размерность констант может быть любой, в условии оговаривается то, что они явлются натуральными числами, то есть 1, 2, 3 и так далее. Решение, конечно, запускается, но оно вообще не оптимальное. Если константы будут достаточно большими, вычисление может занять очень много времени либо вообще выдаст MemoryError.

NiPh
02.04.2024 06:48+3Как программист я Вас очень хорошо понимаю. Но как олимпиадник - нет, потому что про время вычисления в условии не оговаривается. Понимаю это уже рефлекс из опыта разработки, но раз это ограничение не оговорено, и это сферическая задача в вакууме, а не часть продакшн модуля - его нет.

CorwinH
02.04.2024 06:48как олимпиадник - нет
Согласен. Задача сформулирована не корректно, с точки зрения соревнований/конкурса. Что-то (ограничения) приходится додумывать.

CrazyOpossum
02.04.2024 06:48+1Раньше в олимпиадном программировании всегда были ограничения и на память и на время. Решение прошло бы на хакерском квесте, но не на олимпиаде по математике или программированию.

NiPh
02.04.2024 06:48+1мы приходим к тому-же недостаточно описанному условию, при каком-то наборе тестов и констант прошло бы, при каком-то нет...

IkaR49
02.04.2024 06:48+9В условии не говорится, что они являются натуральными. Это дополнительное ограничение вводится, когда хочется притянуть за уши возможность решения с двумя вызовами:
Оказывается, можно — при условии, что константы
a, bиcявляются натуральными числами.Поэтому таким же образом, @longclaps может сказать: "Оказывается можно и за один - при условии, что константы в диапазоне от
0до10**19".

wataru
02.04.2024 06:48+7Нет, это решение отлично работет в питоне. Ваше решение тоже основано на тонкостях работы питона. Конкретно, на том, что там встроенная длинная арифметика. Если бы это был какой-нибудь C++ с 32-битными int-ами, то удачи вам получить назад число из 27 цифр.

alexejisma
02.04.2024 06:48+1Можно строки заменить на векторы: x = (1, 0, 0), y = (0, 1, 0), z = (0, 0, 1). Либо самому написать простенький класс, либо, например, воспользоваться numpy.

iqu
02.04.2024 06:48Ну это вообще на решение не тенет. А если у вас "черный ящик" с проверкой типов переданных аргументов?

andi123
02.04.2024 06:48Некоторое размышление сразу привели к тому, что нужно как-то разделить числа на разные интервалы порядков, не было только понятно как это сделать, без неоднозначности. А вот использование суммы неизвестных и исходя из этого использовать степени, вот это как раз любопытно, хотя после того как узнал, становится практически очевидным.
Самое забавное, что иногда такие задачи приходится решать. Но там есть известные ограничения на максимальное значение элементов.

CorwinH
02.04.2024 06:48+4после того как узнал, становится практически очевидным.
ИМХО это признак хорошей задачи.

winmasta
02.04.2024 06:48+2Если прочитать условие задачи НЕ смотря на картинку, то не понятно что возвращает функция. Вот так у нас и пишут документацию )

ti_zh_vrach
02.04.2024 06:48+140 вызовов:
from inspect import getsource def magic(x: int, y: int, z: int) -> int: a = 256 b = 512 c = 1024 return a * x + b * y + c * z print(getsource(magic))
CorwinH
02.04.2024 06:48+2Не хватает кода для разбора (парсинга) кода функции, чтобы определить значения констант. :)

ti_zh_vrach
02.04.2024 06:48+1Допустим, так:
from inspect import getsource def magic(x: int, y: int, z: int) -> int: a = 256 b = 512 c = 1024 return a * x + b * y + c * z def parse_var_vals(source_code: str) -> None: code_fragments = source_code.split(' ') func_vars = [fragment.strip() for fragment in code_fragments if ' = ' in fragment] vars_mapping = dict([var.split(' = ') for var in func_vars]) print(', '.join(func_vars)) print(vars_mapping) if __name__ == '__main__': parse_var_vals(getsource(magic))

Akina
02.04.2024 06:48+1С помощью десятичного логарифма находим минимальную степень десяти, превышающую число
total, которую запишем в переменнуюpowerНепонятно, почему бы не воспользоваться тривиальным
power = 1 + len(str(total))А если не нравится, что для точных степеней десятки оно даст больше, чем нужно - ну можно отнять единичку.


zartdinov
Вроде уравнение плоскости, которая проходит через центр координат, то есть нужны 2 любые точки чтобы однозначно определить все углы наклона.
tguev Автор
Некоторые участники квеста пытались использовать эту схожесть))
zartdinov
Я к тому, что в этой задаче в теории можно пару раз случайно вызвать функцию, не придумывая специальные значения и алгоритмы, только лень решать.
P.S. Я не прав (алгебраически и геометрически нужно вроде три случайных вызова).
CorwinH
Не совсем случайных. Нужно ещё чтобы матрица получилась невырожденной (строки/столбцы были линейно независимы).
wataru
Да, вот только вам надо эти точки угадать. Просто передав какую-то точку вы получите расстояние до плоскости (растянутое в константу раз). И просто по двум точкам вы однозначно плоскость не найдете.