В этой заметке я хочу разобрать несколько «парадоксов» в данных, о которых полезно знать как начинающему аналитику данных, так и любому человеку, кто не хочет быть введенным в заблуждение некорректными статистическими выводами.

За рассматриваемыми примерами не кроется сложной математики помимо базовых свойств выборки (таких, как среднее арифметическое и дисперсия), зато такие кейсы могут встретиться и на собеседовании, и в жизни.

«Новозеландцы, эмигрирующие в Австралию, повышают IQ обеих стран»

Эту цитату приписывают сэру Роберту Малдуну, премьер-министру Новой Зеландии. А может ли такое быть с точки зрения математики?

Итак, феноменом Уилла Роджерса называют кажущийся парадокс, заключающийся в том, что перемещение (численного) элемента из одного множества в другое может увеличить среднее значение обоих множеств. Начнем с очевидного примера: рассмотрим множества и . У среднее арифметическое элементов составляет 1, а у среднее арифметическое элементов составляет 550. Если взять число 100 и переместить его из второго множества в первое, то получатся множества со средним арифметическим 25.75 > 1 и со средним арифметическим 1000 > 550.

Тем не менее, совсем не обязательно, чтобы множества располагались так далеко друг от друга на числовой прямой, и не обязательно, чтобы перемещаемый элемент был минимальным во втором множестве и/или стал максимальным в первом.

Например, пусть . Среднее элементов множества составляет 5, а элементов множества — 7. Теперь переместим 6 из второго множества в первое, и получим множества со средним значением 5.1(6) и со средним значением 7.(3).

На самом деле такое увеличение обоих средних происходит при следующих условиях:

• перемещаемый элемент строго меньше среднего значения элементов второго множества до его удаления;

• перемещаемый элемент строго больше среднего значения первого множества до его добавления;

• как следствие, изначально среднее значение элементов первого множества (куда перемещают) должно быть строго меньше, чем у второго (откуда перемещают).

Вывод: подобная ситуация может встретиться в различных областях. Например, при улучшении диагностики заболеваний на ранней стадии ожидаемая продолжительность жизни среди здоровых и среди больных может увеличиться в одной и той же выборке, если некоторые из «здоровых» (а на самом деле плохо обследованных) перейдут в категорию «больных», и многие из них успешно вылечатся благодаря раннему выявлению болезни.

И да, внимательный читатель скажет, что никакого парадокса тут нет, и будет абсолютно прав. Это явление звучит немного контринтуитивно на словах, но примеры выше делают его очевидным.

Парадокс Симпсона

Представьте, что вы работаете в фирме, которая продает два типа продуктов, допустим, сепульки и бирюльки. (Допустим для простоты модели, что сепульки и бирюльки всегда учитываются в чеках по отдельности.) Утром к вам в кабинет забегает радостный стажёр-аналитик и сообщает, что за последний месяц средний чек в категории сепулек вырос на 5%, средний чек в категории бирюлек — на 7%. Общий средний чек он не проверял, но логично предположить, что он тоже вырос на некоторую величину в интервале между 5 и 7 процентов. Что могло пойти не так?

Вы открываете систему аналитики, смотрите подробнее и понимаете, что общий средний чек фирмы уменьшился, хотя цены на товары не менялись (то есть средний чек пропорционален количеству товаров в чеке), и скидок не было. Добавим в нашу оптимистичную таблицу дополнительные данные, без которых нельзя вычислить общий средний чек:

Средний чек в марте вычислен так: .

Вывод: не стоит делать выводы по отдельным показателям, если ключевую метрику задают не только они (в данном случае стажёр не учел, что в среднем чеке по всем покупкам категории фактически взвешиваются пропорционально доле покупок в них). Понимание парадокса Симпсона может уберечь от неверных выводов в том числе и при AB-тестировании.

Квартет Энскомба

А теперь история о том, почему визуализация данных бывает буквально необходима. Представьте, что вам рассказывают о четырёх множествах точек , про которые известно следующее: среднее значение переменной , дисперсия переменной , среднее значение переменной , дисперсия переменной и корреляция между переменными у них совпадают* для каждого из множеств. А также совпадают* коэффициенты, задающие прямую линейной регрессии.

^{*с точностью до двух-трёх знаков после запятой}

Казалось бы, выборки должны быть очень похожи между собой. Но здесь подвох кроется в том, что по умолчанию многие представляют себе что-то вроде нормального распределения (или другой из основных типов), хотя об этом изначально ничего не сказано. Воспользуемся датасетом из библиотеки seaborn и визуализируем эти данные:

import seaborn as sns
sns.set_theme(style="ticks")
# Load the example dataset for Anscombe's quartet
df = sns.load_dataset("anscombe")

# Show the results of a linear regression within each dataset
sns.lmplot(
    data=df, x="x", y="y", col="dataset", hue="dataset",
    col_wrap=2, palette="muted", ci=None,
    height=4, scatter_kws={"s": 50, "alpha": 1}
)

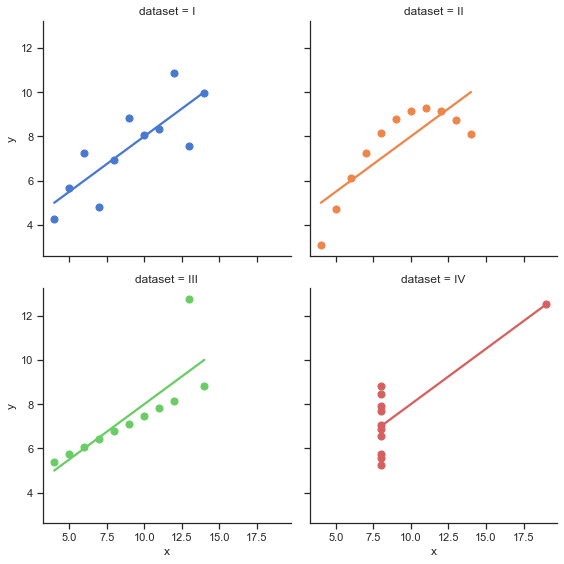
Посчитаем характеристики этих наборов точек:

mean_1 = df[df["dataset"] == "I"].mean()
mean_2 = df[df["dataset"] == "II"].mean()
mean_3 = df[df["dataset"] == "III"].mean()
mean_4 = df[df["dataset"] == "IV"].mean()
mean_1, mean_2, mean_3, mean_4

Этот код для подсчета средних по координатам и выводит следующий результат:

(x    9.000000
 y    7.500909
 dtype: float64,
 x    9.000000
 y    7.500909
 dtype: float64,
 x    9.0
 y    7.5
 dtype: float64,
 x    9.000000
 y    7.500909
 dtype: float64)

Код для остальных характеристик кладу под кат, чтобы не делать статью слишком длинной:

std_1 = df[df["dataset"] == "I"].std()
std_2 = df[df["dataset"] == "II"].std()
std_3 = df[df["dataset"] == "III"].std()
std_4 = df[df["dataset"] == "IV"].std()
std_1, std_2, std_3, std_4

(x    3.316625
 y    2.031568
 dtype: float64,
 x    3.316625
 y    2.031657
 dtype: float64,
 x    3.316625
 y    2.030424
 dtype: float64,
 x    3.316625
 y    2.030579
 dtype: float64)

import numpy as np

corr_1 = np.corrcoef(df[df["dataset"] == "I"]["x"], df[df["dataset"] == "I"]["y"])[0, 1]
corr_2 = np.corrcoef(df[df["dataset"] == "II"]["x"], df[df["dataset"] == "II"]["y"])[0, 1]
corr_3 = np.corrcoef(df[df["dataset"] == "III"]["x"], df[df["dataset"] == "III"]["y"])[0, 1]
corr_4 = np.corrcoef(df[df["dataset"] == "IV"]["x"], df[df["dataset"] == "IV"]["y"])[0, 1]
corr_1, corr_2, corr_3, corr_4

(0.81642051634484, 0.8162365060002428, 0.8162867394895984, 0.8165214368885028)

k1, b1 = np.polyfit(df[df["dataset"] == "I"]["x"], df[df["dataset"] == "I"]["y"], 1)
k2, b2 = np.polyfit(df[df["dataset"] == "II"]["x"], df[df["dataset"] == "II"]["y"], 1)
k3, b3 = np.polyfit(df[df["dataset"] == "III"]["x"], df[df["dataset"] == "III"]["y"], 1)
k4, b4 = np.polyfit(df[df["dataset"] == "IV"]["x"], df[df["dataset"] == "IV"]["y"], 1)

k1, k2, k3, k4, b1, b2, b3, b4

(0.5000909090909095,
 0.5000000000000002,
 0.499727272727273,
 0.4999090909090908,
 3.0000909090909076,
 3.0009090909090905,
 3.0024545454545457,
 3.0017272727272712)

Вывод: иногда и взгляда на все основные статистики не будет достаточно, и тогда необходима визуализация. При этом зачастую даже самого простого scatter plot (графика с точками на плоскости) хватит, чтобы заметить различия в выборках.

The Datasaurus Dozen

Квартет Энскомба наглядно демонстрирует, почему визуализация данных важна, но подобрать 4 множества по 11 точек — ничего особенного, не так ли? Более интересным примером может быть «датазаврова дюжина», состоящая из 13 наборов точек, которые складываются в различные фигуры.

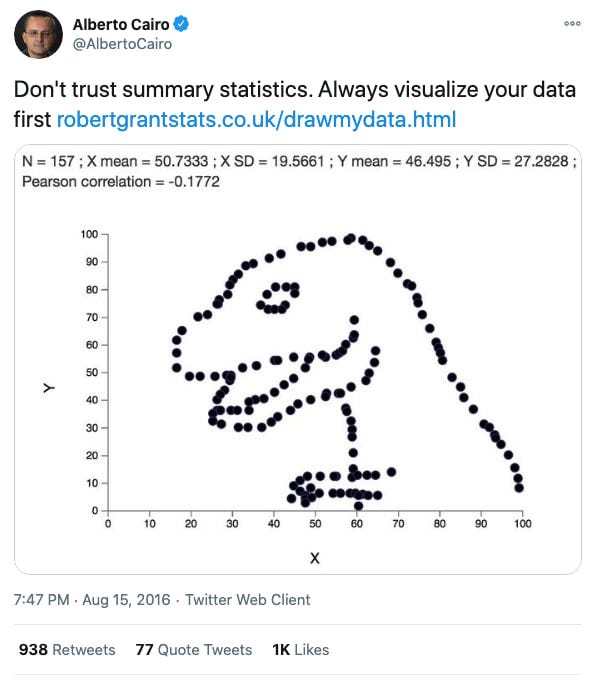
Подход авторов заключался в том, что изначально был взят «динозавр» из точек, а затем данные итеративно незначительно менялись так, чтобы значения средних, дисперсий и коэффициента корреляции оставались такими же с точностью до двух знаков после запятой, до тех пор, пока не получалась очередная фигура (овал, звезда и так далее). Для каждой из полученных фигур потребовалось около 200 тысяч итераций алгоритма.

Псевдокод алгоритма для генерации таких наборов точек имеет следующий вид:

current_ds ← initial_ds
for x iterations, do:
    test_ds ← perturb(current_ds, temp)
    if similar_enough(test_ds, initial_ds):
        current_ds ← test_ds

function perturb(ds, temp):
    loop:
        test ← move_random_points(ds)
        if fit(test) > fit(ds) or temp > random():
            return test

• initial_ds — изначальный набор точек

• current_ds — набор точек на данный момент

• fit() — функция, проверяющая, насколько набор точек на данный момент напоминает нужную фигуру

• similar_enough() — функция, проверяющая, что значения статистик достаточно близки

• move_random_points() — функция, случайным образом сдвигающая точки

Заключение

Все эти примеры подводят нас к важности применения разведочного анализа данных (exploratory data analysis) — это выражение обозначает подход к работе с данными через анализ всех основных показателей и (практически всегда) их визуализацию. Критический взгляд на выводы, сделанные по паре показателей — важная черта как аналитика данных, так и любого человека, который не хочет позволить себя обмануть.

Спасибо, что дочитали! Буду рада дополнениям и вопросам в комментариях.