Уважаемое сообщество,
с большим удовольствием я вступаю в ваши ряды, чтобы поделиться собственными разработками в области оптимизации, и для начала несколько слов о себе. Моим образованием является инженерное дело в области автоматизации производств, и параллельно на протяжении долгого времени я занимаюсь программированием и разработкой торговых стратегий. Мой язык общения с финансовыми рынками - MQL5.
Однако я всегда ощущал влечение к оптимизации. И вот, благодаря упорству и настойчивости, все же я смог адаптировать один из таких алгоритмов для торговли еще много лет назад :) Это было настоящим открытием для меня, и я был восхищен тем, как алгоритмы могут влиять на результаты в финансовой сфере.
Мои текущие исследования сосредоточены на метаэвристических популяционных алгоритмах оптимизации. Я прилагаю усилия для разработки собственных уникальных методов и каждый день погружаясь в этот творческий процесс. Давайте вместе разделим наши идеи, обсудим новые тенденции и воплотим в жизнь самые смелые проекты. Ведь именно объединение интеллектов и творческих усилий позволяет нам достичь великих результатов. Поехали…
Многопопуляционные и многороевые алгоритмы оптимизации представляют собой мощные инструменты, основанные на использовании нескольких независимых популяций для решения задач оптимизации. Эти алгоритмы работают параллельно, обмениваясь информацией об оптимальных решениях и исследуя разные области пространства параметров.
В данной статье рассмотрим многопопуляционный алгоритм эволюции социальных групп ESG (Evolution of Social Groups) собственной разработки, который был написан мной буквально на одном дыхании за пару часов, и изучим принципы его работы.
Многопопуляционные алгоритмы оптимизации представляют собой методы, в которых несколько независимых групп агентов работают над решением одной и той же задачи оптимизации. Каждая группа агентов функционирует независимо от остальных групп и проводит свои поисковые операции в пространстве параметров. Такой подход позволяет исследовать различные области пространства одновременно и находить оптимальные решения. В отличие от «моно» - популяционных алгоритмов, где все агенты работают в одной популяции, многопопуляционные алгоритмы предоставляют большую гибкость.
Многопопуляционные алгоритмы оптимизации имеют общие следующие принципы:
Популяции (группы). Группы агентов сотрудничают и обмениваются опытом о лучших решениях.
Коллективное движение. Частицы внутри групп совместно перемещаются в пространстве параметров.
Локальный и глобальный опыт. Группы сохраняют лучшие решения (локальные внутри группы и глобальные).
Эволюция и обмен опытом. Алгоритм проходит через итерации, обновляя группы согласно улучшенным решениям и обмениваясь опытом.
Рассмотрим особенности поисковой стратегии ESG. В группе частиц, называемой "социальной группой", существует определенная центральная модель поведения. Частицы могут отклоняться от центра согласно закону распределения. Более приспособленная модель поведения становится новым центром группы, таким образом, группа перемещается в поисках стабильной модели поведения. Это многопопуляционный алгоритм, в котором моделируется поведение членов группы на низком уровне и глобальное поведение групп на высоком уровне.
Группы могут останавливаться в развитии и застревать в локальных экстремумах, этой проблемой страдают большинство метаэвристических алгоритмов. Для избежания застревания используется тактика "расширения сферы влияния социальной группы". Границы группы расширяются, чтобы открыть новые области поиска и разнообразить популяцию членов в группе, что помогает избежать застревания в локальных экстремумах. При нахождении нового решения границы сокращаются, побуждая группу к уточнению решения.
Однако простое расширение зоны влияния при фиксированном текущем положении центра группы может быть неэффективными. В таких случаях возникает необходимость передвинуть центр группы в новое положение. Для реализации стимула к перемещению центра групп достаточно обменяться успешным опытом между группами, поэтому частицы способны заимствовать идеи у центров других групп. Влияние новых идей может привести группу как к новым открытиям и улучшению положения в пространстве решений, так и ухудшить. Модель поведения социальных групп представлена на рисунке.
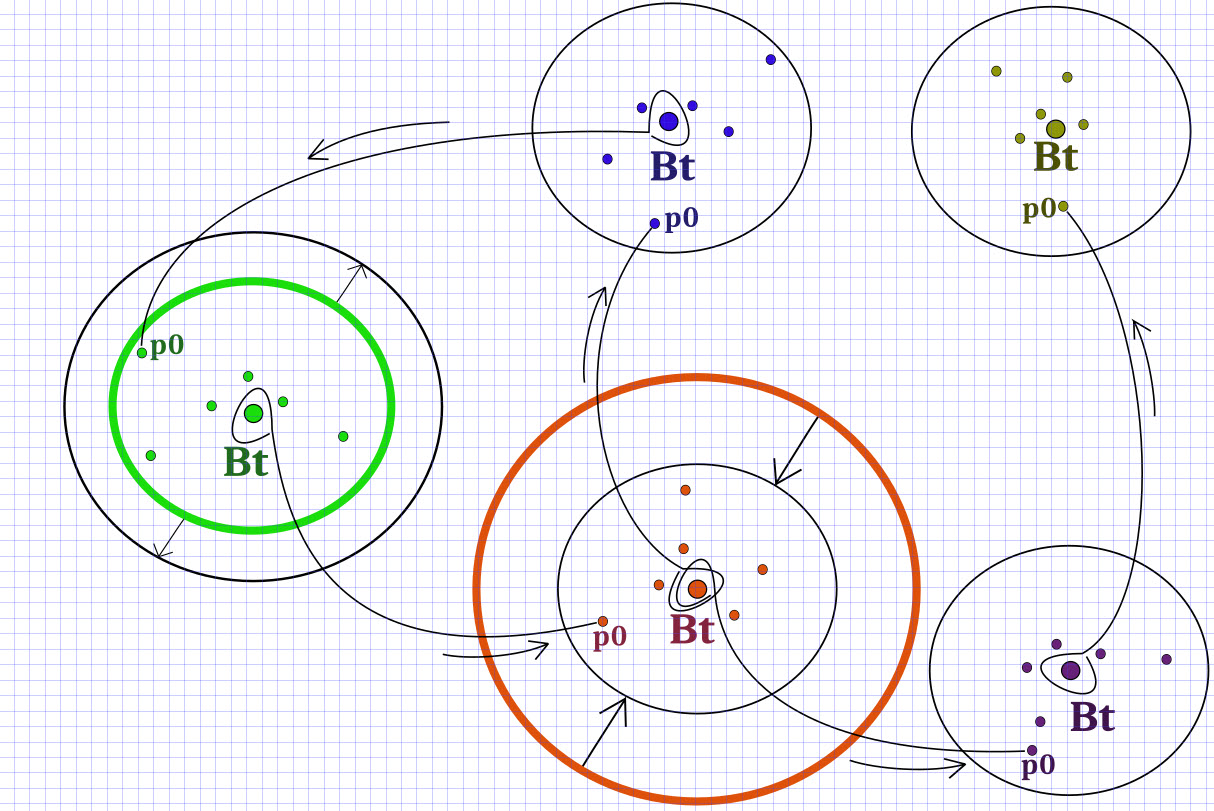
На схеме выше расширение группы происходит в случае отсутствия прогресса, сужение - в случае улучшения решения, заимствование "лучших идей" (координат) от соседних групп "Bt" (best of team) частицами "p0".
Псевдокод алгоритма ESG можно представить в следующем виде:
Поместить случайным образом центры групп в пространстве поиска.
Разместить частицы групп вокруг соответствующих центров с заданным распределением.
Рассчитать значения приспособленности частиц.
Обновить после п.3 глобальное решение.
Обновить затем центр каждой группы.
Расширить границы групп в случае отсутствия улучшения положения центра и уменьшить, если удалось улучшить положение.
Разместить частицы групп вокруг соответствующих центров с заданным распределением.
Добавить информацию из центров "чужих групп" в одну частицу каждой группы (частица получает набор координат из чужих групп, выбранных случайным образом).
Рассчитать значения фитнес-функции частиц.
Повторить с п.4 до выполнения критерия останова.
Реализация алгоритма ESG на языке C#
Алгоритм "Evolution of Social Groups" (ESG) на C# включает в себя следующие основные шаги:
1. "Инициализация": Создаются структуры "S_Group" и "S_Agent" для представления групп и агентов соответственно. Класс "C_AO_ESG" инициализирует эти структуры и параметры алгоритма.
2. "Цикл оптимизации": В цикле, который продолжается до выполнения критерия остановки, выполняются следующие шаги:
"Вычисление фитнес-функции": Для каждого агента вычисляется значение фитнес-функции.
"Обновление групп": Группы обновляются на основе текущих позиций агентов.
"Обновление позиций": Позиции агентов обновляются в зависимости от их группы.
3. "Возврат лучшего решения": После завершения цикла оптимизации возвращается лучшее найденное решение.
Описание отдельных методов в коде алгоритма "Evolution of Social Groups" (ESG):
1. Init. Этот метод инициализирует параметры алгоритма и начальную популяцию. Он также разделяет популяцию на группы.
2. Moving. Метод отвечает за первоначальное размещение групп в пространстве поиска и агентов в группах.
3. Revision. Здесь обновляются позиции агентов, если не произошло улучшения, радиус группы увеличивается, наоборот- уменьшается. Этот метод так же пересматривает позиции агентов и обновляет лучшее найденное решение, если агент находится вне границ, его позиция корректируется.
4. SeInDiSp. Метод используется для обеспечения того, чтобы значение находилось в заданном диапазоне. Если значение выходит за границы диапазона, оно корректируется до ближайшей границы с соблюдением шага поиска.
5. RNDfromCI. Этот метод генерирует случайное число в заданном диапазоне.
6. Scale. Этот метод масштабирует входное значение из одного диапазона в другой.
7. PowerDistribution. Этот метод используется для генерации новых позиций агентов с использованием степенного распределения.
Ниже код метода Revision, а весь код на C# с примером использования можно найти здесь.
public void Revision()
{
for (int i = 0; i < popSize; i++)
{
if (a[i].f > fB)
{
fB = a[i].f;
Array.Copy(a[i].c, cB, a[i].c.Length);
}
}
int cnt = 0;
bool impr = false;
for (int s = 0; s < groups; s++)
{
impr = false;
for (int p = 0; p < gr[s].sSize; p++)
{
if (a[cnt].f > gr[s].fB)
{
gr[s].fB = a[cnt].f;
Array.Copy(a[cnt].c, gr[s].cB, a[cnt].c.Length);
impr = true;
}
cnt++;
}
if (!impr) gr[s].sRadius *= expansionRatio;
else gr[s].sRadius = groupRadius;
if (gr[s].sRadius > 0.5) gr[s].sRadius = 0.5;
}
double coordinate = 0.0;
double radius = 0.0;
double min = 0.0;
double max = 0.0;
cnt = 0;
for (int s = 0; s < groups; s++)
{
for (int p = 0; p < gr[s].sSize; p++)
{
for (int c = 0; c < coords; c++)
{
if (RNDfromCI(0.0, 1.0) < 1.0)
{
radius = (rangeMax[c] - rangeMin[c]) * gr[s].sRadius;
min = gr[s].cB[c] - radius;
max = gr[s].cB[c] + radius;
if (min < rangeMin[c]) min = rangeMin[c];
if (max > rangeMax[c]) max = rangeMax[c];
coordinate = PowerDistribution(gr[s].cB[c], min, max, power);
a[cnt].c[c] = SeInDiSp(coordinate, rangeMin[c], rangeMax[c], rangeStep[c]);
}
}
cnt++;
}
}
cnt = 0;
for (int s = 0; s < groups; s++)
{
for (int c = 0; c < coords; c++)
{
int posSw = (int)RNDfromCI(0, groups);
if (posSw >= groups) posSw = groups - 1;
a[cnt].c[c] = gr[posSw].cB[c];
}
cnt += gr[s].sSize;
}
}Кто дочитал до конца, тому будет интересно, что алгоритм тестируется на тестовой функции Растригина, причем в коде легко можно заменить функцию на любую другую при желании, она не является частью класса. Такая архитектура алгоритма позволяет реализовывать любые пользовательские приложения, где требуется оптимизация.
Выводы
Алгоритм "Evolution of Social Groups" (ESG) - это эффективный метод оптимизации, основанный на взаимодействии групп. Он адаптивен, разнообразен и способен находить оптимальные решения в различных задачах. ESG может быть применен в областях, где требуется оптимизация параметров, таких как машинное обучение, оптимальное управление и комбинаторная оптимизация.
Архитектура ESG позволяет легко внедрять различные методы оптимизации, объединяя их преимущества. ESG - это гибкое и самодостаточное решение для сложных задач.
Особенности алгоритма ESG:
Простая архитектура и высокая переносимость на другие языки программирования.
Высокая сходимость на сложных задачах.
Чрезвычайно быстрый алгоритм с низкими вычислительными требованиями.
Комментарии (4)

ProtoPlazmoid Автор
04.04.2024 13:18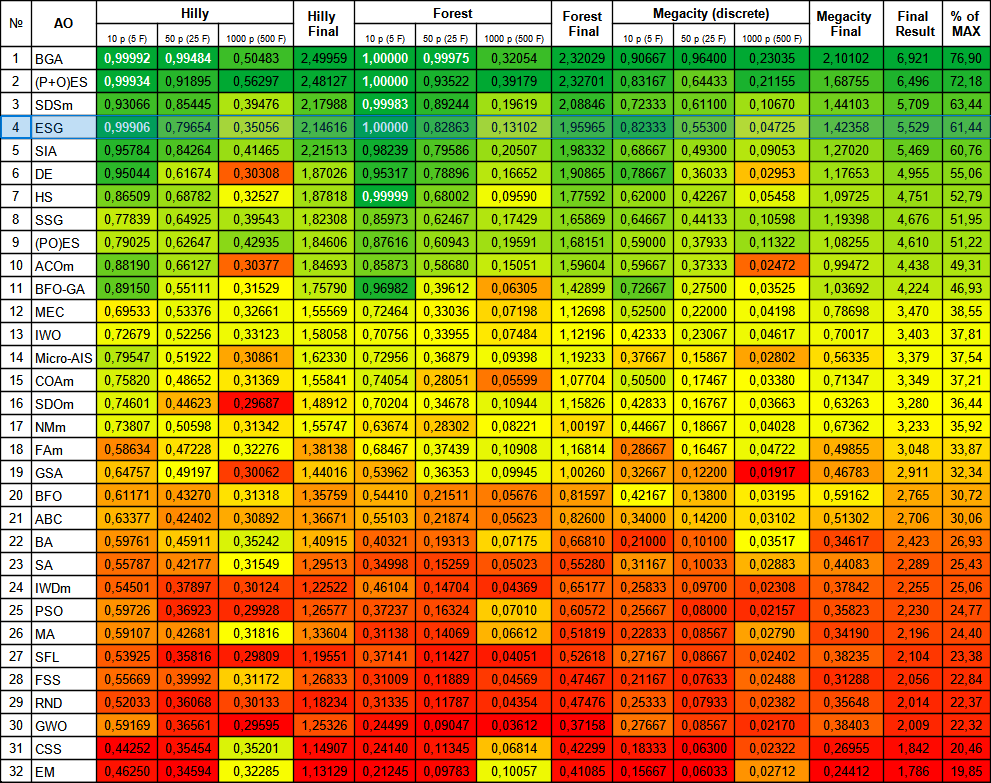
Рейтинговая таблица алгоритмов оптимизации. Это моя первая пробная статья-знакомство с хабром. Вот здесь результаты огромной исследовательской работы: https://www.mql5.com/ru/users/joo/publications. Цикл статей, посвященных популяционным алгоритмам оптимизации, в частности ESG: https://www.mql5.com/ru/articles/14136. В репозитарии github (https://github.com/JQSakaJoo/ESG) лежит полная версия алгоритма ESG на С#, абсолютно рабочая, код легкий и удобный, алгоритм быстрый и простой, тестовый пример работы с алгоритмом на функции Растригина (поиск максимума), пробуйте, пользуйтесь на здоровье ... пожалуйста, наверное Вы уже всё попробовали, какие у Вас результаты выдает алгоритм в зависимости от количества эпох? Кроме того, в исходнике есть ссылка на автора алгоритма, Вы смотрели? - или Вы только поверхностно прошлись, так сказать не углубляясь:)
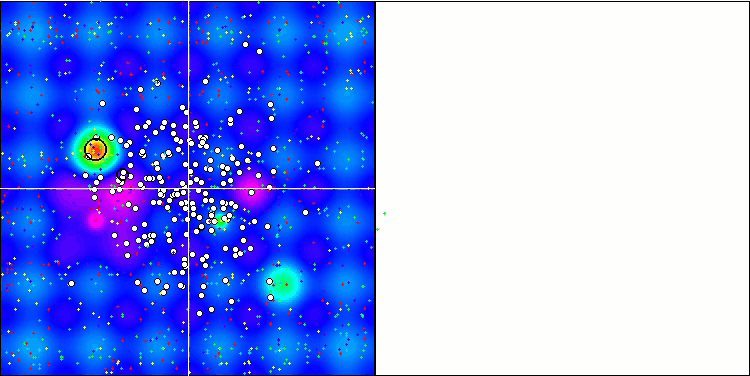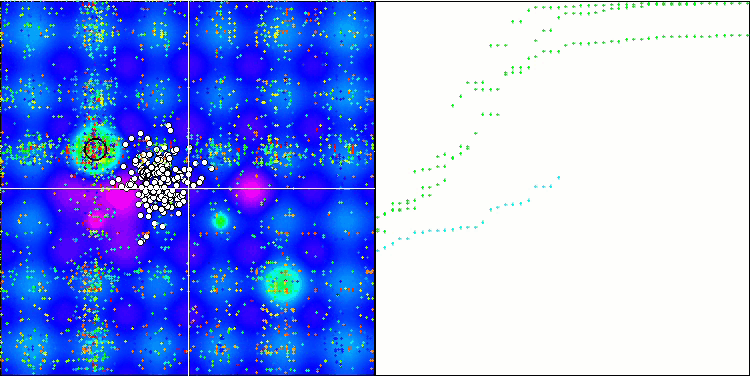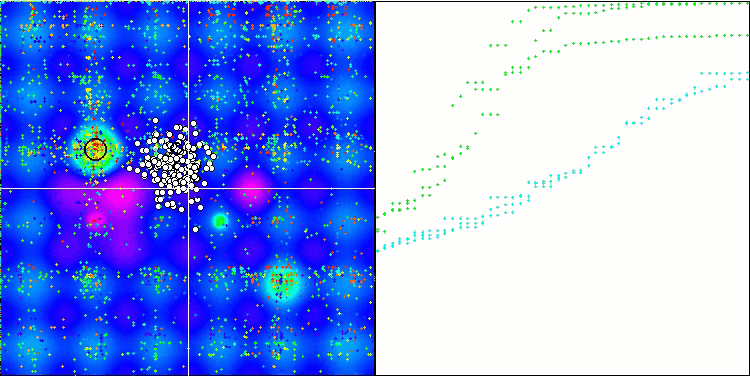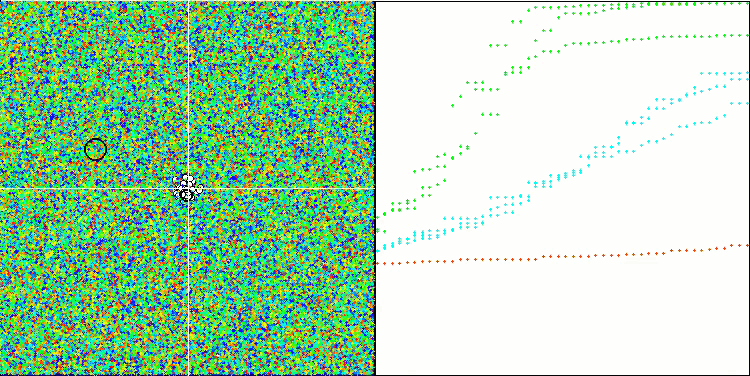
Работа ESG на тестовой функции Hilly с 10, 50 и 1000 оптимизируемых параметров (авторская тестовая функция, гораздо сложнее большинства известных стандартных тестовых функций, таких как Растригина, Экли, Розенброка, и др.).

sombik
04.04.2024 13:18+1Вы меня конечно извините, но я просто обожаю название переменных, особенно
gr,s,aи прочие. Сразу все понятно становится, и даже не нужно спрашивать, что и для чего предназначено.
(Сарказм)

VadimChes
04.04.2024 13:18+2Из чего следуют выводы об эффективности и сходимости? Для этого нужно было бы продемонстрировать сравнение с другими методами. Показалось, что статья какая-то поверхностная, картинка, общая идея и код одной функции, хотя все их можно на гитхабе увидеть... Как выбирать фитнесс функцию? Итого, много вопросов после прочтения и едиснтвенный вариант - смотреть полный код... Тогда статья вообще не имеет смысла. Разве что как реклама репозитория...



ProtoPlazmoid Автор
Ну, это, в основном, счётчики, а большинство переменных имеют осмысленные имена.