Пролог
В программировании часто возникает задача найти угол между векторами. Например пишите вы прошивку для PTZ камеры. У вас есть датчик текущего положения объектива. И есть желаемое направление положения объектива. Вам надо вычислить ошибку в градусах. Вам надо определить знак ошибки и решить в какую сторону надо поворачивать чтобы затратить минимальную энергию и время.
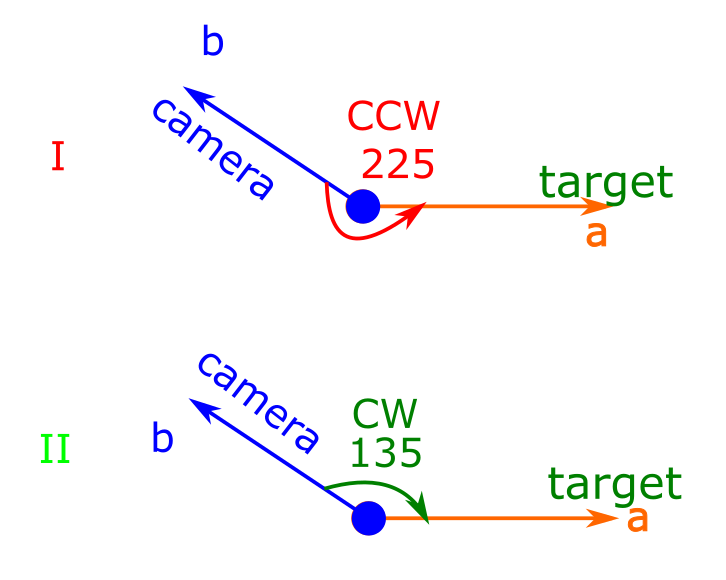
Чисто формально, между двумя векторами можно увидеть два угла: тот, что отсчитывается по часовой стрелке, и тот, что отсчитывается против часовой стрелки. В данном примере логично поворачивать камеру по часовой стрелке.
Теперь вместо PTZ камеры ставим радарную антенну и приходим к выводу, что надо решать ту же самую задачу: найти угол между векторами.
Потом в SDR обработке в цифровых PLL надо находить разность фаз между двумя комплексными числами (по сути- векторами).
Мне так часто приходилось решать задачу поиска угла между векторами, что я решил написать про это заметку.
Определения
Скаляр - число, которое не зависит от выбора системы координат. Скаляр всегда описывается одним числом
Вектор - это математический объект, который имеет величину и направление. Говоря по простому, вектор - это направленный отрезок. Пример вектора это стрелка компаса, или направление ветра в данной местности. Комплексное число a+j*b тоже можно рассматривать как вектор на плоскости.
Скалярное произведение векторов - это операция над двумя векторами, результатом которой является скаляр. Если угол между векторами прямой, то скалярное произведение равно 0.
Определитель - это скалярная величина. Используется при вычислении векторного произведения.
Векторное произведение - вектор, перпендикулярный обоим исходным векторам, длина которого численно равна площади параллелограмма, образованного исходными векторами, а выбор из двух направлений определяется так, чтобы тройка из по порядку стоящих в произведении векторов и получившегося вектора была правой
Постановка задачи.
Даны два вектора на плоскости Va=(xa,ya,0) и Vb=(xb,yb,0). Спрашивается найти угол между этими векторами в градусах (так привычнее). Также определить знак этого угла (+ или -). Разумеется, об углах между векторами имеет смысл говорить лишь для двух ненулевых векторов.
Очевидно, что этот угол между векторами может принимать значения от -180...0... 180 градусов. Или -pi ....pi радиан. Не больше ни меньше. К слову, угол между векторами 180 Deg и -180 Deg - это один и тот же угол.
Для начала, как обыкновенно, набросаем модульных тестов. Чтобы мы понимали, что мы делаем и для чего? Какой результат мы ожидаем и чего хотим? Всё это надо отразить в списке с модульными тестами. Только потом кидаться писать код. Это же очевидно.... Вот список этих тестов.
номер |
Вектор A |
Вектор B |
ожидаемый угол |
||
теста |
a_x |
a_y |
b_x |
b_y |
градусы |
1 |
1 |
0 |
0 |
1 |
+90 |
2 |
0 |
1 |
1 |
0 |
-90 |
3 |
0 |
0 |
0 |
0 |
Угол не определён. Может быть любой угол. |
4 |
1 |
1 |
1 |
1 |
0 |
5 |
1 |
0 |
-1 |
0 |
180 |
6 |
1 |
0 |
-1 |
-1 |
-135 |
7 |
1 |
0 |
-1 |
1 |
135 |
8 |
0 |
0 |
0 |
0 |
0 |
9 |
1 |
0 |
0 |
0 |
0 |
Решение
Для вычисления этого угла придется воспользоваться линейной алгеброй и аналитической геометрией. Классическим способом вычисления модуля угла между векторами является скалярное произведение. Об этом знает даже школьник.
Как известно угол между векторами показывает скалярное произведение. Даешь два вектора, получаешь число. По определению скалярное произведение равно произведению длин векторов на косинус угла между ними (скалярное произведение для двух векторов с координатами (a_x; a_y) и (b_x; b_y) вычисляется по формуле (1)
Как видно скалярное произведение максимально когда cos=1 то есть угол равен нулю. Одновременно скалярное произведение 0, когда векторы ортогональные (угол 90 градусов).
Из уравнения (1) можно выразить theta
Hidden text
\theta= arccos ( \frac{a_xb_x+a_y b_y }{\left |\overrightarrow{a} \right | \left |\overrightarrow{b} \right |}) \qquad \qquad \qquad (2)
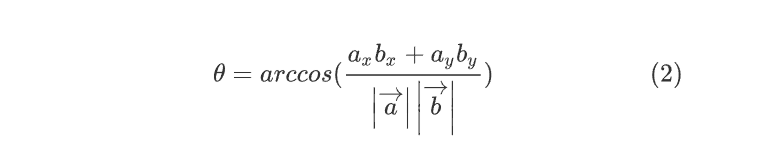
В знаменателе происходит перемножение длин векторов.
Но вот одна неприятность. Формула (2) выдает только модуль этого угла. А для всяческих систем автоматического управления, SDR обработки, нужен ещё и знак угла (+ или -) учитывая, что векторы образуют правую тройку. Да. Вот так..
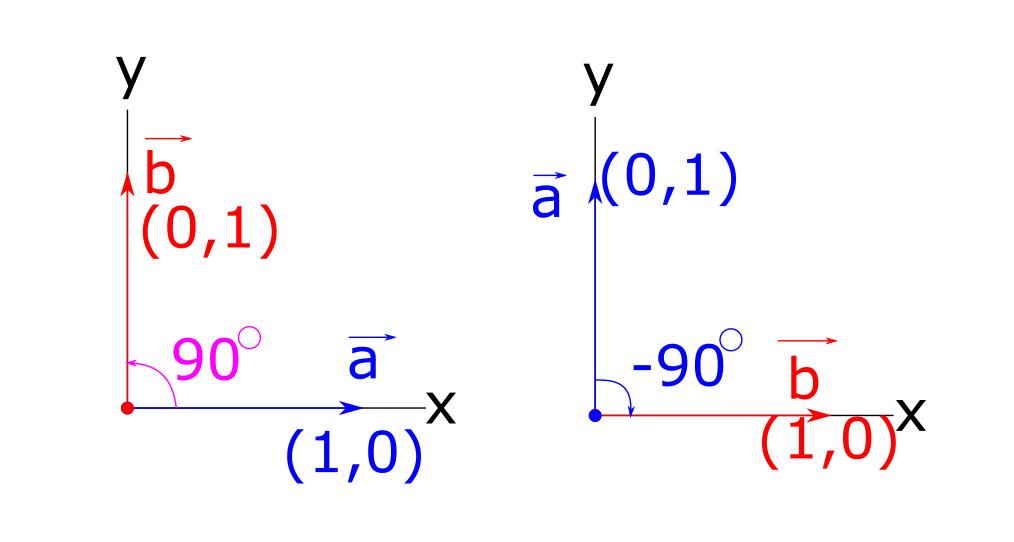
Вот тут, как раз, и начитается институтская математика: матрицы, определители, векторы и прочее. Знак нам определит уже векторное произведение. Идея очень проста. Мы вычислим векторное произведение [a,b] и посмотрим на знак z компоненты получившегося результата. По сути знак угла - это знак определителя для вектора k. Это и будет знак угла между векторами.
Получается, что финальная формула для угла между векторами кристаллизируется в такой вид
Громоздко? Да. Вот так... А Вы как хотели? Математика...
Программная часть
Любую математику лучше всего делать на Си. Тогда вы сможете запускать код на любой платформе. На разных микроконтроллерах, в Linux ядре, в User Spaсe и прочих программах.
typedef struct {
double dx;
double dy;
double dz;
} Vector_t;
bool is_double_equal_absolute(double d1, double d2, double precision) {
bool res = false;
qWord_t w1;
qWord_t w2;
w1.val = d1;
w2.val = d2;
if(w1.num == w2.num) {
res = true;
} else {
if(((d1 - precision) <= d2) && (d2 < (d1 + precision))) {
res = true;
} else {
res = false;
}
}
return res;
}
bool double_is_zero(double value) {
bool res = false;
res = is_double_equal_absolute(0.0, value, 0.000001);
return res;
}
double dot_product(const Vector_t*const v1, const Vector_t* const v2) {
double dot = 0.0;
dot = (v1->dx) * (v2->dx) + (v1->dy) * (v2->dy) + (v1->dz) * (v2->dz);
return dot;
}
double norm(const Vector_t* const Node) {
double norm=0.0;
if(Node) {
double argument=((Node->dx) * (Node->dx)) + ((Node->dy) * (Node->dy)) + ((Node->dz) * (Node->dz));
norm = sqrt(argument);
}
return norm;
}
double math_sign(double val) {
if (0.0 < val) {
return 1.0;
}
if (val < 0.0) {
return -1.0;
}
return 0.0;
}
/**/
double calc_angle_between_vectors_rad(
const Vector_t* const v1,
const Vector_t* const v2) {
LOG_DEBUG(MATH,"V1:%s",VectorToStr(v1));
LOG_DEBUG(MATH,"V2:%s",VectorToStr(v2));
double betta_rad = 0.0, norm1, norm2, absBetta_rad;
double dotPr;
Vector_t v3;
norm1 = norm(v1);
norm2 = norm(v2);
bool res1= double_is_zero( norm1);
bool res2= double_is_zero( norm2);
if (res1 || res2) {
return 0.0;
} else {
dotPr = dot_product(v1, v2);
absBetta_rad = acos(dotPr / (norm1 * norm2));
// scalar multiplication gives just module of the angle.
// vector multiplication gives the sign of the angle.
v3 = cross(v1, v2);
if ( double_is_zero(v3.dx) && double_is_zero(v3.dy) && double_is_zero(v3.dz)) {
betta_rad = absBetta_rad;
} else {
betta_rad = math_sign(v3.dz) * absBetta_rad;
}
}
LOG_DEBUG(MATH,"AbsTheta:%f rad,Theta:%f rad",absBetta_rad,betta_rad);
return betta_rad;
}
Как вариант можно еще вычислить угол между векторами если представить векторы как комплексные числа.
#include <complex.h>
const char* VectorToStr(const Vector_t* const Node){
static char text[80]="";
if(Node) {
strcpy(text,"");
snprintf(text,sizeof(text),"%s(dx:%f,",text,Node->dx);
snprintf(text,sizeof(text),"%sdy:%f,",text,Node->dy);
snprintf(text,sizeof(text),"%sdz:%f)",text,Node->dz);
}
return text;
}
double calc_angle_between_vectors_complex_rad(
const Vector_t* const v1,
const Vector_t* const v2) {
double arg_diff_rad = 0.0;
LOG_DEBUG(MATH,"V1:%s", VectorToStr(v1));
LOG_DEBUG(MATH,"V2:%s", VectorToStr(v2));
double complex X1= v1->dx - v1->dy * I;
double complex X2= v2->dx - v2->dy * I;
if(0.0<cabs(X1)) {
if(0.0<cabs(X2)) {
double x1_arg_rad = carg(X1);
double x2_arg_rad = carg(X2);
arg_diff_rad = x1_arg_rad-x2_arg_rad;
if (M_PI < arg_diff_rad) {
arg_diff_rad = arg_diff_rad-M_2_PI;
} else {
if(arg_diff_rad < -M_PI) {
arg_diff_rad =arg_diff_rad + M_2_PI;
}
}
}
}
LOG_DEBUG(MATH,"Theta:%f rad", arg_diff_rad);
return arg_diff_rad;
}
Отладка
Я написал консольное приложение для проверки функции вычисления угла между векторами. Как видно тесты проходят. Значит алгоритм работает.
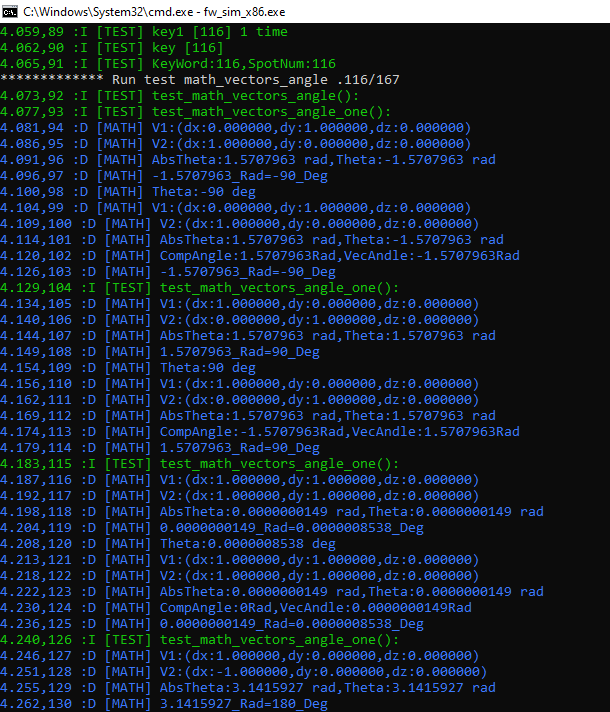
Вот еще несколько результатов вычислений.
Функция работает.
Достоинства
++Формализм, простота и понятность. Используются широко известные и общепризнанные математические методы линейной алгебры.
++Этот код можно использовать как эталон для тестирования более простых с вычислительной точки зрения алгоритмов вычисления углов между векторами.
Недостатки
--Данный способ вычисления угла между векторами весьма ёмкий с вычислительной точки зрения. Тут два корня, арккосинус, умножение и сложение.
Где обычно надо вычислять угол между векторами?
1--Везде, где есть нужда хоть чем-то поворачивать. Это PTZ камеры, астрономические телескопы, лазерные дальномеры расстояний до спутников GPS, тяжелые мельницы с приводом у лопастей, ветрогенераторы, турели, строительные краны, направленные антенны (ЯГИ, параболические, АФАРы), геодезические теодолиты, солнечные батареи. Там постоянно возникает задача определения угла между векторами и наведения опорно-поворотной платформы на какую-то цель.
2--В SDR обработке на стороне приёмника (как real-time так и в post-processing(е)) есть такая вещь как фазовый детектор. Фазовый детектор- это часть ФАПЧ цепей. Фазовый детектор с программной точки зрения - это как раз определитель угла между векторами, которые образованы двумя комплексными числами виде (I+jQ): фаза от LocalOscullator (LO) и фаза сигнала с делителя частоты на выходе.
3--Подразумеваю, что вычисление углов между векторами также нужно в разработке компьютерных игр.
Итоги
Удалось научиться вычислять угол между векторами. Алгоритм вычисления угла работает.
Как видите, чтобы определить угол между векторами надо знать тригонометрию, линейную алгебру, (скалярное произведение, векторное произведение) и вычислительные методы.
Было бы здорово если бы такая операция как найти угол между векторами была реализована на аппаратном уровне прямо среди набора поддерживаемых assembler команд.
Если вам известен более простой код для вычисления угла между векторами, то пишите в комментариях.
Словарь
Акроним |
Расшифровка |
PTZ |
Pan Tilt Zoom |
SDR |
Software-Defined Radio |
PLL |
Phase-locked loop |
CCW |
Counter Clock Wise |
CW |
Clock Wise |
ФАПЧ |
Фазовая автоподстройка частоты |
Ссылки
http://latex.codecogs.com/eqneditor/editor.php
https://rsdn.org/forum/alg/4415389.hot
Теория управления шаговым двигателем (или как вертеть PTZ камеру) https://habr.com/ru/articles/709500/
The Right Way to Calculate Stuff https://www.plunk.org/~hatch/rightway.html
Комментарии (102)

lorc
16.04.2024 21:57+8На разных микроконтроллерах, в Linux ядре, в User Spaсe и прочих программах.
Знаете что с вами сделают за попытку использовать floating point в ядре? Хинт: уж точно по головке не погладят.
Да и у многих МК нет аппаратной поддержки FP.

voldemar_d
16.04.2024 21:57+3Ну нет аппаратной поддержки - компилятор же позволяет создать код, который считает все эти функции. Вопрос лишь в скорости вычислений, но часто ли надо угол считать миллион раз в секунду? Да даже тысячу.

tminnigaliev
16.04.2024 21:57Можно через long long в fixed point всё посчитать, но придётся писать и библиотеку для триг.функций для такого самодельного фиксд пойнта.

voldemar_d
16.04.2024 21:57Когда я пишу для Arduino, в котором нет аппаратного floating point, на C++, компилятор всё сам сделает, зачем мне об этом задумываться?

Godless
16.04.2024 21:57+1Можно уйти в вычисления с фиксированной точкой.

voldemar_d
16.04.2024 21:57Можно, вопрос в целесообразности (в статье по ссылке есть еще раздел "минусы"). Зачем это делать? Один из случаев - когда за счет этого можно повысить быстродействие. Но всегда ли это критично?

Cubus
16.04.2024 21:57+1Задумываться не имеет смысла до тех пор, когда проект не перестанет влезать в RAM или ROM. Функции для работы с float, добавляемые компилятором, довольно большие.
Я на своей шкуре это испытал, пришлось переделывать на int проект - и он сразу влез :)
Надо сказать, для мелкой серии и штучных поделок можно просто купить МК с аппаратным float и не переживать, они нынче дешёвые.

strvv
16.04.2024 21:57+2более того можно использовать не радианы и градусы, а количество шагов двигателя. а в виду дискретности и конечности данного параметра можно подобрать целочисленные величины и даже множественные вычисления будут валидны.

voldemar_d
16.04.2024 21:57+4А почему, собственно, за такое не погладят по головке? Если это успешно решает поставленную задачу, скорости и точности хватает, то в чем проблема?
И что делать, если мне и вправду надо в коде МК синус вычислить?

Indemsys
16.04.2024 21:57+3В старых архитектурах процессоров в ядре OS не поддерживалось сохранение регистров сопроцесора. Либо это сохранение надо было задавать явно. Т.е. либо змедлялось переключение контекста и вся ось змедлялась, либо были сбои вычислений из-за применения сопроцесора floatpoint в ядре без корректного сохранения контекста. Сегодня архитектуры автоматически включают сохранение контекста сопроцессора для отдельных задач, да сопроцессоров стало больше, так что применять даже double в ядре - это нормально. Кому double медленно есть укороченый float, со скростью int. Кому нужен CORDIC, есть у STM микронтроллеры с сопроцессором CORDIC.

voldemar_d
16.04.2024 21:57+1либо были сбои вычислений из-за применения сопроцесора floatpoint
Такие сбои могли возникать при вычислении тригонометрических функций и квадратных корней?

Indemsys
16.04.2024 21:57+1Сбои возникают когда в ходе вычислений одна задача использующая сопроцессор вытесняет другую задачу тоже использующую сопроцессор. Сопроцесор, кстати, может использоваться даже при простом копировании памяти, где в помине нет floatpoint. Так делают супеоптимизирующие компиляторы. А все благодаря тому что ядра процессоров научились автоматически определять факт использования сопроцессора.
А скоро пойдут сопроцессоры для ИИ, и будет еще больше нюансов.
voldemar_d
16.04.2024 21:57+1Вы сейчас про какие конкретно процессоры и сопроцессоры пишете? Какие-то специфические или x86?

Indemsys
16.04.2024 21:57+2Я пишу про ARM 7...9, ARM Cortex M3..7..85. Т.е. те с которыми работает автор статьи.
Про x86 я ничего сказать не могу. Там даже система команд в последних процессорах не вся раскрыта. Так что мало кто квалифицировано может сказать про сопроцессоры x86.Простейшие Arduino не используют RTOS и сопроцессоров нет и там, конечно, проблемы с float point нет в принципе.

voldemar_d
16.04.2024 21:57+1В том коде, который автор привел в статье, какие реально могут быть проблемы при вычислениях с плавающей точкой? Теоретические, или Вы прямо сходу видите их?

Indemsys
16.04.2024 21:57+1В статье приведен лишь фрагмент кода. А какой код весь здесь и идет дискуссия.
Во-первых что там с RTOS, во-вторых что там с быстродействием (вдруг он в петле PID-а, а сам не детерминирован и тормозной), в-третьих что за архитектура чипа. И от этого всего зависит плох или хорош код.В целом если бы шла речь о ARM Cortex-M85 я бы такой код без сомнения применил бы. Никакие целочисленные оптимизации в случае M85 существенно код бы не ускорили.

Goron_Dekar
16.04.2024 21:57Проблема в том, что использование плавающей точки это чуть более легально, чем сырые указатели или адресная арефметика. Сама по себе технология плавающих точек исторически в компьютерах реализована из рук вон плохо ввиду дискретности самих вычислителей, и все хаки, которые позволяют с ней работать, требуют повышенного внимания, огромных затрат по вычислению и проверкам и постоянно приводят с неожиданным результатам. И ясно, что приёмы, обладающие такими недостатками, не приветствуются в коде ядра.
Если и вправду надо в коде МК вычислять синус, то гораздо краше было бы заранее задать точность и использовать "фиксированную точку" - целочисленную арифметику в долях. Это также часто приводит к странному, но всё-таки реже, чем FP.
Единственное место, где плавающая точка смотрится на месте - вывод. Например, графика и звук. Потому, что даже если возникнет какая-то погрешность, это не будет смертельно. Поэтому она и появилась в компьютерах примерно одновременно с графикой.

voldemar_d
16.04.2024 21:57+2использование плавающей точки это чуть более легально
Я довольно конкретно задал вопрос: а что, если использование чисел с плавающей точкой успешно решает поставленную задачу? Тогда в чём проблема?
Сама по себе технология плавающих точек исторически в компьютерах реализована из рук вон плохо ввиду дискретности самих вычислителей, и все хаки, которые позволяют с ней работать, требуют повышенного внимания, огромных затрат по вычислению и проверкам и постоянно приводят с неожиданным результатам.
Я в курсе, какие бывают проблемы при использовании чисел с плавающей точкой. Не уверен в том, что это прямо "постоянно приводит с неожиданным результатам" - может, у Вас просто задачи какие-то специфические?
Единственное место, где плавающая точка смотрится на месте - вывод. Например, графика и звук
А в каких задачах это не на месте? Мне правда интересно узнать, что это за задачи такие особенные. И чтобы это было актуально для программирования МК.

Goron_Dekar
16.04.2024 21:57+3Я довольно конкретно задал вопрос: а что, если использование чисел с плавающей точкой успешно решает поставленную задачу? Тогда в чём проблема?
Конкретный ответ: если ревьюверу кажется, что ваш код, решая поставленную задачу, усложняет поддержку проекта, он видит в этом проблему. Посмотрите на проблему с точки зрения лида, которому ваша фича менее важна, чем проект целиком, тогда и вы её увидите.
А в каких задачах это не на месте? Мне правда интересно узнать, что это
за задачи такие особенные. И чтобы это было актуально для
программирования МК.Это может быть не на месте когда вы пишите библиотеку, от которой требуется прогнозируемая производительность, но не гарантировано, что она будет использоваться в проектах только на МК с аппаратной поддержкой FP.

voldemar_d
16.04.2024 21:57если ревьюверу кажется, что ваш код, решая поставленную задачу, усложняет поддержку проекта, он видит в этом проблему
И что он предложит сделать? Перейти на целочисленную арифметику? Просто на всякий случай?
Это может быть не на месте
Я думал, что у Вас конкретный пример есть. Например, такой.
прогнозируемая производительность
Можно просто измерить производительность, вот она и станет прогнозируемой.

Indemsys
16.04.2024 21:57Я думал, что у Вас конкретный пример есть. Например, такой.
Забавно то что на протяжении всей статьи автор нигде не назвал тип сопроцессора и процессора. Как будьто программисты на PC работают на неких абстрактных, универсальных и одинаковых машинах.
Программист же микроконтроллеров знает мат. сопроцессор своего микроконтроллера как свои пять пальцев. Каждая операция с floatpoint проверяется на генерируемый ассемблерный код и использование регистров.
Если нужны тригонометрические функции, то преверяются все возможные варианты библиотечных функций на скорость и точность.

voldemar_d
16.04.2024 21:57+1ИМХО, всё зависит от решаемой задачи. Условно, если нужно несколько раз в секунду вычислять синус, и код в IDE пишется на C/C++, какая разница, во что он скомпилируется и какие регистры использует, если всё работает?
Я правда не пойму, каким кодом с вычислением тригонометрических функций можно что-то "сломать" в МК, потому и прошу какой-нибудь жизненный пример.

Indemsys
16.04.2024 21:57Видимо не имеете дело с RTOS, потому и не знаете. Тут просто надо глубже знать контекст.

voldemar_d
16.04.2024 21:57Конечно, не знаю. Потому и интересуюсь. Может, есть ссылка на что-то, где про это подробнее почитать можно?

Goron_Dekar
16.04.2024 21:57+1И что он предложит сделать?
Предложит не нарушать правила кодиинга, принятые в проекте. А вы бы на его месте что предложили?

voldemar_d
16.04.2024 21:57Так это зависит от того, есть ли такие правила, и от самого проекта. Если в проекте надо проводить вычисления, приведенные в статье, какие здесь могут быть подводные камни?

Goron_Dekar
16.04.2024 21:57+1Мы начали дискуссию не только со статьи, но и с замечания про то, что за попытки протащить в ядро (не очень понятно, какое, ну да ладно) кода с FP вас по головке не погладят. Я думаю, что это значит, что в разработке этого ядра FP либо в чёрном, либо в сером списке правил, даже если они не написаны. Согласны со мною?

strvv
16.04.2024 21:57немного ранее описал решение задачи - https://habr.com/ru/articles/807641/#comment_26739019
повторюсь, перефразируя:
Если можно использовать не радианы и градусы, а количество шагов двигателя, то в виду дискретности и конечности данного параметра (количества шагов на полный круг) можно подобрать целочисленные величины и даже множественные вычисления будут валидны.
Т.е. остаться в рамках дискретной математики, и т.к. как здесь обсуждалось, возможно, на кортексах - то long int спасёт отца российской демократии.

lorc
16.04.2024 21:57А почему, собственно, за такое не погладят по головке?
https://yarchive.net/comp/linux/kernel_fp.html
Если кратко - сохранять FP контекст при переключении в режим ядра - очень дорого. FP контекст переключается только когда переключаются поток в user land. Это происходит куда реже чем прыжки между user mode и kernel mode.

voldemar_d
16.04.2024 21:57+1Вы это в применении к МК пишете, или к x86?

lorc
16.04.2024 21:57Я это пише в применении к
в Linux ядре

voldemar_d
16.04.2024 21:57В письме пишется, если я правильно понял, про FP-сопроцессор в x86:
For a while now, x86-specific optimizations
В обсуждаемой статье речь про МК, и про ядро Linux ни слова. В чем связь?

lorc
16.04.2024 21:57+1В обсуждаемой статье речь про МК, и про ядро Linux ни слова. В чем связь?
Цитату про ядро я взял из статьи. Можете сами проверить.
В письме пишется, если я правильно понял, про FP-сопроцессор в x86:
Потому что Линус смотрит на вещи в основном с точки зрения x86. Но это относится и к другим архитектурам, например к ARM. FPU изредка используется для SIMD инструкций (например в коде raid6), но все такие места обложены
kernel_fpu_beginдля x86 илиkernel_neon_beginдля ARM.EDIT: В том коде, который может потенциально компилироваться под ARM нет вообще ни одной double или float переменной. Я вообще не уверен что порт ядра на ARM умеет работать с FP в ядерном контексте.

victor_1212
16.04.2024 21:57+2не совсем понимаю, чем для подобных приложений FP может быть полезен, дело в том что собственная механическая точность даже астрономической монтировки порядка единиц угловых минут, если в районе одной минуты, то уже вес механики хорошо за тонну будет, если в радианах это 4-5 значащих цифр, что должно быть достаточно, т.к. более точно определить угловые координаты в оптическом канале можно только относительным методом, например привязкой к звездному узору, причина таких ограничений проста - механика гнется, и подвержена вибрации

victor_1212
16.04.2024 21:57+3если интересно, попробуйте использовать ряд Тейлора, и сравнить результаты по точности и быстродействию, возможно удастся оптимизировать для конкретного применения


HEXFFFFFFFF
16.04.2024 21:57Ну задача очень узкая. Да и к программированию не имеет отношения. За 30 лет работы программистом с математикой сложнее арифметики 5й класс сталкивался буквально раза три. Хотя похожая задача была - для навигации, определить рассположен ли обьект на линии между двух точек, и если нет то на сколько гр. он должен повернуться что бы попасть обратно на линию. В общем математика не профильный предмет для программиста, все равно что пение для грузчика))))

Goron_Dekar
16.04.2024 21:57+2Даже не знаю, повезло вам, или нет. Когда занимался прямо вот разработкой плотно, из математики, такой, как фурье, линал или рпосто интегрирование со статистикой не вылезал вообще. Даже делали программу по модели из матлаба.
В обывательском кодинге, с которым имею дело сейчас, тоже присутствует много статистики, иногда линал. Хорошо, что задачи FTT на 8 битах и 4к флэша больше не стоят.

aabzel Автор
16.04.2024 21:57+3За 30 лет работы программистом с математикой сложнее арифметики 5й класс сталкивался буквально раза три.
Напрасно Вы так. @HEXFFFFFFFF
На самом деле в программировании микроконтроллеров целая куча всяческой математики, как школьной так и ВУЗ(овской).Вот подборка текстов в доказательство:
--Зачем Программисту Микроконтроллеров Диофантовы Уравнения
https://habr.com/ru/articles/803415/--Зачем Программисту Микроконтроллеров Численные Методы?
https://habr.com/ru/articles/700394/--Зачем Программисту Микроконтроллеров Математическая Статистика? (или так ли хороши UWB трансиверы?)
https://habr.com/ru/articles/712616/--Зачем программисту микроконтроллеров тригонометрия? (или Обзор Усилителя Звука из Apple AirTag)
https://habr.com/ru/articles/767386/
--Зачем программисту микроконтроллеров комплексные числа (или обзор MEMS микрофона MP23DB01HPTR)
https://habr.com/ru/articles/765896/--Комбинаторика нужна для модульных тестов
https://habr.com/ru/articles/762142/
https://habr.com/ru/articles/709374/--Грамматики Хомского нужны для CLI
https://habr.com/ru/articles/757122/--Математическая индукция
Сканирование шины RS485
https://habr.com/ru/articles/752292/--Спец разделы мат. анализа: Ряды
Ряд Фурье как Фильтр Нижних Частот
https://habr.com/ru/articles/748334/
https://habr.com/ru/articles/687640/--Бинарные деревья поиска
NVRAM Поверх off-chip SPI-NOR Flash
https://habr.com/ru/articles/732442/--Высший пилотаж алгебры
Вывод формулы для двустороннего определения дальности между UWB трансиверами
https://habr.com/ru/articles/723594/--Интегралы
Теория управления шаговым двигателем (или как вертеть PTZ камеру)
https://habr.com/ru/articles/709500/--Сферическая Геометрия Римана
https://habr.com/ru/articles/649163/
https://habr.com/ru/articles/648247/И это только то, с чем я лично сталкивался.
Может ещё что-то надо из математики.

tuxi
16.04.2024 21:57+8Если вычисления угла происходят много-много раз за единицу времени, то может быть каким-то образом использовать готовые таблицы для грубой оценки и потом применить более простые уточняющие вычисления? Сузить задачу с помощью таблиц до более простой.
Если же это требуется делать условно "1 раз в час" и есть гарантия (хотя о чем это я), что это не будет требоваться делать чаще, имеет ли практический смысл оптимизировать алгоритм?

aabzel Автор
16.04.2024 21:57В sdr обработке угол между векторами(комплексными числами) надо вычислять очень- очень часто.

diakin
16.04.2024 21:57+5Не очень понятно применение именно к задаче поворота антенны и пр.
У вас есть датчик текущего положения объектива. И есть желаемое направление положения объектива. Вам надо вычислить ошибку в градусах.
Если есть один угол и второй угол (как на картинке), то надо вычесть один из другого и все.

aabzel Автор
16.04.2024 21:57Если есть один угол и второй угол (как на картинке), то надо вычесть один из другого и все.
В условии задачи прописано, что надо чтобы результат выдавать чистый. То есть: -180....180 градусов.
Если просто наивно вычесть аргументы вот так:double calc_angle_between_vectors_naiv_rad( const Vector_t* const v1, const Vector_t* const v2) { double arg_diff_rad = 0.0; LOG_DEBUG(MATH,"V1:%s",VectorToStr(v1)); LOG_DEBUG(MATH,"V2:%s",VectorToStr(v2)); double complex X1=v1->dx - v1->dy * I; double complex X2=v2->dx - v2->dy * I; if(cabs(X1)){ if(cabs(X2)){ double x1_arg_rad = carg(X1); double x2_arg_rad = carg(X2); arg_diff_rad = x1_arg_rad-x2_arg_rad; } } LOG_DEBUG(MATH,"Theta:%f rad",arg_diff_rad); return arg_diff_rad; }вот что получится (см колонку angleNa). Колонка angleTr - это правильный результат.
+-----+------------+------------+--------+--------+------+-----+-----+ | No | A | B |angleTr |angleNa | diff | |A| | |B| | +-----+------------+------------+--------+--------+------+-----+-----+ | 0 | -1.0, -1.0 | -1.0, 0.0 | -45.0 | 315.0 | Diff | 1.4 | 1.0 | | 1 | -1.0, -1.0 | -1.0, 0.5 | -71.6 | 288.4 | Diff | 1.4 | 1.1 | | 2 | -1.0, -1.0 | -1.0, 1.0 | -90.0 | 270.0 | Diff | 1.4 | 1.4 | | 3 | -1.0, -1.0 | -0.5, 0.0 | -45.0 | 315.0 | Diff | 1.4 | 0.5 | | 4 | -1.0, -1.0 | -0.5, 0.5 | -90.0 | 270.0 | Diff | 1.4 | 0.7 | | 5 | -1.0, -1.0 | -0.5, 1.0 | -108.4 | 251.6 | Diff | 1.4 | 1.1 | | 6 | -1.0, -1.0 | 0.0, 0.5 | -135.0 | 225.0 | Diff | 1.4 | 0.5 | | 7 | -1.0, -1.0 | 0.0, 1.0 | -135.0 | 225.0 | Diff | 1.4 | 1.0 | | 8 | -1.0, -1.0 | 0.5, 1.0 | -161.6 | 198.4 | Diff | 1.4 | 1.1 | | 9 | -1.0, -0.5 | -1.0, 0.0 | -26.6 | 333.4 | Diff | 1.1 | 1.0 | | 10 | -1.0, -0.5 | -1.0, 0.5 | -53.1 | 306.9 | Diff | 1.1 | 1.1 | | 11 | -1.0, -0.5 | -1.0, 1.0 | -71.6 | 288.4 | Diff | 1.1 | 1.4 | | 12 | -1.0, -0.5 | -0.5, 0.0 | -26.6 | 333.4 | Diff | 1.1 | 0.5 | | 13 | -1.0, -0.5 | -0.5, 0.5 | -71.6 | 288.4 | Diff | 1.1 | 0.7 | | 14 | -1.0, -0.5 | -0.5, 1.0 | -90.0 | 270.0 | Diff | 1.1 | 1.1 | | 15 | -1.0, -0.5 | 0.0, 0.5 | -116.6 | 243.4 | Diff | 1.1 | 0.5 | | 16 | -1.0, -0.5 | 0.0, 1.0 | -116.6 | 243.4 | Diff | 1.1 | 1.0 | | 17 | -1.0, -0.5 | 0.5, 0.5 | -161.6 | 198.4 | Diff | 1.1 | 0.7 | | 18 | -1.0, -0.5 | 0.5, 1.0 | -143.1 | 216.9 | Diff | 1.1 | 1.1 | | 19 | -1.0, -0.5 | 1.0, 1.0 | -161.6 | 198.4 | Diff | 1.1 | 1.4 | | 20 | -1.0, 0.0 | -1.0, -1.0 | 45.0 | -315.0 | Diff | 1.0 | 1.4 | | 21 | -1.0, 0.0 | -1.0, -0.5 | 26.6 | -333.4 | Diff | 1.0 | 1.1 | | 22 | -1.0, 0.0 | -0.5, -1.0 | 63.4 | -296.6 | Diff | 1.0 | 1.1 | | 23 | -1.0, 0.0 | -0.5, -0.5 | 45.0 | -315.0 | Diff | 1.0 | 0.7 | | 24 | -1.0, 0.0 | 0.0, -1.0 | 90.0 | -270.0 | Diff | 1.0 | 1.0 | | 25 | -1.0, 0.0 | 0.0, -0.5 | 90.0 | -270.0 | Diff | 1.0 | 0.5 | | 26 | -1.0, 0.0 | 0.5, -1.0 | 116.6 | -243.4 | Diff | 1.0 | 1.1 | | 27 | -1.0, 0.0 | 0.5, -0.5 | 135.0 | -225.0 | Diff | 1.0 | 0.7 | | 29 | -1.0, 0.0 | 1.0, -1.0 | 135.0 | -225.0 | Diff | 1.0 | 1.4 | | 30 | -1.0, 0.0 | 1.0, -0.5 | 153.4 | -206.6 | Diff | 1.0 | 1.1 | | 32 | -1.0, 0.5 | -1.0, -1.0 | 71.6 | -288.4 | Diff | 1.1 | 1.4 | | 33 | -1.0, 0.5 | -1.0, -0.5 | 53.1 | -306.9 | Diff | 1.1 | 1.1 | | 34 | -1.0, 0.5 | -0.5, -1.0 | 90.0 | -270.0 | Diff | 1.1 | 1.1 | | 35 | -1.0, 0.5 | -0.5, -0.5 | 71.6 | -288.4 | Diff | 1.1 | 0.7 | | 36 | -1.0, 0.5 | 0.0, -1.0 | 116.6 | -243.4 | Diff | 1.1 | 1.0 | | 37 | -1.0, 0.5 | 0.0, -0.5 | 116.6 | -243.4 | Diff | 1.1 | 0.5 | | 38 | -1.0, 0.5 | 0.5, -1.0 | 143.1 | -216.9 | Diff | 1.1 | 1.1 | | 39 | -1.0, 0.5 | 0.5, -0.5 | 161.6 | -198.4 | Diff | 1.1 | 0.7 | | 40 | -1.0, 0.5 | 1.0, -1.0 | 161.6 | -198.4 | Diff | 1.1 | 1.4 | | 42 | -1.0, 1.0 | -1.0, -1.0 | 90.0 | -270.0 | Diff | 1.4 | 1.4 | | 43 | -1.0, 1.0 | -1.0, -0.5 | 71.6 | -288.4 | Diff | 1.4 | 1.1 | | 44 | -1.0, 1.0 | -0.5, -1.0 | 108.4 | -251.6 | Diff | 1.4 | 1.1 | | 45 | -1.0, 1.0 | -0.5, -0.5 | 90.0 | -270.0 | Diff | 1.4 | 0.7 | | 46 | -1.0, 1.0 | 0.0, -1.0 | 135.0 | -225.0 | Diff | 1.4 | 1.0 | | 47 | -1.0, 1.0 | 0.0, -0.5 | 135.0 | -225.0 | Diff | 1.4 | 0.5 | | 48 | -1.0, 1.0 | 0.5, -1.0 | 161.6 | -198.4 | Diff | 1.4 | 1.1 | | 51 | -0.5, -1.0 | -1.0, 0.0 | -63.4 | 296.6 | Diff | 1.1 | 1.0 | | 52 | -0.5, -1.0 | -1.0, 0.5 | -90.0 | 270.0 | Diff | 1.1 | 1.1 | | 53 | -0.5, -1.0 | -1.0, 1.0 | -108.4 | 251.6 | Diff | 1.1 | 1.4 | | 54 | -0.5, -1.0 | -0.5, 0.0 | -63.4 | 296.6 | Diff | 1.1 | 0.5 | | 55 | -0.5, -1.0 | -0.5, 0.5 | -108.4 | 251.6 | Diff | 1.1 | 0.7 | | 56 | -0.5, -1.0 | -0.5, 1.0 | -126.9 | 233.1 | Diff | 1.1 | 1.1 | | 57 | -0.5, -1.0 | 0.0, 0.5 | -153.4 | 206.6 | Diff | 1.1 | 0.5 | | 58 | -0.5, -1.0 | 0.0, 1.0 | -153.4 | 206.6 | Diff | 1.1 | 1.0 | | 59 | -0.5, -0.5 | -1.0, 0.0 | -45.0 | 315.0 | Diff | 0.7 | 1.0 | | 60 | -0.5, -0.5 | -1.0, 0.5 | -71.6 | 288.4 | Diff | 0.7 | 1.1 | | 61 | -0.5, -0.5 | -1.0, 1.0 | -90.0 | 270.0 | Diff | 0.7 | 1.4 | | 62 | -0.5, -0.5 | -0.5, 0.0 | -45.0 | 315.0 | Diff | 0.7 | 0.5 | | 63 | -0.5, -0.5 | -0.5, 0.5 | -90.0 | 270.0 | Diff | 0.7 | 0.7 | | 64 | -0.5, -0.5 | -0.5, 1.0 | -108.4 | 251.6 | Diff | 0.7 | 1.1 | | 65 | -0.5, -0.5 | 0.0, 0.5 | -135.0 | 225.0 | Diff | 0.7 | 0.5 | | 66 | -0.5, -0.5 | 0.0, 1.0 | -135.0 | 225.0 | Diff | 0.7 | 1.0 | | 67 | -0.5, -0.5 | 0.5, 1.0 | -161.6 | 198.4 | Diff | 0.7 | 1.1 | | 68 | -0.5, 0.0 | -1.0, -1.0 | 45.0 | -315.0 | Diff | 0.5 | 1.4 | | 69 | -0.5, 0.0 | -1.0, -0.5 | 26.6 | -333.4 | Diff | 0.5 | 1.1 | | 70 | -0.5, 0.0 | -0.5, -1.0 | 63.4 | -296.6 | Diff | 0.5 | 1.1 | | 71 | -0.5, 0.0 | -0.5, -0.5 | 45.0 | -315.0 | Diff | 0.5 | 0.7 | | 72 | -0.5, 0.0 | 0.0, -1.0 | 90.0 | -270.0 | Diff | 0.5 | 1.0 | | 73 | -0.5, 0.0 | 0.0, -0.5 | 90.0 | -270.0 | Diff | 0.5 | 0.5 | | 74 | -0.5, 0.0 | 0.5, -1.0 | 116.6 | -243.4 | Diff | 0.5 | 1.1 | | 75 | -0.5, 0.0 | 0.5, -0.5 | 135.0 | -225.0 | Diff | 0.5 | 0.7 | | 77 | -0.5, 0.0 | 1.0, -1.0 | 135.0 | -225.0 | Diff | 0.5 | 1.4 | | 78 | -0.5, 0.0 | 1.0, -0.5 | 153.4 | -206.6 | Diff | 0.5 | 1.1 | | 80 | -0.5, 0.5 | -1.0, -1.0 | 90.0 | -270.0 | Diff | 0.7 | 1.4 | | 81 | -0.5, 0.5 | -1.0, -0.5 | 71.6 | -288.4 | Diff | 0.7 | 1.1 | | 82 | -0.5, 0.5 | -0.5, -1.0 | 108.4 | -251.6 | Diff | 0.7 | 1.1 | | 83 | -0.5, 0.5 | -0.5, -0.5 | 90.0 | -270.0 | Diff | 0.7 | 0.7 | | 84 | -0.5, 0.5 | 0.0, -1.0 | 135.0 | -225.0 | Diff | 0.7 | 1.0 | | 85 | -0.5, 0.5 | 0.0, -0.5 | 135.0 | -225.0 | Diff | 0.7 | 0.5 | | 86 | -0.5, 0.5 | 0.5, -1.0 | 161.6 | -198.4 | Diff | 0.7 | 1.1 | | 89 | -0.5, 1.0 | -1.0, -1.0 | 108.4 | -251.6 | Diff | 1.1 | 1.4 | | 90 | -0.5, 1.0 | -1.0, -0.5 | 90.0 | -270.0 | Diff | 1.1 | 1.1 | | 91 | -0.5, 1.0 | -0.5, -1.0 | 126.9 | -233.1 | Diff | 1.1 | 1.1 | | 92 | -0.5, 1.0 | -0.5, -0.5 | 108.4 | -251.6 | Diff | 1.1 | 0.7 | | 93 | -0.5, 1.0 | 0.0, -1.0 | 153.4 | -206.6 | Diff | 1.1 | 1.0 | | 94 | -0.5, 1.0 | 0.0, -0.5 | 153.4 | -206.6 | Diff | 1.1 | 0.5 | | 96 | 0.0, -1.0 | -1.0, 0.0 | -90.0 | 270.0 | Diff | 1.0 | 1.0 | | 97 | 0.0, -1.0 | -1.0, 0.5 | -116.6 | 243.4 | Diff | 1.0 | 1.1 | | 98 | 0.0, -1.0 | -1.0, 1.0 | -135.0 | 225.0 | Diff | 1.0 | 1.4 | | 99 | 0.0, -1.0 | -0.5, 0.0 | -90.0 | 270.0 | Diff | 1.0 | 0.5 | | 100 | 0.0, -1.0 | -0.5, 0.5 | -135.0 | 225.0 | Diff | 1.0 | 0.7 | | 101 | 0.0, -1.0 | -0.5, 1.0 | -153.4 | 206.6 | Diff | 1.0 | 1.1 | | 102 | 0.0, -0.5 | -1.0, 0.0 | -90.0 | 270.0 | Diff | 0.5 | 1.0 | | 103 | 0.0, -0.5 | -1.0, 0.5 | -116.6 | 243.4 | Diff | 0.5 | 1.1 | | 104 | 0.0, -0.5 | -1.0, 1.0 | -135.0 | 225.0 | Diff | 0.5 | 1.4 | | 105 | 0.0, -0.5 | -0.5, 0.0 | -90.0 | 270.0 | Diff | 0.5 | 0.5 | | 106 | 0.0, -0.5 | -0.5, 0.5 | -135.0 | 225.0 | Diff | 0.5 | 0.7 | | 107 | 0.0, -0.5 | -0.5, 1.0 | -153.4 | 206.6 | Diff | 0.5 | 1.1 | | 108 | 0.0, 0.5 | -1.0, -1.0 | 135.0 | -225.0 | Diff | 0.5 | 1.4 | | 109 | 0.0, 0.5 | -1.0, -0.5 | 116.6 | -243.4 | Diff | 0.5 | 1.1 | | 110 | 0.0, 0.5 | -0.5, -1.0 | 153.4 | -206.6 | Diff | 0.5 | 1.1 | | 111 | 0.0, 0.5 | -0.5, -0.5 | 135.0 | -225.0 | Diff | 0.5 | 0.7 | | 114 | 0.0, 1.0 | -1.0, -1.0 | 135.0 | -225.0 | Diff | 1.0 | 1.4 | | 115 | 0.0, 1.0 | -1.0, -0.5 | 116.6 | -243.4 | Diff | 1.0 | 1.1 | | 116 | 0.0, 1.0 | -0.5, -1.0 | 153.4 | -206.6 | Diff | 1.0 | 1.1 | | 117 | 0.0, 1.0 | -0.5, -0.5 | 135.0 | -225.0 | Diff | 1.0 | 0.7 | | 120 | 0.5, -1.0 | -1.0, 0.0 | -116.6 | 243.4 | Diff | 1.1 | 1.0 | | 121 | 0.5, -1.0 | -1.0, 0.5 | -143.1 | 216.9 | Diff | 1.1 | 1.1 | | 122 | 0.5, -1.0 | -1.0, 1.0 | -161.6 | 198.4 | Diff | 1.1 | 1.4 | | 123 | 0.5, -1.0 | -0.5, 0.0 | -116.6 | 243.4 | Diff | 1.1 | 0.5 | | 124 | 0.5, -1.0 | -0.5, 0.5 | -161.6 | 198.4 | Diff | 1.1 | 0.7 | | 125 | 0.5, -0.5 | -1.0, 0.0 | -135.0 | 225.0 | Diff | 0.7 | 1.0 | | 126 | 0.5, -0.5 | -1.0, 0.5 | -161.6 | 198.4 | Diff | 0.7 | 1.1 | | 127 | 0.5, -0.5 | -0.5, 0.0 | -135.0 | 225.0 | Diff | 0.7 | 0.5 | | 129 | 0.5, 0.5 | -1.0, -0.5 | 161.6 | -198.4 | Diff | 0.7 | 1.1 | | 131 | 0.5, 1.0 | -1.0, -1.0 | 161.6 | -198.4 | Diff | 1.1 | 1.4 | | 132 | 0.5, 1.0 | -1.0, -0.5 | 143.1 | -216.9 | Diff | 1.1 | 1.1 | | 134 | 0.5, 1.0 | -0.5, -0.5 | 161.6 | -198.4 | Diff | 1.1 | 0.7 | | 135 | 1.0, -1.0 | -1.0, 0.0 | -135.0 | 225.0 | Diff | 1.4 | 1.0 | | 136 | 1.0, -1.0 | -1.0, 0.5 | -161.6 | 198.4 | Diff | 1.4 | 1.1 | | 137 | 1.0, -1.0 | -0.5, 0.0 | -135.0 | 225.0 | Diff | 1.4 | 0.5 | | 138 | 1.0, -0.5 | -1.0, 0.0 | -153.4 | 206.6 | Diff | 1.1 | 1.0 | | 139 | 1.0, -0.5 | -0.5, 0.0 | -153.4 | 206.6 | Diff | 1.1 | 0.5 | | 142 | 1.0, 1.0 | -1.0, -0.5 | 161.6 | -198.4 | Diff | 1.4 | 1.1 | +-----+------------+------------+--------+--------+------+-----+-----+В общем, просто вычитанием комплексных аргументов неправильный результат получается.
Если angleNa подать на вход системы управления для PTZ камеры, то она будет танцевать голубиным танцем.
diakin
16.04.2024 21:57+3if angle > 180 then angle= angle-360 if angle < -180 then angle= angle+360просто еще добавить проверку

aabzel Автор
16.04.2024 21:57Да, Вы @diakin правы.
Эта функция дает тот же результат что и calc_angle_between_vectors_raddouble calc_angle_between_vectors_naiv_rad( const Vector_t* const v1, const Vector_t* const v2) { double arg_diff_rad = 0.0; LOG_DEBUG(MATH,"V1:%s",VectorToStr(v1)); LOG_DEBUG(MATH,"V2:%s",VectorToStr(v2)); double complex X1=v1->dx - v1->dy * I; double complex X2=v2->dx - v2->dy * I; if(cabs(X1)){ if(cabs(X2)){ double x1_arg_rad = carg(X1); double x2_arg_rad = carg(X2); arg_diff_rad = x1_arg_rad-x2_arg_rad; if(M_PI < arg_diff_rad){ arg_diff_rad = arg_diff_rad-M_2_PI; }else { if(arg_diff_rad < -M_PI) { arg_diff_rad =arg_diff_rad + M_2_PI; } } } } LOG_DEBUG(MATH,"Theta:%f rad",arg_diff_rad); return arg_diff_rad; }

diakin
16.04.2024 21:57Но я больше к тому, откуда вообще берутся исходные данные в виде координат векторов x1, x2? Я бы понял, если бы это были угол и длина, а не координаты. Но что в данном случае будет длиной вектора? Расстояние до объекта? А зачем оно для поворота камеры?

aabzel Автор
16.04.2024 21:57+1Но я больше к тому, откуда вообще берутся исходные данные в виде координат векторов x1, x2?
Если говорить про SDR обработку, то это ADC семплы вида (I+j*Q) от цифрового смесителя.
Если говорить про уличную PTZ камеру, то в качестве цели могут просто прислать широту и долготу на которую надо навести объектив.

voldemar_d
16.04.2024 21:57+3Сравнение чисел с плавающей точкой правильнее делать, приводя к целому числу с умножением, например, на 1000 (зависит от нужной точности).
Fedorkov
16.04.2024 21:57+2Почему именно так?
Во всяком случае, от погрешности вычислений это не спасает (точнее, спасает с вероятностью < 1). Для этого нужно сравнивать через эпсилон.

voldemar_d
16.04.2024 21:57Сравнение чисел с плавающей точкой "в лоб" - источник разных сюрпризов из-за особенностей компилятора, платформы и т.д. Когда число приведено к целому, с ним сюрпризов, скажем так, гораздо меньше.
Fedorkov
16.04.2024 21:57А можно пример таких компиляторов и платформ?
Если не рассматривать NaN-ы и погрешности вычислений, некорректное сравнение двух чисел мне кажется слишком очевидным багом в платформе, чтобы программисту беспокоиться об этом.

voldemar_d
16.04.2024 21:57Оно не то что некорректное. Бывают разные сюрпризы. И их нужно иметь ввиду.
Fedorkov
16.04.2024 21:57+1Забавно, я тоже лет 10 назад обнаружил, что .NET в 32 битах использует 80-битный сопроцессор, а в 64 битах — 64-битный SSE2 (наверное, потому что x64 появился после SSE2, и все существующие процессоры на этой архитектуре поддерживают SSE2), и что это даёт разные результаты вычислений. Но у меня это был не баг, я просто из любопытства читал сгенерированные инструкции.
Но всё равно суммарное время, которое все пострадавшие потратили на исправление этого бага сильно меньше суммарного времени, которое миллионы программистов потратили бы на использование вашего способа везде, где только можно.

voldemar_d
16.04.2024 21:57Всегда нужно брать в расчёт целесообразность использования каждого из методов. И у целочисленной арифметики тоже есть свои сюрпризы.
потому что x64 появился после SSE2, и все существующие процессоры на этой архитектуре поддерживают SSE2
Так и есть.
Но у меня это был не баг
Задача в том и состоит, чтобы написанный код независимо от архитектуры выдавал одинаковый результат. Либо, даже если результат разный, это не должно приводить к непредсказуемым и/или фатальным последствиям.
которое миллионы программистов потратили бы на использование вашего способа везде, где только можно
Я не знаю про миллионы других программистов. При написании любого кода, даже не использующего арифметику с плавающей точкой, существуют наборы рекомендаций по поводу того, как лучше писать код. Следовать им или нет - выбор каждого.
Fedorkov
16.04.2024 21:57Рекомендации должны приносить больше пользы, чем вреда. Если вы при разработке обычной игры решите строго следовать всем рекомендациям какой-нибудь MISRA C, это практически гарантированно даст больше вреда за счёт возросших трудозатрат.
И кстати, ваш вариант всё равно не поможет, если в результате 64-битного вычисления получится 0.999...999, а в результате 80-битного — 1.000...001.

voldemar_d
16.04.2024 21:57Кто-то же три плюса моей рекомендации поставил. И я её тоже не сам придумал. Я не отрицаю, что бывают ситуации, когда так делать не стоит.
ваш вариант всё равно не поможет, если в результате 64-битного вычисления получится 0.999...999, а в результате 80-битного — 1.000...001
Почему не сработает? Хотите сказать, вот тут в res может получиться false?
double a = 0.9999999, b = 1.0000001; uint64_t ia = uint64_t(a * 1000.0 + 0.5), ib = uint64_t(b * 1000.0 + 0.5); bool res = (ia == ib);Да, правильнее было написать "округлить", конечно.

ejka
16.04.2024 21:57Теперь сравните c и d порядка 10^100

voldemar_d
16.04.2024 21:57Само собой, прежде чем решать любую проблему, надо выбирать соответствующий инструмент, который сможет её решить. У каждого инструмента есть свои ограничения.
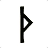
Fedorkov
16.04.2024 21:57Вы просто сместили критическую точку на 0.5.
Ваш код сломается на 0.0004999...999 == 0.0005000...001.
Кто-то же три плюса моей рекомендации поставил.
Меня плюсуют и за гораздо большие глупости. :))

voldemar_d
16.04.2024 21:57А кто сказал, что эти два числа нужно считать равными? И в какой именно задаче?
Например, мой способ подойдёт для сравнения частоты кадров в видеофайлах.
Fedorkov
16.04.2024 21:57В любой задаче, в которой x87 и SSE2 могут дать результат чуть больше и чуть меньше 0.0005, и где эти результаты нужно сравнивать.

voldemar_d
16.04.2024 21:57Я не спорю, что можно без проблем придумать ситуацию, в которой такое сравнение не сработает. Я привел задачу, взятую из реальной многолетней практики.

premierhr
16.04.2024 21:57+3два деления на корень можно заменить на умножение обратного корня. Была статья на Хабре про интересный алгоритм обратного корня тут: https://habr.com/ru/articles/730872/ Учитывая озвученную специфику применения для МК не сильно обремененного специальными инструкциями вполне можно попробовать.

lamerok
16.04.2024 21:57+1написал консольное приложение для проверки функции вычисления угла между векторами.
Для этого специально есть такое понятие как юнит тест, запускаете вместе с компиляцей, если прошли, то и сборка создалась, нет, ищете ошибку.
CppUTest можете использовать, подходит ко всем контроллерам.
Ещё и покрытие можете отслеживать, чтобы убедиться, что все ветки проверены.

klimkinMD
16.04.2024 21:57+2Для определения знака, поверните систему координат (простое линейное преобразование, без косинусов!) так, чтобы направление на цель совпадало с осью x (штрих) и по знаку ординаты нового вектора направления камеры определите, куда вращать. (т. е. нужно, просто, вычислить знак новой ординаты вектора направления на камеру)

bigcrush
16.04.2024 21:57+3Так в статье это делается с помощью векторного произведения, также никаких косинусов.

wataru
16.04.2024 21:57+7Если вам только понять, в какую сторону вращать, то вам достаточно знака угла. И тут даже тригонометрических функций не надо - просто смотрите на знак векторного произведения на плоскости (забейте на нулевые x компоненты векторов). Ведь на плоскости векторное произведение будет равно синусу угла, помноженному на длины векторов.

alekseykostromin
16.04.2024 21:57Обратный квадратный корень из квейка, если допустима погрешность https://ru.m.wikipedia.org/wiki/Быстрый_обратный_квадратный_корень

malishich
16.04.2024 21:57Написаная вами функция (7) в вычислительном плане очень плохо ведёт себя в районе -1 и +1, сам сталкивался с эффектом накопления ошибки. Почитайте http://www.plunk.org/~hatch/rightway.html (раздел "angle between unit vectors").

idimus
16.04.2024 21:57+3Окей. Я игровой программист, и вычислять углы между векторами, это мое повседневное.
Если бы мне нужно было бы составить эталонную функцию, я бы взял, кусочек математики из какого нить опенсорсного игрового движка (например мне проще всего взять математику из AzCore от Amazon Lumberyard только эту часть https://github.com/aws/lumberyard/tree/master/dev/Code/Framework/AzCore) и работать с этим.
Но с этой частью вы уже справились)))
Что бы я сделал с формулой для микрокорнтроллеров?:
- взял бы дешевый арккосинус https://stackoverflow.com/questions/3380628/fast-arc-cos-algorithm
- взял бы дешевый обратный корень отсюда (как таковой в функции корень квадратный не нужен ведь?) https://habr.com/ru/companies/infopulse/articles/336110/
Либо: зафигачил бы таблицу поиска для этих значений, с заданной точностью: то есть это просто захардкоженный массив данных (а-ля таблица брадиса), для разных значений углов. Памяти оно конечно немного отожрёт, но будет работать быстро с заданной точностью.
victor_1212
16.04.2024 21:57подход понятный например для игр, для более серьезных дел требуется проверка и анализ какие именно ошибки получаются, если использовать таблицы, также интерполяция может быть полезной (не обязательно линейная), просто таблицы меньше могут быть

idimus
16.04.2024 21:57Для более серьезных дел: таблички с заданной погрешностью и интерполяция; либо не срезать углы и делать честные вычисления, без аппроксимаций. Но послежний вопрос был, про то, кск снизить вычислительную сложность на контроллере...

victor_1212
16.04.2024 21:57верно, с небольшим дополнением - "честные вычисления, без аппроксимаций" это скорее абстракция, тем более на контроллере, как стандартные функции реализованы сам по себе серьезный вопрос, всегда нужен грамотный компромисс, также, как уже написал, не совсем понимаю зачем вообще FP надо для описанных приложений, типа нет там потребностей в такой точности, но автору виднее, конечно знаю когда и FP может не хватать, хотя к данной теме не относится

Indemsys
16.04.2024 21:57А embededder бы не стал тратить время медленные софтварные решения, а взял бы готовый ARM с DSP сопроцессором типа такого. И имел бы не только вычисления тригонометрии за десяток тактов, но и фильтры и матрици и все отстальное


idimus
16.04.2024 21:57До момента, у нас на складе 2000 тыщ таких то железок, и это будет основой для нашей аппаратной платформы... А так то да, мощные решения, в компактном корпусе и за дешево, в наше время на рынке присутствуют, и разнице в цене, иногда может оказаться минимальной. Но может автор, просто хочет пофлексить, на том железе что есть, потому что!

aabzel Автор
16.04.2024 21:57+1Я игровой программист, и вычислять углы между векторами, это мое повседневное.
Вспоминаю как я впервые делал вычисление угла между векторами для моделирования автоматического беспилотного управления гусеничными шасси для БМП-3 в своем магистерском исследовании.
Тоже своего рода GameDev только в стенах военного НИИ с тремя КПП и колючей проволокой на заборе.

idimus
16.04.2024 21:57+1Нуу, gamedev, это вам не рокет сайнс. Рокет санс, по прощу будет: детерминированное железо, более детерминированные условия и спецификации. Но да, симуляция реального мира, во время близкое к риал тайму, еще и с синхронизацией по сети, задачка мягко говоря, нетривиальная.
В то же время, рокет сайнс, ближе к тому, как сделать квадрокоптер, просто систем больше, и они сложнее. Так что если вы повернули БМП. то и квадрик можно пилить уверенно...

MrLantasire
16.04.2024 21:57Есть вариант решения задачи на плоскости через комплексные числа. Угол, с учётом знака, между комплексными числами a и b будет являться аргумент комплексного числа c, где c = a/b.
Другими словами fi = Arg(a/b).

wataru
16.04.2024 21:57+1И как же этот аргумент, собственно, вычислить?

MrLantasire
16.04.2024 21:57z = x + y*i
arg(z) вычисляется следующими способами:
arg(z) = arccos(x / |z|)
arg(z) = arcsin(y / |z|)
arg(z) = arctg(y / x)
Опуская вывод после fi = Arg(a/b) можно получить следующее:
fi = arctg( (xb * ya - xa * yb) / (xa*xb + ya*yb) )

wataru
16.04.2024 21:57Ну вот вы и пришли почти к тому же, что и в статье. Автор остановился на arccos, но в комментах выше уже несколько раз предлагали использовать арктангенс, векторное и скалярные произведения - последнюю формулу.

zar_10
16.04.2024 21:57«Зачем программисту микроконтроллеров линейная алгебра» или «как решать задачу способом, для неё не предназначенным» (в данном случае).
Угол между двумя векторами ищется через пару atan2 и одно ветвление. И то, atan2 только в случае, если мы не знаем ориентацию вектора (то есть, если камера смотрела в «ноль» и повернулась на 90°, то нам не нужно выяснять её ориентацию).
Итак. Используется определение полнокругового пеленга — любой угол поворота вектора отсчитывается от «северного» направления по часовой стрелке и имеет значение от 0° до 360°. Пусть мы знаем два угла пеленга векторов А и Б: А = 80°; Б = 280°. Задача: повернуть А к Б:
шаг 1: находим больший угол (это, очевидно, Б);
шаг 2: из большего угла вычитаем меньший — delta = 200°;
шаг 3: если delta <= 180°, значит должен произойти поворот по часовой стрелке на величину «Б-А»; иначе — против часовой стрелки на величину «360° - Б + А».
шаг 4: совершить поворот.
Если же известны только векторы, то с помощью atan2 (со всеми вытекающими в виде прописанных в любых спецификациях ограничений и исключений для этой функции, которые автор решил бахнуть вручную), мы выясняем углы векторов, отсчитываемые от «восточного» направления и прибавляем к по 90°, чтобы привести их к углам пеленга (но это, очевидно, никак не повлияет на результат — просто приведение к радарной терминологии).
Сколько линейной алгебры я использовал? По большому счёту, я, как программист, даже не должен знать как atan2 работает — возвращает полнокруговой угол и спасибо. Какое скалярное произведение — Бог с Вами (расчётов даже больше).
victor_1212
16.04.2024 21:57По большому счёту, я, как программист, даже не должен знать как atan2 работает
не для всех архитектур так просто, atan2 может быть реализован разными методами, с разными затратами, или не реализован, обсуждение можно найти на stackoverflow, если интересно посмотрите сравнение методов:
"Fast computation of arctangent functions for embedded applications ..." -





Uranix
Кажется это проще
aabzel Автор
Это система уравнений.
А чтобы это в код прописать надо преобразовать к виду
одной формулы
theta = fun(ax,ay,bx,by).
FGV
teta=atan2(ax*bx+ay*by,ax*by-ay*bx)
так покатит? (знаки не учел, лень думать)
Uranix
именно, только порядок аргументов поменять (векторное произведение ~ синус угла, скалярное ~ косинус)
FGV
угу. вечно забываю что в си у атан2 у первым идет :(
Fedorkov
Не только в Си, во всех языках.
FGV
ну вот это видимо не язык: https://learn.microsoft.com/ru-ru/office/vba/api/excel.worksheetfunction.atan2
Fedorkov
Ого, в Википедии этому даже часть статьи посвятили.
aabzel Автор
Покатит/ не покатит - покажут только модульные тесты.
ejka
theta=atan2(ax*by-ay*bx, ax*bx+ay*by)