В статье завершим цикл материалов по преобразованию MIDI-времени в другие форматы. Попутно столкнёмся с неожиданным приступом оверинжиниринга, напишем микроскопическое количество кода и откроем для себя неправильную музыку.

Как в современном мире устроен процесс создания музыки? Забыв про любителей исключительно тёплых аналоговых методов, выглядит алгоритм в общих чертах так: открыть на компьютере DAW, записать инструменты, сделать программные подложки синтезаторов, сэмплеров и т.п., повесить нужные обработки, свести, отмастерить.

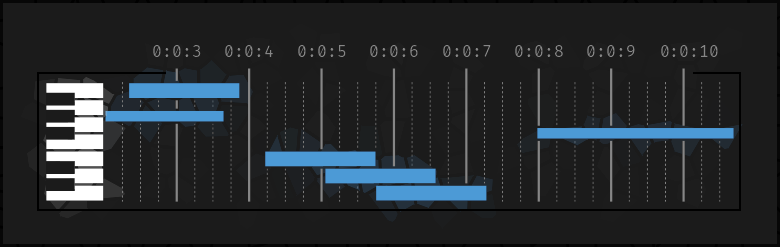
Касательно дорожек с виртуально созданными нотами, вы не сможете пройти мимо чуда человеческой мысли — piano roll:

Да, ссылка на описание ленты для механического пианино, причём тут компьютеры? Просто немного интересных фактов: используемый с 1980-х в программных музыкальных комбайнах piano roll уходит корнями к физическим машинам. К слову, ленты для них производятся до сих пор. Например, QRS Music Technology предлагает таковые на рождественскую тематику. Рождество, камин, механическое пианино…

Если же вы сядете за фортепиано обыкновенное, с клавишами и струнами, то музыкальное произведение предстанет перед вами на нотном стане, где различные геометрические фигуры дадут информацию по длительностям. Причём длительности эти являются по сути математическими дробями. Четвертная это 1/4, половинная — 1/2, половинная с точкой — 3/4, и т.п.

В MIDI, как мы уже знаем, время представляется числами, напрямую не привязанными к форматам, понятным homo sapiens. И хотя мы уже научились превращать такие числа в такты и доли, а также в секунды, минуты и иже с ними, нам осталось рассмотреть дроби, дабы закрыть тему с преобразованием времени из MIDI в различные представления. Чем мы и займёмся далее.

Время в виде математической дроби будем называть музыкальным (musical), дабы как-то его отличать от изученных нами ранее форматов.

Оглавление

• MIDI в музыкальное время

  • Когда просто — не вариант

  • Ничего сложного

• Музыкальное время в MIDI

• Заключение

MIDI в музыкальное время

Сразу к делу. У нас есть время в тиках T. Мы хотим понять, какой музыкальной длительности (дроби x/y) оно соответствует. Зная длительность четвертной ноты в тиках (ticks per quarter note, TPQN, см. Время в MIDI), составляем простейшую пропорцию:

x/y = T
1/4 = TPQN

или

x/y = T/(4⋅TPQN)

Когда просто — не вариант

В 2017-м году на этом месте электрика моего мозга дала сбой. Зачем-то я подумал: “А почему бы не избавиться от дробей и посмотреть, что получится?”. Умножив обе части равенства на 4⋅TPQN⋅y, получим

4⋅TPQN⋅x = T⋅y

или

4⋅TPQN⋅x - T⋅y = 0

“Такое решать я не умею” — пронеслась в голове мысль. — “Но, кажется, что-то такое мы проходили в университете”. Погуляв немного по просторам сети, я понял, что такие вещи мы действительно изучали, и называются они диофантовыми уравнениями. Если точнее, перед нами однородное диофантово уравнение.

Уже лучше, мы знаем, с чем имеем дело. Но учёба в университете закончилась 3 года назад, математика не была любимым предметом, а потому ищем дальше.

К счастью, нашлась небольшая методичка мехмата МГУ, где всё просто и понятно рассказано. Однородное диофантово уравнение в общей форме выражается так:

a⋅x + b⋅y = 0

То есть, у нас

a = 4⋅TPQN
b = -T

Не растягивая хронометраж статьи, решение будет таким:

x = T / GCD(a,b)
y = 4⋅TPQN / GCD(a,b)

где GCD(a, b) — наибольший общий делитель (greatest common divisor, GCD) a и b.

Ничего сложного

Посмотрим, где я свернул не туда. Вернёмся к уравнению

x/y = T/(4⋅TPQN)

Что здесь видит нормальный человек? Мы ищем x/y, и нам сразу же написан ответ: T/(4⋅TPQN). Иначе говоря,

x = T
y = 4⋅TPQN

Остаётся лишь сократить дробь до упора. То есть, поделить x и y на GCD(T,4⋅TPQN). На 100% тот же ответ, но получен на 1000% проще. Что ж, все мы иногда подвержены беспричинному усложнению.

Программа на C#, выполняющая манипуляции выше, чрезвычайно проста:

private static (long x, long y) MidiToMusical(long t, short tpqn)
{
    var gcd = GreatestCommonDivisor(t, 4 * tpqn);
    return (t / gcd, 4 * tpqn / gcd);
}

private static long GreatestCommonDivisor(long a, long b)
{
    while (b != 0)
    {
        var remainder = a % b;
        a = b;
        b = remainder;
    }

    return a;
}

Две строчки основного кода, опирающегося на вычисление наибольшего общего делителя алгоритмом Евклида. Осталось только убедиться в корректности вычислений:

const short tpqn = 100;

void TestMidiToMusical(long t)
{
    var (x, y) = MidiToMusical(t, tpqn);
    Console.WriteLine($"{t} ticks = {x}/{y}");
}

TestMidiToMusical(100);
TestMidiToMusical(200);
TestMidiToMusical(50);
TestMidiToMusical(400);
TestMidiToMusical(600);
TestMidiToMusical(20);

Мы будем использовать TPQN = 100, т.е. 100 тиков соответствует четвертной (1/4) длительности. Вывод программы корректен:

100 ticks = 1/4
200 ticks = 1/2
50 ticks = 1/8
400 ticks = 1/1
600 ticks = 3/2
20 ticks = 1/20

Ну и любопытства ради проверим какое-нибудь нелепое число тиков:

TestMidiToMusical(12345);

Вывод:

12345 ticks = 2469/80

И правда, 1/80 это 20-ая часть четвертной длительности, т.е. 5 тиков, а поделив 12345 на 5, получим числитель показанной дроби — 2469.

Музыкальное время в MIDI

Преобразование из музыкального времени x/y обратно в MIDI-тики T непозволительно простое. Возвращаясь к пропорции

x/y = T/(4⋅TPQN)

получаем

T = 4⋅TPQN⋅x / y

Выражая это в коде:

private static long MusicalToMidi(long x, long y, short tpqn) =>
    (long)Math.Round(4.0 * tpqn * x / y);

И снова проверки:

const short tpqn = 100;

void TestMusicalToMidi(long x, long y)
{
    var t = MusicalToMidi(x, y, tpqn);
    Console.WriteLine($"{x}/{y} = {t} ticks");
}

TestMusicalToMidi(1, 4);
TestMusicalToMidi(1, 2);
TestMusicalToMidi(1, 8);
TestMusicalToMidi(1, 1);
TestMusicalToMidi(3, 2);
TestMusicalToMidi(1, 20);
TestMusicalToMidi(2469, 80);

Здесь мы используем дроби, полученные в предыдущих тестах, ожидая вернуться к числам, переданным в TestMidiToMusical выше:

1/4 = 100 ticks
1/2 = 200 ticks
1/8 = 50 ticks
1/1 = 400 ticks
3/2 = 600 ticks
1/20 = 20 ticks
2469/80 = 12345 ticks

Идеально. Но есть нюанс. О нём я уже рассказывал в предыдущей статье, искать по слову “фокус”. Фокус состоит в использовании Math.Round. Пока музыкальные времена не образуют бесконечные десятичные дроби, всё в порядке. Но посмотрим, например, на 1/3:

TestMusicalToMidi(1, 3);

В тиках, согласно нашему алгоритму, такая дробь выражается числом 133. Теперь выполним обратное преобразование:

TestMidiToMusical(133);

Ответом будет 133/400, почти 1/3, но всё же не то.

Некоторые могут возразить, что таких нелепых длительностей не увидеть на реальных нотных листах. Скорее всего, да. При этом есть совершенно легитимные музыкальные записи особых ритмических делений (триоли, квинтоли, как-это-играть-оли и т.п.), позволяющие выразить своё творчество вот так:

Выделенные красным ноты имеют длительность как раз 1/3 (три ноты в пространстве одной целой). Думаю, для различного сорта авангардной музыки, когда исполнители не в силах сыграть в точности то, что они задумывали, такие вещи являются совершенной обыденностью.

К слову, пока я искал, как же может называться музыка с такими странными длительностями, набрёл на статью Неправильная музыка. Внезапно, речь там не о музыке, а о способе установки пушек на немецких истребителях Второй мировой. Английская версия, как водится, намного детальнее.

Заключение

Этой статьёй мы закрыли тему конвертации MIDI-времени в различные человеческие формы. Справедливости ради, существуют и другие способы представить время, например, SMPTE timecode. Но такие форматы редки и узкоспециализированы. Лично я ни разу не получал обращений касательно других представлений времени от пользователей моей библиотеки DryWetMIDI.

Предыдущие статьи:

• MIDI → Метр → MIDI

• Конвертация MIDI-времени в такты и доли