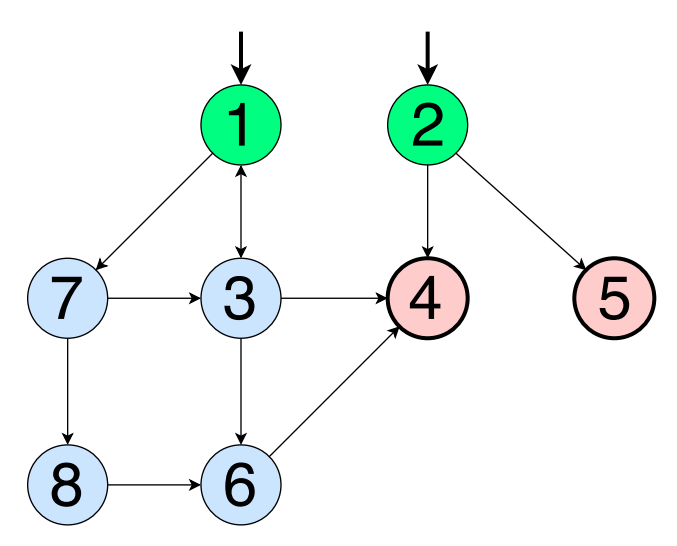
Большинство программ и алгоритмов можно представить в виде графа, состоящего из набора вершин (N) и ребер (Е). Покрытие графов в тестировании полезно тем, что можно проектировать тесты, используя разные критерии покрытия, и выявить ошибки. Что касается тестирования черного ящика, то покрытие графов здесь тоже может иметь большое значение, если приходится работать с состояниями и переходами, графами состояний сущности и т.д. Если граф достаточно сложен, разные критерии покрытия позволят оценить достаточность тестового набора.

В первой части: определения, покрытие вершин, ребер, путей, цикломатическая сложность.

Определения: основные пути

• Простой путь — это путь, где никакая вершина не появляется более одного раза, кроме начальной и конечной (которые могут совпадать). Простые пути не имеют внутренних циклов. Простой путь максимальной длины называют основным.
• Основной путь — это простой путь, не являющийся отрезком никакого другого простого пути. Перефразируем для ясности: основной путь не имеет внутренних циклов (вершины уникальны), и он самый длинный среди аналогичных путей. Если его можно сделать длиннее, тогда он является отрезком другого простого пути, а значит, не будет основным. (Оказывается, это очень простое понятие, как только вы его осознаете.)
• Например, рассмотрим путь [1, 2, 3, 4, 5, 6, 1] (не относящийся ни к одному из графов в этой статье). Это простой путь, поскольку все его вершины уникальны, кроме первой и последней. Исходя из предположения, что этот путь — не отрезок какого-либо другого, он будет также основным. С другой стороны, путь [1, 2, 3, 4] никак не может быть основным, поскольку мы знаем, что существует [1, 2, 3, 4, 5, 6, 1], и [1, 2, 3, 4] — определенно его отрезок. И значит, не основной.
• Замкнутый путь — основной путь ненулевой длины, который начинается и заканчивается в одной и той же вершине. [1, 2, 3, 4, 5, 6, 1] — простой путь, который также является основным и замкнутым.

Покрытие основных путей (ПОП)

Требования для тестового покрытия содержат все основные пути в графе G.

Простых путей в графе гораздо меньше, чем основных. Поэтому покрытие всех основных путей в графе — хороший способ сократить общее количество путей, которые стоит рассматривать. Количество тестовых путей сокращается без необходимости полагаться на субъективные суждения тестировщика, как в покрытии заданных путей, и требования не будут вычислительно-трудоемкими, как в полном покрытии путей.

Подход прост: определите набор основных путей и подготовьте тест-кейсы, реализующие каждый из них.

Покрытие основных путей включает покрытие вершин, ребер и попарное покрытие ребер. Согласно некоторым источникам ПОП не включает попарное покрытие ребер. Приводятся такие аргументы: если в вершине n есть ребро, исходящее из нее и входящее в нее же, это создаст следующее требование для попарного покрытия ребер: [n, n, m], где m — приемник n. Поскольку [n, n, m], очевидно, не основной путь, покрытие основных путей не может содержать этот путь, что в свою очередь означает, что покрытие основных путей не включает попарное покрытие ребер. Эта логика не совсем верна, поскольку тестовые требования для попарного покрытия ребер включают не [n, n, m], а [n, n], что, в свою очередь, абсолютно корректный основной путь.

требования = {
[1, 2, 6],
[1, 2, 3, 4, 6],
[1, 2, 3, 4, 5],
[2, 3, 4, 5, 2],
[3, 4, 5, 2, 3],
[4, 5, 2, 3, 4],
[5, 2, 3, 4, 5],
}
путь(T) = {
[1, 2, 6],
[1, 2, 3, 4, 6],
[1, 2, 3, 4, 5, 2, 3, 4, 5, 2, 6]
}

Причина, по которой последний тестовый путь несколько длиннее, такова: нам нужно пройти по циклу не один раз, а дважды, чтобы покрыть все требования.

Поиск основных путей

Для того, чтобы покрыть основные пути, нужно сначала все их найти. Самый легкий путь это сделать — начать с перечисления самых длинных путей в графе.



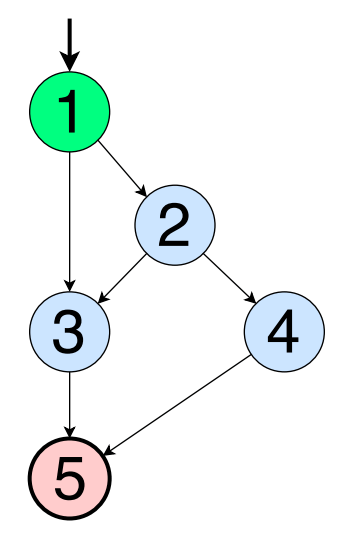
Используя граф из примера выше, начнем с перечисления самых длинных путей.

[1, 2, 3, 5]
[1, 2, 4, 5]

По определению основной путь — это простой путь, не являющийся отрезком другого пути. В общем случае в графе есть основные пути короче самых длинных. Эти пути «спрятаны» внутри циклов (подробности ниже), но в случае графа выше последний основной путь — прямой [1, 3, 5]. Все остальные пути, например, [2, 3, 5], отрезки уже перечисленных путей. Полный набор основных путей такой:

[1, 2, 3, 5]
[1, 2, 4, 5]
[1, 3, 5]

Как упоминалось выше, основные пути «прячутся» внутри циклов. Если в цикле x вершин, будет x дополнительных основных путей.



Если бы мы использовали метод, который применяли до этого, то получили бы следующие основные пути:

[1, 2, 3, 4, 6]
[1, 2, 6]
[1, 2, 3, 4, 5]

Начиная с вершины 2, мы обходим цикл один раз и возвращаемся в вершину 2. Так получается первый основной путь. Начиная с вершины 3, мы обходим цикл снова, возвращаясь в нее же. Так получается второй основной путь. Если мы повторим то же для вершин 4 и 5, мы получим 4 дополнительных основных пути. Сравните их с теми, что уже перечислены выше, и вы увидите, что это абсолютно новые основные пути (т.е. они не являются отрезками ни одного из перечисленных выше). Основные пути, которые начинаются и заканчиваются в одной и той же вершине, называются замкнутыми.

[2, 3, 4, 5, 2]
[3, 4, 5, 2, 3]
[4, 5, 2, 3, 4]
[5, 2, 3, 4, 5]

Теперь, когда мы познакомились с основными и замкнутыми путями, можно поговорить еще о некоторых критериях.

Простое покрытие замкнутых путей (ПрПЗП)

Требования для ПрПЗП содержат как минимум один замкнутый путь для любой достижимой вершины в G, которая начинает и заканчивает замкнутый путь.

Проще говоря, это означает, что среди всех замкнутых путей перечисленных выше, мы берем по одному для каждого цикла. Если в графе будет еще один цикл, нужно будет еще взять замкнутый путь, который покрывает вершины этого цикла, чтобы удовлетворить условия ПрПЗП.

В качестве примера снова рассмотрим граф из предыдущего раздела.

требования = {[2, 3, 4, 5, 2]}
путь(T) = {[1, 2, 3, 4, 5, 2, 6]}

ПрПЗП требует только один замкнутый путь для каждого цикла, если все вершины во всех замкнутых путях покрыты.

Полное покрытие замкнутых путей (ППЗП)

Аналогично ПрПЗП, но включает все замкнутые пути.

Требования содержат все замкнутые пути для каждой достижимой вершины в графе.

требования = {
[2, 3, 4, 5, 2],
[3, 4, 5, 2, 3],
[4, 5, 2, 3, 4],
[5, 2, 3, 4, 5]
}
путь(T) = {
[1, 2, 3, 4, 5, 2, 3, 4, 5, 2, 6]
}

Мы включили все замкнутые пути в покрытие, как того требует ППЗП. Если вы еще не заметили, важно осознавать, что ППЗП и ПрПЗП обладают странным свойством пропускать вершины и ребра графа, не входящие в замкнутые пути. Это значит, что они не включают попарное покрытие ребер, покрытие ребер или вершин. Посмотрите на иллюстрацию включений ниже.