Главная
«Сферический трейдер в вакууме»: инструкция по применению

«Сферический трейдер в вакууме»: инструкция по применению +11

14.10.2016 09:54

JamaGava 85 10600 Источник

Если проанализировать

форумов о рынках (в том числе Форекс), можно выделить два достаточно устойчивых мнения, назовём их пессимистическим и оптимистическим:

Пессимисты утверждают: рынок случаен «потому что я построил график случайного процесса и мой друг (профессиональный трейдер) не смог отличить его от графика EURUSD», а значит иметь стабильный доход на рынке( на Форекс) невозможно по определению!

Оптимисты им возражают: если бы рынок был случаен, котировки не гуляли бы в окрестности 1, а ушли в бесконечность. Значит рынок неслучаен и на нём можно зарабатывать. Я видел реально стабильно зарабатывающую стратегию с большим профит-фактором (больше стольки-то)!

Попробуем остаться реалистами и извлечь пользу из обоих мнений: предположим, что рынок случаен, и на основании этого предположения построим методику проверки доходности торговой системы на неслучайность.

Рассматриваемые в статье методики универсальны для любых рынков, будь то фонд, Форекс или любой другой!

Постановка задачи

Благодаря известному анекдоту про сферического коня в вакууме родилась замечательная аллегория, означающая идеальную, но совершенно неприменимую на практике модель.

Тем не менее, при правильной постановке задачи можно извлечь вполне ощутимую практическую пользу, применяя «сферическую модель в вакууме». Например, через отрицание «сферичности» реального объекта исследования.

Предположим, что у нас есть торговая система, используемая на некотором рынке. Также предположим, что рынок не случаен и система использует для принятия торговых решений что-то не являющееся замаскированным под индикаторы генератором случайных чисел. Для оценки стабильности дохода используем профит-фактор: $PF={P \over L}$ , где

— сумма дохода, а

— сумма убытка (положительное число).

Каким должен быть профит-фактор, чтобы можно было говорить о стабильности данной системы? Очевидно, что чем профит-фактор выше, тем больше поводов доверять системе. А вот нижняя граница оценивается разными специалистами по разному. Наиболее популярные варианты: > 2 (так себе), > 5 (хорошая система), > 10 (отличная система). Ещё встречается такая вариация: $PF_m={P-p_m \over L}$ , где

— максимальное значение дохода по сделке, такая величина называется достоверным профит-фактором. Считается, что минимальное допустимое значение для достоверного профит-фактора 1,6.

Что меня всегда смущало в профит-факторе, так это то, что никак не учитывается динамика рынка и интенсивность торговли. Поэтому я предлагаю другой подход к оценке значимости профит-фактора, нежели сравнение с каким-то заданным априори значением: профит-фактор должен быть как можно выше, но не ниже, чем профит-фактор случайной системы на случайном рынке с аналогичной интенсивностью торговли и волатильностью соответственно (по сути, не ниже чем у «сферического трейдера» в «идеальном газе» или в «вакууме»).

Осталось только построить идеальную модель для сравнения.

«Сферический трейдер...»

Предположим, что мы рассматриваем некоторую случайную торговую систему («сферический трейдер»). Так как модель случайна, то торговые события наступают в случайные моменты времени, независимо от решений, принятых ранее. Направление сделок также случайно (с вероятностью 0,5 продажа либо покупка). Объём сделок предположим константой и без потери общности будем оценивать доход и убыток в пунктах.

Пусть средняя длительность сделки составляет

, а среднее время между закрытием двух последующих сделок

(не будем накладывать никаких ограничений на количество одновременно открытых сделок).

Также предположим, что мы будем иметь дело с Пуассоновыми потоками событий:

Длительность сделки

будет являться случайной величиной с экспоненциальным распределением:

$f(t)=\lambda_te^{-\lambda_tt}\ \ \ (1.1)$

где

.

Количество сделок

, совершённых за период времени

будет описываться распределением Пуассона:

$P_T(k)={{\left(\lambda_\tau T \right)}^k \over k!}e^{-\lambda_\tau T}\ \ \ (1.2)$

где

"… в вакууме"

Теперь рассмотрим идеальную среду обитания «сферического трейдера» — «вакуум», то есть полностью случайный рынок.

Предположим, что рынок описывается нормальным распределением изменения значений котировок

за период времени

$f(\Delta)={1 \over \sigma_T \sqrt{2 \pi}}e^{\Delta^2 \over {2 \sigma_T^2}}\ \ \ (2.1)$

где

определяется следующим образом: пусть за единичное время котировки меняются на нормально распределённую случайную величину с дисперсией

, тогда, если рассматривать интервалы времени

, по изменения котировок будет иметь дисперсию:

$\sigma_T^2=\sigma_1^2 T\ \ \ (2.2)$

Это известное соотношение для Броуновского процесса.

С учётом формул (2.1) и (1.1) результат сделки, рассматриваемый как изменение котировок за период времени с начала до конца сделки будет описываться как интеграл условной вероятности

по

$f_{\sigma_1,\lambda_t}(\Delta)=\int\limits_{0}^{\infty} {\lambda_t \over {\sigma_1 \sqrt{2 \pi t}}}e^{-{\Delta^2 \over {2 \sigma_1^2 t}}}e^{-\lambda_tt}dt$

или

$f_{\sigma_1,\lambda_t}(\Delta)={\lambda_t \over {\sigma_1 \sqrt{2 \pi}}}\int\limits_{0}^{\infty} t^{-{1 \over 2}}e^{-{\Delta^2 \over {2 \sigma_1^2 t}}}e^{-\lambda_tt}dt\ \ \ (2.3)$

Решение этого интеграла с использованием Wolfram Mathematica даёт следующий результат:

$f_{\sigma_1,\lambda_t}(\Delta)={1 \over \sqrt{2}}{\sqrt{\lambda_t} \over \sigma_1}e^{-\sqrt{2} {\sqrt{\lambda_t} \over \sigma_1}|\Delta|}$

или

$f_{\sigma_1,\lambda_t}(\Delta)={\alpha \over 2}e^{-\alpha|\Delta|}\ \ \ (2.4)$

где $\alpha={\sqrt{2 \lambda_t} \over \sigma_1}$ .

Полученная закономерность является распределением Лапласа.

Таким образом, доход или убыток по одной сделке случайной системы на случайном рынке описывается распределением Лапласа, а абсолютная величина результата

сделки имеет экспоненциальное распределение:

$f_\alpha(R)=\alpha e^{-\alpha R}\ \ \ (2.5)$

где $\alpha={\sqrt{2 \lambda_t} \over \sigma_1}$ .

Известно, что экспоненциальное распределение является частным случаем распределения хи-квадрат (

при

). Это значит, что суммарный доход и суммарные потери могут описываться как суммы случайных величин с распределением хи-квадрат, а значит сами являются хи-квадрат величинами.

Пусть было совершено

прибыльных сделок с результами

убыточных с абсолютными значениями потерь

. Тогда суммарный доход

(нормированный на

) и суммарные потери

(также нормированные на

) будут описываться распределениями хи-квадрат со степенями свободы

соответственно:

$f\left(P_\alpha \right)=\chi_{k_p}^2\left({P_\alpha\right)\ \ \ (2.6)$

$f\left(L_\alpha \right)=\chi_{k_l}^2\left({L_\alpha\right)\ \ \ (2.7)$

где $P_\alpha={1 \over {2\alpha}}\sum\limits_{i=1}^{k_p}R_i^+$ и $L_\alpha={1 \over {2\alpha}}\sum\limits_{i=1}^{k_l}R_i^-$ .

отношение этих величин будет выглядеть следующим образом:

${P_\alpha \over {L_\alpha}}={{{1 \over {2\alpha}}\sum\limits_{i=1}^{k_p}R_i^+}\over {{1 \over {2\alpha}}\sum\limits_{i=1}^{k_l}R_i^-}}={{\sum\limits_{i=1}^{k_p}R_i^+} \over {\sum\limits_{i=1}^{k_l}R_i^-}}={P \over L}=PF\ \ \ (2.8)$

где $P=\sum\limits_{i=1}^{k_p}R_i^+$ суммарный доход, а $L=\sum\limits_{i=1}^{k_l}R_i^-$ суммарные потери. Их отношение

— профит-фактор.

Теперь рассмотрим следующую величину:

$PF_k=PF\times{k_l\over {k_p}}\ \ \ (2.9)$

Эту величину можно интерпретировать как «нормированный профит-фактор»: отношение среднего дохода к среднему убытку за сделку. Посмотрим, какое распределение имеет эта величина:

$PF_k=PF\times{k_l\over {k_p}}={P \over L}\times{k_l\over {k_p}}={{P_\alpha} \over {L_\alpha}}\times{k_l\over {k_p}}={{{P_\alpha} \over {2k_p}}\over{{L_\alpha} \over {2k_l}}}\ \ \ (2.10)$

Полученная величина, отношение хи-квадрат величин, нормированных на количества их степеней свободы, — имеет распределение Фишера.

Таким образом, мы нашли распределение величины, статистики

для профит-фактора «сферического трейдера в вакууме» при известном количестве прибыльных

и убыточных

сделок.

Прежде чем переходить к обобщению на случай неизвестных

, рассмотрим поведение «сферического трейдера» на «не совсем случайном» рынке (назовём эту среду в шутку «идеальным газом»).

"… в идеальном газе"

Теперь рассмотрим чуть более сложную ситуацию: когда рынок является обобщённым броуновским движением. То есть, в отличие от случайного, обладает памятью. В этом случае формула (2.2) примет следующий вид:

$\sigma_T^2=\sigma_1^2 T^{2H}\ \ \ (3.1)$

где

— показатель Хёрста, величина, характеризующая фрактальные свойства временного ряда и связанная с фрактальной размерностью Хаусдорфа-Безиковича

следующим образом:

. Показатель Хёрста может принимать значения

.

При

временной ряд вырождается в случайный, не обладающий памятью, соответсвует рассмотренному выше случаю. При

ряд постоянно стремится к изменению направления существующей тенденции, а значит обладает памятью, такой ряд называется антиперсистентным, хаотическим. При

ряд также обладает памятью, но стремится к сохранению существующей тенденции, такой ряд называется персистентным, детерминированным. Чем сильнее показатель Хёрста отличен от 0.5, тем чётче у ряда выражены хаотические или детерминированные свойства.

Для различных рынков характерны различные значения показателя Хёрста, кроме того, они могут меняться со времен. Показатель Хёрста может быть рассчитан по значениям временного ряда. А значит, при оценке профит-фактора можно учесть величину

, рассчитанную по ряду котировок в тот же период, когда совершались сделки анализируемой стратегии. Для оценки показателя Хёрста существует несколько стандартных процедур, например RS-статистика или методы основанные на вейвлетах.

Предположим, что случайная торговая стратегия работает на рынке с показателем Хёрста H, тогда с учётом (3.1), формула (2.3) примет вид:

$f_{\sigma_1,\lambda_t,H}(\Delta)={\lambda_t \over {\sigma_1 \sqrt{2 \pi}}}\int\limits_{0}^{\infty} t^{-H}e^{-{\Delta^2 \over {2 \sigma_1^2 t^{2H}}}}e^{-\lambda_tt}dt\ \ \ (3.2)$

Очевидно, что при

это выражение эквивалентно (2.3).

К сожалению, выражение (3.2) в аналитическом виде не интегрируется. Поэтому, для нахождения распределения абсолютных значений разностей котировок между моментами времени начала и конца сделки (абсолютных итогов сделок) при случайной торговле на рынке с показателем Хёрста

мы воспользуемся численным моделированием.

Я проводил моделирование с использованием Python.

Моделирование проводится следующим образом

1) Задаём параметры моделирования:

— объём экспериментальной выборки;

— количество диапазонов для построения гистограммы

2) Генерируем выборку distE экспоненциально распределённой случайной величины и выборку distN нормально распределённой величины объёмом N каждая.

3) Учитывая соотношение (3.1), создаём тестовую выборку distT, каждое значение которой рассчитывается из соответствующих значений distN и distE:

4) Для полученного распределения строится гистограмма из M диапазонов (количество попаданий в диапазоны). Из полученной гистограммы выбирается K первых диапазонов, количество попаданий в которые отлично от нуля. Также производится нормирование на количество попаданий в первый диапазон.

5) На основании полученной гистограммы аппроксимируется вид распределения.

import matplotlib.pyplot as plt
import numpy as np
from scipy import stats

def testH(N, M, H, p):
    distE = np.random.exponential(1, N)
    distN = np.random.normal(0, 1, N)
    
    distT = abs(distN * distE**H)
    
    if p == 1:
        plt.figure(1)
        plt.hist(distT, M)
        plt.title('H='+str(H))
    
    [y, x] = np.histogram(distT, M)
    
    K = 0;
    for i in range(M):
        if y[i] > 0:
            K = i
        else:
            break  
    
    y = y * 1.0 / y[0]
    x = x[1:K]
    y = y[1:K]
    
    return getCoeff(x, y, p, 'H='+str(H))

Примеры гистограмм полученных распределений для значений показателя Хёрста 0.1, 0.3, 0.5, 0.7 и 0.9 приведены ниже.

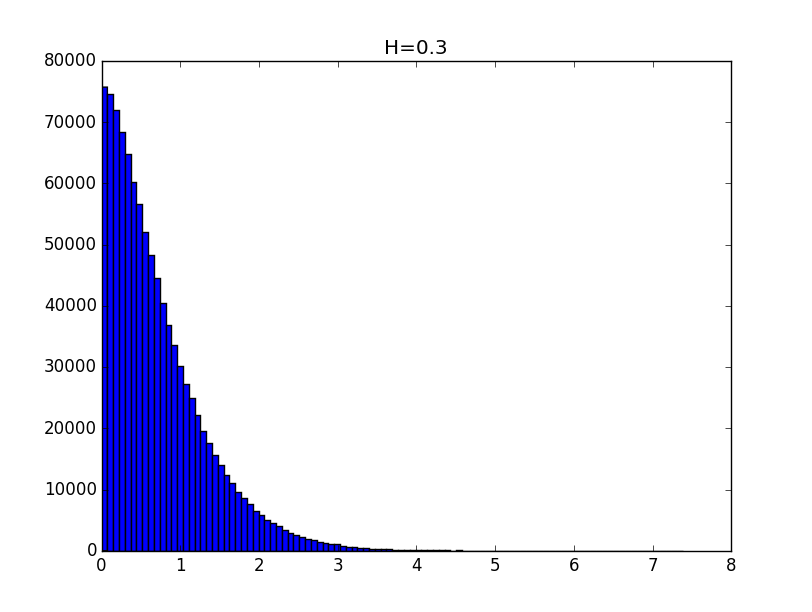
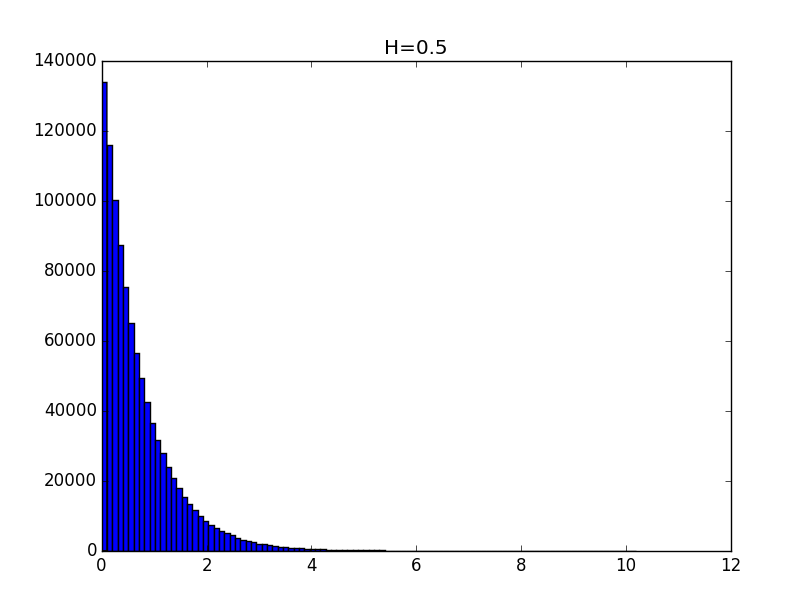
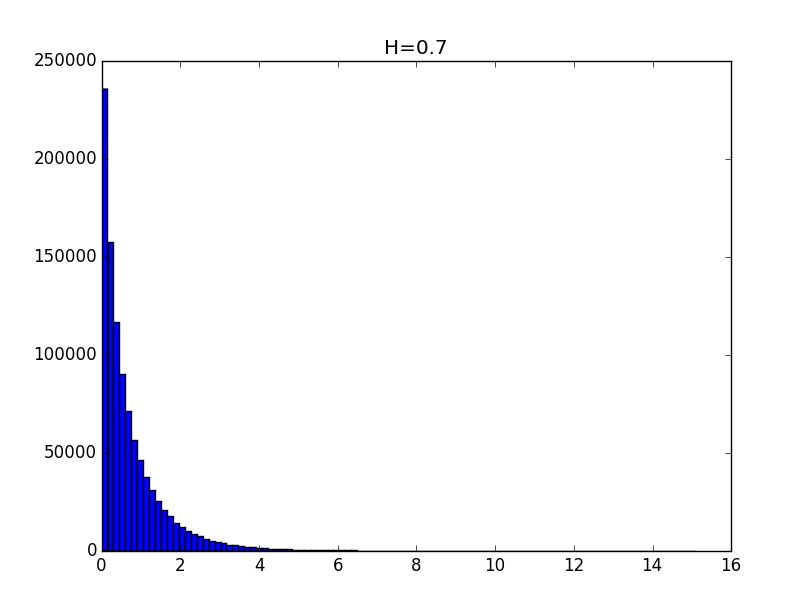
Общий вид гистограмм даёт основание предположить, что полученные распределения с точностью до константы могут описываться функцией вида:

$f_{\sigma_1,\lambda_t,H}(\Delta)=Ce^{-\Delta^{K_{\sigma_1,\lambda_t,H}}}\ \ \ (3.3)$

Для поиска параметро распределения воспользуемся следующим алгоритмом:

1) Пусть нам даны

— центроиды диапазонов гистограммы и

— количества попаданий в диапазоны, нормированные на количество попадание в первый диапазон.

2) Тогда, игнорируя первый диапазон, выполним преобразования:

3) Воспользовавшись методом наименьших квадратов, найдём параметры линейной регрессии

такие, что

4) На основании полученного

принимаем:

.

Параметр

компенсирует погрешность нормировки.

Листинг процедуры, выполняющей расчёт коэффициентов приведён ниже:

def getCoeff(x, y, p, S):
    X = np.log(x)
    Y = np.log(-np.log(y))
    n = len(X)
    
    k = (sum(X) * sum(Y) - n * sum(X * Y)) / (sum(X) ** 2 - n * sum(X ** 2))
    b = (sum(Y) - k * sum(X)) / n
    if p == 1:
        plt.figure(2)
        plt.plot(np.exp(X), np.exp(-np.exp(Y)), 'b', np.exp(X), np.exp(-np.exp(k * X + b)), 'r')
        plt.title(S)
        
        plt.show()
        
    return k

Ниже приводятся примеры для огибающих гистограмм для значений показателя Хёрста 0.1, 0.3, 0.5, 0.7 и 0.9 (синяя линия) и их модели (красная линия):

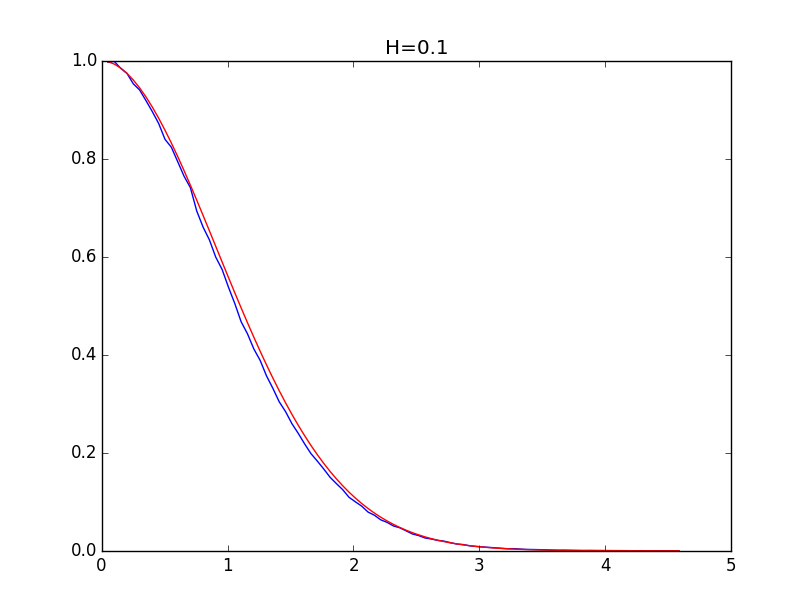
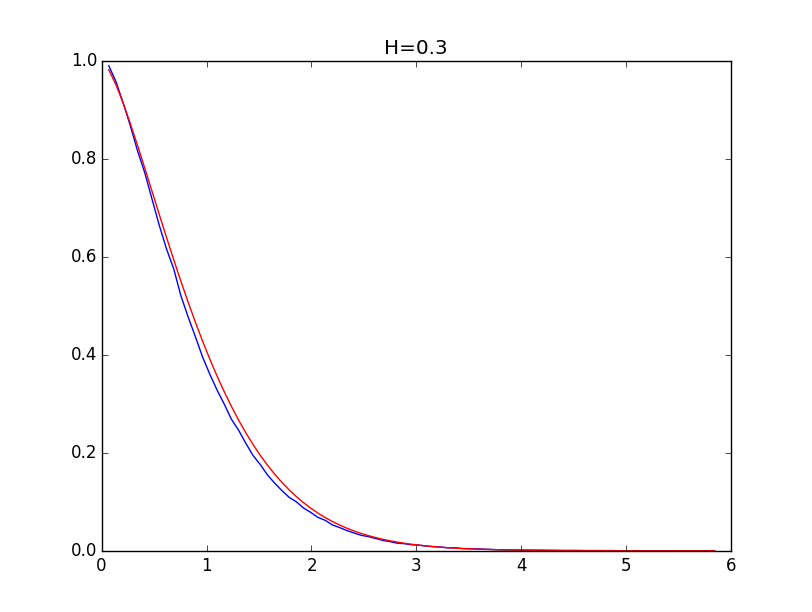
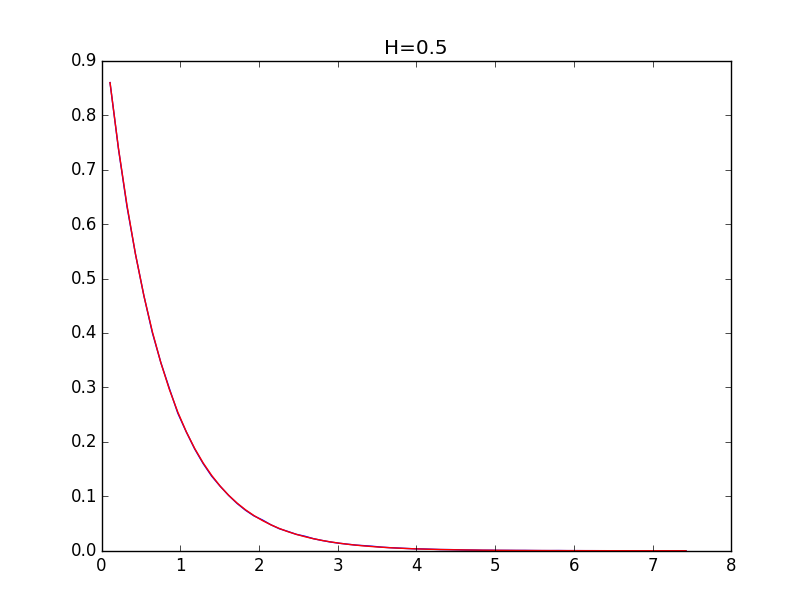
При значениях показателя Хёрста выше 0.5 точность моделирования выше.

Теперь найдём зависимость

от

. Для этого смоделируем ряд значений

для различных

и попробуем установить функциональную зависимость.

Я использовал для моделирования значения

от 0.01 до 0.99 с шагом 0.01. При этом, для каждого значения

значения

вычислялись 20 раз и усреднялись:

if __name__ == "__main__":

    N = 1000000;  
    M = 100; 
    
    Z = np.zeros((99, 2))
    
    for i in range(99):
        Z[i, 0] = (i + 1) * 0.01
        
        for j in range(20):
            W = float('nan')
            while np.isnan(W):
                W = testH(N, M, (i + 1) * 0.01, 0)
            Z[i, 1] += W
            
        Z[i, 1] *= 0.05
        print Z[i, :]
                
    X = Z[:, 0].T
    Y = Z[:, 1].T

    plt.figure(1)
    plt.plot(X, Y)
     
    plt.show()

Полученная зависимость имеет следующий вид:

График похож на искажённый сигмоид, поэтому и закономерность будем искать в виде сигмоида:

$K(H)=d - {c \over b + e^{a_3 H^3 + a_2 H^2 + a_1 H + a_0}}\ \ \ (3.4)$

Проведение численной процедуры минимизации методом наименьших квадратов даёт следующие результаты:

Суммарная квадратичная ошибка составляет порядка 0.005.

Ниже приведёны графики экспериментальной зависимости

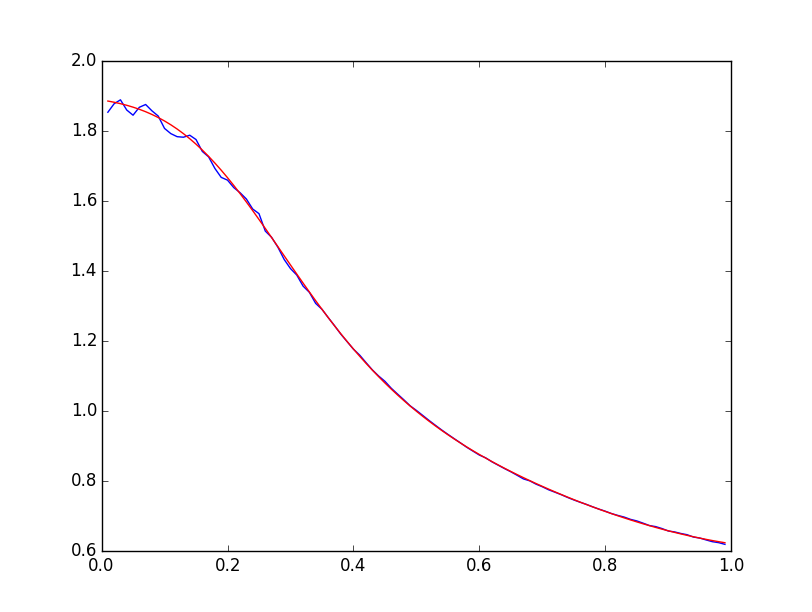
(синяя линия) и модельной по формуле (3.4) (красная линия):

Следует отметить, что полученная закономерность справедлива лишь для случая, когда

. Поэтому в дальнейшем будем полагать эти условия выполняющимися (обеспечим их выполнение) и опустим соответствующие индексы.

Теперь, учитывая (3.3) и (3.4) для оцененного значения

мы знаем распределение абсолютного значения сделок. Используя свойство распределения преобразования случайной величины, произведём замену переменной в (3.4):

Тогда:

$f_{H}(\Delta)=Ce^{-\Delta^{K(H)}} >>> f'_{H}(\delta)={C \over K}\delta^{{1 \over {K(H)}}-1}e^{-\delta}\ \ \ (3.6)$

Это функция плотности вероятности величины, имеющей гамма-распределение с количеством степеней свободы

и единичным параметром масштаба. Учитывая это, формула (3.6). Должна быть переписана как:

$f'_{H}(\delta)={1 \over {\Gamma\left({1 \over {K(H)}}\right)}}\delta^{{1 \over {K(H)}}-1}e^{-\delta}\ \ (3.7)$

Подведём промежуточный итог:

Имея информацию о показателе Хёрста рынка

, рассчитанном для того же периода истории, на котором мы тестируем систему, мы можем найти величину

используя формулу (3.4). Также мы можем найти среднюю интенсивность торговли

и параметр

для результатов сделок. Для того, чтобы предложенные выше формулы были справедливы, необходимо привести значения

к единице. Для этого выполним нормировку:

, где

— результат

сделки (независимо от знака результата). Это преобразование следует из (3.1).

Согласно (3.7), величины

будут иметь гамма-распределения с параметрами

. Следовательно, величины

будут иметь распределение хи-квадрат c

степенями свободы.

Пусть было совершено

прибыльных сделок со значениями дохода

с величинами убытка

(положительные значения). Тогда, с учётом

и (3.7), величины

$P_H=2\sum \limits_{i=1}^{k_P}{(R_i^+)}^{K(H)}$

и

$L_H=2\sum \limits_{i=1}^{k_L}{(R_i^-)}^{K(H)}$

будут иметь хи-квадрат распределения с количествами степеней свободы

соответственно.

Следовательно, величина:

$PF_H={P_H\over{L_H}}\times{k_L\over {k_P}}={{\sum \limits_{i=1}^{k_P}{(R_i^+)}^{K(H)}}\over{\sum \limits_{i=1}^{k_L}{(R_i^-)}^{K(H)}}}\times{k_L\over {k_P}}\ \ \ (3.8)$

будет иметь распределение Фишера c

степенями свободы (количество степеней свободы, в общем случае, будет нецелым, таким образом проявляются фрактальные свойства рынка).

Назовём величину

обобщённым нормированным профит-фактором. При

обобщённый профит-фактор вырождается в привычный нам нормированный профит-фактор (2.9).

Окончательное обобщение

Итак, мы исследовали «сферического трейдера» на случайном рынке и нашли распределение нормированного профит-фактора. Затем обобщили результаты на случай рынка с произвольной фрактальной размерностью, представленной измеримой величиной — показателем Хёрста.

Теперь у нас есть величина, которую мы назвали обобщённым нормированным профит-фактором, который вычисляется с использованием информации о результатах сделок (не забудем, кстати, скорректировать их с учётом спреда: отнять его от убытков и прибавить к доходам). Для большей универсальности методики, объём сделок считаем постоянным, либо измеряем всё в пунктах. Не забываем также проводить нормировку на среднюю длительность сделки и стандартное отклонение распределения результатов сделок:

, где

— результат

сделки.

Все полученные на данный момент результаты завязаны на известное количество прибыльных и убыточных сделок, которое является случайной величиной с биномиальным распределением для известного общего количества сделок, которое, в свою очередь, также случайная величина, распределённая по Пуассону.

Введем новое обозначение. Пусть обобщённый нормированный профит-фактор (3.8) для заданного количества прибыльных

и количества убыточных

сделок (при известном показателе Хёрста

) обозначается как

и имеет распределение Фишера со степенями свободы

.

Тогда, с учётом биномиального распределения количества прибыльных и убыточных сделок, а также равновероятности получения дохода либо убытка на каждой сделке введём величину

— обобщённый нормированный профит-фактор, учитывающий лишь общее количество сделок. Эта величина будет иметь следующее распределение:

$F_N(PF_{H, N})=\left({1 \over 2}\right)^N\sum\limits_{k=0}^{N}{\left[{N!\over{k!(N-k)!}} F_{2kK(H),2(N-k)K(H)}(PF_{H, N})\right]}\ \ \ (4.1)$

где

— плотность распределения Фишера со степенями свободы

, а величина

описывается формулой (3.4), где

— показатель Хёрста.

На практике, при достаточно больших

выражение (4.1) может быть аппроксимировано неполной суммой:

$F_N(PF_{H, N})={\sum\limits_{k=a}^{b}{\left[{N!\over{k!(N-k)!}} F_{2kK(H),2(N-k)K(H)}(PF_{H, N})\right]} \over {\sum\limits_{k=a}^{b}{N!\over{k!(N-k)!}}}}\ \ \ (4.1*)$

где

(

) ограничивают некоторое подмножество возможных значений количества прибыльных сделок.

Теперь рассмотрим обобщённый нормированный профит-фактор без привязки к какому-либо количеству сделок, а лишь учитывающий среднюю интенсивность торговли

и период тестирования стратегии

. Учитывая, что общее количество сделок распределено по Пуассону,

будет иметь следующее распределение:

$PF_{\lambda_\tau,T,H}=\sum\limits_{k=0}^\infty {{\left(\lambda_\tau T\right)^k\over{k!}}F_k(PF_{H,N})}\ \ \ (4.2)$

Или, для рассматриваемого количества сделок в диапазоне

$PF_{\lambda_\tau,T,H}={\sum\limits_{k=a}^b {{\left(\lambda_\tau T\right)^k\over{k!}}F_k(PF_{H,N})} \over {\sum \limits _{k=a}^b{\left(\lambda_\tau T\right)^k\over{k!}}}}\ \ \ (4.2*)$

Полученное распределение может использоваться для проверки значимости рассчитанного по (3.8) обобщённого нормированного профит-фактора для торговой системы с известными средней длительностью сделки и интенивностью торговли за известное время работы на рынке с известными волатильностью и показателем Хёрста. Методика применения теста абсолютно аналогична таковой для теста Фишера. Для её проведения достаточно заменить в (4.1) (или в (4.1*)) функцию плотности на функию распределения Фишера и подставить в качестве аргумента значение рассчитанного обобщённого профит-фактора. Полученное значение вероятности необходимо сравнить с величиной

, где

— требуемый уровень значимости. При превышении этого уровня для рассчитанной статистики можно отвергать гипотезу о случайности торговой ситемы (о «сферичности трейдера в вакууме»).

Заключение

Предложенный в работе подход, основанный на построении обобщённого нормированного профит-фактора с учётом волатильности и фрактальных свойств рынка, а также интенсивности торговли и средней длительности сделок, позволяет построить статистический тест значимости достигнутых результатов с точки зрения вероятности получения аналогичных результатов случайным образом. Используя тест, можно с заданным уровнем значимости говорить о выполнении необходимого условия для констатации надёжности системы. Но полученные результаты не будут являться достаточным условием…

К сожалению, мне не известен тест, результатов которого будет достаточно для однозначного принятия стратегии как безусловно надёжной.

Поделиться с друзьями

-->

Комментарии (85)

norlin
14.10.2016 13:26
#9860002
+3
Случаен ли рынок? Можно ли стабильно зарабатывать на Форекс?
Сколько можно-то. Рынок не случаен, на нём можно зарабатывать. Форекс – не рынок, на нём можно играть (и, возможно, выигрывать), но не зарабатывать.
1. JamaGava
  14.10.2016 14:03
  #9860132
  Спасибо за Ваш комментарий.
  Я не берусь утверждать случаен рынок или нет, а предлагаю методику проверки стратегии исходя из модели "случайный рынок".
  Форекс — тоже рынок по определению: точка пересечения интересов продавцов и покупателей.
  Ваши утверждения по поводу неслучайности рынка и случайности Форекса, извините, голословны (по крайней мере, мне не встречались рынки с показателем Хёрста 0.5… и даже <0.5… хотя не отрицаю, что такие рынки или периоды истории возможны).
  Про мнения, схожие с Вашим, я как раз писал в самом начале статьи :)
  1. norlin
    14.10.2016 15:27
    #9860388
    +4
    Смысл Форекса – в игре с самой площадкой, а не в торговле с другими клиентами. В отличие от настоящих рынков ценных бумаг.
    
    felidae
    14.10.2016 17:53
    #9860720
    +1
    Вы путаете форекс как внебиржевой валютный рынок с кухнями, которые могут позволять торговать хоть ценными бумагами, но при этом выступать второй стороной сделки.
    При этом и обычные банки могут осуществлять внутренний клиринг вполне законно и без каких-то вопросов к ним. Да и кредитное плечо, являющееся чуть ли не самой главной проблемой для трейдеров-непрофессионалов, предоставляется в том числе и на биржах.
    
    jex
    14.10.2016 17:53
    #9860724
    -1
    Вы не ту биржу выбираете. На реальном форексе — торговля с клиентами
    
    JamaGava
    14.10.2016 17:57
    #9860732
    Как бы то ни было с честностью брокеров, в посте я предложил методику, которую можно применять не только к форексу, но и любому рынку…
    А можно даже то и к оценке системы прогноза погоды, если придумать систему поощрений и штрафов за верно/неверно спрогнозированное направление изменения температуры, влажности и т.д.
    
    JamaGava
    14.10.2016 18:44
    #9860836
    Теоретически предложенную мной методику сможет использовать даже сама "торговая площадка" для оценки стабильности своих доходов.
  1. JamaGava
    14.10.2016 18:46
    #9860840
    Фраза "Случаен ли рынок? Можно ли стабильно зарабатывать на Форекс?" предполагалась для привлечения внимания читателей… и уже удалена по причине провокационности :)
    
    Я не анализирую случайность форекса или или иного рынка. Я предлагаю методику проверки доходности системы.
  1. CountZero
    14.10.2016 20:57
    #9860982
    я не математик, но
    
    Оптимисты им возражают: если бы рынок был случаен, котировки не гуляли бы в окрестности 1, а ушли в бесконечность. Значит рынок неслучаен и на нём можно зарабатывать.
    
    бросаем кубик. выпадает число от одного до шести. по аналогии с рынком, если бы величина была случайная — она не гуляла бы в этих окрестностях, а ушла в бесконечность, получается так?
    хотя можно сказать, что рынок и идёт в бесконечность, вместе с инфляцией и НТР, только о-о-очень медленно, но S&P и ММБВ недавно на исторические хаи вышли.
    на мой обывательский взгляд, будущее случайно, если будущие события не предопределены прошлыми, а прошлое лишь может влиять на шансы (вероятности) их появления. на случайных процессах можно зарабатывать — например, игра в блэк-джек остаётся случайным процессом, тем не менее, считая карты, можно повышать вероятность выигрыша.
    на рынке (хоть он и случаен) тоже можно зарабатывать — например, правильно прогнозируя действия крупных игроков. это дивидендный трейдинг, сделки m&a, скальпинг. и находя ситуации, в которых вероятность получения прибыли значительно превышает вероятность получения убытка.
    
    JamaGava
    14.10.2016 23:14
    #9861132
    А я и не сторонник оптимистов, я предлагаю позицию реалистов: допускающую и случайность и детерминированность рынка и торговой системы.
    
    По поводу игральных костей — не совсем удачный пример, на мой взгляд… Лучше так: x=1. Затем бросаем монетку и прибавляем к х 0.0001, если решка или -0.0001 если орёл. Так делаем очень много раз… В итоге, как ни странно, вероятность обнаружить х=1 всё меньше.
    
    nanobiot
    17.10.2016 13:10
    #9863588
    Теорвер говорит совершенно противоположное.
    при достаточно большом числе подбрасываний правильной монеты, частота выпадения орла и решки стремится к 0,5, то есть вероятность обнаружить х=1 все больше. разве нет?
    
    JamaGava
    17.10.2016 14:04
    #9863718
    +1
    Количество выпадений орла и решки описывается биномиальным распределением. При большом количестве экспериментов в одной серии, распределение стремится к нормальному (как вследствие свойств биномиального распределения, так и согласно центральной предельной теореме) с дисперсией, пропорциональной количеству экспериментов, то есть, с большой дисперсией.
    А то о чём Вы говорите, касается оценки свойств распределения Бернулли — каждого отдельного эксперимента…
    
    Смотрите:
    Пример выше был адаптирован под предмет дискуссии — рынок. Сделаем проще, если "решка", то x<-x+1, если "орёл", x=x-1. До эксперимента x<-0.
    Пусть за подбрасываний монеты, с суммированием результата у нас получилось число . Предположим, это не нарушает общности рассуждений. О чём говорит это число? О том, что решка выпала раз. Эта величина подчиняется биномиальному распределению, а значит матожидание для равно , а дисперсия . То есть, говоря по простому, наибольшая вероятность для значений это интервал . Если мы захотим теперь проверить вероятность выпадения решки и разделим полученный результат на количество экспериментов, то получим величину в диапазоне , который, очевидно, сходится к при росте количества экспериментов. Полностью соответствует Вашим рассуждениям.
    
    Но вернёмся к значению . При выпадении решки раз: . И если как мы выяснили выше с большой вероятностью обнаруживается в диапазоне , то при этом будет обнаруживаться в диапазоне , который, как мы видим расширяется с ростом .
1. ittakir
  14.10.2016 16:55
  #9860600
  -3
  Чем же пара EURUSD на форексе отличается от какого-нибудь графика акций сбербанка?
  Вы ни там, ни там на движение цены своими сделками повлиять не можете. В обоих случаях есть какие-то разумные границы, куда график точно не уйдет в ближайшее время. В акциях весьма вероятен какой-нибудь инсайд, манипуляции. А попробуй сдвинуть EURUSD или золото…
  И у форекса есть преимущество — ты можешь торговать, имея на счете всего 100$ и стоя в пробке прямо с телефона 24 часа в сутки, без абонентской платы.
  Единственная притензия, которую бы я принял, это история вида «заработал на форексе 100500$, а вывести средства не дали». Но нет же. Теряют деньги, принимая неверные решения о сделках, а потом винят во всем «форекс-кухню».
  1. selenite
    14.10.2016 17:51
    #9860718
    +1
    Разумным аргументом будет то, что клиенту форекс-кухни отдается просто рандомный график непонятно чего, условно привязанный к курсу валюты. EURUSD? А золото, опционы, или там BTCUSD/пара bitcoin и dogecoin, не?
    
    При таких условиях нет абстракции «человек торгует на валютном рынке», есть «человек играет с псевдослучайным набором цифр».
    
    JamaGava
    14.10.2016 17:58
    #9860736
    Используя предложенную методику Вы как раз и сможете оценить степень случайности комплекса брокер+Ваша_система (правда, не сможете выделить виновника, если всё окажется случайным).
    
    ittakir
    14.10.2016 18:13
    #9860776
    +2
    Ну так сравните график на форексе с графиком того же инструмента где-нибудь еще (google, finviz, etc.). Если отличия и будут, то только на тиковом графике. Опасаетесь фейковых выбросов-иголок? Торгуйте без автоматических стопов на большом тайм-фрейме, скажем больше чем 5 мин. Стопы отрабатывайте вручную.
    Например, вы хотите заработать на колебаниях курса рубля. На форексе это можно сделать со спредом 1 копейка, а не 2 рубля, как в обменнике. Курс общедоступен. Торговать можно в любое время, сидя на унитазе с телефоном. Сегодня купил за 62, завтра продал за 62.40.
    Аргументируйте, почему форекс для этого не подойдет?
    
    LightSUN
    15.10.2016 14:20
    #9861564
    Опасаетесь фейковых выбросов-иголок? Торгуйте без автоматических стопов на большом тайм-фрейме, скажем больше чем 5 мин.
    
    На кухне вряд ли что-то поможет. Вот для примера фьючерсы USD/RUB до 12.16 на часах у «Открытия».
    
    Скрытый текст
    
    ittakir
    15.10.2016 16:03
    #9861658
    Кстати, не факт, что по ним сработают стопы на закрытие позиции. На открытие точно не срабатывают, т.е. купить доллар по 62.00 не получится (проверял лично).
    Ну и, как я уже сказал, торгуйте руками. Эти иголки — они одномоментные. Алготрейдинг тоже можно научить пропускать их, понимая, что график не может так резко изменяться.
    
    LightSUN
    15.10.2016 17:05
    #9861726
    Торговать руками или нет отдельный вопрос. Насколько мне известно сейчас большинство торгует роботами.
    Другой вопрос откуда эти иголки берутся если брокер не создаёт их специально. Если посмотреть на московскую биржу (тоже фьючерсы), то там такого нет (смотрю через альфа-директ). У открытия кстати для USD_TOM котировки не на 100% совпадают с официальными, что имхо уже намекает на «порядочность».
    
    sviterov
    14.10.2016 19:09
    #9860874
    BTCUSD, золото и пр. есть у многих серьезных форекс-брокеров, просто надо поискать
  1. CountZero
    14.10.2016 21:38
    #9861014
    поищите на хабре «itinvest форекс», там подробно всё расписано. торгуя суммой $100, у вас и плечо будет соответствующее, и результат вполне закономерный. возможностей заработать на фондовом рынке в сотни раз больше.
    
    ittakir
    15.10.2016 08:17
    #9861342
    Все верно, плечо 1:100. Но и купить можно 0.01 лота, так что эффективное плечо станет 1:1. Изменился курс на 5%, и ваша капитал изменится всего на 5% — все как в акциях.
  1. Daemon_Hell
    14.10.2016 22:51
    #9861092
    Из недавних примеров — фунт уронили на 6% ночью в азии. Большой объем? Не думаю.
    
    ittakir
    15.10.2016 08:24
    #9861344
    Ага, зато когда президент вдруг решит публично отчитать какого-нибудь главу Мечела, то акции летят вниз на 50%.
    Я не говорю, что валюта не может скакать. Просто в акциях это может происходить чаще и менее контролируемо.
1. sviterov
  14.10.2016 17:56
  #9860730
  +3
  Форекс – не рынок, на нём можно играть (и, возможно, выигрывать), но не зарабатывать.
  
  Конечно, котировки EURUSD ведь там совсем другие!
  На один и тот же график можно найти хоть 10 инструментов, в том числе форекс. И выбор инструмента на возможность правильного предсказания дальнейших событий влияет мало.
1. cepstrum
  14.10.2016 23:15
  #9861134
  Сколько можно-то. Рынок случаен. На нем нельзя зарабатывать, только играть. Форекс тоже рынок. :)
1. smxfem
  14.10.2016 23:15
  #9861136
  Форекс – не рынок, на нём можно играть (и, возможно, выигрывать), но не зарабатывать.
  
  Фо?рекс (Forex, иногда FX, от англ. FOReign EXchange — «зарубежный обмен») — рынок межбанковского обмена валюты по свободным ценам
  
  Попыток получить стабильно приносящую прибыль стратегию масса, и все провалились
  Из этого не следует, что такой стратегии не существует.
  Все равно что утверждать: вечного двигателя нет, потому что все попытки его создания провалились. Деда мороза нет, потому что все деды морозы которых видел оказались не настоящими. Или такого рода ошибки популярны: курильщики умирают в среднем раньше, чем не курящие, следовательно курение влияет на продолжительность жизни.
  Где логика? Причина же может быть, например, не курение, а некая третья сущность. Причиной может быть то, что выигрышную стратегию плохо искали, а не её отсутствие в принципе.
  Иногда ошибочная логика приводит к верному результату, но не всегда.

yury-dymov
14.10.2016 14:50
#9860314
+6
Я ничего не понял, но формулы и графики красивые.
1. JamaGava
  14.10.2016 17:59
  #9860740
  +1
  Спасибо.
  Если Вас заинтересовало и хотите разобраться в методике, готов пообщаться в личке.

Canep7
14.10.2016 17:59
#9860742
+1
Если целью статьи было доказательство неслучайности рынка, то все делается на порядок проще. В физике и статистике давно определены математические критерии случайных и неслучайных сигналов. В частности, авто корреляция случайного сигнала равна нулю и спектр случайного сигнала равномерный. Если это вычислить для рынка, то сразу видно, что никакой случайностью там особо и не пахнет, слишком много неслучайного.

К примеру, если получить спектр при помощи разложения в ряд Фурье для дискретных сигналов, то получим весьма выразительные пики на спектральной картине, что однозначно свидетельствует о наличии серьезных закономерностей в рыночных ценах.

И не придется городить весь этот огород с имитацией ТС, трейдера и т.п. слишком сложно, потому не очень убедительно, вероятность ошибки велика… а вот ряды Фурье — штука элементарная, ошибиться почти негде.
1. JamaGava
  14.10.2016 18:02
  #9860752
  Спасибо за комментарий.
  К сожалению, Вы не правильно поняли цель статьи.
  
  Я не доказываю ни случайность ни противоположное. Я предлагаю методику для оценки результатов торговой системы, прежде чем выпускать её на реальный счёт… Дабы потом не грешить на плохой случайный рынок или на жадного брокера.

fivehouse
14.10.2016 18:02
#9860754
+2
Еще чуть-чуть и вы отойдете от моделей рассматривающих случайность и начнете рассматривать стационарные и не стационарные временные ряды. Теории усточивости траекторий. А потом плавно перейдете к теории хаоса. Это обычный путь. Очень важно не потеряться в теории хаоса (многим это не удалось). И очень важно совершить этот переход за время существенно короче времени жизни. Удачи.
1. JamaGava
  14.10.2016 18:03
  #9860758
  Спасибо за комментарий.
  Теория хаоса действительно штука сложная.
  Для моих насущных задач пока хватает мат.статистики :)
1. SADKO
  15.10.2016 22:22
  #9862012
  Истинно такъ!

SurfCalavera
14.10.2016 18:04
#9860760
+1
Наиболее популярные варианты: > 2 (так себе), > 5 (хорошая система), > 10 (отличная система)

очень заинтересовали градации. либо я что-то не так понял, либо это ошибка.

за торговую систему выдающую в два раза больше доходов чем убытков трейдеры продадут свойу душу и душу соседа заодно. как-то не кажется что она классифицируется «так себе»
1. JamaGava
  14.10.2016 18:06
  #9860764
  Спасибо за комментарий.
  
  Градации почерпнуты с каких-то форумов, к сожалению, уже не помню источник. Возможно там речь шла о фонде.
  
  Идея статьи как раз в том, чтобы не сравнивать профит-фактор с каким-то "просто числом", а определить этот порог исходя из свойств рынка и торговой системы, используя аппарат мат.статистики и такую категорию как "уровень значимости теста".
  
  Кстати, эту провокационную цитату про "так себе"->"хорошо"->"отлично" я уже убрал, дабы не смущать народ :)
  1. SurfCalavera
    14.10.2016 18:15
    #9860780
    +1
    любая система которая выдаст профит фактор просто больше единицы (т.е. гарантированно прибыльна) на предсказуемом конечном интервале времени — будет гениальная система.
    
    JamaGava
    14.10.2016 18:22
    #9860800
    При торговле случайным образом есть не нулевая вероятность получения профит-фактора выше 1.
    
    mezastel
    14.10.2016 23:43
    #9861174
    +1
    Языком мат.статистики она 0 a.s. (почти наверняка).
    
    JamaGava
    14.10.2016 23:56
    #9861194
    Собственно, о том какая она, эта вероятность, и была вся статья :)
    
    А случайное получение точных значений — явление вообще практически не реализуемое...
    
    mezastel
    15.10.2016 00:06
    #9861208
    +1
    Возьмите простое геометрическое броуновское движение $\textstyle \frac{dS}{S}=\mu dt + \sigma dW$ и просимулируйте произвольное кол-во входов и выходов из рынка. Посчитайте среднюю доходность. Намного более полезный результат. А если потом захотите подискутировать про неактуальность GBМ и “жирные хвосты” и все такое, тогда да, обсудим с вами и процессы Леви и Маллиавэна и что угодно.
    
    JamaGava
    15.10.2016 00:24
    #9861216
    Мне кажется, то мы с Вами говорим о несколько разных вещах… Я не спорю, что средняя доходность будет близка к 0, а средний профит-фактор к 1. Это, можно сказать, очевидно...
    
    Но когда трейдер пытается оценить стабильность своей системы, у него нет среднего профит-фактора. Есть одно значение, для которого надо дать оценку достоверности.
    
    Геометрическое броуновское — отличная модель, у меня в планах использовать его для развития предложенного в статье теста, как и для построения тестов других характеристик торговых систем (помимо профит-фактора), в первую очередь, для моего любимого коэффициента Кестнера… Но там с аналитическими выражениями пока туго :)
    
    mezastel
    15.10.2016 00:36
    #9861244
    +1
    Вообще, если интересно, я бы советовал для начала поизучать лит-ру по quant finance чтобы понять какими мы методиками уже оперируем. GBM и построенный на нем Black-Scholes это уже не модно, в ход идет намного более зубодробительная математика.
    
    JamaGava
    15.10.2016 00:44
    #9861254
    Спасибо за рекомендацию, обязательно изучу.

porfirion
14.10.2016 23:16
#9861140
+2
У меня вопрос к автору и модераторам — почему в данном случае выбран хаб «разработка»? То, что нужная модель просимулирована на python ещё не означает, что вся статья про разработку. А то так можно написать статью про использование photoshop, а в конце приписать, что был написан скрипт в 2 строки для автоматического сохранения промежуточных состояний каждый 10 минут и статья будет про «разработку»?

И теперь вопрос по сути статьи: Правильно ли я понимаю, что вся методика анализа эффективности стратегии строится на предположении, что курс на рынке — величина случайна?
Из этого следует, что методика предназначена для определения эффективности стратегии, применённой к случайному процессу.В реальности же процесс случайным не является, а следовательно эффективность «случайного» трейдера на таком процессе не подчиняется вышеуказанным формулам. А значит и сравнивать с ними не совсем корректно. По-моему это как раз и получается сравнение реальной системы на реальном рынке со «сферическим» трейдером на «сферическом» рынке.
1. JamaGava
  14.10.2016 23:21
  #9861148
  Про хаб, наверное Вы правы...
  
  Про рынок:
  предлагаемый тест аналогичен другим параметрическим стат. тестам, (таким, например, как t-тест или f-тест). Мы выдвигаем гипотезу о случайности рынка и ТС с такими-то параметрами. Строи распределение профит-фактора (модель). Сравниваем наш профит-фактор с модельным. При превышении определённого уровня (малой вероятности, что реальный профит-фактор принадлежит модельному распределению) отвергаем гипотезу о случайности. Значение, с которым сравниваем профит-фактор, определяется требуемым уровнем значимости.
  1. JamaGava
    15.10.2016 01:21
    #9861274
    А разве у меня в статье стоит хаб разработка? После Вашего комментария проверил… нет там такого хаба…
    Вот был бы отдельный хаб "разработка для биржи" или что-нибудь в этом роде…
    А то статьи по рынкам на Хабре разбросаны по совершенно разным хабам.

Gelium
14.10.2016 23:21
#9861150
+1
Каким должен быть профит-фактор, чтобы можно было говорить о стабильности данной системы? Очевидно, что чем профит-фактор выше, тем больше поводов доверять системе. А вот нижняя граница оценивается разными специалистами по разному. Наиболее популярные варианты: > 2 (так себе), > 5 (хорошая система), > 10 (отличная система). Ещё встречается такая вариация: PF_m={P-p_m \over L}, где — максимальное значение дохода по сделке, такая величина называется достоверным профит-фактором. Считается, что минимальное допустимое значение для достоверного профит-фактора 1,6.

Стратегия с PF 1.2 может быть прибыльнее стратегии с PF 5. Поэтому делать оценку возможной доходности исходя из PF отдельной сделки, по меньшей мере, не научно.

Теперь рассмотрим идеальную среду обитания «сферического трейдера» — «вакуум», то есть полностью случайный рынок.

Все бы хорошо, но рынок — это и не «вакуум», и не «атмосфера». Рынок — это «вакуум с какой-то хренью». Где в качестве «хрени» выступают абсолютно неслучайные события, перемежающиеся со случайными. Поэтому условная среда для опытов изначально не соответствует реальной.

Возможно вы великолепный математик, но как трейдеру вам еще учиться и учиться.
1. JamaGava
  14.10.2016 23:35
  #9861168
  Спасибо за комментарий.
  
  На мой взгляд, прибыльность и профит-фактор — это разные показатели для стратегии. Профит-фактор характеризует скорее надёжность, а прибыльность — это скорее следствие из профит-фактора и используемых объёмов сделок.
  Есть ещё много разных показателей…
  Мне больше нравится такой показатель, как коэффициент Кестнера. Но для него я пока не готов построить статистический тест. Хотя это и стоит у меня в планах.
  
  По поводу модели рынка… Я согласен, что рынок гораздо многообразнее "вакуума". И торговая стратегия гораздо сложнее случайных сделок.
  На рынке много чего, что мы пытаемся использовать для получения дохода, стратегия основана на обдуманных решениях… Поэтому и результат должен получиться лучше (по крайней мере не хуже) чем в "идеальном случайно-сферическом случае". Идеальная модель, по предлагаемой методике, строится как раз для оценки статистической значимости достигнутых результатов.
  
  Идея в проверке профит-фактора не по принципу "больше стольки-то", а по принципу "случайное получение таких высоких результатов маловероятно (вероятность меньше стольки-то)".

Gelium
15.10.2016 00:25
#9861220
На мой взгляд, прибыльность и профит-фактор — это разные показатели для стратегии. Профит-фактор характеризует скорее надёжность, а прибыльность — это скорее следствие из профит-фактора и используемых объёмов сделок.

В корне ошибочное мнение. PF не имеет никакого отношения к надежности стратегии вообще. От слова совсем. Надежность стратегии — это итоговая доходность. PF — только переменная в уравнении. Вы вырываете из «уравнения успеха переменную» ставите опыты с одной переменной на данных, которые не имеют никакого отношения к реальным рынкам. И что будет далее? Вы напишите, что ваши виртуальные опыты не имеют никакого отношения к реальным рынкам и вся эта статья, просто расчеты ни о чем? Или же вы попробуете как-то соотнести полученные результаты с реальными рынками и стратегиями?
1. JamaGava
  15.10.2016 00:41
  #9861250
  Я не стану в уже не знаю какой раз писать комментарий о том, почему использую модель, мягко, говоря не имеющую отношение к реальным рынкам…
  
  Я отвечу Вам примером аналогии из медицины.
  
  Есть такое понятие как плацебо — эффект полного или частичного исцеления больного при применении "пустышки", абсолютно не эффективного препарата, не имеющего никакого отношения ни к биохимии, ни к фармакологии. Грубо говоря, кусочка желатина. Но если пациент верит, что это лекарство — ему может стать лучше.
  
  Учитывая этот факт, как тестируются медицинские препараты? Они не проверяются по принципу "эффективен или нет?", они проверяются по принципу "эффективнее чем плацебо или нет?". Хотя плацебо и не имеет отношение к медикаментам.
  
  Я, по аналогии с лекарствами, предлагаю плацебо. Нереально упрощённую модель рынка и торговой системы. И если Ваша система имеет высокую доходность, в которой учтён не только профит-фактор а ещё другие составляющие, если рынок более сложен чем случаен и т.д… То пусть Ваша модель покажет результат лучше чем моя "идеальная сферическая". В противном случае, будете ли Вы так уверены в своей системе, доверите ли ей работу на больших объёмах?
  1. Gelium
    15.10.2016 10:39
    #9861394
    То пусть Ваша модель покажет результат лучше чем моя «идеальная сферическая». В противном случае, будете ли Вы так уверены в своей системе, доверите ли ей работу на больших объёмах?
    
    Я не занимаюсь построением моделей, которые не имеют отношения к практической торговле на рынке. Используемые мной, да и не только мной, модели годами работают и приносят прибыль. Поэтому я изначально знаю «правильное решение» и вижу, что у вас изначально неправильный подход, который не приведет к получению полезного для практики результата. Вы можете либо исправить ошибки и сделать что-то полезное для себя и людей, либо итогом у вас будет «недотрейдер для торговли вакуумом в среде с какой-то хренью».
    
    JamaGava
    15.10.2016 16:24
    #9861694
    Спасибо за внимание к моей работе.
    
    Я не собираюсь Вас в чём-либо переубеждать. Но и Вы меня не убедили в моей неправоте.
    Для меня Ваша позиция звучит как: "мне не нужны статистические тесты, так как я не выдвигаю ошибочных гипотез"!
    
    Gelium
    15.10.2016 17:07
    #9861730
    Попробую объяснить понятнее. В трейдинге конечная цель — это прибыль. Если взять стратегию, то параметры ее работы можно оценивать по-разному. Например, PF, число прибыльных сделок, GrossProfit и так далее до бесконечности. Вы берете одну из оценок, причем даже не оценку стратегии, а оценку сделки, и с помощью одной из оценок пытаетесь доказать или опровергнуть возможно заработать «торгуя в вакууме с какой-то хренью». Это похоже на постановку диагноза по пульсу пациента, а не по оценке его текущего состояния. PF — это пульс, а жизнь пациента не зависит только от пульса, так же, как от PF не зависит доходность стратегии.
    
    JamaGava
    15.10.2016 17:45
    #9861782
    Отличный пример моей правоты: по пульсу мы не можем поставить диагноз (достаточное условие оценки здоровья), но можем определить, что пациент в принципе жив (необходимое условие для начала диагностики). Я как раз и предлагаю проверку необходимого условия, чтобы исследуемый объект в принципе относить к торговым системам.
    
    По поводу того, что профит-фактор — это лишь один из очень многих показателей работоспособности системы, я согласен полностью! Более того, я сам чаще всего использую коэффициент Кестнера, а не профит-фактор… Но, для профит-фактора математика получается проще чем для других показателей, хотя и это "проще" само по себе не самое простое… очень надеюсь в будущем решить аналогичную задачу для Кестнера, возможно, что с более сложной моделью рынка.
    
    А про оценку сделки вместо профит-фактора — Вы не правы. Я рассматриваю, как раз-таки сумму сделок.
    
    Gelium
    15.10.2016 18:04
    #9861802
    Отличный пример моей правоты: по пульсу мы не можем поставить диагноз (достаточное условие оценки здоровья), но можем определить, что пациент в принципе жив (необходимое условие для начала диагностики).
    
    В реальной жизни вы можете по пульсу определить жив пациент или мертв, а в трейдинге наоборот, не можете, так как в трейдинге цель — стабильная прибыль не сегодня или завтра, а в долгосрочной перспективе. Если стратегия «жива» — значит она приносит доход и отдельный параметр PF об итоговом доходе не сообщает ничего. От слова совсем.
    
    А про оценку сделки вместо профит-фактора — Вы не правы. Я рассматриваю, как раз-таки сумму сделок.
    
    К сумме сделок должна прилагаться методика управления капиталом. И если сделки у вас совершаются на базе псевдослучайных данных генератора случайных чисел, то псевдослучайность таких данных — это гарантия наличия прибыльной стратегии для таких опытов. И какова тогда в итоге цель опыта?
    
    JamaGava
    15.10.2016 19:19
    #9861850
    По поводу ПФ и других параметров, я Вам уже отвечал, что для ПФ проще построить аналитическую модель. О доходе ПФ не сообщает, по крайней мере, если нет информации об объёмах. Однако, он даёт нам некоторое представление о соотношении дохода и рисков, хотя коэффициент Кестнера делает это на порядок лучше.
    
    К сумме сделок должна прилагаться стратегия мани-менеджмента — согласен на 200%! И если эта стратегия будет эффективна — то реальный профит-фактор окажется выше "сферического" с высоким уровнем достоверности. В чём собственно противоречие?
    
    Создаётся впечатление, что Вы либо не прочитали статью, либо не совсем поняли о чём там речь.
    
    Возможно, нам стоит приостановить дискуссию, до моих следующих работ, в которых я покажу практическое применение своего теста для построения торговых систем.
    
    P.S. А Вы действительно уверены в возможности построения торговой системы, которая сможет стартовав однажды, приносить доход "не сегодня или завтра"? Или всё-таки она должна будет модифицироваться, с учётом изменяющегося рынка, и для неё понадобится тест достоверности текущих показателей (в том числе надёжности)?
    
    Gelium
    15.10.2016 20:38
    #9861908
    Однако, он даёт нам некоторое представление о соотношении дохода и рисков, хотя коэффициент Кестнера делает это на порядок лучше.
    
    Я вам и пытаюсь объяснить, что вы ошибаетесь. Не дает PF никакой информации об уровне дохода и уровне риска. У одной стратегии с PF 1.2 будет доход, у другой с PF 5 будут убытки, у третьей с PF 1.3 будут убытки. И какую информацию об уровне дохода или уровне рисков вы можете получить на основании этих данных? Вы выкидываете процент прибыльных сделок, управление капиталом и далее пробуете определить опасность пребывания человека в космосе путем отправки на орбиту оторванной в аварии руки мертвого человека. Если с рукой будет все хорошо, можно отправить человека. Если рука заболеет или подпортится слишком сильно, значит и человек в космосе не выживет. Вот примерно это вы проделываете с PF относительно трейдинга.
    
    А Вы действительно уверены в возможности построения торговой системы, которая сможет стартовав однажды, приносить доход «не сегодня или завтра»? Или всё-таки она должна будет модифицироваться, с учётом изменяющегося рынка, и для неё понадобится тест достоверности текущих показателей (в том числе надёжности)?
    
    В реальном трейдинге доход считается по итогам торгового года. Надо менять стратегию или нет, тоже можно оценить по итогам года. А сферический трейдер в вакууме с хренью может торговать с виртуальной прибылью на виртуальных данных бесконечно долго. Было бы только желание подогнать эксперимент под нужный результат.
    
    JamaGava
    15.10.2016 21:38
    #9861970
    Приведите мне, пожалуйста, пример стратегии с убытками и ПФ > 1… Просто очень интересно посмотреть на такой парадоксальный феномен.
    На сколько я понимаю, если ПФ > 1, то суммарный доход больше суммарного убытка…
    
    По поводу итогов года не соглашусь. И вот почему: если Вы работаете интрадэей и за квартал у Вас накопилось порядка 300 сделок и доходность/ПФ/Кестнер/фактор_восстановления за уже не те, что за прошлый квартал, то я бы не стал ждать года. А если Вы мультимиллионер и таймфрейм ниже недели или месяца для Вас слишком мелок, то и итоги года будут ни о чём.
    Этими утрированными примерами я хотел сказать, что период пересмотра стратегии сильно завязан на инвестиционные горизонты стратегии и на репрезентативность исследуемого периода, но никак не на астрономический календарь (если речь не идёт о пересмотре финансовой стратегии компании по итогам финансового года, но это, ИМХО, из другой области).
    
    А примером с оторванной рукой Вы опять подтвердили, что наверно толкуете мою идею, изложенную в статье. Я не говорю, что если с куском мяса на орбите ничего не случилось, то в космос можно смело отправлять живого человека. Я утверждаю обратное: если условия космоса разрушат неживой объект, моделирующий человека, значит и человеку туда отправляться не стоит. А если не разрушат — это ещё ничего не значит. Ибо модель обеспечивает НЕОБХОДИМОЕ условие, а не ДОСТАТОЧНОЕ.
    
    Gelium
    15.10.2016 22:09
    #9862004
    Приведите мне, пожалуйста, пример стратегии с убытками и ПФ > 1… Просто очень интересно посмотреть на такой парадоксальный феномен.
    На сколько я понимаю, если ПФ > 1, то суммарный доход больше суммарного убытка.
    
    Да, я вас не правильно понял. Вы берете PF не сделки, а итогов стратегии. Какой смысл брать PF стратегии, имея итоговую доходность, для меня за рамками понимания и здравого смысла. Ведь PF=5 с 20% годовых хуже PF=1.2 с 200% годовых. Сразу уточняю, такое может быть за счет % выигрышных сделок и методики управления капиталом. Думаю придумать серию сделок вы самостоятельно сможете.
    
    По поводу итогов года не соглашусь. И вот почему: если Вы работаете интрадэей и за квартал у Вас накопилось порядка 300 сделок и доходность/ПФ/Кестнер/фактор_восстановления за уже не те, что за прошлый квартал, то я бы не стал ждать года.
    
    На рынке есть циклы и минимальный цикл — календарный год. Это не из области сферического вакуума, а из области практического трейдинга.
    
    Я утверждаю обратное: если условия космоса разрушат неживой объект, моделирующий человека, значит и человеку туда отправляться не стоит. А если не разрушат — это ещё ничего не значит. Ибо модель обеспечивает НЕОБХОДИМОЕ условие, а не ДОСТАТОЧНОЕ.
    
    Ну сами подумайте, если разрушение комплекса неживых объектов в космосе произошло один раз, то всё, людям в космосе не место? Ну и сколько кораблей взорвалось до полета человека в космос? А если ваша модель показала, что на рынке заработать в теории можно, то это ничего не значит, так как «модель обеспечивает НЕОБХОДИМОЕ условие, а не ДОСТАТОЧНОЕ». И какова тогда практическая польза вашего моделирования?
    
    JamaGava
    15.10.2016 22:14
    #9862008
    Люди в космос полетят в корабле или в скафандре, зная о пагубных влияниях космоса (проверив, предварительно скафандры). А методика позволит отсеять ЗАВЕДОМО СФЕРИЧЕСКИЕ СТРАТЕГИИ, случайно показавшие хорошие результаты на истории.
    
    Gelium
    15.10.2016 22:41
    #9862020
    Ваша цель понятна, но путь ее достижения для практика видится весьма странным…
    
    Допустим вы отсеяли стратегии, которые якобы показали случайно хороший результат. Далее вы берет лучшую из оставшихся стратегий и она через год сливает депозит. Ну рынок так изменился, не повезло. Берете одну из отсеянных стратегий, а она показывает доходность в 10 раз лучше, чем на истории. Ну рынок так изменился, «подогнался» под стратегию и ее параметры. И что дальше? Будете переделывать свою методику до тех пор, пока не надоест это занятие?
    
    На каждом рынке и активе есть работающие модели, которые работают за счет неслучайных событий. Какое отношение имеет моделирование на псевдослучайных данных к моделям, которые работают на реальных данных, которые включают в себя неслучайные события? А вам в голову не приходило, что моделирование на псевдослучайных данных позволяет при желании доказать как возможность создания прибыльных стратегий, так и невозможность их создания в зависимости от условий моделирования и объема данных?
    
    JamaGava
    15.10.2016 23:53
    #9862074
    Если действительно можно доказать что-то одно, то противоположное ему уже доказано автоматически с приставкой "не"… В противном случае это не доказательство, а предпосылки к выдвижению гипотезы.
    
    Как обходиться с гипотезами, каждый решает для себя сам, это может быть "религиозный" подход с твёрдой верой, статистический с уровнями значимости либо какой-то ещё.
    Вы говорите: "на каждом рынке и активе есть работающие модели, которые работают за счет неслучайных событий". Отлично. А что насчёт будущего времени? Вы ВЕРИТЕ, что эти модели будут и дальше работать? Либо исходите из ПРЕДПОЛОЖЕНИЯ, что они будут работать? Если это вопрос веры, то я не хочу участвовать в "холиваре". Если предположение, то Вам как-то надо мириться с допущением его ошибочности. Для таких случаев и используется статистика.
    
    Я предложил модель статистического подхода к принятию решения о первичном отборе торговых стратегий. Как и любой стат. тест, мой не застрахован от ошибок первого и второго рода (которые описаны в Вашем последнем примере).
    
    Результаты применения этого теста я надеюсь опубликовать в будущем. Но они будут продемонстрированы в том же "пространстве" что и Ваши "работающие модели" на ИСТОРИИ, так как будущее ни мне ни Вам не дано ни коим образом, если только Вы не пророк (лично я нет :) ).
    
    Я рад Вашей фразе "мне понятен Ваш подход".
    Но дальнейшая дискуссия рискует перейти в область священной войны концепций… Не хотелось бы. Я синкретист :)
    
    Gelium
    16.10.2016 01:27
    #9862134
    Если действительно можно доказать что-то одно, то противоположное ему уже доказано автоматически с приставкой «не»… В противном случае это не доказательство, а предпосылки к выдвижению гипотезы.
    
    В истории человечества бывали забавные истории, когда наука доказывала одно и все в это верили. Через некоторое время это опровергали и доказывали что-то другое. И все уже в это верили. Трейдинг такая же сфера, где можно доказать одно, потом доказать другое. Ну а поскольку результат лежит в информационной плоскости и не имеет никакого отношения к законам физики или математики, то взаимоисключающие доказательства могут появляться с необыкновенной легкостью.
    
    А что насчёт будущего времени? Вы ВЕРИТЕ, что эти модели будут и дальше работать? Либо исходите из ПРЕДПОЛОЖЕНИЯ, что они будут работать? Если это вопрос веры, то я не хочу участвовать в «холиваре». Если предположение, то Вам как-то надо мириться с допущением его ошибочности. Для таких случаев и используется статистика.
    
    Ни то и не другое. Ни вера, ни предположение, а практика, подтверждающая работу конкретных моделей в виде получаемого дохода. Пока условия для работы моделей сохраняются, они будут работать. Бывали времена, когда условия менялись и эти методики не работали годами. Затем снова менялись условия и они снова начинали работать. Поскольку не я один использую эти методики и доход получают другие трейдеры, это не случайное везение, которое длится годами. Плюс есть запрограммированные стратегии, которые позволяют перемещаться по шкале времени и видеть, что было бы при том или ином раскладе.
    
    JamaGava
    16.10.2016 02:15
    #9862152
    Практика вещь неоспоримая, конечно.
    
    Но есть одна проблема:
    "Проблема не в том, что человек смертен, а том, что он внезапно смертен" Мастер и Маргарита, М.Булгаков.
    
    Стратегия может перестать работать внезапно, не дожидаясь конца года. В лучшем случае, Вас частично спасут грамотные стоплоссы…
    
    В худшем:
    
    Я рекомендую Вам прочитать книгу Nassim Nicholas Taleb "The Black Swan: the impact of the highly improbable" (есть на русском). Там поднимаются очень интересные вопросы, касаемые человеческого мышления.
    
    Gelium
    16.10.2016 11:29
    #9862302
    Стратегия может перестать работать внезапно, не дожидаясь конца года. В лучшем случае, Вас частично спасут грамотные стоплоссы…
    
    Стратегии никогда не перестают работать внезапно. Динамика рынка либо меняется постепенно, и видя серию лоссов, стратегию можно изъять из портфеля, либо рынок «внезапно сходит с ума» и после одного лосса торговля останавливается до выяснения причин происходящего на рынке. Внезапные сливы происходят только у сеточников, любителей Мартингейла и торговцев без стопов. На чарты с прошлого века смотрю, так что кое что в динамике цен и фундаменте понимаю.
    
    Я рекомендую Вам прочитать книгу Nassim Nicholas Taleb «The Black Swan: the impact of the highly improbable» (есть на русском). Там поднимаются очень интересные вопросы, касаемые человеческого мышления.
    
    Благодарю, но давно уже читал эту книгу.
    
    JamaGava
    16.10.2016 12:23
    #9862368
    Мы с Вами уже начали говорить об одном и том же, только разными словами :)
    
    Gelium
    16.10.2016 12:32
    #9862382
    Поразмышляйте на досуге почему PF нельзя использовать в качестве целевого критерия оптимизации стратегии.
    
    JamaGava
    16.10.2016 13:34
    #9862424
    Обязательно поразмышляю

Alexey_mosc
15.10.2016 11:57
#9861464
Коллега, это очень интересная статья. Мне понравился аналитический подход и мысль в верном направлении. Действительно, можно смоделировать распределение ФВ для случайной торговли и сравнить правый его хвост с реальным значением на реале (обязательно на реальном форвард-тесте).

Но, я вас немного остужу.
Предположим, что рынок описывается нормальным распределением изменения значений котировок за период времени

Приращения цен на рынке не нормальны. https://www.mql5.com/ru/forum/72329/page4

Плотность распределения больше похожа на лапласовскую. Хвосты толстые. Поэтому выкладки неприменимы к рынку. Я думаю, вы сможете в Питоне взять реальные приращения и проверить их на нормальность неск.стат.тестами нулевой гипозы. И подобрать через макс.правдоподобие параметры распределения Лапласса так, что будет очень похоже. В общем, сами проверите. А теперь про идею. Вместо аналитического вывода в условиях отсутствия точного знания о виде распределения, можно делать симуляцию Монте-Карло, где по сути будет отбираться случайным образом приращения цены (в случае случайного сферического трейдера) на заданном горизонте и в нужном числе. Эти параметры можно взять из сравниваемой торговли. И смоделировать верхний квантиль распределения. Успехов!
1. JamaGava
  15.10.2016 16:22
  #9861690
  Спасибо за комментарий,
  
  Про "ненормальность" приращений я с Вами согласен, по использование хотя бы той же геометрической броуновской модели повышает сложность аналитических выкладок до пока непреодолимого для меня уровня… Но, надеюсь, всё впереди.
  
  Что касается Монте-Карло: да, это выход из положения, возможно, что единственный во многих ситуациях. Но это решение для себя и коллег-разработчиков.
  
  А хотелось бы иметь аналитический результат, который подойдёт и теоретикам :)
  1. Alexey_mosc
    17.10.2016 16:07
    #9863976
    Как мы уже обсуждали, применение выводов из предположения о нормальности ведет полученные цифры неверным путем. Наверное, иногда разница с действительными значениями может быть громадной.
    
    Возьмем чисто для примера биномиальное распределение. Статистика его будет стремится к нормальности не всегда при увеличении числа опытов. Зачастую p (q) сильно далеко от 0.5. И тогда нормальности не наблюдается, а значит нельзя считать основанную на предположении статистику (t-test, например, z-test).
    
    Именно поэтому встает вопрос применимости метода.
    
    JamaGava
    17.10.2016 20:01
    #9864384
    На самом деле, будет стремиться всё равно.
    Вопрос в количестве опытов.
    
    А что касается рынков, то вероятность изменения вверх или вниз ну никак не "p (q) сильно далеко от 0.5"…
    "Проблема" скорее в обратном :)
    
    Более того, нормальное распределении обладает максимальной энтропией из всех непрерывных распределений с теми же матожиданием и дисперсией. Это самый информационно неопределённы случай. Самая "жёсткая" модель :)
    
    Alexey_mosc
    17.10.2016 20:53
    #9864444
    Если рассматриваете распределение вероятности для направления движения (вверх / вниз), то да, биномиальное распределение будет близко к нормальному.
    
    Я же говорю про распределение price returns. Оно ненормально и причем совсем не нормально. Поэтому — несмотря на то, что нормальное распределение обладает самой высокой энтропией для непрерывной величины — вы будете сталкиваться с ситуациями, когда предсказанная вероятность вылета значения величины за пределы 2(3 и т.д.) сигм будет в реальности заниженной оценкой; вылеты будут гораздо чаще в силу длинных хвостов распределения.
    
    На этот барьер натываются многие «эконометрически заточенные» хэдж фонды и их аналитики. Оценивают волатильность через нормальное распределение, а на практике она вылетает далеко за предсказания и чаще, чем надо, — потому что на рынке акторы действуют не случайно (как молекулы) и могут формировать острые тренды через поведение толпы. Даже физически рыночный процесс не может быть нормальным.
    
    Поэтому я повторяю всегда «Зачем наступать на грабли эконометрики 20 века?».
    
    JamaGava
    17.10.2016 23:49
    #9864690
    Я не спорю, что мой подход не идеален и в нём много недочётов и недоработок. Я сам могу Вам перечислить основные:
    
    1) огрубление модели рыночных движений до нормальной
    2) сведение теста надёжности до анализа профит-фактора
    3) игнорирование управления капиталом, хотя бы в виде простой рекапитализации
    
    И поясню почему я сделал именно так:
    1) под Гауссовой моделью я подразумеваю наихудший вариант: если стратегия работает хуже чем случайная на Гауссовом рынке, то стратегия ли это вообще?
    2) огрубление Гауссовой модели я частично компенсировал учётом показателя Хёрста;
    3) профит-фактор+Гаусс — это самое простое, для чего пока получилось построить аналитическую модель, это первый шаг;
    4) реивестиование+ GBM логарифмированием доходности автоматически сводится к уже изложенному в данной статье. Осталось только придумать название для параметра (профит-лог-фактор, например :) )
    5) наверное, лучшие результаты будут при моделировании методом Монте-Карло. Но согласитесь, что аналитическая модель и в использовании проще, и для теоретических исследований лучше подходит, поэтому в данном направлении и копаю.
    
    Против стремления любого биномиального распределения к нормальному с ростом N Вы уже не возражаете? Я сам усомнился после Вашего комментария (подумал, что один хвост обрывается), проверил… Точно сходится.
    
    Alexey_mosc
    18.10.2016 12:15
    #9865326
    Против стремления любого биномиального распределения к нормальному с ростом N Вы уже не возражаете?
    
    Вы как-то слишком поспешно делаете выводы… Я сказал, что если p близко к 0.5, то сходится — это справедливо для направлений приращений цен (примерно 0.5, что пойдет в одну сторону).
    
    В общем говоря, я не только сомневаюсь. Я это знаю доподлинно. Для крайних значений p точно не сойдется (хвост будет выпирать). Все что я пишу я сам проверял и делал это in a hard way. А вот то, что вы это не знаете, это плохо.
    
    под Гауссовой моделью я подразумеваю наихудший вариант: если стратегия работает хуже чем случайная на Гауссовом рынке, то стратегия ли это вообще?
    
    С этим пожалуй я соглашусь. Консервативная оценка. Но видите-ли, вам всегда придется держать в уме информацию о том, что модель не налазит на процесс и ее грубо так сказать натянули. А я лично люблю, когда сделанная работа надежна и можно не переосмысливать.
    
    JamaGava
    18.10.2016 13:00
    #9865442
    Давайте не будем ставить друг-другу оценки, мы с Вами не на зачёте в универе.
    
    Я не знаю какой методикой Вы проверяли биномиальное распределение, но с утверждением:
    
    Возьмем чисто для примера биномиальное распределение. Статистика его будет стремится к нормальности не всегда при увеличении числа опытов. Зачастую p (q) сильно далеко от 0.5. И тогда нормальности не наблюдается.
    у меня нет оснований соглашаться. Случай бесконечно малой p или q я не рассматриваю, так как это уже не биномиальное распределение. А в остальных случаях — сходится.
    Если с ростом N растёт хвост, значит что-но пошло не так. Потому как у биномиального с ростом N показатель асимметрии стремится к 0.
    
    Если Ваш эксперимент проводился не на чистых биномиальных данных, а на рыночных, то там на самом деле не биномиальное распределение. Так как рынок обладает памятью, а биномиальное распределение описывает серию экспериментов без памяти. Возможно отсюда и несходимость к Гауссу.
    
    Alexey_mosc
    18.10.2016 16:15
    #9865964
    Я проводил эксперимент на независимых наблюдениях, не на рынке. Моделировалось биномиальное распределение с плавающими p и n(размер выборки) для случайно сгенерированных чисел. Требовалось оценить численно какую мощность будет иметь тест на реальных данных.
    
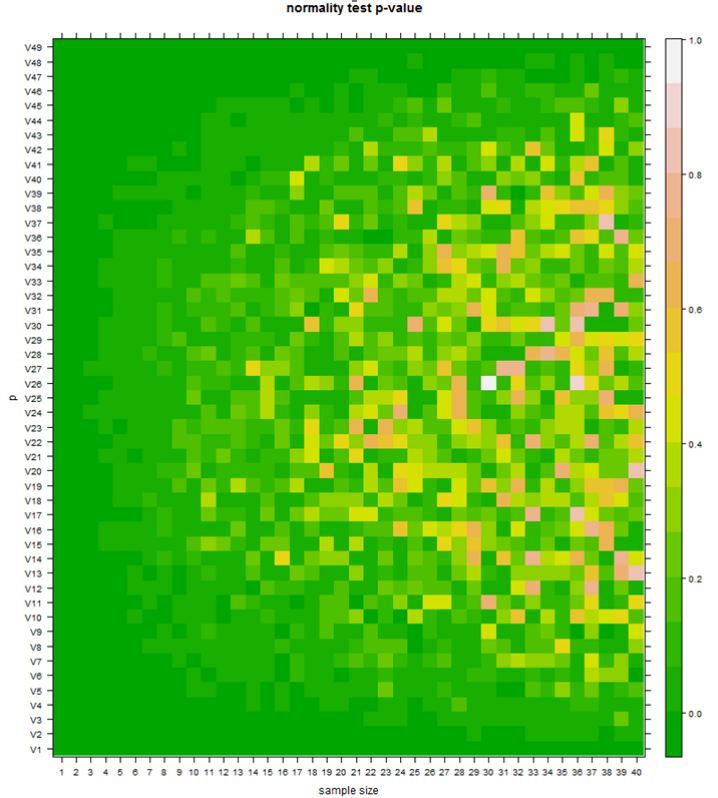    Даже для многотысячных выборок распределение отличалось от нормального при p в районе 0.01-0.03.
    
    "
    
    Здесь sample size of 50 до 2000; p от 0.02 до 0.98. Сверху и снизу области, где распределение не нормально.
    
    Это может быть важно. Если брак на производстве 0.1 процента, то значимо задетектировать изменение p (на 0.1 процента) с внедрением какого-то процесса потребует отказа от предположения о нормальности. Мои заказчики были в этом плане требовательны.
    
    Согласен, это довольно особый пример. Но такая же штука может случиться и например при подсчете частоты кликов по баннерам на число посетителей сайта. То есть, это явление встречается в жизни.
    
    Да, я просто подтруниваю. Но цель одна — улучшение качества описывающих рынок моделей.
    
    JamaGava
    18.10.2016 23:02
    #9866584
    Интересная задачка.
    
    Что касается эксперимента: правильно ли я понимаю, что жёлтое пятно в центре — это область, в которой биномиальное распределение сходится к нормальному?
    
    Если да, то обратите внимание, на то, что эта область расширяется. Если бы Вы продлили ось абсцисс влево, то увидели бы как области вверху и внизу заполняются жёлтым. Это вполне объяснимо: для p=0.02 или p=0.98 при N=2000 короткий хвост обрезан на длине примерно в 6 сигма. В то время как для p=0.5 уже при N=500 хвосты длиной в 22 сигма (почувствуйте разницу).
    
    Чтобы получить такой же длины короткий хвост (измеренный в сигмах) для p=0.02 нужно N=24000.
    
    Другое дело, если на практике нереально получить такой объём данных, то можно говорить, что в данных условиях, мы не можем полагаться на "огауссианивание" данных.
    
    Но и говорить, что биномиальное плохо себя ведёт — неправомерно.
    
    Alexey_mosc
    19.10.2016 15:09
    #9867654
    Да, согласен со всем сказанным. Для выборки стремящейся к бесконечности биномиальное все равно будет довольно точно сходится к нормальности.
    
    Если ограничена выборка — в нашем случае стоимость каждого наблюдения была значительной и объяснить менеджементу почему 300 будет лучше чем 150 надо было очень сОлидно — возникают проблемы.
    
    из вики:
    рекомендуется применять при n > 100 и npq > 20.
    
    если у нас 1000 наблюдений (выборка по-любому будет ограничена сверху), p=0.02, то npq = 19.6, что уже на грани. Ну, вы поняли.
    
    Тут уже более тонкий вопрос конвенций, которые используются группой специалистов. Если мы видим потенциальный источник отклонения выборочных средних от нормального распределения, мы делаем неск.тестов, в том числе непараметрических.
    
    Если мы говорим про непрерывную случ.величину, и мы наблюдаем, что она ненормальна, то не стоит также ожидать, что на конечных выборках распределение статистики станет нормальным. Точно также, практика наложит жесткие ограничения на применимость параметрических методов.
    
    Еще один вопрос, который может быть интересным.
    
    Выборки часто сильно ограничены. Например, у вас сделки длятся 6 часов. Для тестирования на отложенной выборке заложено 3 года. Максимум будет 3168 сделок. Допустим, Вы наблюдаете, что доля прибыльных сделок на реальной торговле 0.52, а в среднем при моделировании случайной торговли получается 0.49 (не забываем про влияние спреда). Значимо ли отличаются частоты? Тут сходимость к нормальности будет хорошая. Но если посчитать мощность теста на разницу пропорций:
    
    library(pwr) pwr.2p.test(h = 0.03, n = 3168, sig.level = 0.01, power = NULL, alternative = "greater")
    
    получим:
    power = 0.1287409
    
    То есть, тоже не АЙС.
    
    JamaGava
    19.10.2016 19:01
    #9868238
    Полностью согласен.
    
    Для приведённого Вами примера желателен больший разбег для теоретической и практической величин.
    
    И согласен с тем, что статистика как теория не всегда применима на практике.
    
    Но и без "формульного" фундамента на практиковать тяжеловато будет. Приходится искать баланс.
    
    Alexey_mosc
    19.10.2016 19:15
    #9868270
    Для приведённого Вами примера желателен больший разбег для теоретической и практической величин.
    
    Я намекаю, что для реальных данных детекция значимых отклонений будет не простой ))

Fasakhov
15.10.2016 16:12
#9861670
Ждем второй части. Описания тестирования на торговых системах. Только бы слово «форекс» убрать. Слишком много негативных ассоциаций. Потестировать фъючерсный рынок было бы интересно. Доступ к данным что русского рынка, что США есть же.
1. Gelium
  15.10.2016 20:39
  #9861910
  А вас не смущает, что на бирже торгуются фьючерсы на валюту и биржевой «Форекс» через арбитраж связан с внебиржевым как сиамские близнецы? ;-)

JamaGava
15.10.2016 16:15
#9861680
Спасибо за комментарий.

Да, про слово "форекс" я согласен с Вами. Для многих, видимо, болезненная тема.

А что касается второй части — она в ближайшей перспективе… Только примеры будут как раз-таки с форекса :)