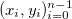 и соответствующий им набор положительных весов
и соответствующий им набор положительных весов 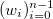 . Мы считаем, что некоторые точки могут быть важнее других (если нет, то все веса одинаковые). Неформально говоря, мы хотим, чтобы на соответствующем интервале была проведена красивая кривая таким образом, чтобы она «лучше всего» проходила через эти данные.
. Мы считаем, что некоторые точки могут быть важнее других (если нет, то все веса одинаковые). Неформально говоря, мы хотим, чтобы на соответствующем интервале была проведена красивая кривая таким образом, чтобы она «лучше всего» проходила через эти данные. 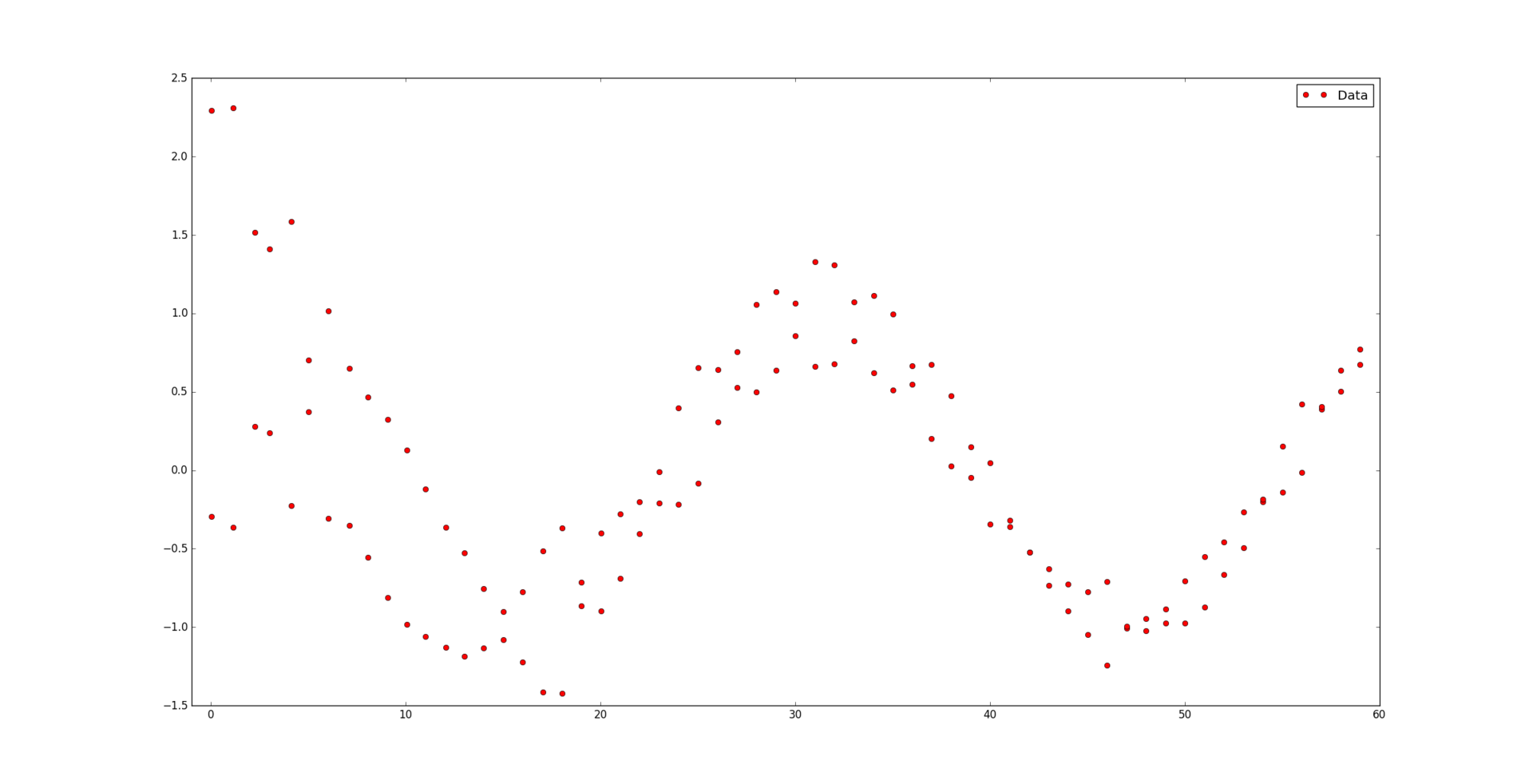
Под катом находится алгоритм, раскрывающий, каким образом сплайны позволяют строить подобную красивую регрессию:
Основные определения
Функция s(x) на интервале [a, b] называется сплайном степени k на сетке с горизонтальными узлами
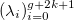 , если выполняются следующие свойства:
, если выполняются следующие свойства:- На интервалах
 функция s(x) является полиномом k-й степени.
функция s(x) является полиномом k-й степени. - n-ая производная функции s(x) непрерывна в любой точке [a, b] для любого n = 1,…, k-1.
Заметим, что для построения сплайна нужно для начала задать сетку из горизонтальных узлов. Расположим их таким образом, чтобы внутри интервала (a, b) стояло g узлов, а по краям — k+1:
 и
и 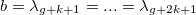 .
.Каждый сплайн в точке
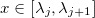 может быть представлен в базисной форме:
может быть представлен в базисной форме:
где
 — B-сплайн k+1-го порядка:
— B-сплайн k+1-го порядка:

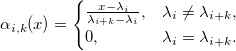
Вот как, например, выглядит базис на сетке из g = 9 узлов, равномерно распределенных на интервале [0, 1]:

Сходу разобраться в построении сплайнов через B-сплайны очень сложно. Больше информации можно найти здесь.
Аппроксимация с заданными горизонтальными узлами
Итак, мы выяснили что сплайн определяется однозначно узлами и коэффициентами. Допустим, что узлы
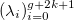 нам известны. Также на вход подается набор данных
нам известны. Также на вход подается набор данных 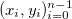 с соответствующими весами
с соответствующими весами 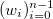 . Необходимо найти коэффициенты
. Необходимо найти коэффициенты  , максимально приближающие кривую сплайна к данным. Строго говоря, они должны доставлять минимум функции
, максимально приближающие кривую сплайна к данным. Строго говоря, они должны доставлять минимум функции
Для удобства запишем в матричном виде:

где


Заметим, что матрица E блочно-диагональная. Минимум достигается когда градиент ошибки по коэффициентам будет равен нулю:

Зададим оператор
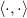 , обозначающий взвешенное скалярное произведение:
, обозначающий взвешенное скалярное произведение: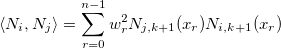
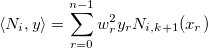
Пусть также
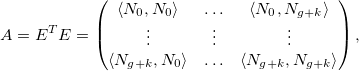

Тогда вся задача и все предыдущие формулы сводятся к решению простой системы линейных уравнений:

где матрица А (2k+1)-диагональная, так как
 , если |i — j| > k. Также матрица А симметричная и положительно-определенная, следовательно решение возможно быстро найти с помощью разложения Холецкого (существует также алгоритм для разреженных матриц).
, если |i — j| > k. Также матрица А симметричная и положительно-определенная, следовательно решение возможно быстро найти с помощью разложения Холецкого (существует также алгоритм для разреженных матриц).И вот, решая систему, получаем желаемый результат:

Сглаживание
Однако, далеко не всегда все так хорошо. При малом количестве данных по отношению к количеству узлов и степени сплайна может возникнуть проблема т.н. сверхподгонки (overfitting). Вот пример «плохого» кубического сплайна, при этом идеально проходящего сквозь данные:
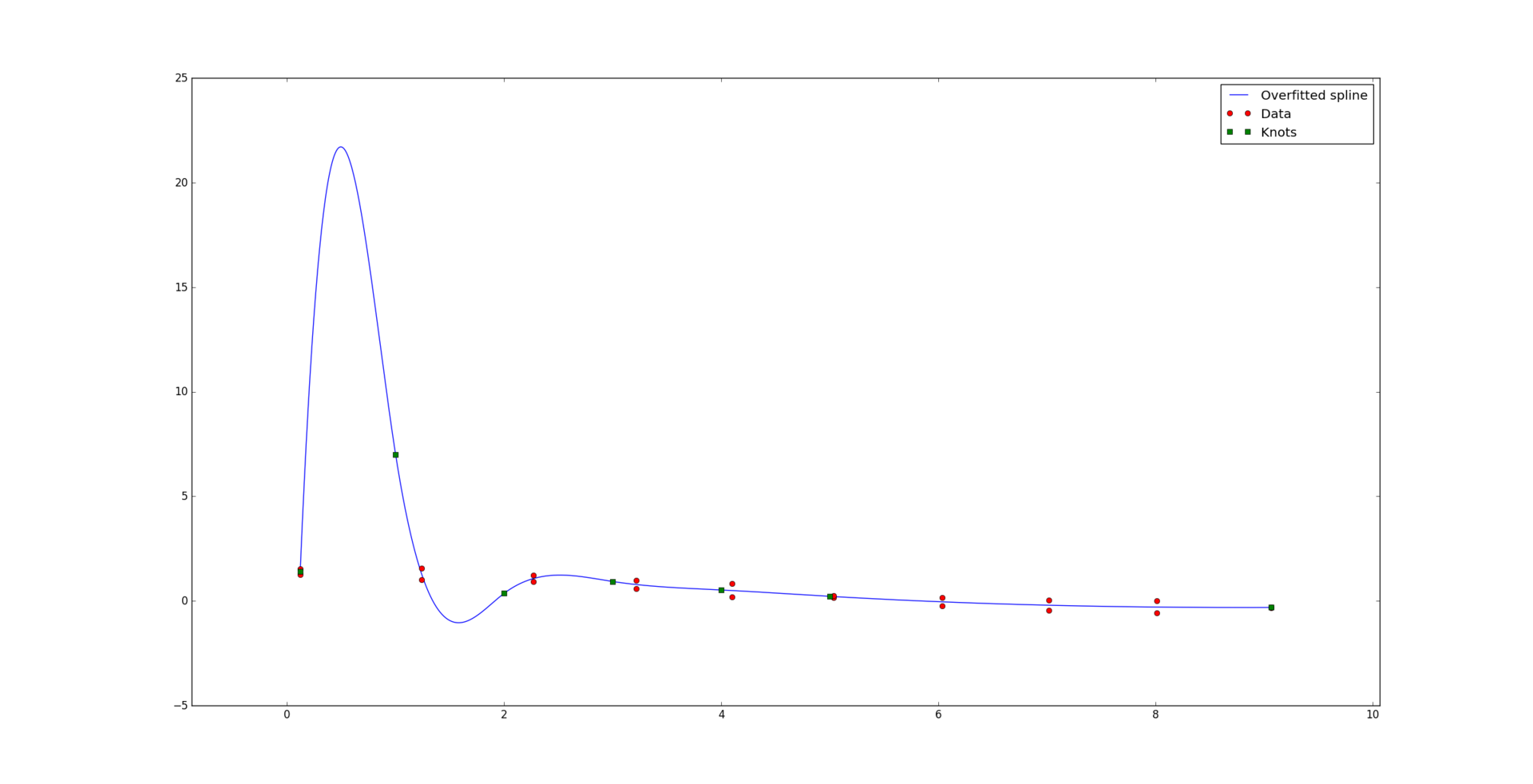
Окей, кривая уже не такая уж и красивая. Попытаемся уменьшить так называемые колебания сплайна. Для этого мы попробуем «сгладить» его k-ю производную. Другими словами, мы минимизируем разницу между производной слева и производной справа от каждого узла:
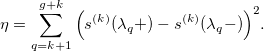
Разложив сплайн в базисную форму, мы получаем:

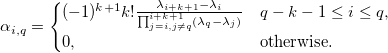
Давайте рассмотрим ошибку

Здесь q — вес функции, влияющей на сглаживание, и
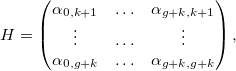
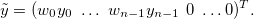
Новая система уравнений:
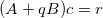
где
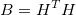
Ранг матрицы B равен g. Она симметричная и, так как q > 0, A + qB будет положительно определенной. Поэтому разложение Холецкого по-прежнему применимо к новой системе уравнений. Однако, матрица B вырожденная и при слишком больших значениях q могут возникнуть численные ошибки.
При совсем маленьком значении q = 1e-9 вид кривой изменяется очень слабо.
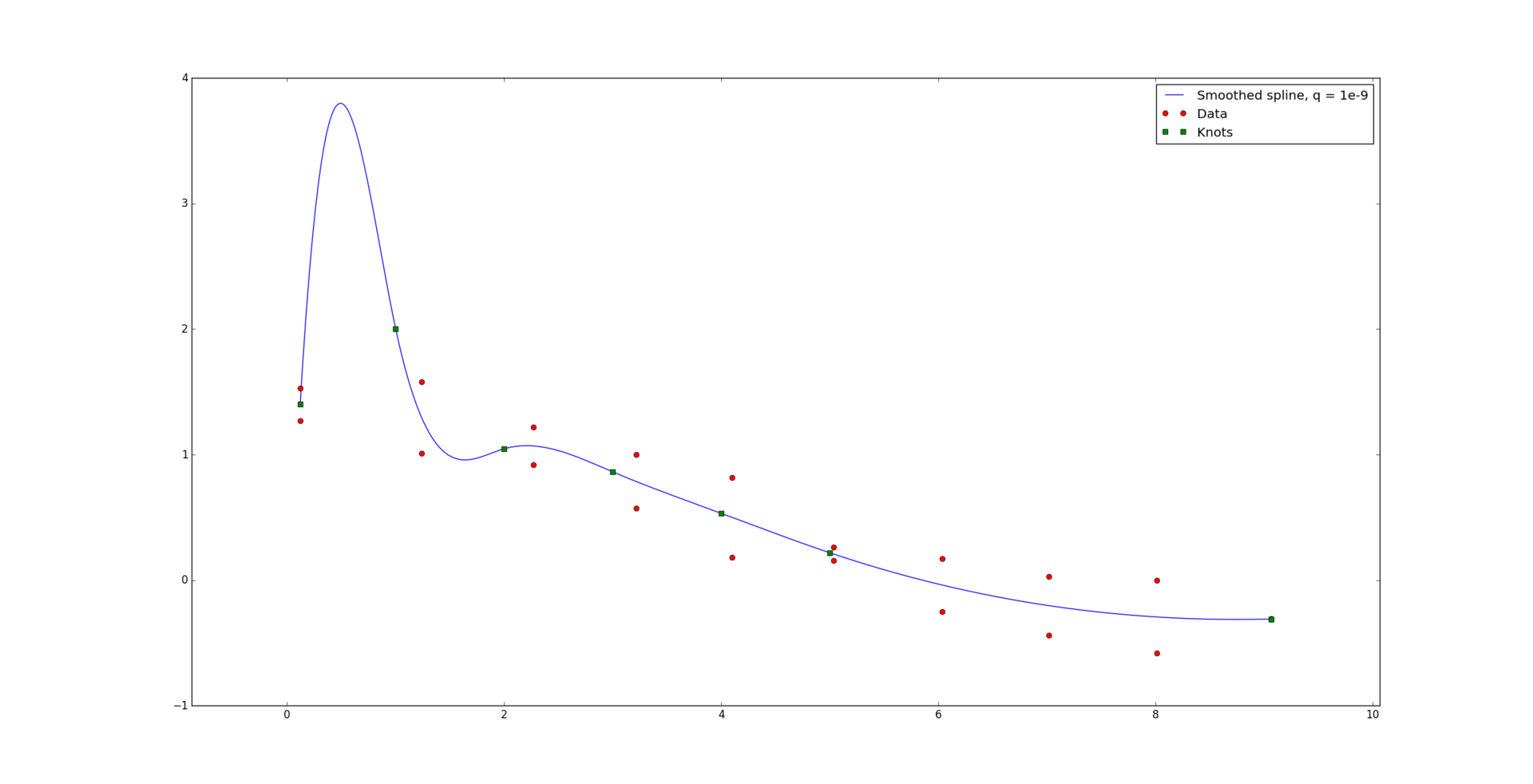
Но при q = 1e-7 в данном примере уже достигается достаточное сглаживание.

Аппроксимация с неизвестными горизонтальными узлами
Представим теперь, что задача такая же, как и прежде, за исключением того, что мы не знаем как узлы расположены на сетке. На вход кроме данных подается только количество узлов g, интервал [a, b] и степень сплайна k. Попробуем наивно предположить, что лучше всего расположить узлы равномерно на интервале:

Упс. Видимо, необходимо все-таки расположить узлы как-то иначе. Формально, расположим узлы таким образом, чтобы значение ошибки

было минимально. Последнее слагаемое играет роль штрафной функции, чтобы узлы не сильно приближались друг к другу:
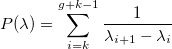
Положительный параметр p — вес штрафной функции. Чем больше его значение, тем быстрее узлы будут удаляться друг от друга и стремиться к равномерному расположению.
Для решения данной задачи мы используем метод сопряженных градиентов. Его прелесть заключается в том, что для квадратичной функции он сходится за фиксированное (в данном случае g) количество шагов.
- Инициализируем направление
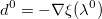 .
.
Как рассчитать производную ошибки по узлам?Производная суммы квадратов по узлу:

Для того, чтобы рассчитать влияние положения узла на значения сплайна, нужно рассмотреть B-сплайны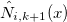 на новых узлах
на новых узлах  и с новыми коэффициентами
и с новыми коэффициентами 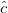



Производная штрафной функции:

На производную функции сглаживания без слез не взглянешь:

- Для j = 0,…, g-1
- Зададим функцию

возвращающую ошибку в зависимости от выбора шага вдоль заданного направления. На этом шаге мы находим оптимальное значение ?*, доставляющее минимум этой функции. Для этого мы решаем задачу одномерной оптимизации. О том, каким образом, будет сказано позже.
- Обновляем значения узлов:

- Обновляем вектор направления:

- Зададим функцию
- Если
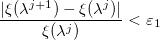
и

где ?1 и ?2 — заранее заданные величины, отвечающие за точность работы алгоритма, то выходим. Иначе, обнуляем счетчик и возвращаемся на первый шаг.
Решение задачи одномерной минимизации
Для того, чтобы найти значение
 , доставляющее минимум функции
, доставляющее минимум функции 
мы используем алгоритм, позволяющий сократить количество обращений к оракулу, а именно количество операций аппроксимации с заданными узлами и подсчета функции ошибки. Мы будем использовать нотацию
 .
.- Пусть первая и последняя компоненты вектора направления равны нулю:
 . Зададим также максимально возможный шаг вдоль этого направления:
. Зададим также максимально возможный шаг вдоль этого направления:
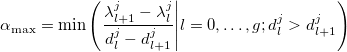
Такой выбор обусловлен тем, что узлы не должны пересекаться.
- Инициируем k = 0 и начальные шаги:
 ,
, 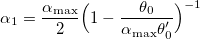 ,
,  .
. - До тех пор, пока
 :
:
- Задаём

и уменьшаем шаг

- k = k + 1
- Задаём
- Если k > 0, то возвращаем ?* = ?1. Иначе:
- До тех пор, пока
 : ?0 = ?1, ?1 = ?2 и
: ?0 = ?1, ?1 = ?2 и

- Возвращаем
 , где
, где  — корень уравнения I'(?) = 0 и I(?) — аппроксимация функции ошибки:
— корень уравнения I'(?) = 0 и I(?) — аппроксимация функции ошибки:

где
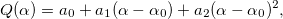

- До тех пор, пока
Коэффициенты ai и bi могут быть найдены из уравнений

и

Объяснение алгоритма:
Идея заключается в том, чтобы расставить три точки ?0 < ?1 < ?2 таким образом, чтобы по значениям ошибок, достигаемых в этих точках, можно было построить простую аппроксимирующую функцию и вернуть её минимум. Притом значение ошибки в ?1 должно быть меньше, чем значение ошибки в ?0 и ?2.
Находим начальное приближение ?1 из условия S'(?1)=0, где S(?) — функция вида
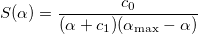
Константы c0 и c1 находятся из условий
 и
и  .
.Если мы просчитались с начальным приближением, то мы уменьшаем шаг ?1 до тех пор, пока он доставляет большее значение ошибки, чем ?0. Выбор
 исходит из условия
исходит из условия  , где Q(?) — парабола интерполирующая функцию ошибки
, где Q(?) — парабола интерполирующая функцию ошибки 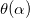 :
: 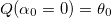 ,
,  и
и 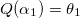 .
.Если k > 0, то мы нашли значение ?1, такое что при его выборе значение ошибки будет меньше, чем при выборе ?0 и ?2, и мы возвращаем его в качестве грубого приближения ?*.
Если же наше первоначальное приближение было верным, то мы пытаемся найти шаг ?2, такой что
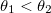 . Он будет найден между ?1 и ?max, так как ?max — точка сингулярности для штрафной функции.
. Он будет найден между ?1 и ?max, так как ?max — точка сингулярности для штрафной функции.Когда найдены все три значения ?0, ?1 и ?2, мы представляем функцию ошибки в виде суммы двух функций, приближающих разность квадратов и функцию штрафа. Функция Q(?) — парабола, чьи коэффициенты могут быть найдены, так как мы знаем её значения в трех точках. Функция R(?) уходит на бесконечность при ?, стремящемся к ?max. Коэффициенты bi также могут быть найдены из системы из трех уравнений. В результате, мы приходим к уравнению, которое может быть приведено к квадратному и легко решено:

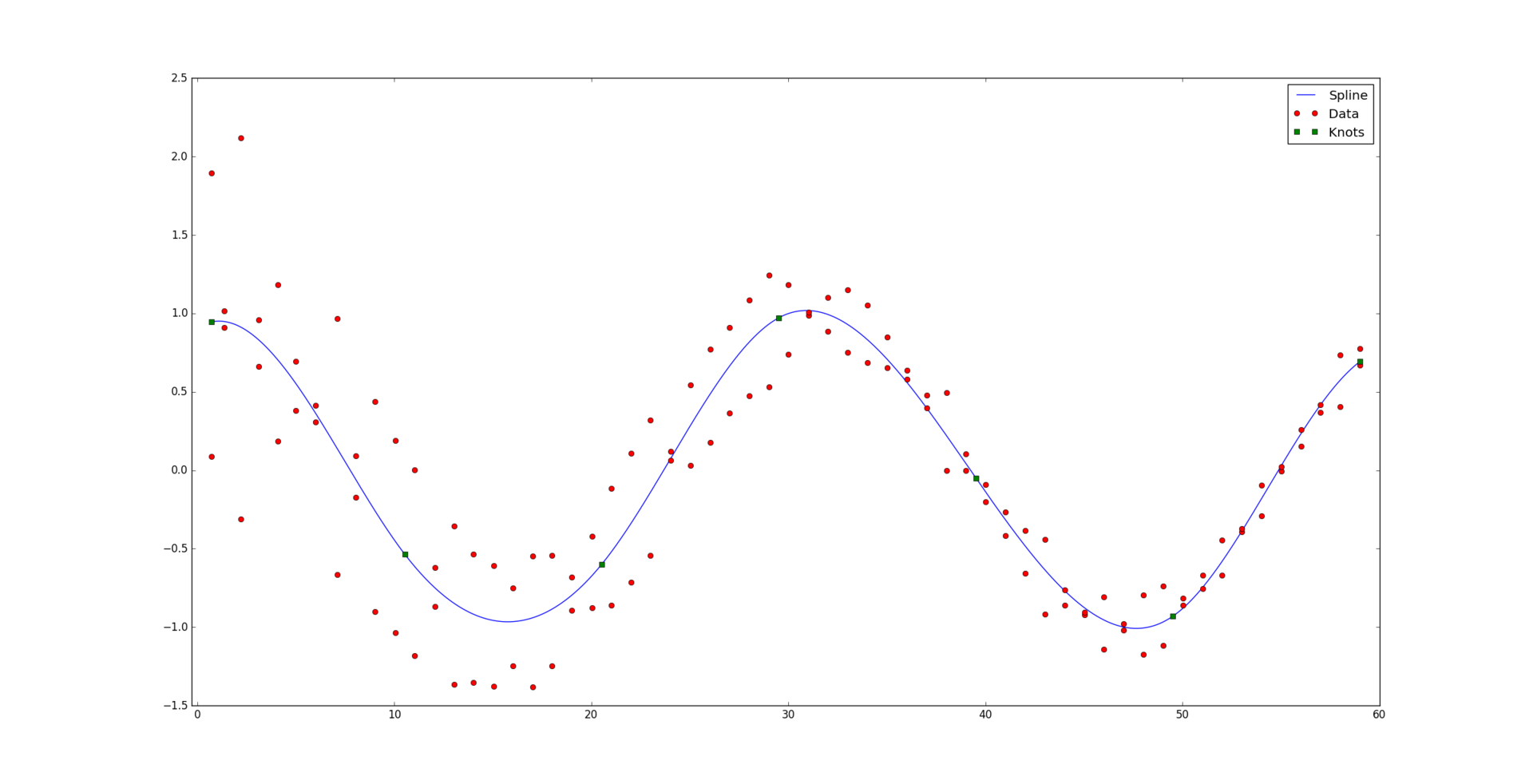
И вот, для сравнения, результат оптимально построенного сплайна:
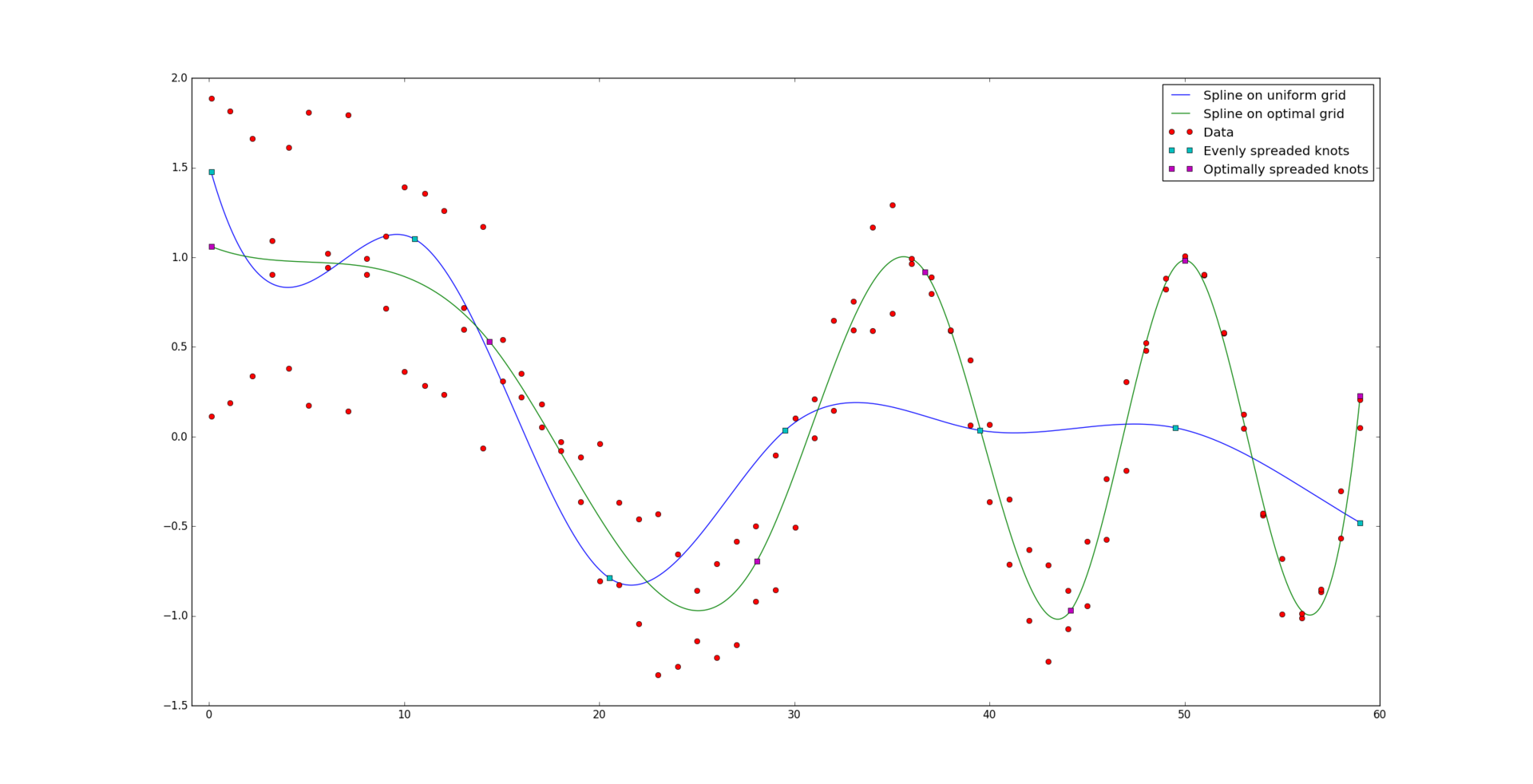
Ну и для тех, кому может пригодиться: реализация на Python.
Комментарии (15)

JIuBeHb
07.12.2016 23:23Приблизительно год назад я решал задачу аппроксимации массива точек в трехмере при помощи сплайн-плоскости. К сожалению, массивы у меня были «плохие» и постоянно получались «колодцы» или «горы» там, где их быть не должно, как в примере автора.
В сети очень много сплайн-алгоритмов и их реализаций на различных языках именно для двумерных случаев (первая половина статьи, например, повторяет методичку, которую нам раздавали на втором курсе), а вот для трёхмерных и, тем более, n-мерных случаев толковых алгоритмов, а тем более реализаций, я лично найти не смог.
Может быть автор или кто-нибудь ещё сможет описать реализацию подобных «гладких» сплайнов для трехмера?
The_Freeman
08.12.2016 17:01Посмотрите книгу Curve and Surface Fitting with Splines (Numerical Mathematics and Scientific Computation), автор Paul Dierckx. Основные идеи в статье взяты оттуда.

kanikeev
08.12.2016 01:33Человеческим зрением вижу две кривых на первом рисунке. Вы ничего в критериях не потеряли?
3aicheg
08.12.2016 04:25-7Очередной сэнсэй дорвался до редактора формул и наваял «туториал», ненужный тем, кто умеет и непонятный тем, кто не умеет :)

Refridgerator
08.12.2016 06:26В своё время пытался подобным образом решать аналогичную задачу, но не осилил, заткнулся на выборе узлов. Решил её другим способом — последовательной аппроксимацией функцией a*sin(k*x)+b*cos(k*x)
0serg
08.12.2016 08:59+2Неплохая статья, но предложенный метод решения проблемы наименьших квадратов не самый устойчивый — вычисление AT A возводит число обусловленности проблемы в квадрат. Часто надежнее (но медленнее) для подобных проблем использовать SVD

aso
08.12.2016 09:57На всякий случай скажу очевидную вещь — выбор критериев остаётся делом произвола и не имеет однозначных формальных критериев.
Ну т.е. приведённые «нехорошие примеры» — в реальности, в некоторых случаях — могут оказаться вполне хорошими.
Понимать это может только человек, подбирающий сплайн.

Caduceus
08.12.2016 10:21Я нечто подобное в свое время генетическим алгоритмом делал. Довольно забавно в динамике наблюдать, как кривая подстраивается под точки.

Refridgerator
09.12.2016 07:26+3Чтение математической литературы может быть увлекательнее любого детектива.
Сначала — завязка. Поставлена понятная задача и показано решение. Интересно, открываем.
Функция s(x) на интервале [a, b] называется сплайном степени k на сетке с горизонтальными узлами
Что за g, почему 2k? Интрига. Но уже в следующем предложении интрига раскрывается, заодно показывая несколько иллюстраций, из которых понятно, что «ну это всё просто!». Расслабляемся и читаем дальше.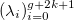
Строго говоря, они должны доставлять минимум функции
Хмм… Похоже на метод наименьших квадратов. Приятно чувствовать, что какие-то знания у меня есть. И тут вдруг — неожиданный поворот сюжета:

Для удобства запишем в матричном виде:
Что за палочки, что за цифры, нас такому не учили! Страшно. И хотя дальше матрица в привычном представлении присутствует, чувство тревоги не уходит. И вот:

Тогда вся задача и все предыдущие формулы сводятся к решению простой системы линейных уравнений:
Звучит как очевидный факт, но мне же это совсем не очевидно! Расстроившись, я пошёл пить чай.
(спустя некоторое время)
Хм… Минимизировать разницу между производными для обеспечения гладкости — это сильно!
(спустя ещё некоторое время)
Что-то формул всё больше и больше. Посмотрю-ка я пока просто картинки, а к формулам попозже вернусь.
…
(финал)
О, код на питоне! Написан вроде неплохо. Значит, теперь в формулы не обязательно вникать, можно же и отладчиком прогнать, если вдруг что. Облегчение.
(вместо заключения)
Многие авторы математических алгоритмов не прикладывают к своим статьям никакого кода, считая, что для программиста его математические выкладки должны быть очевидными. К сожалению, это редко когда так. Для программиста конструкция for(){for(){...}} более понятна, чем ? ?, даже если знать, что ? — это сумма, и несмотря на то, что она длиннее. Поэтому автору отдельный респект за код.

pchelintsev_an
09.12.2016 16:14Вот это хороший материал! Идеально подходит как для исследований, так и для лекций. А есть Интернет-ссылки на какие-нибудь работы автора в научных журналах, чтобы потом сослаться?

The_Freeman
09.12.2016 17:14Как я писал выше, Вы можете сослаться на книгу «Curve and Surface fitting with splines» автора Paul Dierckx. Я лишь модифицировал взятый оттуда алгоритм.
А лично у меня лишь одна статья в англоязычном научном журнале, и ссылаться на неё Вам вряд ли придётся =)


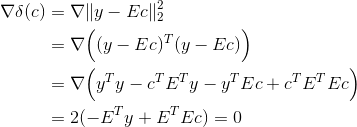
gudvinr
У вас есть возможность собрать пакет для PyPI?
hombit
Если я правильно понимаю, все уже сделано в
scipy: https://docs.scipy.org/doc/scipy/reference/generated/scipy.interpolate.UnivariateSpline.html