Ю.А. Бычков, С.В. Щербаков
Исследование качественных особенностей динамики математических моделей нелинейных неавтономных систем с помощью собственных чисел функциональной матрицы Якоби
Постановка задачи
Задача исследования качественных особенностей динамики математических моделей нелинейных неавтономных систем с сосредоточенными параметрами чрезвычайно актуальна. Развитие теории нелинейных явлений и получаемые прикладные результаты порождают многообразие методов решения этой задачи [1-3].
В общем случае динамику математических моделей систем выделенного класса (далее «систем») описывает следующее обыкновенное нелинейное интегрально-дифференциальное уравнение с нестационарными коэффициентами:
где – оператор обобщённого дифференцирования по независимой переменной ; – квадратная, порядка , матрица с полиномиальными от и элементами, где — оператор интегрирования с переменным верхним пределом ;
G(D) –прямоугольная матрица, размером , с полиномиальными от и элементами; и – матрицы-столбцы координат системы (искомых решений) и внешних воздействий на неё соответственно; – матрица-столбец со строками в виде сумм произведений, сомножители которых — нестационарные коэффициенты, а также классические производные любого порядка и интегралы любой кратности, начиная с нулевых, от искомых решений и внешних воздействий, в произвольных дробно-рациональных степенях.
Расчёт динамики нелинейных неавтономных систем при заданных предначальных условиях , , , сводится к поиску всех существующих в заданном интервале исследования решений уравнения (1) и сопряжён с рядом алгоритмических и математических проблем. Существо этих проблем определяет объективное разнообразие качественных особенностей искомых решений.
В общем случае характер динамики искомых решений уравнения (1) непредсказуем, это обусловлено зависимостью форм проявления доминирующих нелинейных и нестационарных свойств системы от выбранных начальных условий, соотношения параметров и вида её характеристик. В общем случае показатели искомых решений уравнения нерегулярны, сводя динамику системы к так называемому детерминированному хаосу [2-4]. Характеризуя её динамику, отметим, что в искомых решениях уравнения возможны разрывы первого рода, в том числе дифференцируемые, и разрывы второго рода. Специфика этих решений в том, что они, как правило, сопряжена с «жесткостью», т.е. с чередованием интервалов быстрого и медленного изменения их динамических показателей, причём в пределах таких интервалов возможны переходы от локальной устойчивости к неустойчивости и наоборот. Прямым следствием локальной неустойчивости служит эффект «перемешивания» решений, что значительно усложняет задачу численного расчёта динамики нелинейной неавтономной системы и анализа её качественных особенностей [5]. Возможное качественное разнообразие особенностей динамики нелинейной неавтономной системы, являясь следствием многосложного переплетения её координатно-параметрических взаимосвязей, допускает лишь приближённое решение уравнения с использованием того или иного численного метода [6-8]. Численных методов много и их расчётные схемы постоянно совершенствуются. Тем не менее, ни один из них не позволяет установить в замкнутой форме какие-либо взаимосвязи или закономерности между характером поведения искомого решения уравнения и информационными показателями этого уравнения. Задача выделения таких взаимосвязей и организация на их основе последующего анализа качественных особенностей и свойств решений уравнения важна как в теоретическом, так и в прикладном плане. Её решение означает очередной шаг к пониманию содержания причинно-следственных соотношений в нелинейных и нестационарных явлениях.
В статье дано решение поставленной задачи на основе использования в качестве информационных показателей динамики нелинейной неавтономной системы собственных чисел соответствующей её уравнению динамики функциональной матрицы Якоби и декомпозиции по таким собственным числам решений этого уравнения. В качестве расчётной основы использован аналитически-численный метод, который по своим вычислительным характеристикам соответствует поставленной задаче [9,10]. Приведён иллюстрирующий пример.
Выделение информационных показателей динамики нелинейной неавтономной системы
В состав информационных показателей качественных особенностей искомых решений уравнения целесообразно включить такие, которые определяют взаимодействие параметров этого уравнения и нестационарных показателей самих решений. В линейной стационарной системе, динамику которой описывает уравнение при , такими информационными показателями служат корни следующего характеристического уравнения:
где — определитель матрицы , при замене оператора на оператор .
Характер и численные значения корней уравнения , определяют все особенности и свойства динамики линейной автономной системы в переходном процессе, включая устойчивость и «жесткость» [1,7,8]. Так как внешние воздействия однозначно регламентируют характер установившегося режима, то динамика линейной автономной системы полностью предсказуема в полубесконечном интервале времени.
Направленный выбор подобных информационно ёмких и достаточно простых в определении показателей динамики нелинейных неавтономных систем пока невозможен. Насущные запросы практики, однако, требуют уже сейчас выделения доступных для вычисления и приемлемых по информационному содержанию показателей таких систем. Если пойти по тому же пути, что и для линейного случая, то логично предложение о рассмотрении в качестве необходимых информационных показателей корней уравнения , формирование которого будет связано с вычислением определителя матрицы выделенной линейной части уравнения . Трактовка смыслового содержания получаемых при этом информационных показателей неоднозначна поскольку взаимосвязь этих выделенных стационарных по сути показателей с качественными особенностями динамики нелинейной неавтономной системы не поддаётся какой-либо содержательной идентификации даже постановочно. Кроме того, когда в уравнении матрица нулевая или выделена за счёт нелинейной части этого уравнения, то корни уравнения вообще отсутствуют или их существование, а следовательно и информационное наполнение, носит условно-субъективный характер [9].
Таким образом, целевым признаком выделения приемлемых информационных показателей динамики нелинейной неавтономной системы является условие их существования и математическая взаимосвязь с числовыми показателями искомого решения уравнения . Это условие может быть выполнено, если в уравнении матрицу линейной части определённым образом выделить или дополнить за счёт матрицы нелинейной части [9,10]. Такое выделение или дополнение матрицы за счёт матрицы возможно неоднозначным образом. Все выполняемые при этом преобразования должны носить эквивалентный характер, вследствие чего динамика системы останется неизменной. В результате выделения или дополнения матрицы за счёт матрицы будет достигнута необходимая математическая взаимосвязь корней уравнения с числовыми значениями искомых решений уравнения в дискретные моменты времени, определяемые шагом численного расчёта динамики системы. Таким образом, в результате указанных преобразований уравнения корни уравнения приобретут функциональную зависимость от времени, как в отношении числовых показателей, так и качественных характеристик.
Нестационарные свойства корней уравнения , при отсутствии целевого критерия выполнения соответствующих преобразований матрицы , приводящих к появлению таких свойств, не могут сами по себе гарантировать необходимых информативных характеристик этих корней. Желаемое исследование качественных особенностей динамики нелинейных объектов диктует выбор в качестве целевого критерия формирования или преобразования уже существующей матрицы уравнения условие её совпадения с функциональной матрицей Якоби, соответствующей этому уравнению [4-8]. Алгоритм решения такой задачи изложен в работе [10]. В результате формирования или преобразования матрицы за счёт матрицы к функциональной матрице Якоби нестационарные корни уравнения приобретут статус собственных чисел матрицы Якоби.
Нестационарные собственные числа функциональной матрицы Якоби уравнения в дискретные моменты времени, определяемые шагом его численного решения, имеют определённое известное смысловое содержание [4-8]. Являясь локальной характеристикой динамики нелинейной неавтономной системы, они в бесконечно малой окрестности точки, соответствующей дискретному моменту времени t, характеризуют устойчивость и скорость изменения динамических показателей решений её уравнения динамики . В окрестности особых точек уравнения собственные числа функциональной матрицы Якоби позволяют на фазовой плоскости выделить области притяжения и отталкивания фазовых траекторий, давая таким образом прогноз в отношении предельных состояний существующих решений этого уравнения[6-8]. Соответствующие дискретным моментам времени собственные числа функциональной матрицы Якоби, характеризуя и определяя качественные особенности и свойства динамики нелинейных неавтономных систем, обусловливают актуальность задачи выявления математических признаков и информационных показателей такой взаимосвязи. Решение указанной задачи сопряжено с установлением математической взаимосвязи между выбранными нестационарными информационными показателями динамики нелинейной неавтономной системы и параметрами расчётной схемой численного метода, используемого для расчёта этой динамики. Необходимым условием для достижения указанной цели служит наличие в расчётной схеме выбранного метода соответствующей аналитической части. Вычислительный алгоритм этой аналитической части метода должен быть согласован с особенностями расчёта собственных чисел функциональной матрицы Якоби, а также обеспечивать математическую взаимосвязь между этими числами и динамическим показателями координат нелинейной неавтономной системы. Сформулированным требованиям в полной мере отвечает одношаговый аналитически-численный метод переменного порядка [9,10].
Аналитически-численный метод расчёта динамики нелинейных неавтономных систем
Побудительным мотивом к формированию аналитически-численного метода послужило желание унифицировать решение уравнения с использованием только тождественных преобразований. Отсюда вытекает описание искомых решений рядами Тейлора и последующее применение интеграла Лапласа для алгебраизации поставленной задачи.
Аналитически-численный метод расчёта динамики выделенного уравнением класса систем в заданном интервале исследования состоит из двух частей: аналитической и численной.
Аналитическая часть метода основана на аппаратах обобщённых функций, преобразования Лапласа и функционально-степенных рядов. Процедура аналитической части предваряет выполнение каждого очередного шага расчёта и сводится к следующему. Сначала, разложив функции, описывающие внешние воздействия и нестационарные параметры системы, в соответствующие им степенные ряды, а также формально описав регулярные составляющие тех искомых решений, которые входят в матрицу уравнения соответствующими им степенными рядами, правую часть этого уравнения преобразуем в матрицу-столбец, элементами строк которой теперь служат степенные ряды. Коэффициенты этих степенных рядов в общем случае неизвестны, поскольку они выражены через известные коэффициенты степенных рядов для внешних воздействий и нестационарных параметров системы, и неизвестные коэффициенты степенных рядов для регулярных составляющих некоторых из искомых решений. Выполненная операция приводит исходное уравнение к виду, необходимому для последующего применения интегрального преобразования Лапласа. Преобразовав по Лапласу переформированное уравнение и решив полученное в результате алгебраическое уравнение по правилу Крамера, для изображения искомого решения получим следующее выражение:
где
Дробно-рациональная функция, описываемая выражением (3), в общем случае, когда является неправильной и допускает её представление в виде суммы целой рациональной и правильной дробно-рациональной функций. Последующее разложение правильной дробно-рациональной функции в ряд Лорана в окрестности бесконечно удалённой точки преобразует выражение следующим образом:
Коэффициенты , , , входящие в выражение , с учётом обозначений выражения , вычисляем по следующим формулам [9,10]:
,
где
где если
где
Члены суммы в правой части последнего из равенств образуют соответственно главную и правильную части ряда Лорана для изображения искомого решенияв окрестности бесконечно удалённой точки. Оригиналом для изображения служит обобщённая функция , содержащая сингулярную и регулярную составляющие.
Итак, после выполнения аналитической части метода для искомого решенияуравнения получим следующее описание:
где — импульсные функции от нулевого до -го порядка включительно, определённые в начальной для рассматриваемого интервала расчёта точке; — весовые коэффициенты импульсных функций; — коэффициенты разложения регулярной составляющей решения в степенной ряд в правой окрестности начальной для рассматриваемого интервала расчёта точке с абсциссой [9,10].
Полученная форма описания искомого решения отражает ряд принципиальных моментов, связанных с анализом качественных особенностей динамики нелинейных неавтономных систем. Применение интегрального преобразования Лапласа позволяет в точке, соответствующей началу текущего интервала расчёта, осуществить корректный переход от известных предначальных условий к подлежащим определению начальным условиям и выделить в искомых решениях уравнения разрывы первого рода, если они существуют. Присутствие в описании сингулярной составляющей указывает на возможность выделения существующих дифференцируемых разрывов первого рода. Отметим, что сингулярная составляющая решения , если она существует, доступна для определения в дискретный момент времени, соответствующий началу текущего шага расчёта, в аналитической части метода.
Регулярная составляющая решения , как следует из описания , представлена степенным рядом и для её вычисления в текущем интервале расчёта служит численная часть метода. В основе численной части метода лежит дискретизация независимой переменной . В текущем интервале расчёта реализация численной части метода начинается с выбора соответствующей величины шага . Этот выбор регламентирован следующим равенством [9,10]:
где
Предельная величина длины текущего шага расчёта , входящая в равенство , есть результат исследования сходимости в текущем интервале расчёта числовых мажорант степенных рядов для регулярных составляющих искомых решений . Длина текущего шага расчёта , выбранная в соответствии с равенством , такова, что обеспечивает выполнение ряда значимых условий для анализа качественных особенностей динамики нелинейных неавтономных систем.
Во-первых, в текущем интервале расчёта все степенные ряды для регулярных составляющих решений сходятся к разложенным в них функциям, превращаясь в ряды Тейлора. Это указывает на существование в рассматриваемом интервале времени искомых решений , придавая всей вычислительной процедуре логический смысл и практическую целесообразность.
Во-вторых, выбранная согласно равенству величина шага расчёта обеспечивает численную устойчивость процедуры вычисления в дискретный момент времени приближённого значения регулярной составляющейискомого решения . Расчёт приближенного значения решения связан с ограничением ряда Тейлора для регулярной составляющей решения частичной суммой его первых членов. Возникающий при этом остаточный член ряда, образуя локальную погрешность расчёта, всегда ограничен и доступен для верхней оценки с помощью формул, приведённых в работах [9,10].
В третьих, длина шага всегда соответствует скорости изменения регулярных составляющих искомых решений. Такой результат обеспечивается организацией исследования сходимости степенных рядов для регулярных составляющих решений путём рассмотрения соответствующих им числовых мажорант. Их члены образованы всевозможными комбинациями коэффициентов этих степенных рядов, определяющих значения производных конечных порядков от этих составляющих решений в дискретный момент времени .
В четвёртых, отвечающая равенству величина шага расчёта такова, что позволяет организовать процедуру верхней оценки абсолютной полной погрешности расчёта приближённого значения регулярной составляющей искомого решения . Под полной погрешностью расчёта понимаем погрешность, накопленную после выполнения двух и более шагов расчёта, на каждом из которых возникает локальная погрешность расчёта.
Итак, выбрав в соответствии с равенством величину текущего шага расчёта и ограничив ряд Тейлора для регулярной составляющей решения частичной суммой его первых членов, вычисляем приближённое значение этой составляющей решения. Затем, оценив на текущем шаге локальную погрешность расчёта, вычисляем верхнюю оценку полной погрешности расчёта. Полученные таким образом численные результаты позволяют в дискретный момент времени выделить на оси ординат одномерный интервал, который содержит неизвестное точное значение регулярной составляющей искомого решения. В принятых обозначениях этот интервал в дискретный момент времени описывает следующее двойное неравенство:
Равенство и двойное неравенство описывают результаты вычислительной процедуры аналитически-численного метода на текущем шаге расчёта . Для выполнения следующего шага расчёта в заданном интервале исследования ось ординат переносим вправо на величину . После этого, выбрав из двойных неравенств , при какие-либо приближённые значения предначальных условий, повторяем описанные процедуры аналитической и численной частей метода.
### **Установление взаимосвязи информационных показателей динамики нелинейной неавтономной системы и параметров расчётной схемы аналитически-численного метода.**
Анализ выражения с учётом уравнения показывает, что достижение указанной цели возможно путем установления математической взаимосвязи между полюсами изображения искомого решения и динамическими показателями качественных особенностей и свойств регулярной составляющей этого решения. В качестве таких динамических показателей регулярной составляющей решения логично и содержательно мотивировано рассмотрение коэффициентов входящего в описание степенного ряда. Расчёт коэффициентов выполняем в аналитической части метода с помощью рекуррентных формул . Преобразование этих формул с привлечением матричного анализа приводит к их новой форме записи, которая устанавливает в явном виде необходимую математическую взаимосвязь между коэффициентами регулярной составляющей решения и полюсами изображения этой составляющей. Новые формулы для вычисления коэффициентов приведены в работе [8]. Так, например, когда все полюса изображения простые, формула для вычисления коэффициентов имеет следующий вид[8]:
Коэффициенты в этом случае вычисляем по формуле:
Коэффициенты и в формуле связаны с коэффициентами , входящими в выражение , следующими соотношениями:
Формула позволяет записать входящий в описание степенной ряд для регулярной составляющей искомого решения в этом случае в следующей новой форме[8]:
где — число, в этом случае простых, полюсов изображения .
Сформированное описание обусловливает для регулярной составляющей искомого решения следующее эквивалентное представление:
Составляющие при этом имеют следующее описание:
cистема взаимосвязанных равенств — это результат направленного преобразования входящего в равенство исходного описания регулярной составляющей решения . Согласно ей на каждом шаге расчёта возможна декомпозиция этой составляющей решения по полюсам её изображения. Декомпозиция, как и следовало ожидать, не носит абсолютного характера, поскольку через рекуррентно вычисляемые коэффициенты , входящие в формулу , для нелинейной нестационарной системы всегда сохраняется доминирующая в формировании её динамики взаимосвязь между всеми элементами представления . Декомпозиция регулярной составляющей искомого решения , описываемая системой равенств , прошла успешную апробацию при решении ряда специальных задач, связанных с формализацией процедуры исследования существования и единственности решения, выбора шага расчёта, а также при оптимизации вычислительных затрат, связанных с оценкой абсолютной локальной погрешности такого расчёта [9].
Подводя итог, сформулируем следующий алгоритм исследования качественных особенностей динамики нелинейных неавтономных систем. Сначала выполняем эквивалентное преобразование исходного уравнения динамики системы к виду, когда матрица совпадёт с функциональной матрицей Якоби, тогда полюса изображения совпадут с собственными числами этой матрицы. Последующая декомпозиция регулярной составляющей решения по этим числам обеспечит возможность организации расчётной схемы для проведения необходимых исследований. В роли нестационарных информационных показателей качественных особенностей динамики системы рассматриваем функции, описывающие изменение в заданном интервале исследования собственных чисел функциональной матрицы Якоби и элементов декомпозиции регулярной составляющей решения . Предлагаемая схема декомпозиции искомых решений уравнения по собственными числами соответствующей этому уравнению функциональной матрицей Якоби неординарна сама по себе. Это определяет новизну ожидаемых результатов, их трактовку и последующие перспективы применения. Обозначим лишь некоторые из них, поскольку полнота суждений о такой проблематике — это вопрос времени.
Знаки вещественных частей нестационарных собственных чисел функциональной матрицы Якоби в каждый дискретный момент времени обусловливают возможность выделения границ интервалов устойчивости и неустойчивости в отношении каждого из элементов декомпозиции . Такая информация первична для выявления причинно-следственных отношений между условиями устойчивости регулярной составляющей решения и подобными условиями для самих элементов этой составляющей. Условия устойчивости или неустойчивости регулярной составляющей искомого решения при этом станут следствием существования среди нестационарных собственных чисел функциональной матрицы Якоби одного или нескольких доминирующих, а также от особенностей взаимодействия этих доминирующих чисел в интервале исследования, включая вариацию их характера.
Динамические показатели элементов декомпозиции во взаимосвязи с нестационарными собственными числами функциональной матрицы Якоби определяют исходные положения для иной трактовки результата расчёта динамики нелинейной неавтономной системы, описываемого двойным неравенством . Математическая взаимосвязь и соотношение в ходе расчёта показателей двойного неравенства и двойных неравенств, подобных неравенству , но для соответствующих элементов декомпозиции , при нерегулярности динамических свойств системы, служат основанием для выделения характерных соотношений и сочетаний между элементами декомпозиции , при которых искомые решения уравнения наиболее чувствительны к изменению параметров и внешних воздействий системы. Анализ полученных при этом результатов обусловливает возможность выделения условий, определяющих возникновение бифуркации, или диапазонов начальных условий, приводящих к «перемешиванию» фазовых траекторий [5].
Качественные особенности и характерные свойства функций, описывающих изменение в заданном интервале исследования нестационарных собственных чисел функциональной матрицы Якоби, включая непрерывность и монотонность этих функций, наличие точек экстремумов, вариативность характера таких чисел и знака их вещественных частей, несомненно, отражают существо внутренних причинно-следственные связей уравнения . Вследствие этого особенности и свойства этих функций представляют в высшей степени адаптивные показатели качественных особенностей динамики нелинейной неавтономной системы. Многообразие содержательного спектра и вариативность форм проявлений таких показателей динамики системы ещё подлежат определению и это составляет самостоятельную задачу, решение которой, возможно, послужит отправной точкой для более полного понимания многосложного и неоднозначного поведения нелинейного объекта исследования. Выделение и классификация соотношений между указанными функциональными показателями и качественными особенностями нелинейной неавтономной системы должна привести к появлению новых вычислительных алгоритмов анализа нелинейных и нестационарных явлений, включая определение условий существования динамики регулярного характера или перехода к детерминированному хаосу [2-5].
Заключение
Описываемая системой равенств декомпозиция регулярных составляющих искомых решений уравнения вводит в рассмотрение и активизирует в качестве самостоятельного вычислительного инструментария анализа динамики нелинейной неавтономной системы собственные числа функциональной матрицы Якоби. Они генерируют особенности и динамические свойства элементов декомпозиции . Как показано в приведённом далее примере, анализ таких особенностей и динамических свойств элементов декомпозиции приводит к выделению новых условий существования одного из характерных свойств нелинейной динамики — «жёсткости» [1,4,5].
Обобщая сказанное, отметим, что вариантов проявлений качественных особенностей и характерных свойств нелинейной динамики много, они разноплановы как по условиям возникновения, так и по формам проявлений. Нерегулярность, как свойство такой динамики, — это скорее норма, чем исключение [2]. Причины столь сложной и непредсказуемой динамики нелинейной неавтономной системы заложены в структуре и составе внутренних параметрических взаимосвязей уравнения динамики . Одной из составляющих комплексного показателя таких взаимосвязей, несомненно, являются собственные числа функциональной матрицы Якоби. Анализ качественных особенностей динамики нелинейной неавтономной системы на основе декомпозиции искомых решений её уравнения динамики на составляющие, каждая из которых соответствует одному из собственных чисел функциональной матрицы Якоби, при сохранении логической и математической взаимосвязи между этими составляющими, отражает существо предлагаемого подхода к проведению соответствующих исследований и новой методологии.
Пример
Исследование качественных особенностей динамики нелинейной автономной системы на основе декомпозиции решений её уравнения динамики по собственным числам функциональной матрицы Якоби, соответствующей этому уравнению.
В форме уравнение динамики рассматриваемой нелинейной автономной системы имеет следующий вид:
где
После подстановки значений параметров, указанных в экспликации к уравнению , получили следующую унифицированную форму этого уравнения:
Уравнение , известное как уравнение «брюсселятора», уникально, поскольку качественные особенности его решений существенным образом зависят от соотношения между параметрами и [4]. При имеет место бифуркация Хопфа, в которой устойчивый предельный цикл, существующий при , переходит в устойчивую стационарную точку решения , соответствующую условию . Бифуркационное соотношение устанавливает границу для характера проявления особенностей и свойств решений уравнения в зависимости от соотношения между параметрами и . Бифуркационный характер динамики решений уравнения находит своё отражение в особенностях нестационарных свойств собственных чисел функциональной матрицы Якоби, соответствующей этому уравнению, а также в динамике элементов декомпозиции , этих решений по таким собственным числам. Выделение математических признаков и причинно-следственных соотношений указанной взаимосвязи и составляет методологическую основу предлагаемого подхода к исследованию качественных особенностей динамики рассматриваемой системы.
ополнив соответствующим образом матрицу выделенной линейной части уравнения за счёт матрицы с целью обеспечения её совпадения с матрицей Якоби получили следующее эквивалентное описание динамики системы [9,10]:
где и -нулевые коэффициенты в разложении регулярных составляющих решений в степенные ряды. Выполнив над уравнением вычислительную процедуру аналитической части аналитически-численного метода, в форме получили следующее описание искомых решений:
где -коэффициенты степенных рядов для регулярных составляющих искомых решений , вычисляемые по формулам , при и с использованием нестационарных собственных чисел функциональной матрицы Якоби уравнения .
Сформированные для искомых решений уравнения описания таковы, что не содержат сингулярных составляющих. Численная часть аналитически-численного метода на каждом шаге расчёта в заданном интервале исследования [0; 10] реализована по стандартной схеме. Результаты расчёта динамики системы с заданным предельным уровнем абсолютной локальной погрешности расчёта и предначальными условиями для случая, когда приведены на рис.1. Как видно из рисунка, динамику рассматриваемой нелинейной автономной системы характеризует устойчивый предельный цикл [4]. Характерной особенностью такой динамики является «жёсткость», т.е. чередование участков быстрого и медленного изменения характеристического уравнения . Однако, как видно из рис.2, принципиальное отличие нелинейного случая от линейного состоит в том, что показатель такого «удаления» не является константой, а с течением времени непрерывно меняется. В интервалах времени [3-4], [8-9], когда искомые решения изменяются достаточно быстро, нестационарный показатель , отражая эту особенность динамики, достигает сравнительно высоких значений, доходящих до 100 единиц. Начиная с момента времени , определяющего начало интервала с достаточно медленным изменением решений, показатель непрерывно уменьшается, принимая в интервале времени [4-8] значения, близкие к единице, указывая на отсутствие быстрых составляющих в этих решениях. Таким образом «жёсткость», как качественная особенность нелинейной динамики, характеризуется нестационарным показателем . Непрерывное изменение этого показателя, отражая существо нелинейной динамики, вскрывает основные принципы самоорганизации. Способ расчёта собственных чисел матрицы Якоби таков, что, начиная со второго шага расчёта, они являются функциями от вычисляемых приближённых начальных значений и искомых решений. В свою очередь, в соответствии с формулами , , эти собственные числа затем напрямую определяют динамические показатели искомых решений в конце текущего шага расчета. Таким образом, в пределах каждого шага расчёта управление динамикой, а значит и нестационарным показателем «жёсткости» этой динамики осуществляется посредством внутренних координатно-параметрических взаимосвязей самого уравнения . Эти внутренние взаимосвязи реализуются через динамические показатели решений , которые, с одной стороны, зависят от собственных чисел функциональной матрицы Якоби, а с другой стороны, определяют показатель «жёсткости» нелинейной динамики системы. Иначе говоря, нелинейная динамика системы обладает всеми признаками адаптивного управления, поскольку «жёсткость», являясь качественной особенностью и следствием этой динамики, порождается самой же этой динамикой, генерируя причинные соотношения через собственные числа матрицы Якоби.
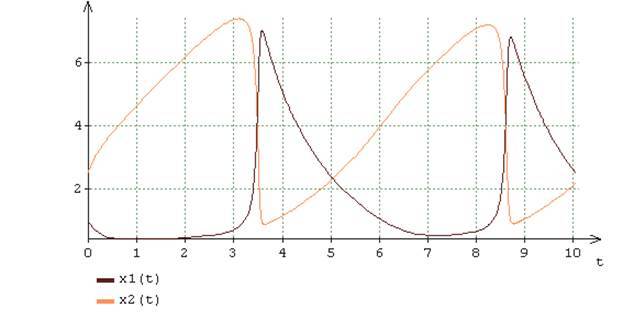
Рис.1. Приближённые решения уравнения при A = 2, B = 6 показателей искомых решений уравнения .
Необходимые для проведения анализа выявленного явления «жесткости» результаты расчёта представлены на рис. 2-4. Эти результаты соответствуют реализованной на основе представлений -, при и декомпозиции решений уравнений по собственным числам функциональной матрицы Якоби. Так, например, на рис.2 приведены графики изменения вещественных и мнимых частей нестационарных собственных чисел функциональной матрицы Якоби уравнения . Согласно этим графикам, «жёсткость», как и в случае линейной автономной системы, характеризуется удалением друг от друга абсолютных значений вещественных частей максимального и минимального по модулю корней
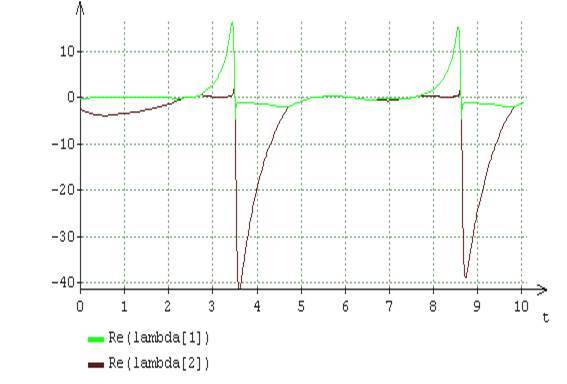
(а)

(б)
Рис.2. Динамика вещественных (а) и мнимых (б) частей собственных чисел функциональной матрицы Якоби при A= 2, B = 6
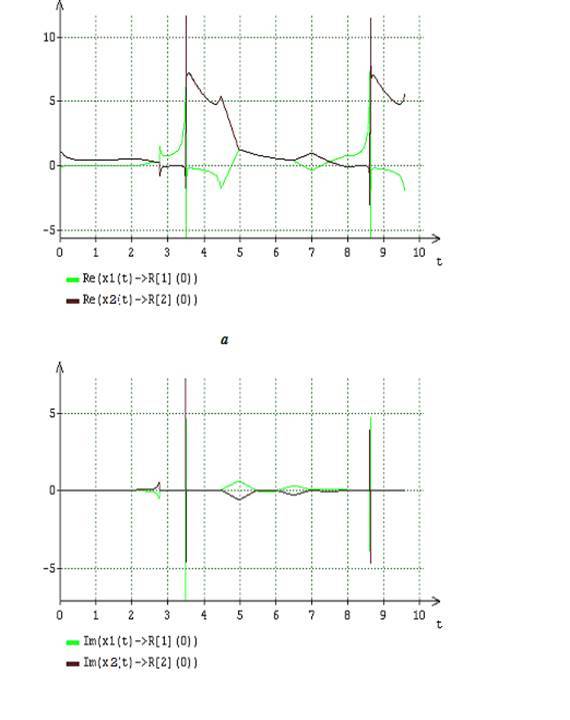
Рис.3. Динамика вещественных (а) и мнимых(б) частей двух составляющих (13), искомого решения уравнения (16) при A = 2, B = 6
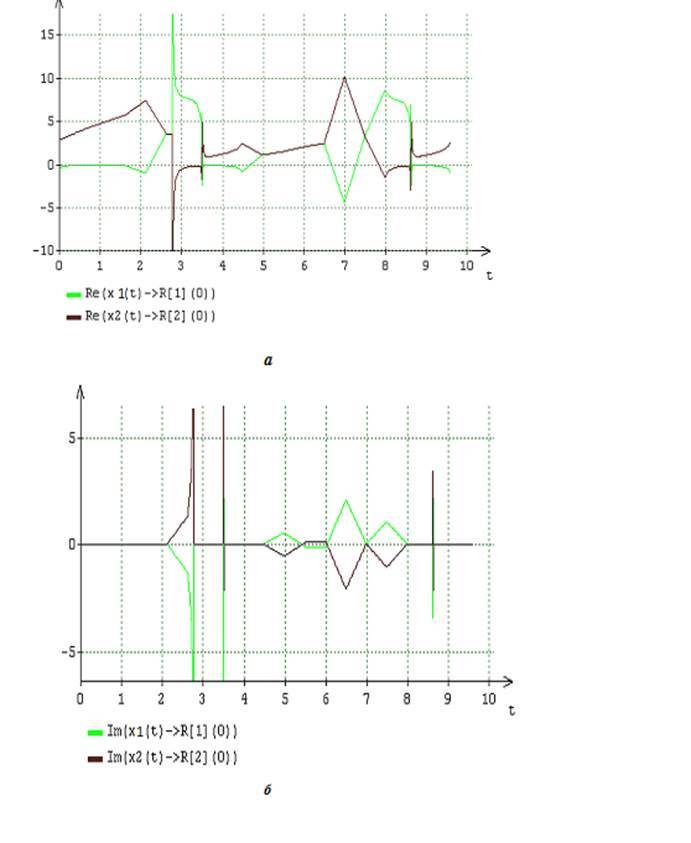
Рис.4. Динамика вещественных (а) и мнимых (б) частей двух составляющих (13), искомого решения уравнения (16) при A = 2, B = 6
Характеризуя изменение в заданном интервале исследования [0-10] нестационарных собственных чисел функциональной матрицы Якоби, в качестве интегрального показателя такого изменения можно рассматривать нестационарные свойства двух взаимосвязанных функций . Для последующих рассуждений необходимо отметить характерное свойство этих функций, которое однозначно соответствуют проявляемым в существующем устойчивом предельном цикле особенностям динамики решений уравнения . Ключевым признаком такого соответствия, согласно рис.2, служит характерное свойство функций , выражающееся в регулярном характере чередования действительных и комплексных областей их допустимых значений. Это чередование в устойчивом предельном цикле, отражая специфику динамических свойств решений уравнения , является информационным показателем выявления условий возникновения бифуркации Хопфа. Иначе говоря, в качестве информационного показателя бифуркации, как процесса скачкообразного изменения качественных динамических свойств системы, можно рассматривать сам факт возникновения или исчезновения в заданном интервале исследования ограниченных интервалов времени, в пределах которых множество значений функций принадлежит множеству действительных чисел. Для уравнения математический признак существования или отсутствия таких интервалов времени отражает условие реализации бифуркационного соотношения параметров системы: .
Нестационарный характер собственных чисел функциональной матрицы Якоби, посредством взаимосвязи, описываемой формулами , и равенствами , направленным образом обусловливает динамику полученных в результате декомпозиции по этим числам составляющих , каждого из искомых решений уравнения . В интервалах времени [0 -2,5] и [4 -6,5], когда, согласно результатам, представленным на рис.1,3,4, решения изменяются медленно, составляющие , каждого из искомых решений обладают вещественными и мнимыми частями и в сумме, согласно равенству ,, определяют качественное содержание и приближённые значения этих решений. Численные значения составляющих , искомых решений таковы, что их вклад в вычисляемые на каждом шаге расчёта приближённые значения решений почти соизмерим. Иначе говоря, в интервалах медленного изменения решений уравнения среди их составляющих отсутствует какое-либо доминирование во влиянии на формирование динамических показателей решений.
В интервалах времени [3 — 4] и [7 — 8], когда, как следует из рис.1,3,4, решения уравнения , изменяются быстро, их составляющие , , за исключением сравнительно малой окрестности точек, соответствующих изменению знака вещественных частей собственных чисел функциональной матрицы Якоби, обладают только вещественными частями. Такой характер численных значений составляющих , решений полностью соответствует характеру изменения нестационарных собственных чисел функциональной матрицы Якоби, приведённому на рис.2. Анализируя влияние и взаимодействие составляющих решений , на динамические показатели решений, необходимо отметить явно выраженный признак доминирования одной составляющей над другой. Это доминирование для каждого из искомых решений проявляется по-своему. Так, для первого из искомых решений , согласно рис.3, в интервалах быстрого изменения его показателей явно доминирует вторая составляющая, , согласно рис.4, картина принципиально иная, характеризуется переменным доминированием то первой составляющей , то второй . Таким образом, качественным признаком существования устойчивого предельного цикла для решения уравнения служит наличие интервалов времени, в пределах которых между двумя составляющими , решений явно прослеживается доминирование одной над другой.
Принимая во внимание выделенные ранее взаимосвязи качественных особенностей динамики решений уравнения и информационного содержания показателей, связанных с декомпозицией этих решений, представляют интерес результаты расчёта, приведённые на рис.5-8. Эти результаты соответствую расчёту рассматриваемой нелинейной автономной системы в случае, когда в её уравнении динамики
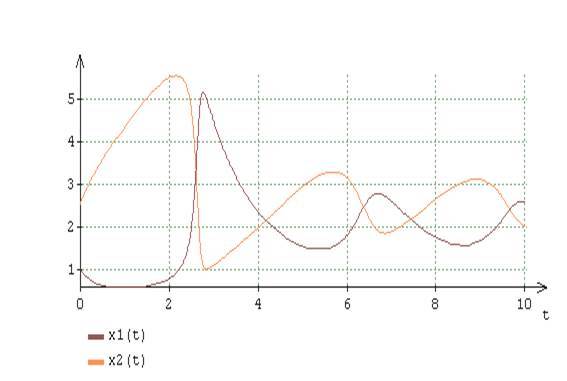
Рис.5. Приближённые решения уравнения (16) при A = 2, B = 5
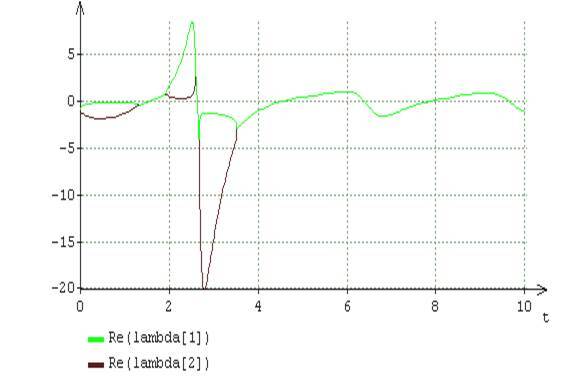
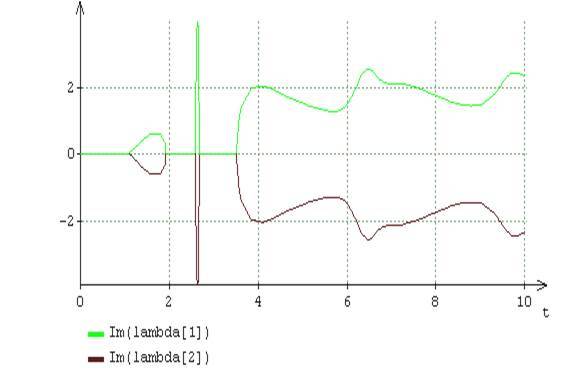
Рис.6. Динамика вещественных (а) и мнимых (б) частей собственных чисел функциональной матрицы Якоби уравнения (16) при A = 2, B = 5
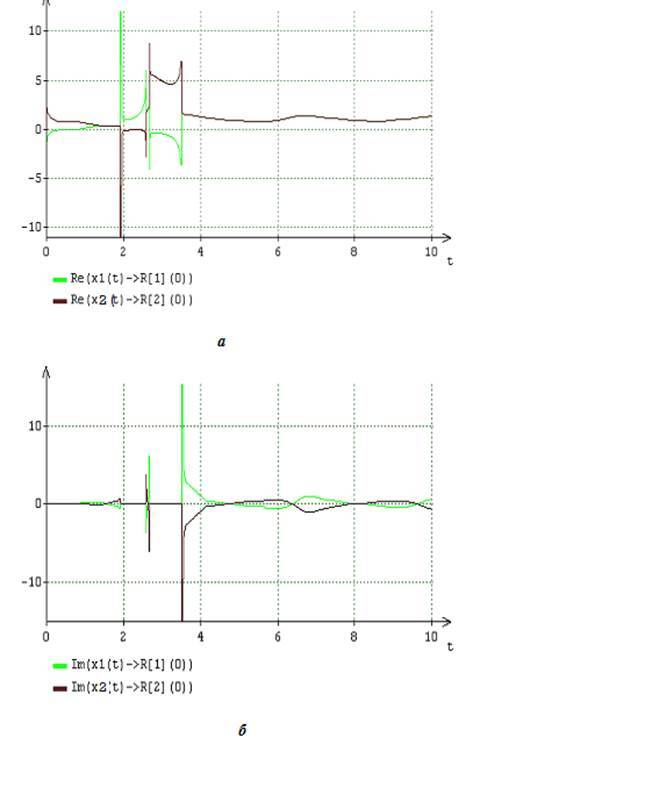
Рис.7. Динамика вещественных (а) и мнимых (б) частей двух составляющих (13) искомого решения уравнения (16) при A = 2, B = 5
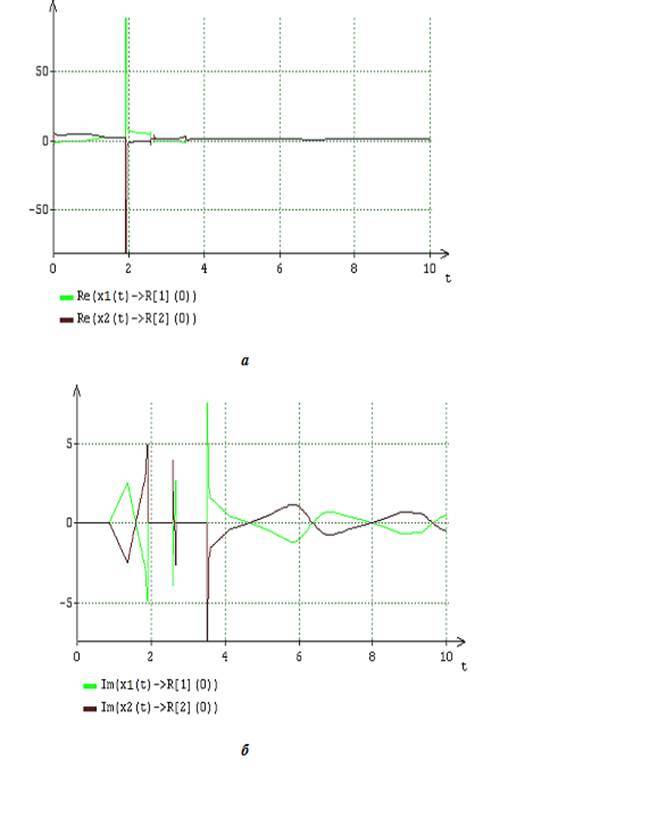
Рис.8. Динамика вещественных (а) и мнимых (б) частей двух составляющих (13) искомого решения уравнения (16) при A = 2, B = 5
Предначальные условия, интервал исследования и предельный уровень абсолютной локальной погрешности расчёта те же, что и для рассмотренного ранее случая
На рис.5 приведены приближённые решения уравнения при и согласно этим результатам действительно имеет место бифуркация Хопфа, когда при устойчивый предельный цикл, существование которого определяет условие , переходит в устойчивую стационарную точку решения с показателями: . Качественное изменение характера динамики системы вследствие такой бифуркации находит своё отражение, как видно на рис.6-8, и в изменениях характерных свойств динамики нестационарных собственных чисел функциональной матрицы Якоби и в описываемых равенствами при и двух составляющими каждого из искомых решений.
На рис.6 представлены графики изменения вещественных и мнимых частей собственных чисел функциональной матрицы Якоби при и . Как видно на рис.6, после момента времени собственные числа функциональной матрицы Якоби имеют исключительно комплексный характер. Согласно рис.2, в устойчивом предельном цикле эти собственные числа принимают как комплексные, так и действительные значения. Таким образом, математическим признаком бифуркации Хопфа, обусловливающей переход решений уравнения от устойчивого предельного цикла к устойчивой стационарной точке , служит отсутствие, после непродолжительного переходного процесса, действительных чисел среди значений собственных чисел , функциональной матрицы Якоби.
Как видно на рис.5, в результате бифуркации из состава характерных свойств искомого решения уравнения исчезает «жесткость». Существование этого свойства динамики системы в устойчивом предельном цикле неразрывно связано с чередованием по интервалов, когда нестационарные собственные числа функциональной матрицы Якоби принимают то действительные, то комплексные значения. При переходе к устойчивой стационарной точке решения уравнения , , вследствие изменения внутренних координатно-параметрических взаимосвязей указанное чередование исчезает. Таким образом, исчезновение «жёсткости» из состава качественных особенностей решений уравнения это следствие отсутствия, после непродолжительного переходного процесса, действительных чисел среди значений собственных чисел , функциональной матрицы Якоби.
Во взаимосвязи с отмеченными особенностями представляет интерес изменение в бифуркации Хопфа характера взаимодействия составляющих, искомых решений уравнения , соответствующих собственным числам функциональной матрицы Якоби. Сравнительный анализ результатов, представленных на рис.3,4 и рис.7,8, показывает, что одним из условий перехода от устойчивого предельного цикла решения к устойчивой стационарной точке служит качественное изменение характера взаимодействия составляющих , искомых решений . В устойчивом предельном цикле решения характерно наличие интервалов времени, в которых влияние составляющих декомпозиции , на динамические показатели решений сопряжено с доминированием одной составляющей над другой. Рис.7,8 указывают на отсутствие такой качественной особенности для случая устойчивой стационарной точки решения. Таким образом, математическим признаком бифуркации Хопфа, вызванной переходом искомых решений уравнения от устойчивого предельного цикла к устойчивой стационарной точке , служит исключение какого-либо доминирования среди составляющих , при формировании динамических показателей искомых решений.
Список литературы
- Данилов Л.В., Матханов П.Н., Филиппов Е.С. Теория нелинейных электрических цепей. – Л.: Энергоатомиздат, 1990. – 256 с.
- Хакен Г. Синергетика. Иерархия неустойчивостей в самоорганизующихся системах и устройствах. – М.: Мир, 1985. – 423 с.
- Кроновер Р.М. Фракталы и хаос в динамических системах. Основы теории. –М.: Постмаркет, 2000. –352 с.
- Хайрер Э., Нерсетт С., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Нежёсткие задачи / Пер. с англ. И.А. Кульчицкой, С.С. Филиппова (ред.) – М.: Мир, 1990. –512 с.
- Заславский Г.М., Сагдеев Р.З., Усиков Д.А., Черников А.А. Слабый хаос и квазирегулярные структуры.- М.: Наука, 1991.-240с.
- Егоренков Д.Л., Фрадков А.Л., Харламов В.Ю. Основы математического моделирования с примерами на языке MATLAB / Изд-во
БГТУ. – СПб., 1996. –192 с. - Андриевский Б.Р. Анализ систем в пространстве состояний. – СПб.: ИПМаш РАН, 1997. – 206 с.
- Афанасьев В.Н., Колмановский В.Б., Носов В.Р. Математическая теория конструирования систем управления. –М.: Высшая шк., 1989. – 447 с.
- Бычков Ю.А., Щербаков С.В. Аналитически-численный метод расчета динамических систем. – Издание второе, дополненное. СПб., Энергоатомиздат, Санкт-Петербургское отделение, 2002. – 368 с.
- Бычков Ю.А., Щербаков С.В. Аналитический и численный расчёт детерминированных нелинейных моделей динамических систем с сосредоточенными и распределёнными нестационарными параметрами. Издание второе, переработанное и дополненное. СПб.: Изд-во СПбГЭТУ "ЛЭТИ", 2014. — 388с.
Комментарии (6)

RPG18
13.02.2017 11:39+1Если бы Бычков Ю.А. не читал бы мне курс ТОЭ, то я бы не понял для чего все это. Может быть имеет смысл в начале написать вводную, где и для чего это применяется.

saluev
13.02.2017 12:47+5Вдруг подумал, что для бескомпромиссного уничтожения Хабра достаточно включить его в список ВАК.

Smorodov
14.02.2017 16:00Сюда бы картинок и анимаций, чтобы иллюстрировать зачем все это надо и мотивировать на чтение.


IliaSafonov
Что-то почти все формулы испортились. Это проблема с постом или с движком?
Surgun
Хороший вопрос. В предпросмотре все корректно, но после F5 большая часть формул не отображается. Формат выражений 5 раз перепроверил.
Surgun
Разобрался: комбинация Markdown и MathJax требуют более аккуратного использования символов _ и *