В статье мы пойдём по другому пути. Начнём с самой простой конфигурации — одного нейрона с одним входом и одним выходом, без активации. Далее будем маленькими итерациями усложнять конфигурацию сети и попробуем выжать из каждой из них разумный максимум. Это позволит подёргать сети за ниточки и наработать практическую интуицию в построении архитектур нейросетей, которая на практике оказывается очень ценным активом.
Иллюстративный материал
Популярные приложения нейросетей, такие как классификация или регрессия, представляют собой надстройку над самой сетью, включающей два дополнительных этапа — подготовку входных данных (выделение признаков, преобразование данных в вектор) и интерпретацию результатов. Для наших целей эти дополнительные стадии оказываются лишними, т.к. мы смотрим не на работу сети в чистом виде, а на некую конструкцию, где нейросеть является лишь составной частью.
Давайте вспомним, что нейросеть является ничем иным, как подходом к приближению многомерной функции Rn -> Rn. Принимая во внимания ограничения человеческого восприятия, будем в нашей статье приближать функцию на плоскости. Несколько нестандартное применение нейросетей, но оно отлично подходит для цели иллюстрации их работы.
Фреймворк
Для демонстрации конфигураций и результатов предлагаю взять популярный фреймворк Keras, написанный на Python. Хотя вы можете использовать любой другой инструмент для работы с нейросетями — чаще всего различия будут только в наименованиях.
Самая простая нейросеть
Самой простой из возможных конфигураций нейросетей является один нейрон с одним входом и одним выходом без активации (или можно сказать с линейной активацией f(x) = x):

N.B. Как видите, на вход сети подаются два значения — x и единица. Последняя необходима для того, чтобы ввести смещение b. Во всех популярных фреймворках входная единица уже неявно присутствует и не задаётся пользователем отдельно. Поэтому здесь и далее будем считать, что на вход подаётся одно значение.
Несмотря на свою простоту эта архитектура уже позволяет делать линейную регрессию, т.е. приближать функцию прямой линией (часто с минимизацией среднеквадратического отклонения). Пример очень важный, поэтому предлагаю разобрать его максимально подробно.
import matplotlib.pyplot as plt
import numpy as np
# накидываем тысячу точек от -3 до 3
x = np.linspace(-3, 3, 1000).reshape(-1, 1)
# задаём линейную функцию, которую попробуем приблизить нашей нейронной сетью
def f(x):
return 2 * x + 5
f = np.vectorize(f)
# вычисляем вектор значений функции
y = f(x)
# создаём модель нейросети, используя Keras
from keras.models import Sequential
from keras.layers import Dense
def baseline_model():
model = Sequential()
model.add(Dense(1, input_dim=1, activation='linear'))
model.compile(loss='mean_squared_error', optimizer='sgd')
return model
# тренируем сеть
model = baseline_model()
model.fit(x, y, nb_epoch=100, verbose = 0)
# отрисовываем результат приближения нейросетью поверх исходной функции
plt.scatter(x, y, color='black', antialiased=True)
plt.plot(x, model.predict(x), color='magenta', linewidth=2, antialiased=True)
plt.show()
# выводим веса на экран
for layer in model.layers:
weights = layer.get_weights()
print(weights)
Как видите, наша простейшая сеть справилась с задачей приближения линейной функции линейной же функцией на ура. Попробуем теперь усложнить задачу, взяв более сложную функцию:
def f(x):
return 2 * np.sin(x) + 5
Опять же, результат вполне достойный. Давайте посмотрим на веса нашей модели после обучения:
[array([[ 0.69066334]], dtype=float32), array([ 4.99893045], dtype=float32)]Первое число — это вес w, второе — смещение b. Чтобы убедиться в этом, давайте нарисуем прямую f(x) = w * x + b:
def line(x):
w = model.layers[0].get_weights()[0][0][0]
b = model.layers[0].get_weights()[1][0]
return w * x + b
# отрисовываем результат приближения нейросетью поверх исходной функции
plt.scatter(x, y, color='black', antialiased=True)
plt.plot(x, model.predict(x), color='magenta', linewidth=3, antialiased=True)
plt.plot(x, line(x), color='yellow', linewidth=1, antialiased=True)
plt.show()Всё сходится.
Усложняем пример
Хорошо, с приближением прямой всё ясно. Но это и классическая линейная регрессия неплохо делала. Как же захватить нейросетью нелинейность аппроксимируемой функции?
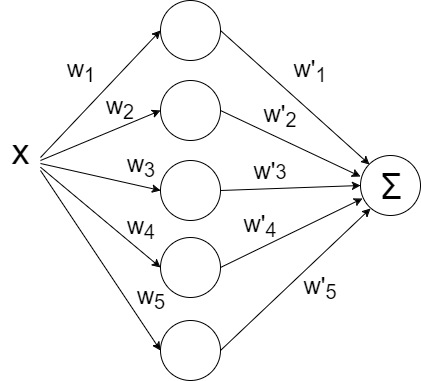
Давайте попробуем накидать побольше нейронов, скажем пять штук. Т.к. на выходе ожидается одно значение, придётся добавить ещё один слой к сети, который просто будет суммировать все выходные значения с каждого из пяти нейронов:
def baseline_model():
model = Sequential()
model.add(Dense(5, input_dim=1, activation='linear'))
model.add(Dense(1, input_dim=5, activation='linear'))
model.compile(loss='mean_squared_error', optimizer='sgd')
return modelЗапускаем:
И… ничего не вышло. Всё та же прямая, хотя матрица весов немного разрослась. Всё дело в том, что архитектура нашей сети сводится к линейной комбинации линейных функций:
f(x) = w1' * (w1 * x + b1) +… + w5' (w5 * x + b5) + b
Т.е. опять же является линейной функцией. Чтобы сделать поведение нашей сети более интересным, добавим нейронам внутреннего слоя функцию активации ReLU (выпрямитель, f(x) = max(0, x)), которая позволяет сети ломать прямую на сегменты:
def baseline_model():
model = Sequential()
model.add(Dense(5, input_dim=1, activation='relu'))
model.add(Dense(1, input_dim=5, activation='linear'))
model.compile(loss='mean_squared_error', optimizer='sgd')
return modelМаксимальное количество сегментов совпадает с количеством нейронов на внутреннем слое. Добавив больше нейронов можно получить более точное приближение:
Дайте больше точности!
Уже лучше, но огрехи видны на глаз — на изгибах, где исходная функция наименее похожа на прямую линию, приближение отстаёт.
В качестве стратегии оптимизации мы взяли довольно популярный метод — SGD (стохастический градиентный спуск). На практике часто используется его улучшенная версия с инерцией (SGDm, m — momentum). Это позволяет более плавно поворачивать на резких изгибах и приближение становится лучше на глаз:
# создаём модель нейросети, используя Keras
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
def baseline_model():
model = Sequential()
model.add(Dense(100, input_dim=1, activation='relu'))
model.add(Dense(1, input_dim=100, activation='linear'))
sgd = SGD(lr=0.01, momentum=0.9, nesterov=True)
model.compile(loss='mean_squared_error', optimizer=sgd)
return modelУсложняем дальше
Синус — довольно удачная функция для оптимизации. Главным образом потому, что у него нет широких плато — т.е. областей, где функция изменяется очень медленно. К тому же сама функция изменяется довольно равномерно. Чтобы проверить нашу конфигурацию на прочность, возьмём функцию посложнее:
def f(x):
return x * np.sin(x * 2 * np.pi) if x < 0 else -x * np.sin(x * np.pi) + np.exp(x / 2) - np.exp(0)Увы и ах, здесь мы уже упираемся в потолок нашей архитектуры.
Дайте больше нелинейности!
Давайте попробуем заменить служивший нам в предыдущих примерах верой и правдой ReLU (выпрямитель) на более нелинейный гиперболический тангенс:
def baseline_model():
model = Sequential()
model.add(Dense(20, input_dim=1, activation='tanh'))
model.add(Dense(1, input_dim=20, activation='linear'))
sgd = SGD(lr=0.01, momentum=0.9, nesterov=True)
model.compile(loss='mean_squared_error', optimizer=sgd)
return model
# тренируем сеть
model = baseline_model()
model.fit(x, y, nb_epoch=400, verbose = 0)
Инициализация весов — это важно!
Приближение стало лучше на сгибах, но часть функции наша сеть не увидела. Давайте попробуем поиграться с ещё одним параметром — начальным распределением весов. Используем популярное на практике значение 'glorot_normal' (по имени исследователя Xavier Glorot, в некоторых фреймворках называется XAVIER):
def baseline_model():
model = Sequential()
model.add(Dense(20, input_dim=1, activation='tanh', init='glorot_normal'))
model.add(Dense(1, input_dim=20, activation='linear', init='glorot_normal'))
sgd = SGD(lr=0.01, momentum=0.9, nesterov=True)
model.compile(loss='mean_squared_error', optimizer=sgd)
return modelУже лучше. Но использование 'he_normal' (по имени исследователя Kaiming He) даёт ещё более приятный результат:
Как это работает?
Давайте сделаем небольшую паузу и разберёмся, каким образом работает наша текущая конфигурация. Сеть представляет из себя линейную комбинацию гиперболических тангенсов:
f(x) = w1' * tanh(w1 * x + b1) +… + w5' * tanh(w5 * x + b5) + b
# с помощью матрицы весом моделируем выход каждого отдельного нейрона перед суммацией
def tanh(x, i):
w0 = model.layers[0].get_weights()
w1 = model.layers[1].get_weights()
return w1[0][i][0] * np.tanh(w0[0][0][i] * x + w0[1][i]) + w1[1][0]
# рисуем функцию и приближение
plt.scatter(x, y, color='black', antialiased=True)
plt.plot(x, model.predict(x), color='magenta', linewidth=2, antialiased=True)
# рисуем разложение
for i in range(0, 10, 1):
plt.plot(x, tanh(x, i), color='blue',
linewidth=1)
plt.show()На иллюстрации хорошо видно, что каждый гиперболический тангенс захватил небольшую зону ответственности и работает над приближением функции в своём небольшом диапазоне. За пределами своей области тангенс сваливается в ноль или единицу и просто даёт смещение по оси ординат.
За границей области обучения
Давайте посмотрим, что происходит за границей области обучения сети, в нашем случае это [-3, 3]:
Как и было понятно из предыдущих примеров, за границами области обучения все гиперболические тангенсы превращаются в константы (строго говоря близкие к нулю или единице значения). Нейронная сеть не способна видеть за пределами области обучения: в зависимости от выбранных активаторов она будет очень грубо оценивать значение оптимизируемой функции. Об этом стоит помнить при конструировании признаков и входных данный для нейросети.
Идём в глубину
До сих пор наша конфигурация не являлась примером глубокой нейронной сети, т.к. в ней был всего один внутренний слой. Добавим ещё один:
def baseline_model():
model = Sequential()
model.add(Dense(50, input_dim=1, activation='tanh', init='he_normal'))
model.add(Dense(50, input_dim=50, activation='tanh', init='he_normal'))
model.add(Dense(1, input_dim=50, activation='linear', init='he_normal'))
sgd = SGD(lr=0.01, momentum=0.9, nesterov=True)
model.compile(loss='mean_squared_error', optimizer=sgd)
return modelМожете сами убедиться, что сеть лучше отработала проблемные участки в центре и около нижней границы по оси абсцисс:
N.B. Слепое добавление слоёв не даёт автоматического улучшения, что называется из коробки. Для большинства практических применений двух внутренних слоёв вполне достаточно, при этом вам не придётся разбираться со спецэффектами слишком глубоких сетей, как например проблема исчезающего градиента. Если вы всё-таки решили идти в глубину, будьте готовы много экспериментировать с обучением сети.
Количество нейронов на внутренних слоях
Просто поставим небольшой эксперимент:
Начиная с определённого момента добавление нейронов на внутренние слои не даёт выигрыша в оптимизации. Неплохое практическое правило — брать среднее между количеством входов и выходов сети.
Количество эпох
Выводы
Нейронные сети — это мощный, но при этом нетривиальный прикладной инструмент. Лучший способ научиться строить рабочие нейросетевые конфигурации — начинать с более простых моделей и много экспериментировать, нарабатывая опыт и интуицию практика нейронных сетей. И, конечно, делиться результатами удачных экспериментов с сообществом.
Комментарии (52)

BelBES
22.02.2017 21:29+8Многие материалы по нейронным сетям сразу начинаются с демонстрации довольно сложных архитектур. При этом самые базовые вещи, касающиеся функций активаций, инициализации весов, выбора количества слоёв в сети и т.д. если и рассматриваются, то вскользь. Получается начинающему практику нейронных сетей приходится брать типовые конфигурации и работать с ними фактически вслепую.
А мне вот наоборот всегда казалось, что многие с энтузиазмом берутся за написание курса по нейронным сетям, начинают с азов, и на том энтузиазм заканчивается. В итоге есть куча статей о том, как работает Персептрон Розенблата и какой-нибудь Многослойный Персептрон, а вот чего посложнее — это редкость.
Разве что наш кумир Карпати зажигательно рассказвыает в своем блоге про всякие современные штуки в области нейросайнса) Но основным источником знаний все равно остается arxiv-sanity.com )
kdenisk
22.02.2017 23:26+1Спасибо за комментарий. Вообще в математике, а нейросети безусловно являются частью прикладной математики, существует проблема передачи определённого типа знаний. Вы можете рассказать человеку теорию, а можете дать рецепт решения конкретной задачи, обосновав его с научной точки зрения. Но есть срединное знание — математическая интуиция — которая позволяет человеку создавать те самые рецепты. И его невозможно передать через письменные источники, оно появляется индивидуально в процессе мышления и попыток применить теорию к практическим задачам.
В нейросетях сейчас та же ситуация — есть теория, объясняющая основные принципы нейросетей, вводящая терминологию, очерчивающая круг проблем, которые решают с помощью НС и т.д. Есть готовые рецепты — когда исследователь проанализировал определённый круг задач, нашёл рабочие подходы и изложил их, к примеру, в научной статье.
Представленный материал, строго говоря, не относится ни к тому, ни к другому. Это попытка построить серию модельных примеров для нейросетей, которые можно покрутить, повертеть, подёргать и наработать немного той самой интуиции, которая будет полезна в дальнейшем.

BubaVV
23.02.2017 00:50+3Бодрое начало, жду продолжения. Важный момент: надо помнить об «объеме памяти» сети. Если нейронов много, то весь набор данных может «запомниться» в весах связей и получим переобучение с идеальным повторением тренировочного набора, но абсолютной беспомощностью на других входных данных.

alex_blank
23.02.2017 05:46+5f(x) = w1' * tanh(w1 * x + b1) +… + w5' * tanh(w5 * x + b5) + bСделал визуализатор — можно потаскать за точки и увидеть эту аппроксимацию наглядно. Фиолетовые линии это линейные функции (
w1 * x + b1), оранжевые — взвешенные гиперболические тангенсы (w * tanh (..)). Красное — итоговая сумма.
Веса у тангенсов задаются расстоянием между точками (чем больше, тем больше вес):


KiloLeo
25.02.2017 00:05+1Очень наглядно и полезно почувствовать поведение аппроксиматора, даже если теоретически всё понятно. Студентам на лабораторку!

superkrivoy
23.02.2017 09:46+1Спасибо, за возможность: "покрутить, подергать". Я думаю менно такой подход и будет интересен многим новичкам в НС.

bapcyk
23.02.2017 09:46+1Насколько я неправ, полагая что нейронные сети — это метод подгонки коэффициентов некого полинома или рекуррентого уравнения, в случае обратных связей? Такое чувство, что за словом нейронная сеть ничего нового не стоит, кроме способа подбора этих коэффициентов? Минимизация, может быть что-то из области регрессионного анализа, нет?

kdenisk
23.02.2017 10:24+2В случае с приближением полиномом у вас на руках довольно бедное семейство функций. Допустим если окололинейную зависимость приближать полиномом двенадцатой степени, то наверняка итоговая аппроксимация будет не самой удачной.
В случае с даже простыми нейросетями у вас на руках куда более богатое семейство функций, позволяющее хорошо приближать даже неравномерно распределённые нелинейности и нетривиальные корреляции в данных (если речь идёт о нескольких входах сети).
Получаем более мощный инструмент для аппроксимации, но и обучать его намного сложнее. Собственно солидная доля исследований в области нейросетей посвящена практике правильного обучения и борьбы с разными возникающими спецэффектами.
Итого, отвечая на ваш вопрос. Математический арсенал, задействованный в НС, пришёл из методов оптимизации и известен уже давно. А вот то, как он применяется для решения практических задач — это очень новые подходы, большинство из которых разработано в последние 5-8 лет. В сочетании со ставшим сильно более доступным железом это открывает кучу возможностей в самых разных областях — от компьютерного зрения и распознавания речи до машинного перевода и генерации текста машиной.

Korogodin
24.02.2017 02:24+1Здорово, как будто сам поигрался с фреймворком. Я одного не понял, какая задача стояла? Обвести известную кривую?

kdenisk
24.02.2017 12:22+2Спасибо! Приближение кривой на плоскости — это модельный пример, позволяющий более наглядно показать результат работы сети. Ведь если брать, к примеру, классический сет для регрессии с ценами домов, то единственным наглядным результатом работы сети является среднеквадратичное отклонение. И меняя конфигурацию сети человек смотрит в какую сторону меняется это одно единственное число. Что при этом происходит внутрях нейросети остаётся сильно за кадром.
Наше мышление построено по принципу «от частного к общему», поэтому не стоит недооценивать важность простых иллюстративных примеров. Если этот принцип работает при изучении языка, математики, физики и т.д., то почему нейросети — исключение?
Korogodin
24.02.2017 12:31-1Без контекста дальшейшего использования возникает вопрос «Зачем так сложно?» Чтобы построить график известной функции… можно взять и построить график известной функции)) Что дает обучение на таком примере? Возможность интерполировать кривую между точек?
Может в качестве выборки для обучения и для последующей обработки брал набор из зашумленных кривых? Хотя бы результат будет нетривиален =)
kdenisk
24.02.2017 16:04>> построить график известной функции… можно взять и построить график известной функции
Не придирайтесь. Пример модельный и подбирался по принципу иллюстративности, чтобы наглядно показать как конфигурация сети влияет на результат.
>> Может в качестве выборки для обучения и для последующей обработки брал набор из зашумленных кривых?
Дельное предложение, однозначно стоит попробовать.
Korogodin
24.02.2017 22:09-1Я и не думал придираться, и сарказма у меня ноль.
Ваша статья была очень интересна. Я наглядно увидел как пользоваться фреймворком, впервые встретил простую и наглядную интерпретацию результата через сумму по функциям активации и получил удовольствие. Тут есть наглядные ответы на вопрос «как?», но я, будучи читатетелем с околонулевым бэкграундом в нейросетях, сразу задался вопросом «зачем?». Его и транслирую вам.
То есть я в целом понимаю, что потом всё это как-то используется для решения задач классификации. Но связи пока не уловил.
alex_blank
25.02.2017 10:20+2> Чтобы построить график известной функции
Так а вы представьте, что функция не известна. Есть большой набор данных, и нужно найти относительно простую функцию, которая наиболее хорошо их описывает. Алгоритм обучения подгоняет коэффициенты, пока такое приближение не будет найдено с достаточной степенью соответствия.

Korogodin
25.02.2017 12:15Это уже интереснее, но непонятно, чем НС будет лучше других методов. Например, МНК.
Из того, что бросается в глаза — НС не просто найдет среднее по точкам, а предложит аппроксимацию в виде функции, определенной на всем континууме.
Dark_Daiver
25.02.2017 19:14Если под МНК вы имеете ввиду линейный МНК (линейная ф-ия под квадратом), то ИНС, как правило, могут работать с нелинейными зависимости.

kdenisk
25.02.2017 11:49+1Понял. Интернет — коварная штука и не видя интонаций я был в полной уверенности, что вы меня подтролливаете :)
Очень кратко на ваш вопрос я отвечал ниже, см. комментарий. Более развёрнуто имеет смысл смотреть на примерах конкретных задач, например классификации или регрессии. Мне кажется будет интересно сделать статью, где подробно разобрать типовые примеры из репозитория Keras, а заодно посмотреть как нейросеть встраивается в общий конвейер решения задачи машинного обучения. Как считаете, интересен будет такой материал?
Korogodin
25.02.2017 12:11+1Да, конечно! Мне очень нравится ваш формат пошагового усложнения, полный «эффект присутствия».

ntkj666
24.02.2017 02:26А что такое "эпохи"?

Korogodin
24.02.2017 02:29Могу предположить, что алгоритм обучения рекурентный. Видимо эпохи — число итераций.

kdenisk
24.02.2017 11:52+1Это важно! В терминологии нейросетей принято разделять «эпохи» и «итерации».
Итерация — это прогон одного примера (в общем случае n_batch примеров) через сеть в прямом и обратном направлениях (forward pass + backward pass).
Эпоха — это прогон всех примеров через сеть в обоих направлениях.
На практике, в большинстве случаев, количество итераций выставляют в единицу, т.е. за эпоху каждый пример прогоняется через сеть один раз. Имеет смысл поиграться с этим параметром, если данных мало. В этом случае вы фактически каждый пример дублируете в тренировочном сете n_iteration раз, не расходуя дополнительную память на дубли.
Korogodin
24.02.2017 22:21То есть, видимо, в основе обучения лежит какое-то градиентное, постепенное подкручивание параметров НС. Если я возьму один пример, прогоню через алгоритм обучения, то у меня как-то изменятся коэффициенты. «Сдвинутся» в некотором направлении, характерном для этого примера. Но ещё не упрутся в соответствующий экстремум. Тогда, если я опять прогоню этот же пример, то коэффициенты ещё «подвинутся». И так, пока мы не выйдем на некоторый предел. Каждая из этих попыток — итерация. Я правильно уловил?
Эпоха же отличается от итерации тем, что мы используем все доступные обучающие примеры. Они тоже все «подпинывают» коэффициенты в некотором направлении из некоторого начального состояния. Но в конечное, предельное состояние за один «пинок» коэффициенты не перевести. Таким образом, эпоха — это как итерация, только по совокупности примеров.
kdenisk
25.02.2017 11:36+1В общем и целом всё верно. Тут есть правда один важный момент: слишком много раз прогонять через сеть один пример или даже все примеры может быть чревато переобучением сети. Т.е. когда нейронка, как правильно выразился BubaVV выше, зазубривает тренировочный набор и перестаёт выдавать адекватный результат на новых данных.
Но как подобрать количество эпох, чтобы избежать переобучения? Алгоритмический вариант — использовать метод ранней остановки (early stopping). Идея в том, чтобы делать промежуточные промеры качества работы сети и если видим, что улучшений нет — останавливать обучение.
Иллюстрация одного из подходов (отсюда):

O_Ruby
24.02.2017 11:40+1Когда вы рассматриваете нейронную сеть с одним нейроном, вы пишите:
Хорошо, с приближением прямой всё ясно. Но это и классическая линейная регрессия неплохо делала.
Правильно я понял, что вы их разделяете? И, поправьте если не прав, не является ли НС с одним нейроном и линейной функцией активации ничем иным как линейной регрессией?
kdenisk
24.02.2017 11:44+1Суть фразы как раз в том, что сеть с одним нейроном и линейной активацией вырождается в линейную регрессию. Поэтому если мы хотим раскрыть настоящий потенциал нейросетей, то нужно двигаться дальше к нелинейным приближениям. Что и делается в следующем разделе.

v-ssch
24.02.2017 11:52Вопрос, зачем нужны нейронные сети?

kdenisk
24.02.2017 12:07+1Ваш вопрос тянет на отдельную статью :) Кратко — это хороший способ приближать сильно нелинейную многомерную функцию Rn -> Rn. Дальше вокруг нейросети выстраивается целый конвейер, который позволяет решать уйму задач.
На примере. Допустим вы хотите различать фотографии кошек и собак. Вы берёте исходное изображение, вытягиваете его в вектор (по строкам, например), в каждый элемент вектора записываете яркость пикселя, приведя к диапазону [-1, 1]. Для изображения 64x64 получаете 4096-мерный вектор. На выходе у вас двумерный вектор (1, 0) — кошка, (0, 1) — собака. Прогоняете через сеть размеченные изображения кошек и собак, она обучается. Если вы всё сделали правильно, то сеть сможет предсказывать кошка/собака для изображений, которые она никогда не видела.
Korogodin
24.02.2017 12:35Возникает вопрос, что такое «хороший»? Я про способ приближения функции. Ответ видимо лежит в области удобства алгоритма приближения, а не в области вычислительной простоты реализации результата?

O_Ruby
24.02.2017 13:49+1В одном курсе по машинному обучению нейронный сети рассматриваются как один из способов композиции алгоритмов наряду с адаптивным бустингом, бэггингом и т.д. и т.п… И основная идея, что несколько слабых классификаторов/регрессоров будут компенсировать ошибки друг друга и выдадут лучший результат. Вот так я понимаю слово «хороший». Поправьте, если ошибаюсь.
rPman
24.02.2017 14:13то есть, например, если вместо одной сети учить десять, с разной конфигурацией, алгоритмом обучения или просто начальная инициализация разная, а затем как то агрегировать их результаты, то итоговый результат будет 'лучше'?

O_Ruby
24.02.2017 15:06Я имел в виду, что нейросеть это уже сама по себе ансамбль. Про ансамбли сетей я не читал и я не рискну давать оценку, будут ли результаты 'лучше'. А вот ансамбль из принципиально разных алгоритмов — популярный подход.

kdenisk
24.02.2017 16:01+1Так на практике и поступают. У нейросети тоже есть конфигурация в рамках которой она обучается (например, количество эпох). Вы можете выставить всё «на глазок», а можете написать метаалгоритм, который гоняет обучающий набор на разных настройках и выбирает лучший.
Другое дело, что обучение сети дело довольно ресурсоёмкое и прогонять несколько вариантов на обучающем наборе может быть непозволительно дорого. Для экспериментов берут срез реальной выборки и играются с ним, но не всегда хорошая конфигурация на срезе хорошо отработает на всём наборе. (Ещё и сохранить полезные свойства датасета при срезе — большое искусство.)
В общем, при работе с нейросетками сложно переоценить значение опыта, интуиции и удачи.

Korogodin
24.02.2017 14:20Пока разговор про классификацию даже не заходил ;) Пока что нейросеть —
это хороший способ приближать сильно нелинейную многомерную функцию Rn -> Rn.
Но есть ведь и другие способы приближения нелинейных функций. Хоть в ряд Тейлора её разложить, или в Фурье.
Давайте пока определимся хотя бы в чем состоит «хорошесть» по сравнению с другими способами, а потом уже будет наворачивать новые абстракции.
O_Ruby
24.02.2017 15:11+2А теперь представьте, что вы приближаете некоторую функцию, которая является разделяющей гиперплоскостью в некотором многомерном пространстве. Вот вам и классификация.

Dark_Daiver
25.02.2017 08:53+2>Но есть ведь и другие способы приближения нелинейных функций. Хоть в ряд Тейлора её разложить, или в Фурье.
Как правило у вас нет почти никакой информации о ф-ии которую вы хотите аппроксимировать, только ее значения в некоторых точках. В этих условиях взять туже производную для ряда Тейлора несколько проблематично.

kdenisk
24.02.2017 15:53+1Я практик, поэтому для меня ответ однозначен: для определённых задач, будучи правильно приготовленными, нейросети выдают результат лучше, чем другие инструменты. Есть ситуации, когда сеть не является оптимальным решением — по точности или по скорости. Используйте другой инструмент.
В теорию работы нейросетей погружаться можно и нужно, но в той мере, где это помогает практике, а не наоборот. Теоретизирование — удел больших корпораций, которые могут позволить себе сотрудничать с людьми уровня Джеффри Хинтона (например Google Brain / Google Translate). Простым смертным остаётся брать готовые рецепты от крупных компаний и исследователей, а затем пытаться применить их к своим задачам. Чаще всего это неплохо работает.
При этом я не умоляю значения опыта и интуиции каждого практика нейросетей, т.к. даже адаптировать готовый рецепт нужно уметь. Но и чувствовать сети, как ведущие исследователи из крупных университетов, вряд ли получится — у них просто больше ресурсов.

Korogodin
25.02.2017 12:29В данной статье после обучения отклик представляется как сумма гиперболических тангенсов от текущего входного значения.
Что будет, если разрабатывать НС для обработки коррелированных процессов, а не мгновенных значений? Нужно будет вводить дополнительные слои, которые будут отвечать за «память»?
kdenisk
25.02.2017 13:06+1Это интереснейшая тема, имеющая непосредственное отношение к компьютерной лингвистике (моей области интересов).
Для моделирования временных рядов используются рекуррентные нейронные сети (RNN) и их разновидность — сети с долгой краткосрочной памятью (LSTM RNN). Там как раз реализован механизм памяти, чтобы сеть не успевала забывать события, происходившие давно (с точки зрения обучения). Причём этот механизм также реализован с помощью простой нейросети.
Процесс обучения тоже перестраивается. Вместо тренировочного набора, мы бежим по временному ряду и в качестве входа сети берём значение ряда на шаге N, а в качестве выхода значение ряда на шаге N + 1. В результате сеть учится предсказывать S(N + 1) при входе S(N) и предшествующем контексте (выраженном в текущем состоянии сети), где S(1..M) — моделируемый временной ряд.
Если через такую сеть посимвольно прогнать большой объём текста, то она позволяет генерировать новый текст, причём практически идеальный с точки зрения грамматики. Правда совершенно бессмысленный :)
Если знаете английский, то есть просто-таки культовая статья на эту тему: The Unreasonable Effectiveness of Recurrent Neural Networks
Korogodin
25.02.2017 13:29Всё ближе к области моих интересов))
У меня есть процессы, которые принято описывать диффузионными марковскими случайными процессами. С ними хорошо работает математика, всё просто и понятно. Вот только настоящие процессы, как правило, плохо соответствуют модельным.
Преимущества нейросети — ей не нужно давать какие-то дополнительные математические модели процессов, она их сама определяет в процессе обучения.
Это и является моим основным интересом. Не обработка данных с помощью нейросети, а изучение самих процессов.
Из этой статьи я пришел к выводу, что НС разложит мои процессы по своему базису функций возбуждения. Соответственно, задача состоит не только в обучении некоторой НС с последующим изучением получившейся структуры, а в осмысленном выборе конфигурации НС! Так, чтобы потом эту НС можно было интерпретировать в удобных понятиях и функциях.

Korogodin
25.02.2017 14:31Если через такую сеть посимвольно прогнать большой объём текста, то она позволяет генерировать новый текст, причём практически идеальный с точки зрения грамматики. Правда совершенно бессмысленный :)
Тут возникает интересный практический вопрос. После обучения сеть знает «как надо». Можно ли её заставить анализировать вводимый текст и подсказывать в % выражении насколько он адекватен?
O_Ruby
25.02.2017 16:56Практический вопрос на практический вопрос: как формализовать понятие 'адекватен'?

Korogodin
25.02.2017 20:08В данном контексте — «вероятен». Соответствует нормам и правилам, выведенным ранее НС на этапе обучения.
Вспоминаем байесовский фильтр. У него есть экстраполяционная плотность вероятности, описывающая вероятности S(N+1). Есть ли нечто подобное для НС?

KiloLeo
25.02.2017 13:59+1Статья отличная, спасибо, всё повторил и пощупал. Правда, у меня результаты получались значительно хуже, хотя делал вроде бы всё также. Не понял почему.
И ещё замечание к заголовку. К глубоким архитектурам мы не приблизились и близко. Двуслойная сеть с одним входом это где-то на дальних подступах.



MooNDeaR
Прочел статью, в ожидании познать, как правильно выбрать функцию активации и узнать о различиях между ними. В итоге так и не узнал.
Да, в статье показана разность в работе двух функций активации, но о причинах такого поведения не сказано почти ни слова.
kdenisk
Разумное замечание и отличный вопрос. Чтобы на него ответить нужно готовить несколько другой пример и смотреть на активации/градиенты, наглядно демонстрируя достоинства и проблемы обеих функций. Выглядит как тема для статьи)