Во многих алгоритмах машинного обучения, в том числе в нейронных сетях, нам постоянно приходится иметь дело со взвешенной суммой или, иначе, линейной комбинацией компонент входного вектора. А в чём смысл получаемого скалярного значения?
В статье попробуем ответить на этот вопрос с примерами, формулами, а также множеством иллюстраций и кода на Python, чтобы вы могли легко всё воспроизвести и поставить свои собственные эксперименты.
Чтобы теория не отрывалась от реальных кейсов, возьмём в качестве примера задачу бинарной классификации. Есть датасет: m образцов, каждый образец — n-мерная точка. Для каждого образца мы знаем к какому классу он относится (зелёный или красный). Также известно, что датасет является линейно разделимым, т.е. существует n-мерная гиперплоскость такая, что зелёные точки лежат по одну сторону от неё, а красные — по другую.

К решению задачи поиска такой гиперплоскости можно подходить разными способами, например с помощью логистической регрессии (logistic regression), метода опорных векторов с линейным ядром (linear SVM) или взять простейшую нейросеть:

Рассмотрим подробную математику для прямой. Для общего случая гиперплоскости в n-мерном пространстве будет всё ровно тоже самое, с поправкой на количество компонент в векторах.

Прямая линия на плоскости задаётся тремя числами — :
или:
или:
Первые два коэффициента задают всё семейство прямых линий, проходящих через точку (0, 0). Соотношение между и определяет угол наклона прямой к осям.
Если , получаем линию, идущую под углом 45 градусов () к осям и и делящую первый/третий квадранты пополам.
Ненулевой коэффициент позволяет линии не проходить через ноль. При этом наклон к осям и не меняется. Т.е. задаёт семейство параллельных линий:

Геометрический смысл вектора — это нормаль к прямой :
(Если не учитывать смещение , то — это не более чем скалярное произведение двух векторов. Равенство нулю равносильно их ортогональности. Следовательно, — семейство векторов, ортогональных .)

P.S. Понятно, что таких нормалей бесконечно много, как и троек (w1, w2, b) задающих прямую. Если все три числа умножить на ненулевой коэффициент — прямая останется той же.
В общем случае n-мерного пространства, задаёт n-мерную гиперплоскость.
или:
или:
Если точка лежит на гиперплоскости, то
А что происходит с этой суммой, если точка не лежит на плоскости?
Гиперплоскость делит гиперпространство на два гиперподпространства. Так вот точки, находящиеся в одном из этих подпространств (условно говоря «выше» гиперплоскости), и точки, находящиеся в другом из этих подпространств (условно говоря «ниже» гиперплоскости), будут в этой сумме давать разный знак:
— точка лежит «выше» гиперплоскости
— точка лежит «ниже» гиперплоскости
Это очень важное наблюдение, поэтому предлагаю его перепроверить простым кодом на Python:

Нужно понимать, что «выше» и «ниже» здесь — понятия условные. Это специально отражено в примере — зелёные точки оказываются визуально ниже. С геометрической точки зрения направление «выше» для данной конкретной линии определяется вектором нормали. Куда смотрит нормаль, там и верх:

Т.о. знак линейной комбинации позволяет отнести точку к верхнему или нижнему подпространству.
А значение? Значение (по модулю) определяет удалённость точки от плоскости:
Т.е. чем дальше от плоскости находится точка, тем больше будет значение линейной комбинации для неё. Если зафиксировать значение линейной комбинации, получим точки, лежащие на прямой, параллельной исходной.
Опять же, наблюдение важное, поэтому перепроверяем:
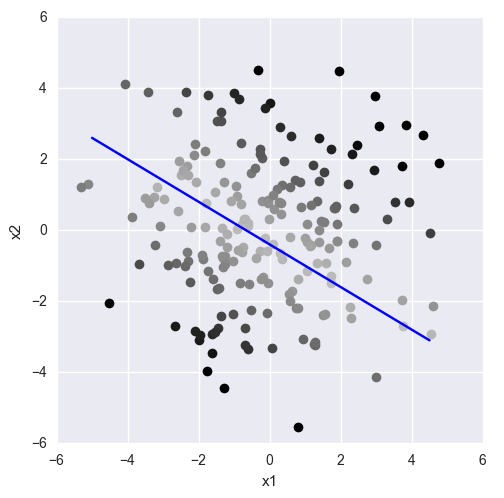
Всё сходится.
С точки зрения бинарной классификации последнее утверждение можно переформулировать следующим образом. Чем удалённее точка от гиперплоскости, являющейся границей решений (decision boundary), тем увереннее мы в том, что наш образец (sample) определяемый этой точкой попадает в тот или иной класс.
Близко и далеко — понятия сугубо субъективные. А при классификации отвечать нам нужно чётко — либо деталь годится для строительства ракеты для полёта на Марс, либо это брак. Либо человек кликнет по рекламе, либо нет. Возможно ответить с долей уверенности — дать вероятность позитивного (true) исхода.
Для этого к линейной комбинации можно применить функцию активации (в терминологии нейросетей).
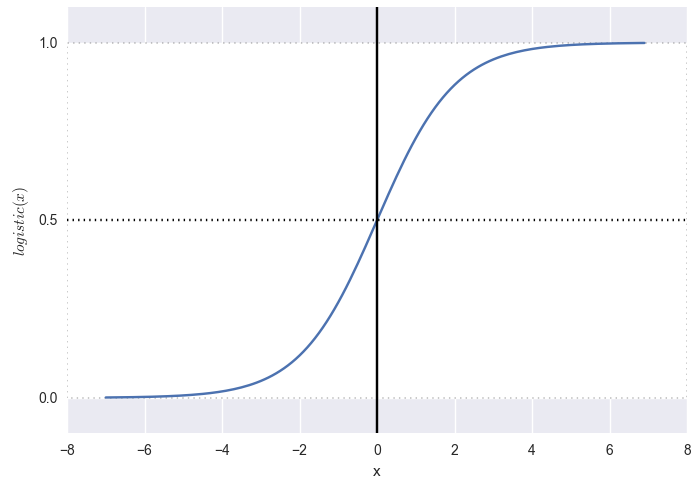
Если применить логистическую функцию (график смотри ниже):
получаем на выходе вероятности и такую картинку:

Красные — точно нет (false, точно брак, точно не кликнет). Зелёные — точно да (true, точно годится, точно кликнет). Всё, что в определённом диапазоне близости от гиперплоскости (граница решений) получает некоторую вероятность. На самой прямой вероятность ровно 0.5.
P.S. «Точно» здесь определяется как меньше 0.001 или больше 0.999. Сама логистическая функция стремится к нулю на минус бесконечности и к единице на плюс бесконечности, но никогда этих значений не принимает.
Казалось бы понятно — мы в пространстве данных (data space), в котором лежат образцы . И ищем оптимальное разделение плоскостью, определяемой вектором .
для зелёных точек
для красных точек
Но в нашей задаче бинарной классификации образцы зафиксированы, а веса меняются. Соответственно мы можем всё переиграть, перейдя в пространство весов (weight space):
Образцы из тренировочного набора в этом случае задают гиперплоскостей и наша задача в том, чтобы найти такую точку , которая бы лежала с нужной стороны от каждой плоскости. Если исходный датасет является линейно-разделимым, то такая точка найдётся.

При обучении модели удобнее рассуждать в пространстве весов, т.к. обновляются веса, а вектора-образцы из тренировочного набора задают нормали к гиперплоскостям. Например:

Предположим, что образцу соответствует зелёный класс, соответствующий неравенству:
Т.к. на иллюстрации вектор смотрит против нормали , то значение линейной комбинации будет отрицательным — следовательно мы имеем ошибку классификации.
Соответственно необходимо обновить вектор в сторону, указываемую нормалью:
, где
с некоторой «скоростью» . Тем самым на следующем шаге предсказание будет либо верным, либо менее неверным, т.к. слагаемое , сонаправленное с нормалью, «довернёт» вектор весов в зелёную область.
Надеюсь эта статья позволит вам лучше понять и прочувствовать геометрический смысл линейных комбинаций. Ниже ссылки на материалы, использованные при подготовке статьи и интересные с точки зрения углубления в тему. (Все материалы на английском языке.)
В статье попробуем ответить на этот вопрос с примерами, формулами, а также множеством иллюстраций и кода на Python, чтобы вы могли легко всё воспроизвести и поставить свои собственные эксперименты.
Модельный пример
Чтобы теория не отрывалась от реальных кейсов, возьмём в качестве примера задачу бинарной классификации. Есть датасет: m образцов, каждый образец — n-мерная точка. Для каждого образца мы знаем к какому классу он относится (зелёный или красный). Также известно, что датасет является линейно разделимым, т.е. существует n-мерная гиперплоскость такая, что зелёные точки лежат по одну сторону от неё, а красные — по другую.

К решению задачи поиска такой гиперплоскости можно подходить разными способами, например с помощью логистической регрессии (logistic regression), метода опорных векторов с линейным ядром (linear SVM) или взять простейшую нейросеть:

От прямой линии до гиперплоскости
Рассмотрим подробную математику для прямой. Для общего случая гиперплоскости в n-мерном пространстве будет всё ровно тоже самое, с поправкой на количество компонент в векторах.
Прямая линия на плоскости задаётся тремя числами — :
или:
или:
Первые два коэффициента задают всё семейство прямых линий, проходящих через точку (0, 0). Соотношение между и определяет угол наклона прямой к осям.
Если , получаем линию, идущую под углом 45 градусов () к осям и и делящую первый/третий квадранты пополам.
Ненулевой коэффициент позволяет линии не проходить через ноль. При этом наклон к осям и не меняется. Т.е. задаёт семейство параллельных линий:
Геометрический смысл вектора — это нормаль к прямой :
(Если не учитывать смещение , то — это не более чем скалярное произведение двух векторов. Равенство нулю равносильно их ортогональности. Следовательно, — семейство векторов, ортогональных .)
P.S. Понятно, что таких нормалей бесконечно много, как и троек (w1, w2, b) задающих прямую. Если все три числа умножить на ненулевой коэффициент — прямая останется той же.
В общем случае n-мерного пространства, задаёт n-мерную гиперплоскость.
или:
или:
Геометрический смысл линейной комбинации
Если точка лежит на гиперплоскости, то
А что происходит с этой суммой, если точка не лежит на плоскости?
Гиперплоскость делит гиперпространство на два гиперподпространства. Так вот точки, находящиеся в одном из этих подпространств (условно говоря «выше» гиперплоскости), и точки, находящиеся в другом из этих подпространств (условно говоря «ниже» гиперплоскости), будут в этой сумме давать разный знак:
— точка лежит «выше» гиперплоскости
— точка лежит «ниже» гиперплоскости
Это очень важное наблюдение, поэтому предлагаю его перепроверить простым кодом на Python:
Код примера на Python
# для красоты
# можете закомментировать, если у вас не установлен этот пакет
import seaborn
import matplotlib.pyplot as plt
import numpy as np
# наша линия: w1 * x1 + w2 * x2 + b = 0
def line(x1, x2):
return -3 * x1 - 5 * x2 - 2
# служебная функция в форме x2 = f(x1) (для наглядности)
def line_x1(x1):
return (-3 * x1 - 2) / 5
# генерируем диапазон точек
np.random.seed(0)
x1x2 = np.random.randn(200, 2) * 2
# рисуем точки
for x1, x2 in x1x2:
value = line(x1, x2)
if (value == 0): # синие — на линии
plt.plot(x1, x2, 'ro', color='blue')
elif (value > 0): # зелёные — выше линии
plt.plot(x1, x2, 'ro', color='green')
elif (value < 0): # красные — ниже линии
plt.plot(x1, x2, 'ro', color='red')
# выставляем равное пиксельное разрешение по осям
plt.gca().set_aspect('equal', adjustable='box')
# рисуем саму линию
x1_range = np.arange(-5.0, 5.0, 0.5)
plt.plot(x1_range, line_x1(x1_range), color='blue')
# проставляем названия осей
plt.xlabel('x1')
plt.ylabel('x2')
# на экран!
plt.show()
Нужно понимать, что «выше» и «ниже» здесь — понятия условные. Это специально отражено в примере — зелёные точки оказываются визуально ниже. С геометрической точки зрения направление «выше» для данной конкретной линии определяется вектором нормали. Куда смотрит нормаль, там и верх:
Т.о. знак линейной комбинации позволяет отнести точку к верхнему или нижнему подпространству.
А значение? Значение (по модулю) определяет удалённость точки от плоскости:
Т.е. чем дальше от плоскости находится точка, тем больше будет значение линейной комбинации для неё. Если зафиксировать значение линейной комбинации, получим точки, лежащие на прямой, параллельной исходной.
Опять же, наблюдение важное, поэтому перепроверяем:
Код примера на Python
# для красоты
# для красоты
# можете закомментировать, если у вас не установлен этот пакет
import seaborn
import matplotlib.pyplot as plt
import numpy as np
# наша линия: w1 * x1 + w2 * x2 + b = 0
def line(x1, x2):
return -3 * x1 - 5 * x2 - 2
# служебная функция в форме x2 = f(x1) (для наглядности)
def line_x1(x1):
return (-3 * x1 - 2) / 5
# генерируем диапазон точек
np.random.seed(0)
x1x2 = np.random.randn(200, 2) * 2
# рисуем точки
for x1, x2 in x1x2:
value = line(x1, x2)
# цвет тем тенее, чем меньше значение — поэтому минус
# коэффициенты — чтобы попасть в диапазон [0, 0.75]
# чёрный (0) — самые удалённые точки, светло-серый (0.75) — самые близкие
color = str(max(0, 0.75 - np.abs(value) / 30))
plt.plot(x1, x2, 'ro', color=color)
# выставляем равное пиксельное разрешение по осям
plt.gca().set_aspect('equal', adjustable='box')
# рисуем саму линию
x1_range = np.arange(-5.0, 5.0, 0.5)
plt.plot(x1_range, line_x1(x1_range), color='blue')
# проставляем названия осей
plt.xlabel('x1')
plt.ylabel('x2')
# на экран!
plt.show()
Всё сходится.
Выводы
- Линейная комбинация позволяет разделить n-мерное пространство гиперплоскостью.
- Точки по разные стороны гиперплоскости будут иметь разный знак линейной комбинации .
- Чем точка удалённее от гиперплоскости, тем абсолютное значение линейной комбинации будет больше.
С точки зрения бинарной классификации последнее утверждение можно переформулировать следующим образом. Чем удалённее точка от гиперплоскости, являющейся границей решений (decision boundary), тем увереннее мы в том, что наш образец (sample) определяемый этой точкой попадает в тот или иной класс.
Близко и далеко: это как?
Близко и далеко — понятия сугубо субъективные. А при классификации отвечать нам нужно чётко — либо деталь годится для строительства ракеты для полёта на Марс, либо это брак. Либо человек кликнет по рекламе, либо нет. Возможно ответить с долей уверенности — дать вероятность позитивного (true) исхода.
Для этого к линейной комбинации можно применить функцию активации (в терминологии нейросетей).
Если применить логистическую функцию (график смотри ниже):
получаем на выходе вероятности и такую картинку:
Код примера на Python
# для красоты
# можете закомментировать, если у вас не установлен этот пакет
import seaborn
import matplotlib.pyplot as plt
import numpy as np
# логистическая функция
def logit(x):
return 1 / (1 + np.exp(-x))
# наша линия: w1 * x1 + w2 * x2 + b = 0
def line(x1, x2):
return 3 * x1 + 5 * x2 + 2
# служебная функция в форме x2 = f(x1) (для наглядности)
def line_x1(x1):
return (-3 * x1 - 2) / 5
# генерируем диапазон точек
np.random.seed(0)
xy = np.random.randn(200, 2) * 2
# рисуем точки
for x1, x2 in x1x2:
# деление добавляется для наглядности — эдакая ручная нормализация
value = logit(line(x1, x2) / 2)
if (value < 0.001):
color = 'red'
elif (value > 0.999):
color = 'green'
else:
color = str(0.75 - value * 0.5)
plt.plot(x1, x2, 'ro', color=color)
# выставляем равное пиксельное разрешение по осям
plt.gca().set_aspect('equal', adjustable='box')
# рисуем саму линию
x1_range = np.arange(-5.0, 5.0, 0.5)
plt.plot(x1_range, line_x1(x1_range), color='blue')
# проставляем названия осей
plt.xlabel('x1')
plt.ylabel('x2')
# на экран!
plt.show()Красные — точно нет (false, точно брак, точно не кликнет). Зелёные — точно да (true, точно годится, точно кликнет). Всё, что в определённом диапазоне близости от гиперплоскости (граница решений) получает некоторую вероятность. На самой прямой вероятность ровно 0.5.
P.S. «Точно» здесь определяется как меньше 0.001 или больше 0.999. Сама логистическая функция стремится к нулю на минус бесконечности и к единице на плюс бесконечности, но никогда этих значений не принимает.
В каком мы пространстве? (полезное умозрительное упражнение)
Казалось бы понятно — мы в пространстве данных (data space), в котором лежат образцы . И ищем оптимальное разделение плоскостью, определяемой вектором .
для зелёных точек
для красных точек
Но в нашей задаче бинарной классификации образцы зафиксированы, а веса меняются. Соответственно мы можем всё переиграть, перейдя в пространство весов (weight space):
Образцы из тренировочного набора в этом случае задают гиперплоскостей и наша задача в том, чтобы найти такую точку , которая бы лежала с нужной стороны от каждой плоскости. Если исходный датасет является линейно-разделимым, то такая точка найдётся.
Код примера на Python
# для красоты
# можете закомментировать, если у вас не установлен этот пакет
import seaborn
import matplotlib.pyplot as plt
import numpy as np
# образец 1
def line1(w1, w2):
return -3 * w1 - 5 * w2 - 8
# служебная функция в форме w2 = f1(w1) (для наглядности)
def line1_w1(w1):
return (-3 * w1 - 8) / 5
# образец 2
def line2(w1, w2):
return 2 * w1 - 3 * w2 + 4
# служебная функция в форме w2 = f2(w1) (для наглядности)
def line2_w1(w1):
return (2 * w1 + 4) / 3
# образец 3
def line3(w1, w2):
return 1.2 * w1 - 3 * w2 + 4
# служебная функция в форме w2 = f2(w1) (для наглядности)
def line3_w1(w1):
return (1.2 * w1 + 4) / 3
# образец 4
def line4(w1, w2):
return -5 * w1 - 5 * w2 - 8
# служебная функция в форме w2 = f2(w1) (для наглядности)
def line4_w1(w1):
return (-5 * w1 - 8) / 5
# генерируем диапазон точек
w1_range = np.arange(-5.0, 5.0, 0.5)
w2_range = np.arange(-5.0, 5.0, 0.5)
# рисуем веса (w1, w2), лежащие по нужные стороны от образцов
for w1 in w1_range:
for w2 in w2_range:
value1 = line1(w1, w2)
value2 = line2(w1, w2)
value3 = line3(w1, w2)
value4 = line4(w1, w2)
if (value1 < 0 and value2 > 0 and value3 > 0 and value4 < 0):
color = 'green'
else:
color = 'pink'
plt.plot(w1, w2, 'ro', color=color)
# выставляем равное пиксельное разрешение по осям
plt.gca().set_aspect('equal', adjustable='box')
# рисуем саму линию (гиперплоскость) для образца 1
plt.plot(w1_range, line1_w1(w1_range), color='blue')
# для образца 2
plt.plot(w1_range, line2_w1(w1_range), color='blue')
# для образца 3
plt.plot(w1_range, line3_w1(w1_range), color='blue')
# для образца 4
plt.plot(w1_range, line4_w1(w1_range), color='blue')
# рисуем только эту область — остальное не интересно
plt.axis([-7, 7, -7, 7])
# проставляем названия осей
plt.xlabel('w1')
plt.ylabel('w2')
# на экран!
plt.show()При обучении модели удобнее рассуждать в пространстве весов, т.к. обновляются веса, а вектора-образцы из тренировочного набора задают нормали к гиперплоскостям. Например:
Предположим, что образцу соответствует зелёный класс, соответствующий неравенству:
Т.к. на иллюстрации вектор смотрит против нормали , то значение линейной комбинации будет отрицательным — следовательно мы имеем ошибку классификации.
Соответственно необходимо обновить вектор в сторону, указываемую нормалью:
, где
с некоторой «скоростью» . Тем самым на следующем шаге предсказание будет либо верным, либо менее неверным, т.к. слагаемое , сонаправленное с нормалью, «довернёт» вектор весов в зелёную область.
Итоги
Надеюсь эта статья позволит вам лучше понять и прочувствовать геометрический смысл линейных комбинаций. Ниже ссылки на материалы, использованные при подготовке статьи и интересные с точки зрения углубления в тему. (Все материалы на английском языке.)
- Geoffrey Hinton. An overview of the main types of neural network architecture
Подробнее про обучение персептрона с переходом в пространство весов от гуру нейронных сетей Джеффри Хинтона.
- Supervised Learning / Support Vector Machines
Про решение задач бинарной классификации методом опорных векторов и как с точки зрения этого алгоритма выбрать оптимальную разделяющую плоскость.
- Hyperplane based сlassification: Perceptron and (Intro to) Support Vector Machines
Опять про персептроны, вскользь про метод опорных векторов. Детально рассматривается вопрос обучения и корректировки весов.
- Polyhedra and Linear Programming. Polyhedra, Polytopes, and Cones
Линейная алгебра линейных комбинаций (теория) с множеством иллюстративных примеров.
Поделиться с друзьями
Комментарии (4)

Dark_Daiver
24.03.2017 18:30Вероятно самое иллюстрированное объяснение линейной комбинации что я видел в своей жизни

yorko
24.03.2017 19:43А цель статьи была пояснить только смысл линейной комбинации?
А то столько слов про логистическую регрессию, SVM, нейронные сети, простигосподи. И так быстро все кончилось.
Пс. Можно уточнить, что последнее, к чему пришли — это простой перцептрон, кирпичик, заложенный в фундамент нейросетей.


ServPonomarev
Про сигмоиду в разделе 'близко-далеко' не согласен.
Возьмём нашу регрессию, возьмём обучающую и тестовую выборки. Найдём максимальное значение ложнопозитивного срабатывания и минимальное значение ложнонегативного. Те точки, которые лежат выше и ниже этих границ — можно считать точками высокой уверенности результатов. Те точки, что располагаются между этими двумя границами — это и есть рабочая область классификатора. Если построить графики полноты-точности для этой области, то мы увидим классический крест. Место пересечения графиков точности и полноты можно принять за 50%, нижнюю границу за 0%, верхнюю за 100% (да, обычно получается несимметрично). Тогда ответом классификатора будет человеко-интуитивно понимаемая оценка в виде процентов.
Если хотите использовать сигмод — тоже можно, но границы срабатывания («уверенности») определять тогда по количеству сигм. 2 сигмы для бизнес задач — уже выше крыши.
kdenisk
Согласен. Правда вы говорите про трактовку результатов работы классификатора, а пример демонстрировал как расстояния из R нелинейно ужимаются (squashing) в интервал вероятностей (0, 1).
Границы уверенности в данном случае фиксированы и выбраны просто для целей иллюстрации.