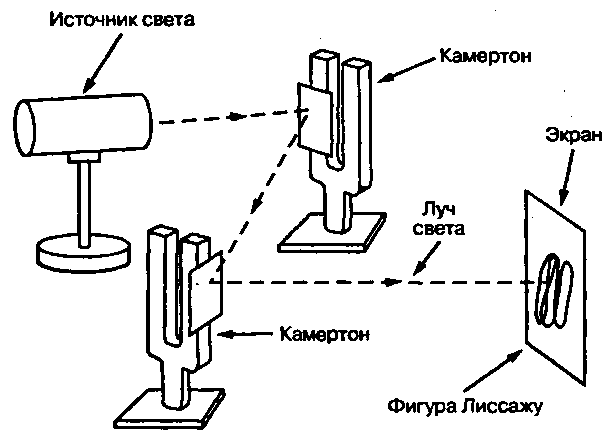
Картинки из сети, качество желает лучшего, но они достаточно точно отражают суть опыта по визуализации фигур. Зри в корень – основа мудрости поколений.
Немного истории
Ещё в школе на уроках физики я вглядывался в осциллограф, на экране которого, сменяя друг друга, появлялись разные фигуры: сначала простые – линия, парабола, круг, эллипс, потом фигуры становились всё более насыщенные непрерывными волнообразными линиями, напоминающие мне кружева. Автором этого кружевного дива был Жюль Антуан Лиссажу французский физик, член — корреспондент Парижской АН (1879) [1]. Сами фигуры — это замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях [2]. Думаю, что в те далёкие от современности годы основной заслугой Жюля, кроме конечно накопленных опытом знаний математики и физики, была простая механическая визуализация этих фигур подручными средствами. Захотелось конструировать подобно Жулю максимально просто и наглядно, реализовать его идеи применительно к современной задаче линейных измерений. Но сделать это путём математического моделирования с графической визуализацией его результатов на Python. Но сначала рассмотрим классический вариант [3] построения фигур.
Какими должны быть фигуры Лиссажу
Для этого воспользуемся системой уравнений, описывающих фигуры:
x(t), y(t) в общем случае зависящие от времени гармонические колебания вдоль взаимно перпендикулярных плоскостей, частоты b, a и начальная фаза d. Для анализа фигур в вычислениях принимают постоянным модуль разности частот |b — a| = 1. Будем рассматривать отношение круговых частот b / a и начальную фазу d. Имеем для линии A = B d = 0, окружности
, и параболы 
. Основные отношения частот, удовлетворяющие условию, занесём во вложенный список m=[[0],[2,2],[2,1],[1,2],[3,2],[3,4],[5,4],[5,6],[9,8]].Код для построения графиков каждой из фигур на отдельных графиках
#!/usr/bin/env python
#coding=utf8
import numpy as np
from numpy import sin,pi
import matplotlib.pyplot as plt
m=[[0],[2,2],[2,1],[1,2],[3,2],[3,4],[5,4],[5,6],[9,8]]# отношение круговых частот
for i in m:
if i[0]==0:
a=1
x=[sin(a*t) for t in np.arange(0.,2*pi,0.01)]
y=[sin(a*t) for t in np.arange(0.,2*pi,0.01)]
plt.plot(x, y, 'r')# график для линии
plt.grid(True)
plt.show()
else:
a=i[0]
b=i[1]
d=0.5*pi
x=[sin(a*t+d) for t in np.arange(0.,2*pi,0.01)]
y=[sin(b*t) for t in np.arange(0.,2*pi,0.01)]
plt.plot(x, y, 'r') # график для различных отношений a/b
#круговых частот
plt.grid (True)
plt.show()
Результат не привожу, отдельные фигуры не впечатляют. Хочу коллаж из «кружев».
Код программы для построения на одной форме графиков для четырёх фигур при m= [3,4], [5,4],[5,6],[9,8]]
#!/usr/bin/env python
#coding=utf8
import numpy as np
from numpy import sin,pi
import matplotlib.pyplot as plt
m=[[3,4],[5,4],[5,6],[9,8]] # отношение круговых частот
plt.figure(1)
for i in m:
a=i[0]
b=i[1]
d=0.5*pi
x=[sin(a*t+d) for t in np.arange(0.,2*pi,0.01)]
y=[sin(b*t) for t in np.arange(0.,2*pi,0.01)]
if m.index(i)==0:
plt.subplot(221)
plt.plot(x, y, 'k') # график для различных отношений a/b круговых частот
plt.grid(True)
elif m.index(i)==1:
plt.subplot(222)
plt.plot(x, y, 'g')
plt.grid(True)
elif m.index(i)==2:
plt.subplot(223)
plt.plot(x, y, 'b')
plt.grid(True)
else:
plt.subplot(224)
plt.plot(x, y, 'r')
plt.grid(True )
plt.show()
И вот они «кружева».
Что нельзя отнести к фигурам Лиссажу по определению о их замкнутости
Зачем нам |b — a| = 1, “за флажки!” попробуем например так m=[[1,3],[1,5],[1,7],[1,9]]
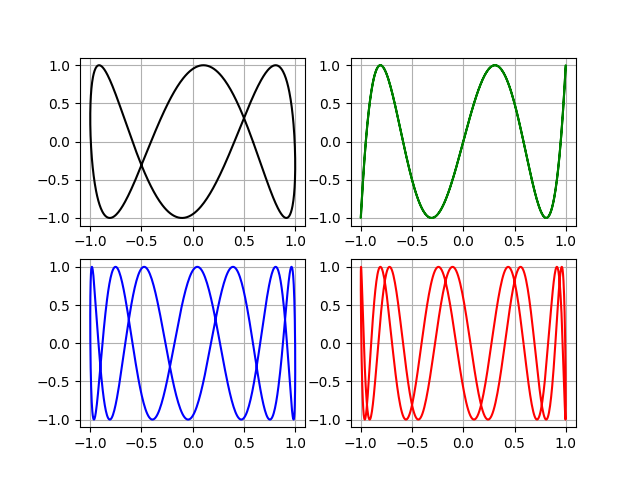
На втором графике при m=0,2 получена незамкнутая траектория, которая по определению не является фигурой Лbссажу.
В поисках механических аналогов
Поищем аналогии фигур в измерительной технике и вот вибрационный уровнемер с резонатором в виде эллиптической трубки [4].
Упруго закреплённая трубка эллиптического сечения с помощью систем возбуждения 5,6,7 совершает автоколебания в одной плоскости, а с помощью систем 8, 9, 10 в другой плоскости перпендикулярной первой. Трубка колеблется в двух взаимно перпендикулярных плоскостях с разными частотами близкими к собственным. Масса трубки зависит от уровня заполняющей её жидкости. С изменением массы меняются и частоты колебаний трубки, которые и являются выходными сигналами уровнемера. Частоты несут дополнительную информацию о мультипликативных и аддитивных дополнительных погрешностях, компенсируемых при обработке частот микропроцессором 11.
Условия адекватного моделирования
Для более-менее корректной привязки фигур Лиссажу к работе упомянутого уровнемера, следует учесть следующие обстоятельства. Во-первых, закреплённая одним концом трубка эллиптического сечения — это колебательная система с распределёнными параметрами, что сильно усложняет анализ её колебаний. Во-вторых, отношение частот колебаний трубки не может изменяться произвольно, оно зависит от эллипсности сечения и допустимых зазоров в системе возбуждения колебаний. Для отношения частот можно получить простое соотношение.
К чему принадлежат переменные, a, b, a0, b0 ясно из рисунка и кроме того формула для циклической частоты осциллятора известна из школьного курса физики. Для «реализации на Python в последнее отношение введём толщину стенки и показатель эллипсности внутреннего сечения трубки, тогда вместо четырёх переменных получим три.
Код программы для определения. допустимого изменения отношения частот
#!/usr/bin/env python
#coding=utf8
import numpy as np
from numpy import sqrt
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
d=0.5
a=9
x=[w for w in np.linspace(0.8,0.95,15)]
y=[sqrt(x**-2*((1+d/a)**3*(1+d/(x*a))-1)/((1+d/a)*(1+d/(x*a))**3-1)) for x in np.linspace(0.8,0.95,15)]
plt.plot(x, y, 'r', label='Толщина стенки трубки в мм. -- %s' %str(d))
d=0.7
y=[sqrt(x**-2*((1+d/a)**3*(1+d/(x*a))-1)/((1+d/a)*(1+d/(x*a))**3-1)) for x in np.linspace(0.8,0.95,15)]
plt.plot(x, y, 'b',label='Толщина стенки трубки в мм.-- %s' %str(d))
d=1.0
y=[sqrt(x**-2*((1+d/a)**3*(1+d/(x*a))-1)/((1+d/a)*(1+d/(x*a))**3-1)) for x in np.linspace(0.8,0.95,15)]
plt.plot(x, y, 'g', label='Толщина стенки трубки в мм.-- %s' %str(d))
plt.ylabel('Отношение частот колебаний эллиптической трубки')
plt.xlabel('Отношение длин малой и большой полуосей')
plt.title('Определение допустимого диапазона для отношения частот')
plt.legend(loc='best')
plt.grid(True)
plt.show()
В результате работы программы получим график.
График построен для малой внутренней полуоси в 9 мм. Для конструктивно допустимого отношения малой к большой полуоси сечения в диапазоне от 0.8 до 0.95. Это основной фактор влияния на отношение частот, которое изменяется от 1.18 до 1.04. Толщина стенки влияет незначительно. Теперь у нас есть диапазон отношений и ним можно воспользоваться для дальнейшего моделирования.
Формы колебаний вертикальной оси трубки
Что касается распределённых механических параметров консольной трубки, то они при помощи равенства собственных частот и импеданса могут быть приведены к сосредоточенной массе жёсткости и демпфированию. Кроме того, для определения форм изгибных колебаний консольной трубки можно получить выражение для распределённых параметров. Уравнение для форм – балочные функции имеет вид:
где
— корни уравнения:
Следует отметить что, не смотря на большое количество публикаций о формах и частотах колебаний консольного стержня, балки или трубки уравнения (4) нигде не приводяться, только рисунки без координат. Поэтому уравнение (4), я вывел через условия на концах и балочные функции, проверил по корням (5) и расположению узлов. Однако это тривиальное уравнение, о котором просто забыли.
Код программы для численного определения корней уравнения 1.1 и построения трёх форм изгибных колебаний оси трубки
1.1 —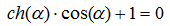 
#!/usr/bin/env python
#coding=utf8
from scipy.optimize import *
import numpy as np
from numpy import pi,cos,cosh,sin,sinh
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
d=[]
for i in range(0,4):
x=brentq(lambda x:cosh(x)*cos(x)+1,0+pi*i,pi+pi*i)
p=round(x,3)
if p not in d:
d.append(p)
x=[w for w in np.linspace(0,1,100)]
k=d[0]
z=[sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x) )for x in np.linspace(0,1,100)]
plt.plot(z, x, 'g', label='Первая форма для корня - %s' %str(k))
k=d[1]
z=[sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x)) for x in np.linspace(0,1,100)]
plt.plot(z, x, 'b', label='Вторая форма для корня - %s' %str(k))
k=d[2]
z=[sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x)) for x in np.linspace(0,1,100)]
plt.plot(z, x, 'r', label='Третья форма для корня - %s' %str(k))
plt.title('Первые три формы изгибных колебаний осевой линии трубки')
plt.xlabel(' Координата вдоль оси OX ')
plt.ylabel(' Координата положения осевой линии трубки вдоль оси OZ ')
plt.legend(loc='best')
plt.grid(True)
plt.show()
В результате работы программы получим график построенный с учётом вертикального положения трубки.
На графике координата осевой линии приведена к длине трубки, а амплитуда нормирована. Положение узлов колебаний трубки относительно места её крепления в точности соответствует теории колебаний.
По каким траекториям движется конец трубки
Последнее препятствие — сложность получения осмысленного численного решения дифференциальных уравнений колебаний, при условии варьирования несколькими параметрами одновременно. Тут на помощь пришли две мои статьи о колебательном звене на Python [5,6], в которых приведена методика получения точных символьных решений дифференциальных уравнений.
Запишем два условно независимых уравнения для колебаний трубки в плоскости OX и OY с разными частотами a и b отношение между которыми выбрано из ранее установленного диапазона. Остальные параметры выбраны во правильной взаимосвязи, но произвольно для лучшей демонстрации результата.
Здесь введены следующие обозначения (для упрощения без индексов).
- приведенная амплитуда силы, 
- коэффициент затухания, 
- собственная частота колебаний системы, m - сосредоточенная масса одинаковая для обоих уравнений, 
- сосредоточенные коэффициенты демпфирования, разные из-за разных амплитуд, а следовательно разных зазорах в системах возбуждения колебаний, 
- разные жёсткости из-за эллиптичности сечения трубки. Код программы для решения каждого дифференциального уравнения системы (6), с последующем сложением для получения траектории движения конца трубки.
import numpy as np
from sympy import *
from IPython.display import *
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
def solution(w,v,i,n1,n2,B,f,N):
t=Symbol('t')
var('t C1 C2')
u = Function("u")(t)
de = Eq(u.diff(t, t) +2*B*u.diff(t) +w**2* u, f*sin(w*t+v))
des = dsolve(de,u)
eq1=des.rhs.subs(t,0)
eq2=des.rhs.diff(t).subs(t,0)
seq=solve([eq1,eq2],C1,C2)
rez=des.rhs.subs([(C1,seq[C1]),(C2,seq[C2])])
g= lambdify(t, rez, "numpy")
t= np.linspace(n1,n2,N)
plt.figure(1)
if i==1:
plt.subplot(221)
plt.plot(t,g(t),color='b', linewidth=3,label='x=%s*sin(%s*t+%s)' %(str(f),str(w),str(v)))
plt.legend(loc='best')
plt.grid(True)
else:
plt.subplot(222)
plt.plot(t,g(t),color='g', linewidth=3,label='y=%s*sin(%s*t+%s)' %(str(f),str(w),str(v)))
plt.legend(loc='best')
plt.plot(t,g(t),color='r', linewidth=3)
plt.grid(True)
return g(t)
N=1000#Число точек оцифровки временного интервала
B=0.2#Установка демпфирования
f=1#Установка амплитуды
n1=0#Нижняя граница временной развертки
n2=20#Верхняя граница временной развёртки
w1=5.0#Частота колебаний трубки вдоль оси ОХ
w2=10.0#Частота колебаний трубки вдоль оси ОУ
v1=0#Начальная фаза при колебании вдоль оси ОХ
v2=0#Начальная фаза при колебании вдоль оси ОУ
g1=solution(w1,v1,1,n1,n2,B,f,N)
g2=solution(w2,v2,2,n1,n2,B,f,N)
plt.subplot(223)
plt.plot(g1,g2,color='b', linewidth=3,label='w1/w2=%s'%str(w1/w2))
plt.legend(loc='best')
plt.grid(True)
plt.subplot(224)
x=[w for w in np.linspace(0,1,100)]
k=1.875
z=[sin(k*x)-sinh(k*x)+((cosh(k) -cos(k))/(sin(k)-sinh(k)))*(cos(k*x)-cosh(k *x) )for x in np.linspace(0,1,100)]
plt.plot(z, x, 'g',label='Форма -%s'%str(k))
plt.legend(loc='best')
plt.grid(True)
plt.show()
Программа позволяет менять все параметры модели, например, для:
N=1000, B=0.2, f=1, n1=0, n2=20, w1=5.0, w2=10.0, v1=0, v2=0
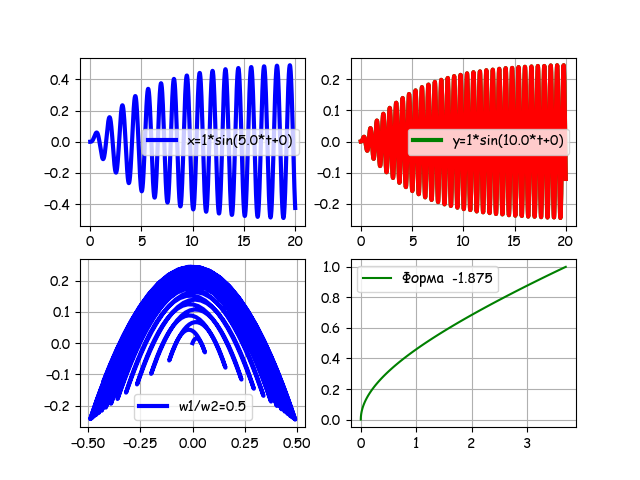
Для отношения частот 0.5 переходной процесс множит фигуры. Поставим “ворота” времени n15=0, n2=20, получим.
Снимем” ворота” и введём начальную фазу v2=-pi/2, получим:
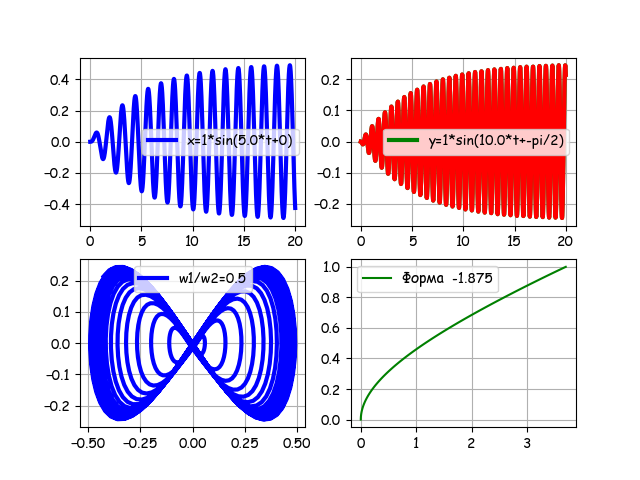
С учётом изложенного выше, графики комментарий не требую.
Для интриги
Если эта статья найдёт своих читателей или читатели её найдут, не устрашившись теней прошлого, то я опубликую трёхмерные анимационные графики сложных пространственных колебаний трубки при изменении в ней уровня заполняющей жидкости.
Вместо выводов
Изобретение Жюля Антуана Лиссажу продолжает свой путь во времени, но уже и на Python. Надеюсь, что представленная интерпретация, конечно далёкая от совершенства, позволит продолжить знакомство с работами гениального математика Лиссажу.
Ссылки
Поделиться с друзьями
Комментарии (2)
red_andr
05.05.2017 19:16Занятно, спасибо. Фигуры Лиссажу были моей первой серьёзной программой, ещё на Бейсике.
hardtop
Отлично. Как раз ребенку показываю всякие несложные штуки на питоне. Спасибо!