
Нет более полезного инструмента для исследования, чем подтверждённая практикой теория.
Зачем нужна информационная теория измерений
В предыдущей публикации [1] мы рассмотрели подбор закона распределения случайной величины по данным статистической выборки и только упомянули об информационном подходе к анализу погрешности измерений. Поэтому продолжим обсуждение этой актуальной темы.
Преимущество информационного подхода к анализу результатов измерений состоит в том, что размер энтропийного интервала неопределенности можно найти для любого закона распределения случайной погрешности. Это исключает «недоразумения» при произвольном выборе значений доверительной вероятности.
Кроме того, по совокупности вероятностных и информационных характеристикам выборки можно более точно определить характер распределения случайной погрешности. Это объясняется обширной базой численных значений таких параметров, как энтропийный коэффициент иконтрэксцесс для различных законов распределения и их суперпозиций.
О сути информационного и вероятностного анализа
Здесь ключевым словом является слово неопределённость. Измерение рассматривается как процесс, в результате которого уменьшается исходная неопределённость в сведениях об измеряемой величине — x. Количественной мерой неопределённости является энтропия — H(x). Чаще мы сталкиваемся с дискретными значениями случайной величины x1, x2…xn, что обусловлено широким распространением средств вычислительной техники. Для таких величин запишем только одну формулу, которая многое объясняет.
Где p_i- вероятность того, что случайная величина х приняла значение x_i. Поскольку 0?p_i?1, а при этом lg?p_i<0, то для получения H(x)?0 перед суммой в формуле стоит знак минус.
Энтропия измеряется в единицах измерения информации. Единицы информации по приведенной формуле зависят от основания логарифма. Для десятичного логарифма это дит. Для натурального логарифма – нит. По понятным причинам наиболее часто используются двоичные логарифмы, при которых з\энтропия измеряется в битах.
В процессе измерения исходная неопределённость величины х уменьшается, поскольку наше знание о величине х возрастает. Однако и после измерения остаётся остаточная неопределённость H(?), связанная с погрешностью измерений ?.
Остаточную энтропию H(?)можно определить по приведенной формуле, подставив вместо x погрешность ? и, опуская промежуточные выкладки, получить энтропийное значение погрешности ? для любого закона распределения.
Как получить энтропийное значение погрешности по результатам измерений
Для этого сначала последовательность дискретных значений случайной величины погрешности нужно разбить на интервалы с последующим подсчётом частот попадания этих значений в каждый интервал. В пределах интервала вероятность появления этих значений погрешности принимают постоянной равной, равной отношению частоты попадания в данный интервал к количеству проведенных измерений.
Другими словами, нужно воспроизвести часть процедуры, которую выполняет функция построения диаграммы hist () из библиотеки matplotlib. Продемонстрируем это на следующей простой процедуре, сравнивая полученную диаграмму с диаграммой, полученной с помощью hist ().
Программа для сравнения методов обработки данных
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import uniform
def diagram(a):
a.sort()# сортировка списка
n=len(a)# число элементов в списке
m= int(10+np.sqrt(n))# количество интервалов разбиения
d=(max(a)-min(a))/m# длина интервалов
x=[];y=[]
for i in np.arange(0,m+1,1):
x.append(min(a)+d*i)#добавление границ интервалов в список х
k=0
for j in a:
if min(a)+d*i <=j<min(a)+d*(i+1):
k=k+1
y.append(k)# добавление частот попадания в интервал в список у
plt.title("Полученная диаграмма")
plt.bar(x,y, d)
plt.grid(True)
plt.show()
plt.title("Диаграмма созданная функцией hist()")
plt.hist(a,m)
plt.grid(True)
plt.show()
a=uniform.rvs(size=500) #тестовая выборка с равномерным распределением
diagram(a)
Сравним полученные диаграммы.


Диаграммы почти идентичны.Большее на единицу чем в функции hist() число интервалов разбиения только улучшит результат анализа. Поэтому можно приступать ко второму этапу получения энтропийного значения погрешности, для этого воспользуемся соотношением, приведенном в [2] и полученным из соотношения (2).
В приведенном выше листинге в списке х хранятся значения границ интервалов, а в списке у — частоты попадания значений погрешностей в эти интервалы. Перепишем (3) в строку листинга Python.
h=0.5*d*n*10** (-sum ([w*np.log10 (w) for w in y if w! =0])/n)
Для окончательного решения нашей задачи нам понадобятся ещё два значения энтропийного коэффициента k и контрэксцесса psi, возьмём их из [2], но запишем для Python.
k=h/np.std (a)
mu4=sum ([(w-np.mean (a))**4 for w in a])/n
mu4=sum ([(w-np.mean (a))**4 for w in a])/n
Остаётся добавить в листинг приведенные четыре строки, но для анализа окончательного результата следует рассмотреть ещё один важный вопрос.
Как можно использовать энтропийный коэффициент и контрэксцесс для классификации законов распределения погрешности
Согласно теории вероятности, форма закона распределения характеризуется относительным четвёртым моментом или контрэксцессом. В теории информации форма закона распределения определяется значением энтропийного коэффициента. Учитывая сказанное, на плоскость psi, k разместим точки, соответствующие заданным законам распределения. Но вначале получим значения psi, k и диаграммы для пяти наиболее значимых законов распределения погрешностей.
Программа для получения числовых значений psi, k и построения диаграмм
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import logistic,norm,uniform,erlang,pareto,cauchy
def diagram(a,nr):
a.sort()
n=len(a)
m= int(10+np.sqrt(n))
d=(max(a)-min(a))/m
x=[];y=[]
for i in np.arange(0,m+1,1):
x.append(min(a)+d*i)
k=0
for j in a:
if min(a)+d*i <=j<min(a)+d*(i+1):
k=k+1
y.append(k)
h=0.5*d*n*10**(-sum([w*np.log10(w) for w in y if w!=0])/n)
k=h/np.std (a)
mu4=sum ([(w-np.mean (a))**4 for w in a])/n
psi=(np.std(a))**2/np.sqrt(mu4)
plt.title("%s : k=%s; psi=%s; h=%s."%(nr,str(round(k,3)),str(round(psi,3)),str(round(h,3))))
plt.bar(x,y, d)
plt.grid(True)
plt.show()
nr="Равномерное распределение"
a=uniform.rvs( size=1000)
nr="Логистическое распределение"
a=logistic.rvs( size=1000)
nr="Нормальное распределение"
a=norm.rvs( size=1000)
nr="Распределение Эрланга "
a = erlang.rvs(4,size=1000)
nr="Распределение Парето "
a = pareto.rvs(4,size=1000)
nr="Распределение Коши "
a = cauchy.rvs(size=1000)
diagram(a,nr)




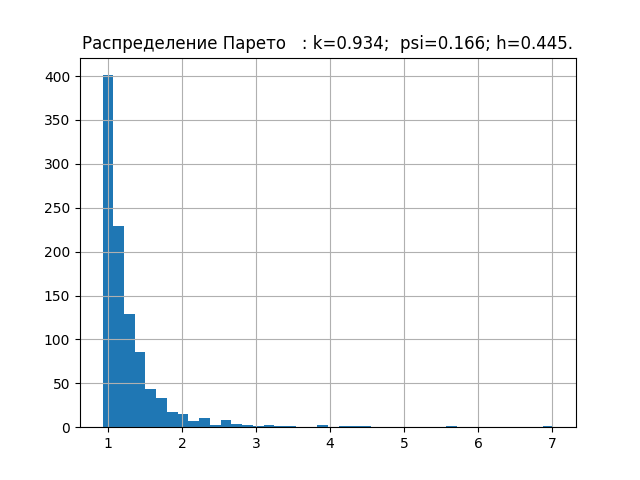

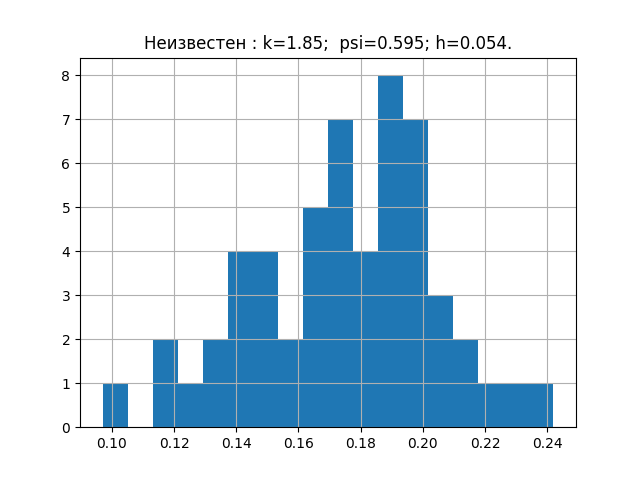
Минимальную базу энтропийных характеристик законов распределения погрешностей мы уже набрали. Теперь проверим теорию на выборке с неизвестным законом распределения, например, такую.
a=[ 0.203, 0.154, 0.172, 0.192, 0.233, 0.181, 0.219, 0.153, 0.168, 0.132, 0.204, 0.165, 0.197, 0.205, 0.143, 0.201, 0.168, 0.147, 0.208, 0.195, 0.153, 0.193, 0.178, 0.162, 0.157, 0.228, 0.219, 0.125, 0.101, 0.211, 0.183, 0.147, 0.145, 0.181, 0.184, 0.139, 0.198, 0.185, 0.202, 0.238, 0.167, 0.204, 0.195, 0.172, 0.196, 0.178, 0.213, 0.175, 0.194, 0.178, 0.135, 0.178, 0.118, 0.186, 0.191]
Если кому интересно, можете сами выбрать любую и проверить. Эта выборка даёт следующую диаграмму с параметрами.
Теперь пришло время перенести полученные параметры на график.
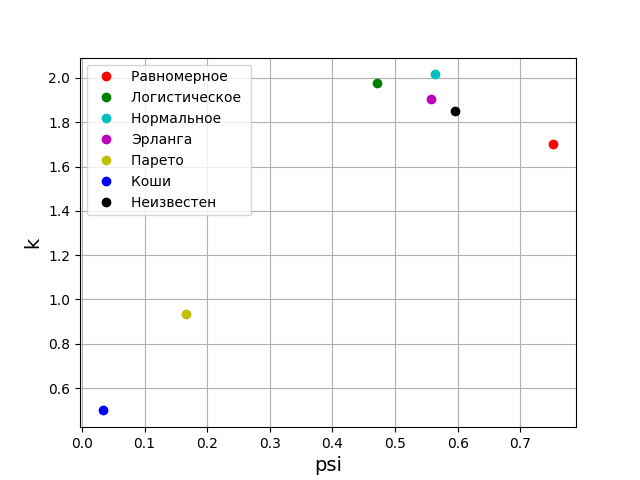
Из приведенного графика видно, что закон распределения для исследуемой выборке ближе всего к закону распределения Эрланга.
Вывод
Надеюсь на то, что рассмотренная в данной публикации реализация на Python элементов информационной теории измерений будет для Вас не безынтересной.
Всем спасибо за внимание!
Ссылки
Поделиться с друзьями


fediq
Диаграммы не идентичны. Обратите внимание на бины в районе
1.0. Видно, что функцияhist()размещает в единице правую границу бина, ваша же функция размещает его центр. Из-за этого на вашем графике появляется лишний бин, а высота предшествующего ему бина оказывается ниже на один пункт.