Мы уже рассмотрели механизм индексирования PostgreSQL и интерфейс методов доступа, а также один из методов доступа — хеш-индекс. Сейчас поговорим о самом традиционном и используемом индексе — B-дереве. Глава получилась большой, запасайтесь терпением.

Btree

Устройство

Индекс btree, он же B-дерево, пригоден для данных, которые можно отсортировать. Иными словами, для типа данных должны быть определены операторы «больше», «больше или равно», «меньше», «меньше или равно» и «равно». Заметьте, что одни и те же данные иногда можно сортировать разными способами, что возвращает нас к концепции семейства операторов.

Как всегда, индексные записи B-дерева упакованы в страницы. В листовых страницах эти записи содержат индексируемые данные (ключи) и ссылки на строки таблицы (TID-ы); во внутренних страницах каждая запись ссылается на дочернюю страницу индекса и содержит минимальное значение ключа в этой странице.

B-деревья обладают несколькими важными свойствами:

• Они сбалансированы, то есть любую листовую страницу отделяет от корня одно и то же число внутренних страниц. Поэтому поиск любого значения занимает одинаковое время.
  
• Они сильно ветвисты, то есть каждая страница (как правило, 8 КБ) содержит сразу много (сотни) TID-ов. За счет этого глубина B-деревьев получается небольшой; на практике до 4–5 для очень больших таблиц.
  
• Данные в индексе упорядочены по неубыванию (как между страницами, так и внутри каждой страницы), а страницы одного уровня связаны между собой двунаправленным списком. Поэтому получить упорядоченный набор данных мы можем, просто проходя по списку в одну или в другую сторону, не возвращаясь каждый раз к корню.
  

Вот схематичный пример индекса по одному полю с целочисленными ключами.



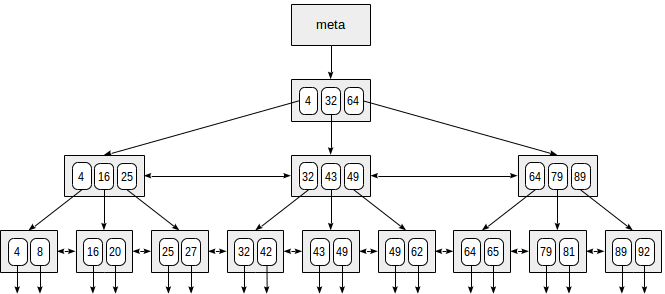
В самом начале файла находится метастраница, которая ссылается на корень индекса. Ниже корня расположены внутренние узлы; самый нижний ряд — листовые страницы. Стрелочки вниз символизируют ссылки из листовых узлов на строки таблицы (TID-ы).

Поиск по равенству

Рассмотрим поиск значения в дереве по условию «индексированное-поле = выражение». Допустим, нас интересует ключ 49.



Поиск начинается с корневого узла, и нам надо определить, в какой из дочерних узлов спускаться. Зная находящиеся в корневом узле ключи (4, 32, 64) мы тем самым понимаем диапазоны значений в дочерних узлах. Поскольку 32 ? 49 < 64, надо спускаться во второй дочерний узел. Дальше та же процедура повторяется рекурсивно до тех пор, пока не будет достигнут листовой узел, из которого уже можно получить необходимые TID-ы.

В реальности эта простая на вид процедура осложняется рядом обстоятельств. Например, индекс может содержать неуникальные ключи и одинаковых значений может оказаться достаточно много, чтобы они не поместились на одну страницу. Продолжая наш пример, кажется, что из внутреннего узла следовало бы спуститься по ссылке, которая ведет от значения 49. Но, как видно на картинке, так мы пропустим один из ключей 49 в предыдущей листовой странице. Поэтому, обнаружив на внутренней странице точное равенство ключа, нам приходится спускаться на одну позицию левее, а затем просматривать индексные записи нижележащего уровня слева направо в поисках интересующего ключа.

(Другая сложность вызвана тем, что во время поиска другие процессы могут изменять данные: дерево может перестраиваться, страницы могут разбиваться на две и т. п. Все алгоритмы построены таким образом, чтобы эти одновременные действия по возможности не мешали друг другу и не требовали лишних блокировок. Но в эти детали мы уже не будем вдаваться.)

Поиск по неравенству

При поиске по условию «индексированное-поле ? выражение» ( или «индексированное-поле ? выражение»), сначала находим в индексе значение по условию равенства «индексированное-поле = выражение» (если оно есть), а затем двигаемся по листовым страницам до конца в нужную сторону.

Рисунок иллюстрирует этот процесс для условия n ? 35:



Аналогично поддерживаются и операторы «больше» и «меньше», надо лишь исключить исходно найденное значение.

Поиск по диапазону

При поиске по диапазону «выражение1 ? индексированное-поле ? выражение2» находим значение по условию «индексированное-поле = выражение1», а затем двигаемся по листовым страницам, пока выполняется условие «индексированное-поле ? выражение2». Или наоборот: начинаем со второго выражения и двигаемся в другую сторону, пока не дойдем до первого.

На рисунке показан процесс для условия 23 ? n ? 64:

Пример

Посмотрим, как выглядят планы запросов на примере. Как обычно, используем демонстрационную базу данных, и на этот раз возьмем таблицу самолетов. В ней всего девять строк и по собственной воле планировщик не будет использовать индекс — ведь вся таблица целиком помещается в одну страницу. Но нам она интересна по причине наглядности.

demo=# select * from aircrafts;
 aircraft_code |        model        | range
---------------+---------------------+-------
 773           | Boeing 777-300      | 11100
 763           | Boeing 767-300      |  7900
 SU9           | Sukhoi SuperJet-100 |  3000
 320           | Airbus A320-200     |  5700
 321           | Airbus A321-200     |  5600
 319           | Airbus A319-100     |  6700
 733           | Boeing 737-300      |  4200
 CN1           | Cessna 208 Caravan  |  1200
 CR2           | Bombardier CRJ-200  |  2700
(9 rows)

demo=# create index on aircrafts(range);
CREATE INDEX

demo=# set enable_seqscan = off;
SET

(Или явно create index on aircrafts using btree(range), но по умолчанию строится именно B-дерево.)

Поиск по равенству:

demo=# explain(costs off) select * from aircrafts where range = 3000;
                    QUERY PLAN                    
---------------------------------------------------
 Index Scan using aircrafts_range_idx on aircrafts
   Index Cond: (range = 3000)
(2 rows)

Поиск по неравенству:

demo=# explain(costs off) select * from aircrafts where range < 3000;
                    QUERY PLAN                    
---------------------------------------------------
 Index Scan using aircrafts_range_idx on aircrafts
   Index Cond: (range < 3000)
(2 rows)

И по диапазону:

demo=# explain(costs off) select * from aircrafts where range between 3000 and 5000;
                     QUERY PLAN                      
-----------------------------------------------------
 Index Scan using aircrafts_range_idx on aircrafts
   Index Cond: ((range >= 3000) AND (range <= 5000))
(2 rows)


Сортировка

Стоит еще раз подчеркнуть, что при любом способе сканирования (индексном, исключительно индексном, по битовой карте) метод доступа btree возвращает упорядоченные данные, что хорошо видно на приведенных выше рисунках.

Поэтому, если на таблице имеется индекс по условию сортировки, оптимизатор будет учитывать обе возможности: обращение к таблице по индексу и автоматическое получение отсортированных данных, либо последовательное чтение таблицы и последующая сортировка результата.

Порядок сортировки

При создании индекса можно явно указывать порядок сортировки. Например, индекс по дальности полета можно было создать и так:

demo=# create index on aircrafts(range desc);

При этом слева в дереве оказались бы большие значения, а справа — меньшие. Зачем это может понадобиться, если по индексированным значениям можно проходить как в одну сторону, так и в другую?

Причина в многоколоночных индексах. Давайте создадим представление, которое будет показывать модели самолетов и условное деление на ближне-, средне- и дальнемагистральные суда:

demo=# create view aircrafts_v as
select model,
       case
           when range < 4000 then 1
           when range < 10000 then 2
           else 3
       end as class
from aircrafts;
CREATE VIEW

demo=# select * from aircrafts_v;
        model        | class
---------------------+-------
 Boeing 777-300      |     3
 Boeing 767-300      |     2
 Sukhoi SuperJet-100 |     1
 Airbus A320-200     |     2
 Airbus A321-200     |     2
 Airbus A319-100     |     2
 Boeing 737-300      |     2
 Cessna 208 Caravan  |     1
 Bombardier CRJ-200  |     1
(9 rows)

И создадим индекс (с использованием выражения):

demo=# create index on aircrafts(
(case when range < 4000 then 1 when range < 10000 then 2 else 3 end), model);
CREATE INDEX

Теперь мы можем использовать этот индекс, чтобы получить данные, отсортированные по обоим столбцам по возрастанию:

demo=# select class, model from aircrafts_v order by class, model;
 class |        model        
-------+---------------------
     1 | Bombardier CRJ-200
     1 | Cessna 208 Caravan
     1 | Sukhoi SuperJet-100
     2 | Airbus A319-100
     2 | Airbus A320-200
     2 | Airbus A321-200
     2 | Boeing 737-300
     2 | Boeing 767-300
     3 | Boeing 777-300
(9 rows)

demo=# explain(costs off) select class, model from aircrafts_v order by class, model;
                       QUERY PLAN                      
--------------------------------------------------------
 Index Scan using aircrafts_case_model_idx on aircrafts
(1 row)

Точно так же можно выполнить запрос с сортировкой по убыванию:

demo=# select class, model from aircrafts_v order by class desc, model desc;
 class |        model        
-------+---------------------
     3 | Boeing 777-300
     2 | Boeing 767-300
     2 | Boeing 737-300
     2 | Airbus A321-200
     2 | Airbus A320-200
     2 | Airbus A319-100
     1 | Sukhoi SuperJet-100
     1 | Cessna 208 Caravan
     1 | Bombardier CRJ-200
(9 rows)

demo=# explain(costs off)
select class, model from aircrafts_v order by class desc, model desc;
                           QUERY PLAN                            
-----------------------------------------------------------------
 Index Scan Backward using aircrafts_case_model_idx on aircrafts
(1 row)

Но из этого индекса невозможно получить данные, отсортированные по одному столбцу по убыванию, а по другому — по возрастанию. Для этого потребуется отдельно выполнить сортировку:

demo=# explain(costs off)
select class, model from aircrafts_v order by class asc, model desc;
                   QUERY PLAN                    
-------------------------------------------------
 Sort
   Sort Key: (CASE ... END), aircrafts.model DESC
   ->  Seq Scan on aircrafts
(3 rows)

(Заметьте, что с горя планировщик выбрал сканирование таблицы, даже несмотря на установку enable_seqscan = off, сделанную ранее. Это потому, что на самом деле она не запрещает сканирование таблицы, а только устанавливает ему запредельную стоимость — посмотрите план с «costs on».)

Чтобы такой запрос мог быть выполнен с использованием индекса, индекс надо построить с сортировкой в нужном порядке:

demo=# create index aircrafts_case_asc_model_desc_idx on aircrafts(
(case when range < 4000 then 1 when range < 10000 then 2 else 3 end) asc, model desc);
CREATE INDEX

demo=# explain(costs off)
select class, model from aircrafts_v order by class asc, model desc;
                           QUERY PLAN                            
-----------------------------------------------------------------
 Index Scan using aircrafts_case_asc_model_desc_idx on aircrafts
(1 row)


Порядок столбцов

Другой вопрос, который встает при использовании многоколоночных индексов — порядок перечисления столбцов в индексе. В случае B-дерева этот порядок имеет огромное значение: данные внутри страниц будут отсортированы сначала по первому полю, затем по второму и так далее.

Индекс, который мы построили по интервалам дальностей и моделям, можно условно представить таким образом:



Конечно, на самом деле такой небольшой индекс поместится в одну корневую страницу; на рисунке он искусственно распределен на несколько страниц для наглядности.

Из этой схемы понятно, что поиск будет работать эффективно с такими, например, предикатами, как «class = 3» (поиск только по первому полю) или «class = 3 and model = 'Boeing 777-300'» (поиск по обоим полям).

А вот поиск по предикату «model = 'Boeing 777-300'» будет куда менее эффективным: начиная с корня, мы не можем определить, в какой из дочерних узлов спускаться, поэтому спускаться придется во все. Это не значит, что такой индекс не может использоваться в принципе — вопрос только в эффективности. Например, если бы у нас было три класса самолетов и очень много моделей в каждом классе, то нам пришлось бы просмотреть примерно треть индекса, и это могло бы оказаться эффективнее, чем полное сканирование таблицы. А могло бы и не оказаться.

Зато если создать индекс таким образом:

demo=# create index on aircrafts(
model, (case when range < 4000 then 1 when range < 10000 then 2 else 3 end));
CREATE INDEX

то порядок полей поменяется:



И с таким индексом поиск по предикату «model = 'Boeing 777-300'» будет выполняться эффективно, а по предикату «class = 3» — нет.

Неопределенные значения

Метод доступа btree индексирует неопределенные значения и поддерживает поиск по условиям is null и is not null.

Возьмем таблицу рейсов, в которой встречаются неопределенные значения:

demo=# create index on flights(actual_arrival);
CREATE INDEX
demo=# explain(costs off) select * from flights where actual_arrival is null;
                      QUERY PLAN                      
-------------------------------------------------------
 Bitmap Heap Scan on flights
   Recheck Cond: (actual_arrival IS NULL)
   ->  Bitmap Index Scan on flights_actual_arrival_idx
         Index Cond: (actual_arrival IS NULL)
(4 rows)

Неопределенные значения располагаются с одного или другого края листовых узлов в зависимости от того, как был создан индекс (nulls first или nulls last). Это важно, если в запросе участвует сортировка: порядок расположения неопределенных значений в индексе и в порядке сортировки должны совпадать, чтобы индекс можно было использовать.
В этом примере порядки совпадают, поэтому индекс может использоваться:

demo=# explain(costs off) select * from flights order by actual_arrival nulls last;
                       QUERY PLAN                      
--------------------------------------------------------
 Index Scan using flights_actual_arrival_idx on flights
(1 row)

А здесь порядки отличаются, и оптимизатор выбирает сканирование таблицы и сортировку:

demo=# explain(costs off) select * from flights order by actual_arrival nulls first;
               QUERY PLAN              
----------------------------------------
 Sort
   Sort Key: actual_arrival NULLS FIRST
   ->  Seq Scan on flights
(3 rows)

Чтобы индекс мог использоваться, надо создать его так, чтобы неопределенные значения шли в начале:

demo=# create index flights_nulls_first_idx on flights(actual_arrival nulls first);
CREATE INDEX
demo=# explain(costs off) select * from flights order by actual_arrival nulls first;
                     QUERY PLAN                      
-----------------------------------------------------
 Index Scan using flights_nulls_first_idx on flights
(1 row)

Причина таких неувязок, конечно, в том, что неопределенные значения не являются сортируемыми: результат сравнения неопределенного значения с любым другим не определен:

demo=# \pset null NULL
Null display is "NULL".
demo=# select null < 42;
 ?column?
----------
 NULL
(1 row)

Это идет вразрез с сущностью B-дерева и не укладывается в общую схему. Но неопределенные значения играют такую важную роль в базах данных, что для них все время приходится делать исключения.

Следствием того, что неопределенные значения индексируются, является возможность использовать индекс, даже если на таблицу не наложено вообще никаких условий (поскольку в индексе гарантированно содержится информация обо всех строках таблицы). Это может иметь смысл, если в запросе нужно упорядочить данные и индекс обеспечивает нужный порядок. Тогда планировщик может предпочесть индексный доступ, чтобы сэкономить на отдельной сортировке.

Свойства

Посмотрим свойства метода доступа btree (запросы приводились ранее).

 amname |     name      | pg_indexam_has_property
--------+---------------+-------------------------
 btree  | can_order     | t
 btree  | can_unique    | t
 btree  | can_multi_col | t
 btree  | can_exclude   | t

Как мы видели, B-дерево может упорядочивать данные и поддерживает уникальность — и это единственный метод доступа, который обеспечивает такие свойства. Индексы по нескольким столбцам также допустимы; но это умеют и другие методы (хотя и не все). Про поддержку ограничений exclude мы, не без причины, поговорим в следующий раз.

     name      | pg_index_has_property
---------------+-----------------------
 clusterable   | t
 index_scan    | t
 bitmap_scan   | t
 backward_scan | t

Метод доступа b-tree поддерживает оба способа получения значений: и индексное сканирование, и сканирование битовой карты. И, как мы видели, умеет обходить дерево как «вперед», так и в обратном направлении.

        name        | pg_index_column_has_property
--------------------+------------------------------
 asc                | t
 desc               | f
 nulls_first        | f
 nulls_last         | t
 orderable          | t
 distance_orderable | f
 returnable         | t
 search_array       | t
 search_nulls       | t

Первые четыре свойства этого уровня говорят о том, как именно упорядочены значения данного конкретного столбца. В этом примере значения отсортированы по возрастанию (asc), а неопределенные значения находятся к конце (nulls_last). Но, как мы видели, могут быть и другие комбинации.

Свойство search_array говорит о том, что индекс поддерживает такие конструкции:

demo=# explain(costs off)
select * from aircrafts where aircraft_code in ('733','763','773');
                           QUERY PLAN                            
-----------------------------------------------------------------
 Index Scan using aircrafts_pkey on aircrafts
   Index Cond: (aircraft_code = ANY ('{733,763,773}'::bpchar[]))
(2 rows)

Свойство returnable говорит о поддержке исключительно индексного сканирования — что логично, ведь в индексных записях хранятся сами проиндексированные значения (в отличие от хеш-индекса, например). Тут уместно сказать несколько слов об особенностях покрывающих индексов на основе B-дерева.

Уникальные индексы с дополнительными столбцами

Как мы говорили ранее, покрывающим называется индекс, который содержит все значения, необходимые в запросе; при этом обращение к самой таблице уже не требуется (почти). В том числе покрывающим может быть и уникальный индекс.

Но допустим, мы хотим добавить к уникальному индексу дополнительные столбцы, необходимые в запросе. Значения нового составного ключа уже могут быть и не уникальными, и тогда потребуется иметь два индекса практически по одним и тем же столбцам: один уникальный (для поддержки ограничения целостности) и еще один не уникальный (в качестве покрывающего). Это, конечно, неэффективно.

В нашей компании Анастасия Лубенникова lubennikovaav доработала метод btree так, чтобы в уникальный индекс можно было включать дополнительные — неуникальные — столбцы. Надеемся, что этот патч будет принят сообществом и войдет в PostgreSQL, но это случится уже не в версии 10. Пока патч доступен в Postgres Pro Standard 9.5+, и вот как это выглядит.

Возьмем таблицу бронирований:

demo=# \d bookings
              Table "bookings.bookings"
    Column    |           Type           | Modifiers
--------------+--------------------------+-----------
 book_ref     | character(6)             | not null
 book_date    | timestamp with time zone | not null
 total_amount | numeric(10,2)            | not null
Indexes:
    "bookings_pkey" PRIMARY KEY, btree (book_ref)
Referenced by:
    TABLE "tickets" CONSTRAINT "tickets_book_ref_fkey" FOREIGN KEY (book_ref) REFERENCES bookings(book_ref)

В ней первичный ключ (book_ref, код бронирования) поддержан обычным btree-индексом. Создадим новый уникальный индекс с дополнительным столбцом:

demo=# create unique index bookings_pkey2 on bookings(book_ref) include (book_date);
CREATE INDEX

Теперь заменим существующий индекс на новый (в транзакции, чтобы все изменения вступили в силу одновременно):

demo=# begin;
BEGIN
demo=# alter table bookings drop constraint bookings_pkey cascade;
NOTICE:  drop cascades to constraint tickets_book_ref_fkey on table tickets
ALTER TABLE
demo=# alter table bookings add primary key using index bookings_pkey2;
ALTER TABLE
demo=# alter table tickets add foreign key (book_ref) references bookings (book_ref);
ALTER TABLE
demo=# commit;
COMMIT

Вот что получилось:

demo=# \d bookings
              Table "bookings.bookings"
    Column    |           Type           | Modifiers
--------------+--------------------------+-----------
 book_ref     | character(6)             | not null
 book_date    | timestamp with time zone | not null
 total_amount | numeric(10,2)            | not null
Indexes:
    "bookings_pkey2" PRIMARY KEY, btree (book_ref) INCLUDE (book_date)
Referenced by:
    TABLE "tickets" CONSTRAINT "tickets_book_ref_fkey" FOREIGN KEY (book_ref) REFERENCES bookings(book_ref)

Теперь один и тот же индекс работает и как уникальный, и выступает покрывающим для такого, например, запроса:

demo=# explain(costs off)
select book_ref, book_date from bookings where book_ref = '059FC4';
                    QUERY PLAN                    
--------------------------------------------------
 Index Only Scan using bookings_pkey2 on bookings
   Index Cond: (book_ref = '059FC4'::bpchar)
(2 rows)


Создание индекса

Хорошо известный, но от этого не менее важный факт: загрузку в таблицу большого объема данных лучше выполнять без индексов, а необходимые индексы создавать уже после. Это не только быстрее, но и сам индекс скорее всего получится меньшего размера.

Дело в том, что при создании btree-индекса используется более эффективная процедура, чем построчная вставка значений в дерево. Грубо говоря, все имеющиеся в таблице данные сортируются и из них формируются листовые страницы индекса; затем на это основание «наращиваются» внутренние страницы до тех пор, пока вся пирамида не сойдется к корню.

Скорость этого процесса зависит от размера доступной оперативной памяти, который ограничен параметром maintenance_work_mem, так что увеличение значения может привести к ускорению. В случае уникальных индексов в дополнение к maintenance_work_mem выделяется еще память размером work_mem.

Семантика сравнения

В прошлый раз мы говорили о том, что PostgreSQL должен знать, какие хеш-функции вызывать для значений разных типов, и что такое соответствие хранится в метода доступа hash. Точно так же системе надо понимать, как упорядочивать значения — это нужно для сортировок, группировок (иногда), соединения слиянием и т. п. PostgreSQL не привязывается к именам операторов (таким, как >, <, =), потому что пользователь вполне может определить свой тип данных и назвать соответствующие операторы как-то иначе. Вместо этого имена операторов определяются семейством операторов, привязанных к методу доступа btree.

Например, вот какие операторы сравнения используются в семействе bool_ops:

postgres=# select   amop.amopopr::regoperator as opfamily_operator,
         amop.amopstrategy
from     pg_am am,
         pg_opfamily opf,
         pg_amop amop
where    opf.opfmethod = am.oid
and      amop.amopfamily = opf.oid
and      am.amname = 'btree'
and      opf.opfname = 'bool_ops'
order by amopstrategy;

  opfamily_operator  | amopstrategy
---------------------+--------------
 <(boolean,boolean)  |            1
 <=(boolean,boolean) |            2
 =(boolean,boolean)  |            3
 >=(boolean,boolean) |            4
 >(boolean,boolean)  |            5
(5 rows)

Здесь мы видим пять операторов сравнения, но, как было сказано, не должны ориентироваться на их названия. Чтобы понять, какое сравнение реализовано каким оператором, вводится понятие стратегии. Для btree определены пять стратегий, определяющих семантику операторов:

• 1 — меньше;
• 2 — меньше либо равно;
• 3 — равно;
• 4 — больше либо равно;
• 5 — больше.

Некоторые семейства могут содержать несколько операторов, реализующих одну стратегию. Например, вот какие операторы есть в семействе integer_ops для стратегии 1:

postgres=# select   amop.amopopr::regoperator as opfamily_operator
from     pg_am am,
         pg_opfamily opf,
         pg_amop amop
where    opf.opfmethod = am.oid
and      amop.amopfamily = opf.oid
and      am.amname = 'btree'
and      opf.opfname = 'integer_ops'
and      amop.amopstrategy = 1
order by opfamily_operator;

  opfamily_operator  
----------------------
 <(integer,bigint)
 <(smallint,smallint)
 <(integer,integer)
 <(bigint,bigint)
 <(bigint,integer)
 <(smallint,integer)
 <(integer,smallint)
 <(smallint,bigint)
 <(bigint,smallint)
(9 rows)

За счет этого оптимизатор имеет возможность сравнивать значения разных типов, входящих в одно семейство, не прибегая к приведению.

Индексная поддержка для нового типа данных

В документации есть пример создания нового типа данных для комплексных чисел, и класса операторов для сортировки значений этого типа. Этот пример использует язык Си, что абсолютно оправдано, когда важна скорость. Но ничто не мешает проделать тот же эксперимент на чистом SQL, просто чтобы попробовать и лучше разобраться в семантике сравнения.

Создаем новый составной тип с двумя полями: действительная и мнимая части.

postgres=# create type complex as (re float, im float);
CREATE TYPE

Можно создать таблицу с полем нового типа и добавить в нее каких-нибудь значений:

postgres=# create table numbers(x complex);
CREATE TABLE
postgres=# insert into numbers values ((0.0, 10.0)), ((1.0, 3.0)), ((1.0, 1.0));
INSERT 0 3

Теперь возникает вопрос: как упорядочивать комплексные числа, если в математическом смысле для них не определено отношение порядка?

Как выясняется, операции сравнения уже определены за нас:

postgres=# select * from numbers order by x;
   x    
--------
 (0,10)
 (1,1)
 (1,3)
(3 rows)

По умолчанию составной тип сортируется покомпонентно: сначала сравниваются первые поля, затем вторые и так далее, примерно как посимвольно сравниваются текстовые строки. Но можно определить и другой порядок. Например, комплексные числа можно рассматривать как векторы и упорядочивать их по модулю (по длине), который вычисляется как корень из суммы квадратов координат (теорема Пифагора). Чтобы определить такой порядок, создадим вспомогательную функцию для вычисления модуля:

postgres=# create function modulus(a complex) returns float as $$
    select sqrt(a.re*a.re + a.im*a.im);
$$ immutable language sql;
CREATE FUNCTION

И с ее помощью методично определим функции для всех пяти операций сравнения:

postgres=# create function complex_lt(a complex, b complex) returns boolean as $$
    select modulus(a) < modulus(b);
$$ immutable language sql;
CREATE FUNCTION
postgres=# create function complex_le(a complex, b complex) returns boolean as $$
    select modulus(a) <= modulus(b);
$$ immutable language sql;
CREATE FUNCTION
postgres=# create function complex_eq(a complex, b complex) returns boolean as $$
    select modulus(a) = modulus(b);
$$ immutable language sql;
CREATE FUNCTION
postgres=# create function complex_ge(a complex, b complex) returns boolean as $$
    select modulus(a) >= modulus(b);
$$ immutable language sql;
CREATE FUNCTION
postgres=# create function complex_gt(a complex, b complex) returns boolean as $$
    select modulus(a) > modulus(b);
$$ immutable language sql;
CREATE FUNCTION

И создадим соответствующие операторы. Чтобы показать, что они не обязаны называться «>», «<» и так далее, дадим им «странные» имена.

postgres=# create operator #<#(leftarg=complex, rightarg=complex, procedure=complex_lt);
CREATE OPERATOR
postgres=# create operator #<=#(leftarg=complex, rightarg=complex, procedure=complex_le);
CREATE OPERATOR
postgres=# create operator #=#(leftarg=complex, rightarg=complex, procedure=complex_eq);
CREATE OPERATOR
postgres=# create operator #>=#(leftarg=complex, rightarg=complex, procedure=complex_ge);
CREATE OPERATOR
postgres=# create operator #>#(leftarg=complex, rightarg=complex, procedure=complex_gt);
CREATE OPERATOR

На этом этапе уже можно сравнивать числа:

postgres=# select (1.0,1.0)::complex #<# (1.0,3.0)::complex;
 ?column?
----------
 t
(1 row)

Кроме пяти операторов метод доступа btree требует определить еще одну (избыточную, но удобную) функцию: она должна возвращать -1, 0 или 1 если первое значение меньше, равно или больше второго. Такая вспомогательная функция называется опорной; другие методы доступа могут требовать создания других опорных функций.

postgres=# create function complex_cmp(a complex, b complex) returns integer as $$
    select case when modulus(a) < modulus(b) then -1
                when modulus(a) > modulus(b) then 1
                else 0
           end;
$$ language sql;
CREATE FUNCTION

Теперь мы готовы создать класс операторов (а одноименное семейство будет создано автоматически):

postgresx=# create operator class complex_ops
default for type complex
using btree as
    operator 1 #<#,
    operator 2 #<=#,
    operator 3 #=#,
    operator 4 #>=#,
    operator 5 #>#,
    function 1 complex_cmp(complex,complex);
CREATE OPERATOR CLASS

Теперь сортировка работает так, как мы хотели:

postgres=# select * from numbers order by x;
   x    
--------
 (1,1)
 (1,3)
 (0,10)
(3 rows)

И, разумеется, она будет поддерживаться индексом btree.

Для полноты картины, опорные функции можно увидеть таким запросом:

postgres=# select amp.amprocnum,
       amp.amproc,
       amp.amproclefttype::regtype,
       amp.amprocrighttype::regtype
from   pg_opfamily opf,
       pg_am am,
       pg_amproc amp
where  opf.opfname = 'complex_ops'
and    opf.opfmethod = am.oid
and    am.amname = 'btree'
and    amp.amprocfamily = opf.oid;

 amprocnum |   amproc    | amproclefttype | amprocrighttype
-----------+-------------+----------------+-----------------
         1 | complex_cmp | complex        | complex
(1 row)


Внутренности

Внутреннюю структуру B-дерева можно изучать, используя расширение pageinspect.

demo=# create extension pageinspect;
CREATE EXTENSION

Метастраница индекса:

demo=# select * from bt_metap('ticket_flights_pkey');
 magic  | version | root | level | fastroot | fastlevel
--------+---------+------+-------+----------+-----------
 340322 |       2 |  164 |     2 |      164 |         2
(1 row)

Самое интересное здесь — глубина индекса (level): для размещения индекса по двум столбцам для таблицы с миллионом строк потребовалось всего 2 уровня (не считая корня).

Статистическая информация о блоке 164 (корень):

demo=# select type, live_items, dead_items, avg_item_size, page_size, free_size
from bt_page_stats('ticket_flights_pkey',164);
 type | live_items | dead_items | avg_item_size | page_size | free_size
------+------------+------------+---------------+-----------+-----------
 r    |         33 |          0 |            31 |      8192 |      6984
(1 row)

И сами данные в блоке (в поле data, которое тут принесено в жертву ширине экрана, находится значение ключа индексирования в двоичном виде):

demo=# select itemoffset, ctid, itemlen, left(data,56) as data
from bt_page_items('ticket_flights_pkey',164) limit 5;
 itemoffset |  ctid   | itemlen |                           data                          
------------+---------+---------+----------------------------------------------------------
          1 | (3,1)   |       8 |
          2 | (163,1) |      32 | 1d 30 30 30 35 34 33 32 33 30 35 37 37 31 00 00 ff 5f 00
          3 | (323,1) |      32 | 1d 30 30 30 35 34 33 32 34 32 33 36 36 32 00 00 4f 78 00
          4 | (482,1) |      32 | 1d 30 30 30 35 34 33 32 35 33 30 38 39 33 00 00 4d 1e 00
          5 | (641,1) |      32 | 1d 30 30 30 35 34 33 32 36 35 35 37 38 35 00 00 2b 09 00
(5 rows)

Первый элемент носит технический характер и задает верхнюю границу значения ключа всех элементов блока (деталь реализации, про которую мы не говорили), а собственно данные начинаются со второго элемента. Видно, что самым левым дочерним узлом является блок 163, затем идет блок 323 и так далее. Которые, в свою очередь, тоже можно изучить с помощью этих же функций.

Дальше, по доброй традиции, имеет смысл читать документацию, README и исходный код.

И еще одно потенциально полезное расширение: amcheck, которое войдет в состав PostgreSQL 10, а для более ранних версий его можно взять на github. Это расширение проверяет логическую согласованность данных в B-деревьях и позволяет заблаговременно обнаружить повреждения.

Продолжение следует.