Содержание

• Часть 1: Введение
  
• Часть 2: Manifold learning и скрытые (latent) переменные
  
• Часть 3: Вариационные автоэнкодеры (VAE)
  
• Часть 4: Conditional VAE
  
• Часть 5: GAN (Generative Adversarial Networks) и tensorflow
  
• Часть 6: VAE + GAN
  

В прошлой части мы уже обсуждали, что такое скрытые переменные, взглянули на их распределение, а также поняли, что из распределения скрытых переменных в обычных автоэнкодерах сложно генерировать новые объекты. Для того чтобы можно было генерировать новые объекты, пространство скрытых переменных (latent variables) должно быть предсказуемым.

Вариационные автоэнкодеры (Variational Autoencoders) — это автоэнкодеры, которые учатся отображать объекты в заданное скрытое пространство и, соответственно, сэмплить из него. Поэтому вариационные автоэнкодеры относят также к семейству генеративных моделей.



Иллюстрация из [2]

Имея какое-то одно распределение , можно получить произвольное другое , например, пусть — обычное нормальное распределение, — тоже случайное распределение, но выглядит совсем по-другому




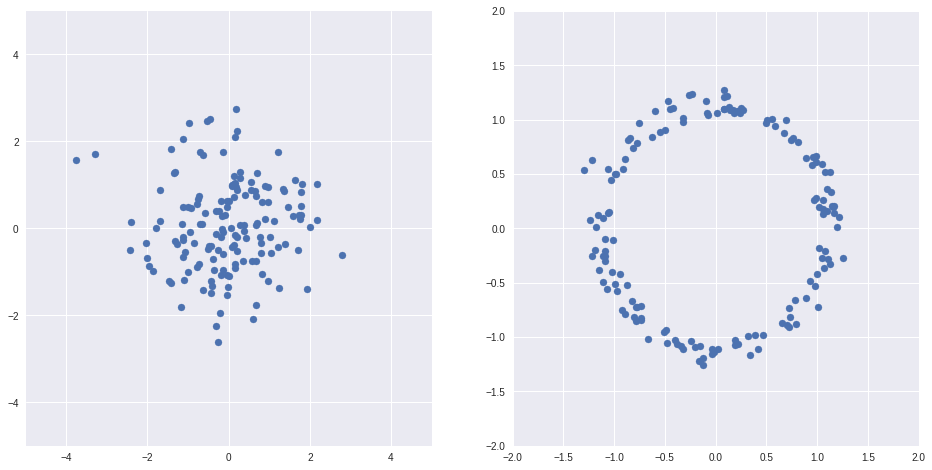
Пример выше из [1]

Таким образом, если подобрать правильные функции, то можно отобразить пространства скрытых переменных обычных автоэнкодеров в какие-то хорошие пространства, например, такие, где распределение нормально. А потом обратно.

С другой стороны, специально учиться отображать одни скрытые пространства в другие вовсе не обязательно. Если есть какие-то полезные скрытые пространства, то правильный автоэнкодер научится им по пути сам, но отображать, в конечном итоге, будет в нужное нам пространство.

---

Ниже непростая, но необходимая теория лежащая в основе VAE. Постарался выжать из [1, Tutorial on Variational Autoencoders, Carl Doersch, 2016] все самое принципиальное, остановившись подробнее на тех местах, которые показались сложными мне самому.

Пусть — скрытые переменные, а — данные. На примере нарисованных цифр рассмотрим естественный генеративный процесс, который сгенерировал нашу выборку:

• вероятностное распределение изображений цифр на картинках, т.е. вероятность конкретного изображения цифры в принципе быть нарисованным (если картинка не похожа на цифру, то эта вероятность крайне мала, и наоборот),
  
• — вероятностное распределение скрытых факторов, например, распределение толщины штриха,
  
• — распределение вероятности картинок при заданных скрытых факторах, одни и те же факторы могут привести к разным картинкам (один и тот же человек в одних и тех же условиях не рисует абсолютно одинаковые цифры).
  

Представим как сумму некоторой генерирующей функции и некоторого сложного шума


Мы хотим построить некоторый искусственный генеративный процесс, который будет создавать объекты, близкие в некоторой метрике к тренировочным .


и снова


— некоторое семейство функций, которое представляет наша модель, а — ее параметры. Выбирая метрику, мы выбираем то, какого вида нам представляется шум . Если метрика , то мы считаем шум нормальным и тогда:


По принципу максимального правдоподобия нам остается оптимизировать параметры , для того чтобы максимизировать , т.е. вероятность появления объектов из выборки.

Проблема в том, что оптимизировать интеграл (1) напрямую мы не можем: пространство может быть высокоразмерное, объектов много, да и метрика плохая. С другой стороны, если задуматься, то к каждому конкретному может привести лишь очень небольшое подмножество , для остальных же будет очень близок к нулю.
И при оптимизации достаточно сэмплить только из хороших .

Для того чтобы знать, из каких нам надо сэмплить, введем новое распределение , которое в зависимости от будет показывать распределение , которое могло привести к этому .

Запишем сперва расстояние Кульбака-Лейблера (несимметричная мера «похожести» двух распределений, подробнее [3] ) между
и реальным :


Применяем формулу Байеса:


Выделяем еще одно расстояние Кульбака-Лейблера:


В итоге получаем тождество:

---

---

Это тождество — краеугольный камень вариационных автоэнкодеров, оно верно для любых и .

Пусть и зависят от параметров: и , а — нормальное , тогда получаем:


Взглянем повнимательнее на то, что у нас получилось:

• во-первых, , подозрительно похожи на энкодер и декодер (точнее декодер это в выражении ),
  
• слева в тождестве — значение, которое мы хотим максимизировать для элементов нашей тренировочной выборки + некоторая ошибка , которая, будем надеяться, при достаточной емкости уйдет в 0,
  
• справа значение, которое мы можем оптимизировать градиентным спуском, где первый член имеет смысл качества предсказания декодером по значениям , а второй член, это расстояние К-Л между распределением , которое предсказывает энкодер для конкретного , и распределением для всех сразу.
  

Для того, чтобы иметь возможность оптимизировать правую часть градиентным спуском, осталось разобраться с двумя вещами:

1. Точнее определим что такое

Обычно выбирается нормальным распределением:


То есть энкодер для каждого предсказывает 2 значения: среднее и вариацию нормального распределения, из которого уже сэмплируются значения. Работает это все примерно вот так:



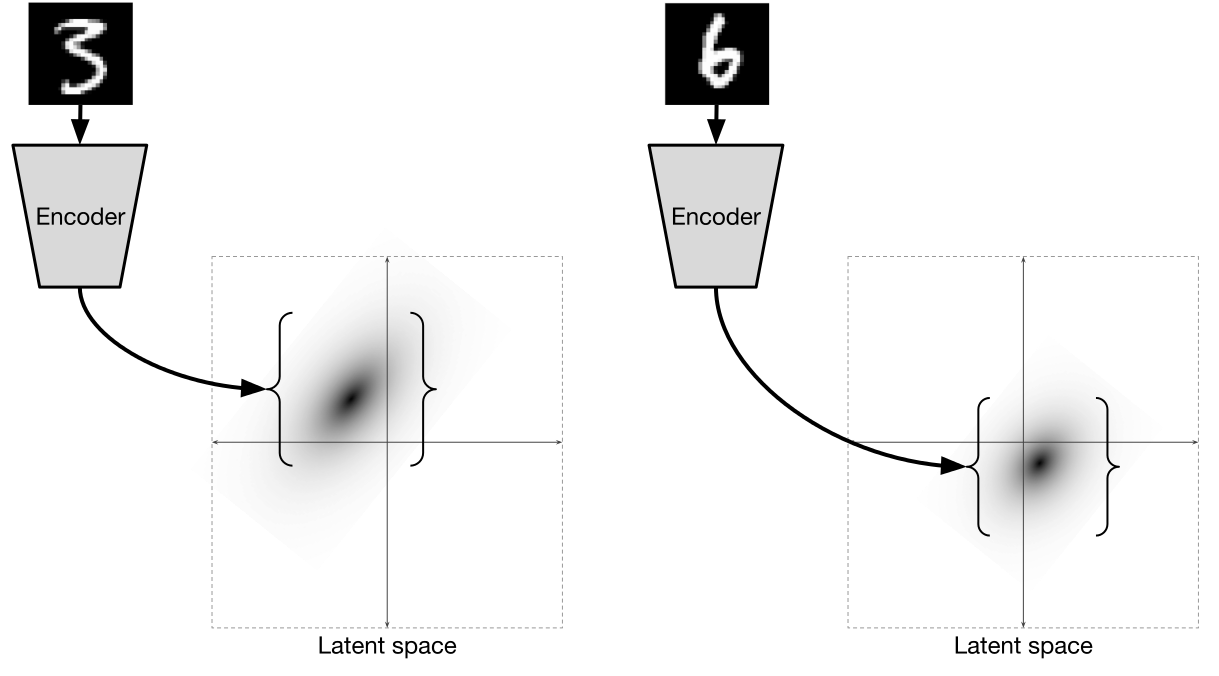
Иллюстрация из [2]

При том, что для каждой отдельной точки данных энкодер предсказывает некоторое нормальное распределение


для маргинального распределения : , что получается из формулы, и это потрясающе.



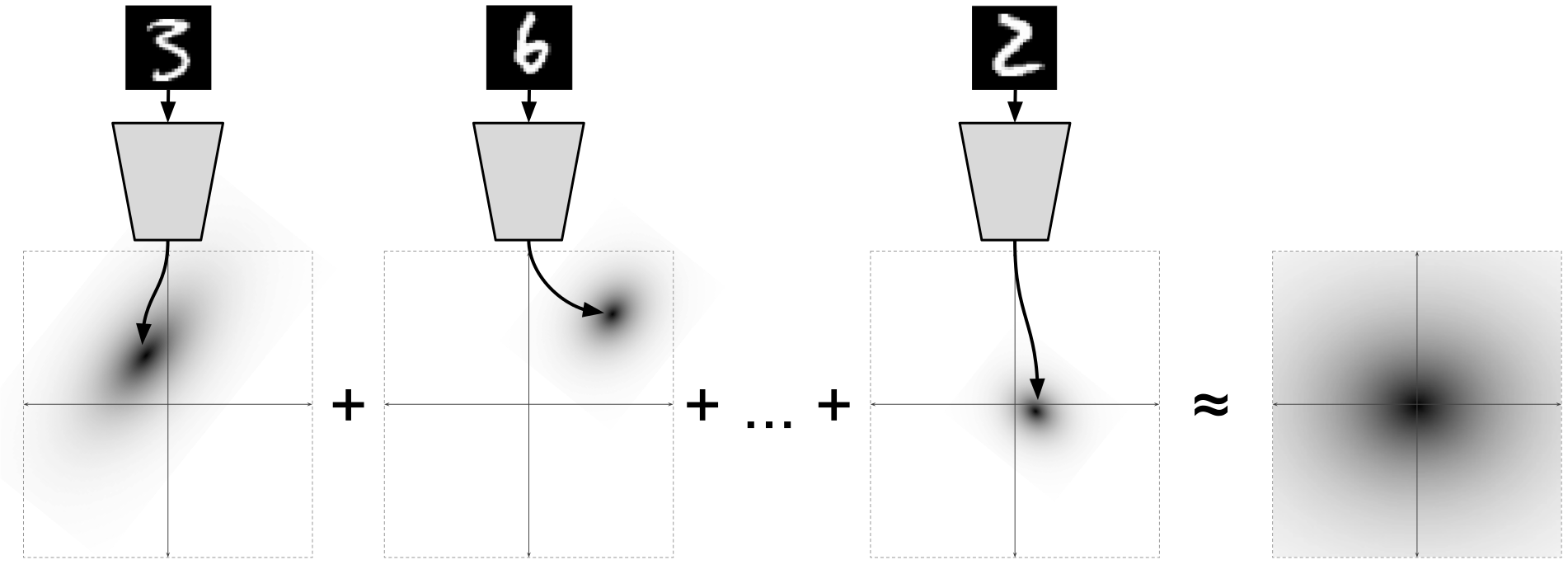
Иллюстрация из [2]

При этом принимает вид:

2. Разберемся с тем, как распространять ошибки через

Дело в том, что здесь мы берем случайные значения и передаем их в декодер.
Ясно, что распространять ошибки через случайные значения напрямую нельзя, поэтому используется так называемый трюк с репараметризацией (reparametrization trick).

Схема получается вот такая:


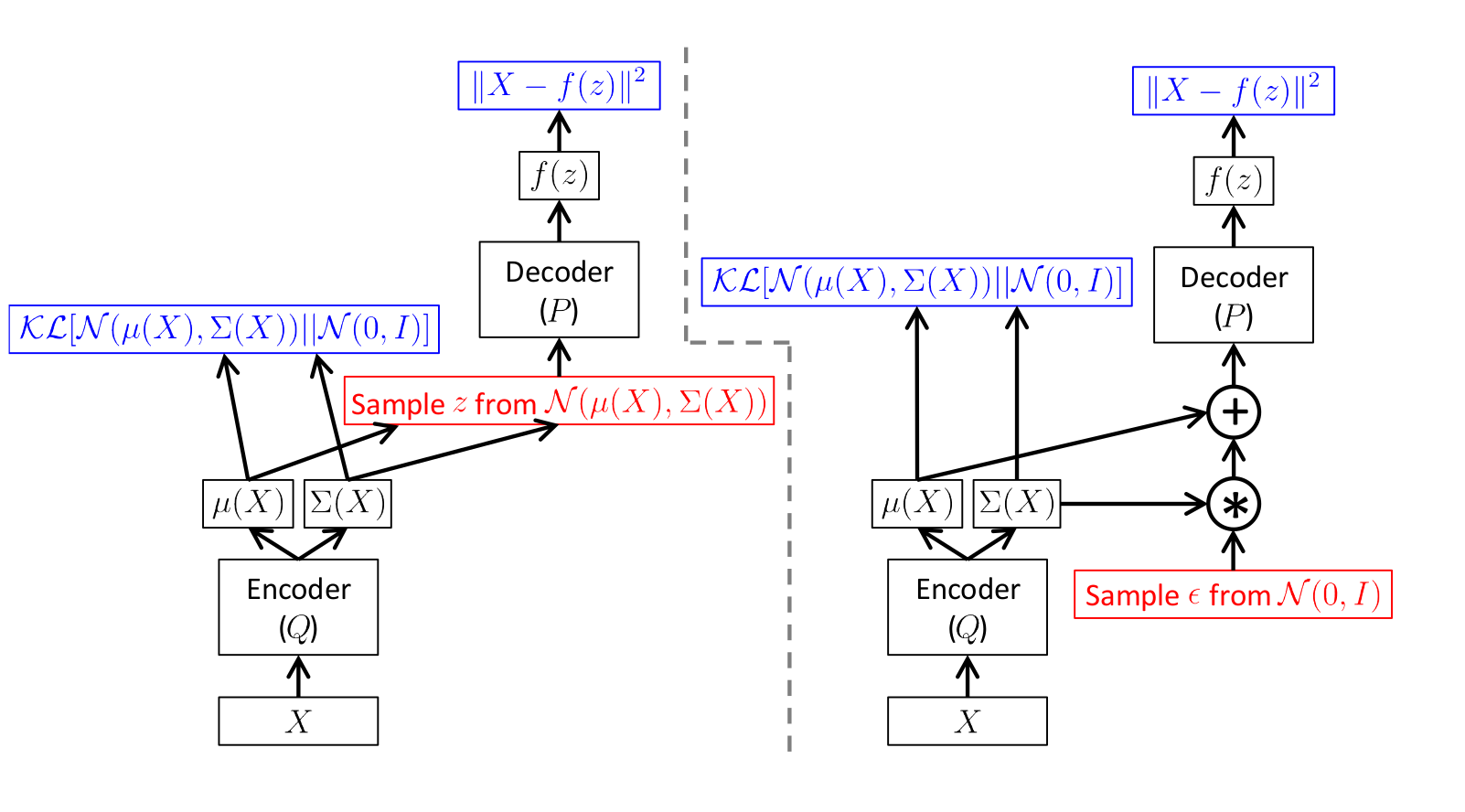
Иллюстрация из [1]

Здесь на левой картинке схема без трюка, а на правой с трюком.
Красным цветом показано семплирование, а синим вычисление ошибки.
То есть по сути просто берем предсказанное энкодером стандартное отклонение умножаем на случайное число из и добавляем предсказанное среднее .
Прямое распространение на обеих схемах абсолютно одинаковое, однако на правой схеме работает обратное распространение ошибки.

После того как мы обучили такой вариационный автоэнкодер, декодер становится полноправной генеративной моделью. По сути и энкодер-то нужен в основном для того, чтобы обучить декодер отдельно быть генеративной моделью.


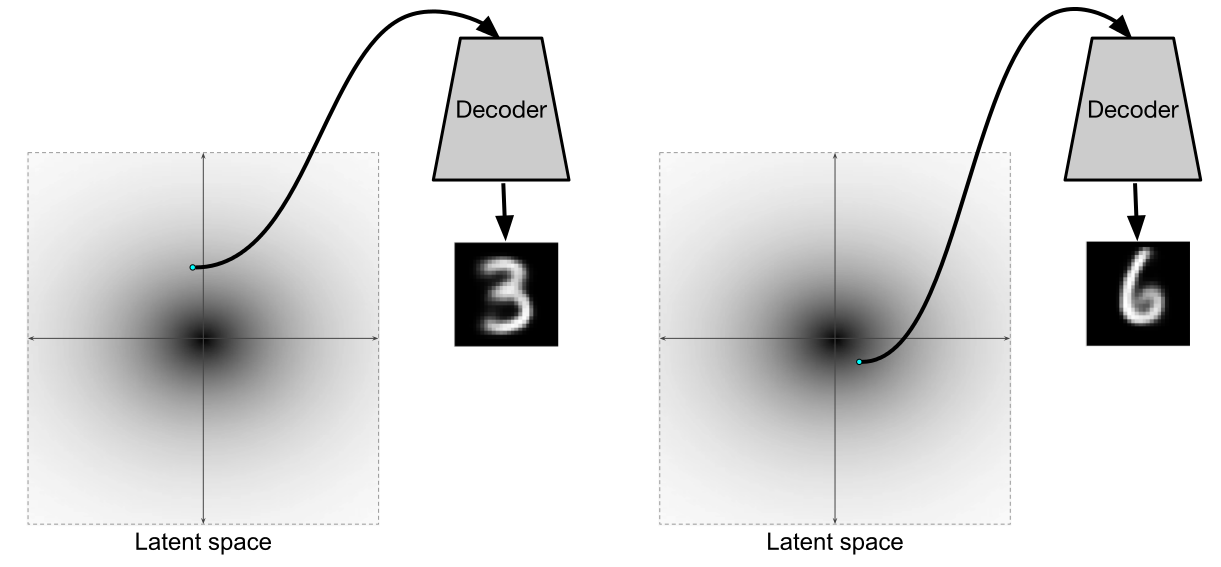
Иллюстрация из [2]

Иллюстрация из [1]

Но то, что энкодер и декодер вместо образуют еще и полноценный автоэнкодер — очень приятный плюс.

VAE в Keras

Теперь, когда мы разобрались в том, что такое вариационные автоэнкодеры, напишем такой на Keras.

Импортируем необходимые библиотеки и датасет:

import sys
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns

from keras.datasets import mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()

x_train = x_train.astype('float32') / 255.
x_test  = x_test .astype('float32') / 255.
x_train = np.reshape(x_train, (len(x_train), 28, 28, 1))
x_test  = np.reshape(x_test,  (len(x_test),  28, 28, 1))

Зададим основные параметры. Скрытое пространство возьмем размерности 2, чтобы позже генерировать из него и визуализировать результат.
Замечание: размерность 2 крайне мала, поэтому следует ожидать, что цифры получатся очень размытыми.

batch_size = 500
latent_dim = 2
dropout_rate = 0.3
start_lr = 0.0001

Напишем модели вариационного автоэнкодера.

Для того чтобы обучение происходило быстрее и более качественно, добавим слои dropout и batch normalization.

А в декодере используем в качестве активации leaky ReLU, которую добавляем отдельным слоем после dense слоев без активации.
Функция sampling реализует сэмплирование значений из с использованием трюка репараметризации.

vae_loss это правая часть из уравнения:
далее будет использоваться в качестве лосса.

from keras.layers import Input, Dense 
from keras.layers import BatchNormalization, Dropout, Flatten, Reshape, Lambda
from keras.models import Model

from keras.objectives import binary_crossentropy
from keras.layers.advanced_activations import LeakyReLU
from keras import backend as K

def create_vae():
    models = {}

    # Добавим Dropout и BatchNormalization
    def apply_bn_and_dropout(x):
        return Dropout(dropout_rate)(BatchNormalization()(x))

    # Энкодер
    input_img = Input(batch_shape=(batch_size, 28, 28, 1))
    x = Flatten()(input_img)
    x = Dense(256, activation='relu')(x)
    x = apply_bn_and_dropout(x)
    x = Dense(128, activation='relu')(x)
    x = apply_bn_and_dropout(x)

    # Предсказываем параметры распределений
    # Вместо того, чтобы предсказывать стандартное отклонение, предсказываем логарифм вариации
    z_mean = Dense(latent_dim)(x)
    z_log_var = Dense(latent_dim)(x)

    # Сэмплирование из Q с трюком репараметризации
    def sampling(args):
        z_mean, z_log_var = args
        epsilon = K.random_normal(shape=(batch_size, latent_dim), mean=0., stddev=1.0)
        return z_mean + K.exp(z_log_var / 2) * epsilon
    l = Lambda(sampling, output_shape=(latent_dim,))([z_mean, z_log_var])

    models["encoder"]  = Model(input_img, l, 'Encoder') 
    models["z_meaner"] = Model(input_img, z_mean, 'Enc_z_mean')
    models["z_lvarer"] = Model(input_img, z_log_var, 'Enc_z_log_var')

    # Декодер
    z = Input(shape=(latent_dim, ))
    x = Dense(128)(z)
    x = LeakyReLU()(x)
    x = apply_bn_and_dropout(x)
    x = Dense(256)(x)
    x = LeakyReLU()(x)
    x = apply_bn_and_dropout(x)
    x = Dense(28*28, activation='sigmoid')(x)
    decoded = Reshape((28, 28, 1))(x)

    models["decoder"] = Model(z, decoded, name='Decoder')
    models["vae"]     = Model(input_img, models["decoder"](models["encoder"](input_img)), name="VAE")

    def vae_loss(x, decoded):
        x = K.reshape(x, shape=(batch_size, 28*28))
        decoded = K.reshape(decoded, shape=(batch_size, 28*28))
        xent_loss = 28*28*binary_crossentropy(x, decoded)
        kl_loss = -0.5 * K.sum(1 + z_log_var - K.square(z_mean) - K.exp(z_log_var), axis=-1)
        return (xent_loss + kl_loss)/2/28/28

    return models, vae_loss

models, vae_loss = create_vae()
vae = models["vae"]

Замечание: мы использовали Lambda-слой с функцией, сэмплирующей из из нижележащего фреймворка, которая явно требует размер батча. Во всех моделях, в которых присутствует этот слой, мы теперь вынуждены передавать именно такой размер батча (то есть в encoder и vae).

Функцией оптимизации возьмем Adam или RMSprop, обе показывают хорошие результаты.

from keras.optimizers import Adam, RMSprop

vae.compile(optimizer=Adam(start_lr), loss=vae_loss)

Код рисования рядов цифр и цифр из многообразия


Часто в процессе обучения модели требуется выполнять какие-то действия: изменять learning_rate, сохранять промежуточные результаты, сохранять модель, рисовать картинки и т.д.

Для этого в keras есть коллбэки, которые передаются в метод fit перед началом обучения. Например, чтобы влиять на learning rate в процессе обучения, есть такие коллбэки, как LearningRateScheduler, ReduceLROnPlateau, чтобы сохранять модель — ModelCheckpoint.

Отдельный коллбэк нужен для того, чтобы следить за процессом обучения в TensorBoard. Он автоматически будет добавлять в файл логов все метрики и лоссы, которые считаются между эпохами.

Для случая, когда требуется выполнение произвольных функций в процессе обучения, существует LambdaCallback. Он запускает выполнение произвольных функций в заданные моменты обучения, например, между эпохами или батчами.
Будем следить за процессом обучения, изучая, как генерируются цифры из .

from IPython.display import clear_output
from keras.callbacks import LambdaCallback, ReduceLROnPlateau, TensorBoard

# Массивы, в которые будем сохранять результаты, для последующей визуализации
figs = []
latent_distrs = []
epochs = []

# Эпохи, в которые будем сохранять
save_epochs = set(list((np.arange(0, 59)**1.701).astype(np.int)) + list(range(10)))

# Отслеживать будем на вот этих цифрах
imgs = x_test[:batch_size]
n_compare = 10

# Модели
generator      = models["decoder"]
encoder_mean   = models["z_meaner"]

# Функция, которую будем запускать после каждой эпохи
def on_epoch_end(epoch, logs):
    if epoch in save_epochs:
        clear_output() # Не захламляем output

        # Сравнение реальных и декодированных цифр
        decoded = vae.predict(imgs, batch_size=batch_size)
        plot_digits(imgs[:n_compare], decoded[:n_compare])

        # Рисование многообразия
        figure = draw_manifold(generator, show=True)

        # Сохранение многообразия и распределения z для создания анимации после
        epochs.append(epoch)
        figs.append(figure)
        latent_distrs.append(encoder_mean.predict(x_test, batch_size))
        
# Коллбэки
pltfig = LambdaCallback(on_epoch_end=on_epoch_end)
# lr_red = ReduceLROnPlateau(factor=0.1, patience=25)
tb     = TensorBoard(log_dir='./logs')

# Запуск обучения 
vae.fit(x_train, x_train, shuffle=True, epochs=1000,
        batch_size=batch_size,
        validation_data=(x_test, x_test),
        callbacks=[pltfig, tb],
        verbose=1)

Теперь, если установлен TensorBoard, можно следить за процессом обучения.

Вот как этот энкодер восстанавливает изображения:



А вот результат сэмплирования из



Вот так выглядит процесс обучения генерации цифр:


Распределение кодов в скрытом пространстве:


Не идеально нормальное, но довольно близко (особенно, учитывая, что размерность скрытого пространства всего 2).

Кривая обучения в TensorBoard



Видно, что размерности 2 для такой задачи очень мало, цифры очень размытые, а так же в промежутках между хорошими много рваных цифр.
В следующей части посмотрим, как генерировать цифры нужного лейбла, избавиться от рваных, а также как переносить стиль с одной цифры на другую.

Полезные ссылки и литература

Теоретическая часть основана на статье:
[1] Tutorial on Variational Autoencoders, Carl Doersch, 2016, https://arxiv.org/abs/1606.05908
и фактически является ее кратким изложением

Многие картинки взяты из блога Isaac Dykeman:
[2] Isaac Dykeman, http://ijdykeman.github.io/ml/2016/12/21/cvae.html

Подробнее прочитать про расстояние Кульбака-Лейблера на русском можно здесь:
[3] http://www.machinelearning.ru/wiki/images/d/d0/BMMO11_6.pdf

Код частично основан на статье Francois Chollet:
[4] https://blog.keras.io/building-autoencoders-in-keras.html

Другие интересные ссылки:
http://blog.fastforwardlabs.com/2016/08/12/introducing-variational-autoencoders-in-prose-and.html
http://kvfrans.com/variational-autoencoders-explained/