Уравнение теплопроводности в tensorflow / forpes.ru

Главная
Уравнение теплопроводности в tensorflow

Уравнение теплопроводности в tensorflow +32

13.02.2017 18:28

iphysic 8 6400 Источник

Привет, Хабр! Некоторое время назад увлекся глубоким обучением и стал потихоньку изучать tensorflow. Пока копался в tensorflow вспомнил про свою курсовую по параллельному программированию, которую делал в том году на 4 курсе университета. Задание там формулировалось так:

Линейная начально-краевая задача для двумерного уравнения теплопроводности:

$\frac{\partial u}{\partial t} = \sum \limits_{\alpha=1}^{2} \frac{\partial}{\partial x_\alpha} \left (k_\alpha \frac{\partial u}{\partial x_\alpha} \right ) -u, \quad x_\alpha \in [0,1] \quad (\alpha=1,2), \ t>0;$

$k_\alpha = \begin{cases} 50, (x_1, x_2) \in \Delta ABC\ 1, (x_1, x_2) \notin \Delta ABC \end{cases}$

$(\alpha = 1,2), \ A(0.2,0.5), \ B(0.7,0.2), \ C(0.5,0.8);$

$u(x_1, x_2, 0) = 0,\ u(0,x_2,t) = 1 - e^{-\omega t},\ u(1, x_2, t) = 0,$

$u(x_1,0,t) = 1 - e^{-\omega t},\ u(0, x_2, t) = 0,\ \omega = 20.$

Хотя правильнее было бы назвать это уравнением диффузии.

Задачу тогда требовалось решить методом конечных разностей по неявной схеме, используя MPI для распараллеливания и метод сопряженных градиентов.

Я не специалист в численных методах, пока не специалист в tensorflow, но опыт у меня уже появился. И я загорелся желанием попробовать вычислять урматы на фреймворке для глубокого обучения. Метод сопряженных градиентов реализовывать второй раз уже не интересно, зато интересно посмотреть как с вычислением справится tensorflow и какие сложности при этом возникнут. Этот пост про то, что из этого вышло.

Численный алгоритм

Определим сетку:

$\Omega = \omega_{x_1} \times \omega_{x_2} \times \omega_t,$

$\omega_{x_\alpha} = \left \{ x_{\alpha, i_\alpha} = i_\alpha h, i_\alpha = 0,...,N, h = \frac{1}{N}, \right \}\ \alpha = 1,2,$

$\[ \omega_t = \left \{t_j = j \tau, j=0,...,N_t, \tau = \frac{t_{max}}{N_t}\right \}.$

Разностная схема:

Чтобы проще было расписывать, введем операторы:

$\Delta_{1}f_{i,j} = \frac{f_{i+1/2,j} - f_{i-1/2,j}}{h},$

$\Delta_{2}f_{i,j} = \frac{f_{i,j+1/2} - f_{i,j-1/2}}{h}.$

Явная разностная схема:

$\frac{u_{i,j}^t - u_{i,j}^{t-1}}{\tau} = \Delta_{1}(k_{i,j}\Delta_{1}u_{i,j}^{t-1}) + \Delta_{2}(k_{i,j}\Delta_{2}u_{i,j}^{t-1}) - u_{i,j}^t.$

В случае явной разностной схемы для вычисления используются значения функции в предыдущий момент времени и не требуется решать уравнение на значения $u^t_{i,j}$ . Однако такая схема менее точная и требует значительно меньший шаг по времени.

Неявная разностная схема:

$\frac{u_{i,j}^t - u_{i,j}^{t-1}}{\tau} = \Delta_{1}(k_{i,j}\Delta_{1}u_{i,j}^t) + \Delta_{2}(k_{i,j}\Delta_{2}u_{i,j}^t) - u_{i,j}^t,$

$\frac{u_{i,j}^t - u_{i,j}^{t-1}}{\tau} = \Delta_{1}(k_{i,j}\frac{u_{i+1/2,j}^t - u_{i-1/2,j}^t}{h}) + \Delta_{2}(k_{i,j}\frac{u_{i,j+1/2}^t - u_{i,j-1/2}^t}{h}) - u_{i,j}^t,$

$\frac{u_{i,j}^t - u_{i,j}^{t-1}}{\tau} = \frac{k_{i+1/2,j}\frac{u_{i+1,j}^t - u_{i,j}^t}{h} - k_{i-1/2,j}\frac{u_{i,j}^t - u_{i-1/2,j}^t}{h}}{h} + \frac{k_{i,j+1/2}\frac{u_{i,j+1}^t - u_{i,j}^t}{h} - k_{i,j-1/2}\frac{u_{i,j}^t - u_{i,j-1/2}^t}{h}}{h} - u_{i,j}^t,$

$\frac{u_{i,j}^t - u_{i,j}^{t-1}}{\tau} = \frac{k_{i+1/2,j}u_{i+1,j}^t - u_{i,j}^t - k_{i-1/2,j}u_{i,j}^t - u_{i-1/2,j}^t + k_{i,j+1/2}u_{i,j+1}^t - u_{i,j}^t - k_{i,j-1/2}u_{i,j}^t - u_{i,j-1/2}^t}{h^2} - u_{i,j}^t.$

Перенесем в левую сторону все связанное с $u^t$ , а в правую $u^{t-1}$ и домножим на $\tau$ :

$(1 + \frac{\tau}{h^2}(k_{i+1/2,j} + k_{i-1/2,j} + k_{i,j+1/2} + k_{i,j-1/2}) + \tau)u_{i,j}^t - \\ - \frac{\tau}{h^2}(k_{i+1/2,j}u_{i+1,j}^t + k_{i-1/2,j}u^t_{i-1,j} + k_{i,j+1/2}u^t_{i,j+1} + k_{i,j-1/2}u^t_{i,j-1}) = u^{t-1}_{i,j}.$

По сути мы получили операторное уравнение над сеткой:

$Au^t = u^{t-1},$

что, если записать значения $u^t$ в узлах сетки как обычный вектор, является обычной системой линейных уравнений ( $Ax = b$ ). Значения в предыдущий момент времени константы, так как уже рассчитаны.
Для удобства представим оператор $A$ как разность двух операторов:

$A = D_A - (A^+ + A^{-}),$

где:

$D_A u^t = (1 + \frac{\tau}{h^2}(k_{i+1/2,j} + k_{i-1/2,j} + k_{i,j+1/2} + k_{i,j-1/2}) + \tau) u^t_{i,j},$

$(A^+ + A^{-})u^t = \frac{\tau}{h^2}(k_{i+1/2,j}u^t_{i+1,j} + k_{i-1/2,j}u^t_{i-1,j} + k_{i,j+1/2}u^t_{i,j+1} + k_{i,j-1/2}u^t_{i,j-1}).$

Заменив $u^t$ на нашу оценку $\hat{u}^t$ , запишем функционал ошибки:

$r = A\hat{u}^t - u^{t-1} = (D_A - A^+ - A^{-})\hat{u}^t - u^{t-1},$

$L = \sum r_{i,j}^2.$

где $r_{i,j}$ — ошибка в узлах сетки.

Будем итерационно минимизировать функционал ошибки, используя градиент.

В итоге задача свелась к перемножению тензоров и градиентному спуску, а это именно то, для чего tensorflow и был задуман.

Реализация на tensorflow

Кратко о tensorflow

В tensorflow сначала строится граф вычислений. Ресурсы под граф выделяются внутри tf.Session. Узлы графа — это операции над данными. Ячейками для входных данных в граф служат tf.placeholder. Чтобы выполнить граф, надо у объекта сессии запустить метод run, передав в него интересующую операцию и входные данные для плейсхолдеров. Метод run вернет результат выполнения операции, а также может изменить значения внутри tf.Variable в рамках сессии.

tensorflow сам умеет строить графы операций, реализующие backpropagation градиента, при условии, что в оригинальном графе присутствуют только операции, для которых реализован градиент (пока не у всех).

Код:

Сначала код инициализации. Здесь производим все предварительные операции и считаем все, что можно посчитать заранее.

Инициализация

# Импорты
import numpy as np
import pandas as pd
import tensorflow as tf
import matplotlib.pyplot as plt
import matplotlib
from matplotlib.animation import FuncAnimation
from matplotlib import cm
import seaborn


# Класс инкапсулирующий логику инициализации, выполнения и
# обучения графа уравнения теплопроводности
class HeatEquation():
    def __init__(self, nxy, tmax, nt, k, f, u0, u0yt, u1yt, ux0t, ux1t):
        self._nxy = nxy # точек в направлении x, y
        self._tmax = tmax # масимальное время
        self._nt = nt # количество моментов времени
        self._k  = k # функция k
        self._f  = f # функция f
        self._u0 = u0 # начальное условие
        # краевые условия
        self._u0yt = u0yt 
        self._u1yt = u1yt
        self._ux0t = ux0t
        self._ux1t = ux1t
        # шаги по координатам и по времени
        self._h  = h  = np.array(1./nxy)
        self._ht = ht = np.array(tmax/nt)
        print("ht/h/h:", ht/h/h)
	
        self._xs = xs = np.linspace(0., 1.,    nxy + 1)
        self._ys = ys = np.linspace(0., 1.,    nxy + 1)
        self._ts = ts = np.linspace(0., tmax,  nt  + 1) 
	
        from itertools import product
        # узлы сетки как векторы в пространстве
        self._vs  = vs  = np.array(list(product(xs, ys)), dtype=np.float64)
        # внутренние узлы
        self._vcs = vsc = np.array(list(product(xs[1:-1], ys[1:-1])), dtype=np.float64)
        
        # векторые в которых рассчитываются значения k
        vkxs = np.array(list(product((xs+h/2)[:-1], ys)), dtype=np.float64) # k_i+0.5,j
        vkys = np.array(list(product(xs, (ys+h/2)[:-1])), dtype=np.float64) # k_i    ,j+0.5
	
        # сетки со значениями k
        self._kxs = kxs = k(vkxs).reshape((nxy,nxy+1))
        self._kys = kys = k(vkys).reshape((nxy+1,nxy))
	
        # диагональный оператор D_A 
        D_A = np.zeros((nxy+1, nxy+1))
        D_A[0:nxy+1,0:nxy+0] += kys
        D_A[0:nxy+1,1:nxy+1] += kys
        D_A[0:nxy+0,0:nxy+1] += kxs
        D_A[1:nxy+1,0:nxy+1] += kxs
        self._D_A = D_A = 1 + ht/h/h*D_A[1:nxy,1:nxy] + ht
	
        # функция, которую будем искать
        self._U_shape = (nxy+1, nxy+1, nt+1)
        # выделяем сразу для всех точек и моментов времени,
        # очень много лишней памяти, но мне не жалко
        self._U = np.zeros(self._U_shape) 
   	# ее значение в нулевой момент времени
        self._U[:,:,0] = u0(vs).reshape(self._U_shape[:-1])

$\tau$ и $h$ следует брать такими, чтобы $\frac{\tau}{h^2}$ было небольшим, желательно, хотя бы < 1, особенно при использовании «негладких» функций.

Метод который строит граф уравнения:

Граф вычислений

# метод, строящий граф
    def build_graph(self, learning_rate):
        def reset_graph():
            if 'sess' in globals() and sess:
                sess.close()
            tf.reset_default_graph()
        
        reset_graph()

        nxy = self._nxy

        # входные параметры
        kxs_    = tf.placeholder_with_default(self._kxs, (nxy,nxy+1))
        kys_    = tf.placeholder_with_default(self._kys, (nxy+1,nxy))
        D_A_    = tf.placeholder_with_default(self._D_A, self._D_A.shape)
        U_prev_ = tf.placeholder(tf.float64, (nxy+1, nxy+1), name="U_t-1")
        f_      = tf.placeholder(tf.float64, (nxy-1, nxy-1), name="f")

        # значение функции в данный момент времени, его и будем искать
        U_ = tf.Variable(U_prev_, trainable=True, name="U_t", dtype=tf.float64)

        # срез тензора
        def s(tensor, frm):
            return tf.slice(tensor, frm, (nxy-1, nxy-1))

        # вычисления действия оператора A+_A- на u
        Ap_Am_U_  = s(U_, (0, 1))*s(self._kxs, (0, 1))
        Ap_Am_U_ += s(U_, (2, 1))*s(self._kxs, (1, 1))
        Ap_Am_U_ += s(U_, (1, 0))*s(self._kys, (1, 0))
        Ap_Am_U_ += s(U_, (1, 2))*s(self._kys, (1, 1))
        Ap_Am_U_ *= self._ht/self._h/self._h

        # остатки
        res = D_A_*s(U_,(1, 1)) - Ap_Am_U_ - s(U_prev_, (1, 1)) - self._ht*f_

        # функционал ошибки, который будет оптимизироваться
        loss = tf.reduce_sum(tf.square(res), name="loss_res")

        # краевые условия и их влияния на функцию потерь
        u0yt_ = None
        u1yt_ = None
        ux0t_ = None
        ux1t_ = None
        if self._u0yt:        
            u0yt_ = tf.placeholder(tf.float64, (nxy+1,), name="u0yt")
            loss += tf.reduce_sum(tf.square(tf.slice(U_, (0, 0),   (1, nxy+1))
                    - tf.reshape(u0yt_, (1, nxy+1))), name="loss_u0yt")
        if self._u1yt:
            u1yt_ = tf.placeholder(tf.float64, (nxy+1,), name="u1yt")
            loss += tf.reduce_sum(tf.square(tf.slice(U_, (nxy, 0), (1, nxy+1))
                    - tf.reshape(u1yt_, (1, nxy+1))), name="loss_u1yt")
        if self._ux0t:
            ux0t_ = tf.placeholder(tf.float64, (nxy+1,), name="ux0t")
            loss += tf.reduce_sum(tf.square(tf.slice(U_, (0, 0),   (nxy+1, 1))
                    - tf.reshape(ux0t_, (nxy+1, 1))), name="loss_ux0t")
        if self._ux1t:
            ux1t_ = tf.placeholder(tf.float64, (nxy+1,), name="ux1t")
            loss += tf.reduce_sum(tf.square(tf.slice(U_, (0, nxy), (nxy+1, 1))
                    - tf.reshape(ux1t_, (nxy+1, 1))), name="loss_ux1t")
        # на удивление, у операции присвоения значения отдельным элементам в тензоре, 
        # на момент написания, нет реализованного градиента
        
        loss /= (nxy+1)*(nxy+1)

        # шаг оптимизации функционала 
        train_step = tf.train.AdamOptimizer(learning_rate, 0.7, 0.97).minimize(loss)

        # возврат в словаре операций графа, которые будем запускать
        self.g = dict(
            U_prev = U_prev_,
            f = f_,
            u0yt = u0yt_,
            u1yt = u1yt_,
            ux0t = ux0t_,
            ux1t = ux1t_,
            U = U_,
            res = res,
            loss = loss,
            train_step = train_step
        )
        return self.g

По-хорошему надо было считать значения функции на краях заданными и оптимизировать значения функции только во внутренней области, но с этим возникли проблемы. Способа сделать оптимизируемым только часть тензора не нашлось, и у операции присвоения значения срезу тензора не написан градиент (на момент написания поста). Можно было бы попробовать хитро повозиться на краях или написать свой оптимизатор. Но и просто добавление разности на краях значений функции и краевых условий в функционал ошибки хорошо работает.

Стоит отметить, что метод с адаптивным моментом показал себя наилучшим образом, пусть функционал ошибки и квадратичный.

Вычисление функции: в каждый момент времени делаем несколько оптимизационных итераций, пока не превысим maxiter или ошибка не станет меньше eps, сохраняем и переходим к следующему моменту.

Вычисление

def train_graph(self, eps, maxiter, miniter):
        g = self.g
        losses = []
        # запускам контекст сессии
        with tf.Session() as sess:
            # инициализируем место под данные в графе
            sess.run(tf.global_variables_initializer(), feed_dict=self._get_graph_feed(0))
            for t_i, t in enumerate(self._ts[1:]):
                t_i += 1
                losses_t = []
                losses.append(losses_t)
                d = self._get_graph_feed(t_i)
                p_loss = float("inf")
                for i in range(maxiter):
                    # запускаем граф итерации оптимизации
                    # и получаем значения u, функционала потерь 
                    _, self._U[:,:,t_i], loss = sess.run([g["train_step"], g["U"], g["loss"]], feed_dict=d)
                    losses_t.append(loss)
                    if i > miniter and abs(p_loss - loss) < eps:
                        p_loss = loss
                        break
                    p_loss = loss
                print('#', end="")
        return self._U, losses

Запуск:

Код запуска

tmax = 0.5
nxy  = 100
nt   = 10000

A = np.array([0.2, 0.5])
B = np.array([0.7, 0.2])
C = np.array([0.5, 0.8])

k1 = 1.0
k2 = 50.0
omega = 20

# проверка принадлежности точки треугольнику
def triang(v, k1, k2, A, B, C):
    v_ = v.copy()
    k = k1*np.ones([v.shape[0]])
    v_ = v - A
    B_ = B - A
    C_ = C - A
    m = (v_[:, 0]*B_[1] - v_[:, 1]*B_[0]) / (C_[0]*B_[1] - C_[1]*B_[0])
    l = (v_[:, 0] - m*C_[0]) / B_[0]
    inside = (m > 0.) * (l > 0.) * (m + l < 1.0)
    k[inside] = k2
    return k

# 0.0
def f(v, t):
    return 0*triang(v, h0, h1, A, B, C)

# 0.0
def u0(v):
    return 0*triang(v, t1, t2, A, B, C)

# краевые условия
def u0ytb(t, ys):
    return 1 - np.exp(-omega*np.ones(ys.shape[0])*t)

def ux0tb(t, xs):
    return 1 - np.exp(-omega*np.ones(xs.shape[0])*t)

def u1ytb(t, ys):
    return 0.*np.ones(ys.shape[0])

def ux1tb(t, xs):
    return 0.*np.ones(xs.shape[0])

# запуск и получение результата
eq = HeatEquation(nxy, tmax, nt, lambda x: triang(x, k1, k2, A, B, C), f, u0, u0ytb, u1ytb, ux0tb, ux1tb)
_ = eq.build_graph(0.001)
U, losses = eq.train_graph(1e-6, 100, 1)

Результаты

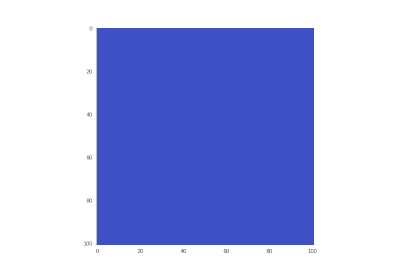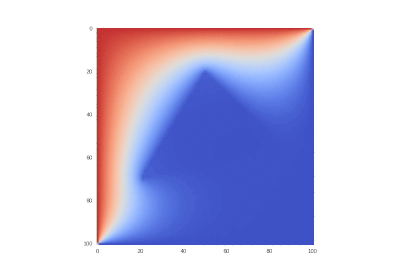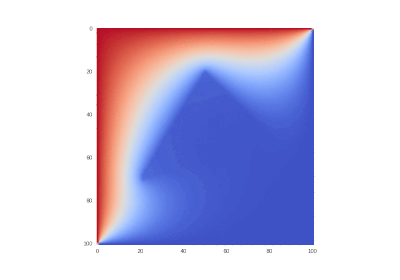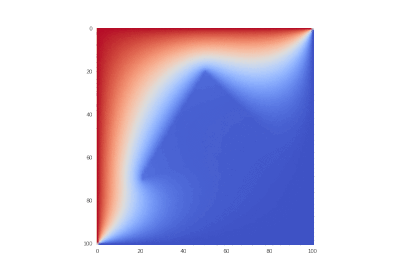
Оригинальное условие:

Скрытый текст

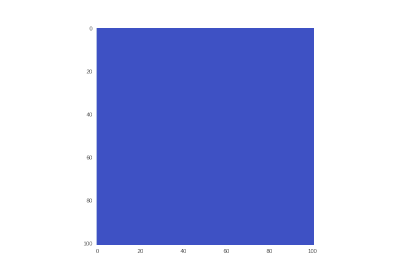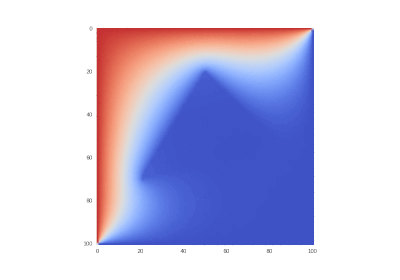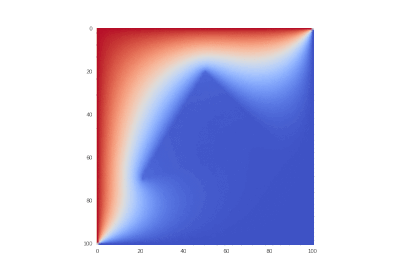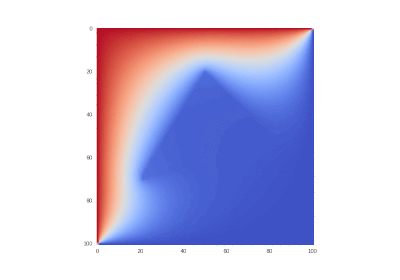
Условие как и оригинальное, но без $-u$ в уравнении:

Скрытый текст

$\frac{\partial u}{\partial t} = \sum \limits_{\alpha=1}^{2} \frac{\partial}{\partial x_\alpha} \left (k_\alpha \frac{\partial u}{\partial x_\alpha} \right ), \quad x_\alpha \in [0,1] \quad (\alpha=1,2), \ t>0;$

$k_\alpha = \begin{cases} 50, (x_1, x_2) \in \Delta ABC\ 1, (x_1, x_2) \notin \Delta ABC \end{cases}$

$u(x_1, x_2, 0) = 0,\ u(0,x_2,t) = 1 - e^{-\omega t},\ u(1, x_2, t) = 0,$

$u(x_1,0,t) = 1 - e^{-\omega t},\ u(0, x_2, t) = 0,\ \omega = 20.$

Что легко правится в коде:

# в методе __init__
self._D_A = D_A = 1 + ht/h/h*D_A[1:nxy,1:nxy]

Разницы почти нет, потому что производные имеют большие порядки, чем сама функция.

Далее везде:

$\frac{\partial u}{\partial t} = \sum \limits_{\alpha=1}^{2} \frac{\partial}{\partial x_\alpha} \left (k_\alpha \frac{\partial u}{\partial x_\alpha} \right ) +f, \quad x_\alpha \in [0,1] \quad (\alpha=1,2), \ t>0;$

Условие с одним нагревающимся краем:

Скрытый текст

$k_\alpha = \begin{cases} 10, (x_1, x_2) \in \Delta ABC\ 1, (x_1, x_2) \notin \Delta ABC \end{cases}$

$f(x_1,x_2,t) = 0,$

$u(x_1, x_2, 0) = 0,\ u(0,x_2,t) = 1 - e^{-\omega t},\ u(1, x_2, t) = 0,$

$u(x_1,0,t) = 0,\ u(0, x_2, t) = 0,\ \omega = 20.$

Условие с остыванием изначально нагретой области:

Скрытый текст

$k_\alpha = 1,$

$f(x_1,x_2,t) = 0,$

$u(x_1, x_2, 0) = \begin{cases} 0.1, (x_1, x_2) \in \Delta ABC\ 0, (x_1, x_2) \notin \Delta ABC \end{cases}$

$u(0,x_2,t) = 0,\ u(1, x_2, t) = 0,$

$u(x_1,0,t) = 0,\ u(0, x_2, t) = 0.$

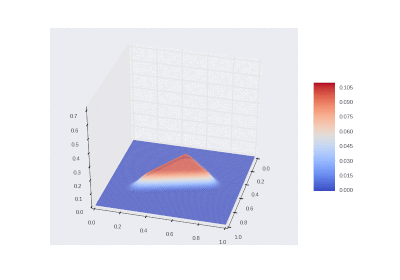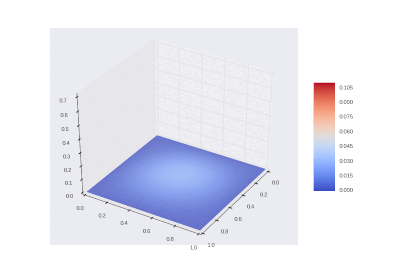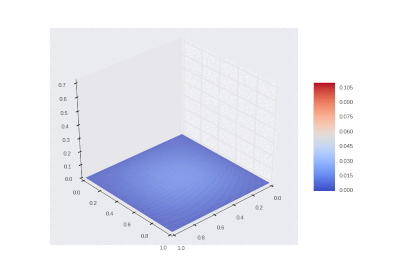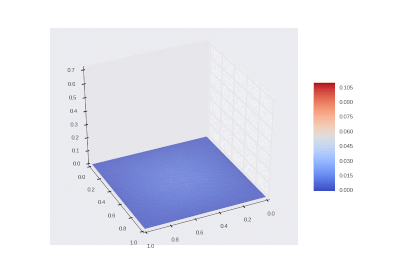
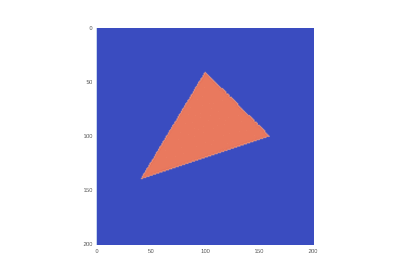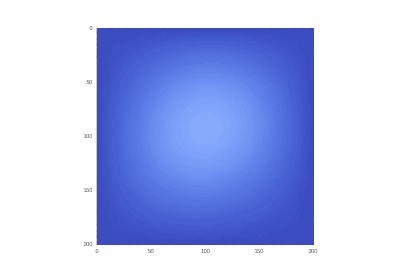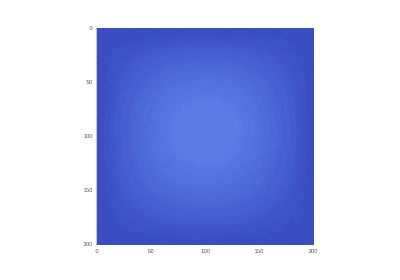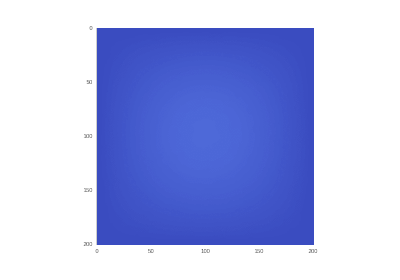
Условие с включением нагрева в области:

Скрытый текст

$k_\alpha = \begin{cases} 2, (x_1, x_2) \in \Delta ABC\ 10, (x_1, x_2) \notin \Delta ABC \end{cases}$

$f(x_1,x_2,t) = \begin{cases} 10, (x_1, x_2) \in \Delta ABC\ 0, (x_1, x_2) \notin \Delta ABC \end{cases}$

$u(x_1, x_2, 0) = 0,\ u(0,x_2,t) = 0,\ u(1, x_2, t) = 0,$

$u(x_1,0,t) = 0,\ u(0, x_2, t) = 0.$

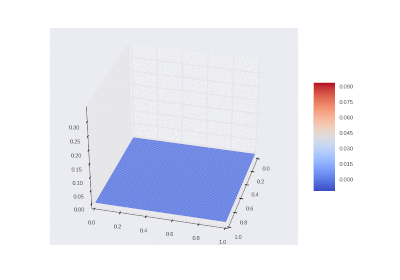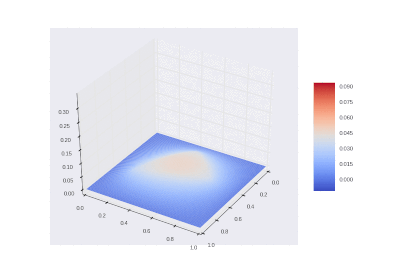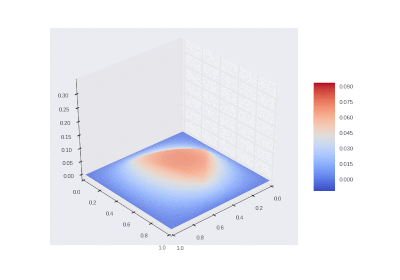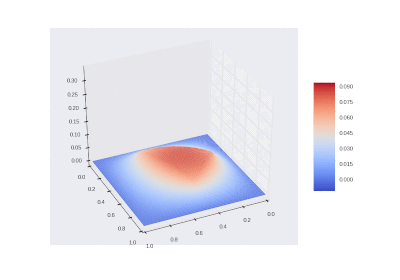
Рисование гифок

Функция рисования 3D-гифки:

3d gif

В основной класс добавляем метод, возвращающий U в виде pandas.DataFrame

def get_U_as_df(self, step=1):
        nxyp  = self._nxy + 1
        nxyp2 = nxyp**2
        Uf = self._U.reshape((nxy+1)**2,-1)[:, ::step]
        data = np.hstack((self._vs, Uf))
        df = pd.DataFrame(data, columns=["x","y"] + list(range(len(self._ts))[0::step]))
        return df

def make_gif(Udf, fname):
    from mpl_toolkits.mplot3d import Axes3D
    from matplotlib.ticker import LinearLocator, FormatStrFormatter
    from scipy.interpolate import griddata
    
    fig = plt.figure(figsize=(10,7))

    ts = list(Udf.columns[2:])
    data = Udf

    # преобразуем сетку в данные, которые умеет рисовать matplotlib
    x1 = np.linspace(data['x'].min(), data['x'].max(), len(data['x'].unique()))
    y1 = np.linspace(data['y'].min(), data['y'].max(), len(data['y'].unique()))
    x2, y2 = np.meshgrid(x1, y1)
    z2s = list(map(lambda x: griddata((data['x'], data['y']), data[x], (x2, y2), 
    method='cubic'), ts))

    zmax = np.max(np.max(data.iloc[:, 2:])) + 0.01
    zmin = np.min(np.min(data.iloc[:, 2:])) - 0.01

    plt.grid(True)
    ax = fig.gca(projection='3d')
    ax.view_init(35, 15)
    ax.set_zlim(zmin, zmax)
    ax.zaxis.set_major_locator(LinearLocator(10))
    ax.zaxis.set_major_formatter(FormatStrFormatter('%.02f'))

    norm = matplotlib.colors.Normalize(vmin=zmin, vmax=zmax, clip=False)
    surf = ax.plot_surface(x2, y2, z2s[0], rstride=1, cstride=1, norm=norm, cmap=cm.coolwarm, linewidth=0., antialiased=True)
    fig.colorbar(surf, shrink=0.5, aspect=5)

    # функция перерисовки картинки в новом кадре
    def update(t_i):
        label = 'timestep {0}'.format(t_i)
        ax.clear()
        print(label)
        surf = ax.plot_surface(x2, y2, z2s[t_i], rstride=1, cstride=1, norm=norm, cmap=cm.coolwarm, linewidth=0., antialiased=True)
        ax.view_init(35, 15+0.5*t_i)
        ax.set_zlim(zmin, zmax)
        return surf,
    # создание и сохранение анимации
    anim = FuncAnimation(fig, update, frames=range(len(z2s)), interval=50)
    anim.save(fname, dpi=80, writer='imagemagick')

Функция рисования 2D-гифки:

2d gif

def make_2d_gif(U, fname, step=1):
    fig = plt.figure(figsize=(10,7))

    zmax = np.max(np.max(U)) + 0.01
    zmin = np.min(np.min(U)) - 0.01
    norm = matplotlib.colors.Normalize(vmin=zmin, vmax=zmax, clip=False)
    im=plt.imshow(U[:,:,0], interpolation='bilinear', cmap=cm.coolwarm, norm=norm)
    plt.grid(False)
    nst = U.shape[2] // step

    # функция перерисовки картинки в новом кадре
    def update(i):
        im.set_array(U[:,:,i*step])
        return im
    # создание и сохранение анимации
    anim = FuncAnimation(fig, update, frames=range(nst), interval=50)
    anim.save(fname, dpi=80, writer='imagemagick')

Итог

Стоит отметить, что оригинальное условие без использования GPU считалось 4м 26с, а с использованием GPU 2м 11с. При больших значениях точек разрыв растет. Однако не все операции в полученном графе GPU-совместимы.

Характеристики машины:

Intel Core i7 6700HQ 2600 МГц,
NVIDIA GeForce GTX 960M.

Посмотреть, какие операции на чем выполняются, можно с помощью следующего кода:

Скрытый текст

# В основном классе
    def check_metadata_partitions_graph(self):
        g = self.g
        d = self._get_graph_feed(1)
        with tf.Session() as sess:
            sess.run(tf.global_variables_initializer(), feed_dict=d)
            options = tf.RunOptions(output_partition_graphs=True)
            metadata = tf.RunMetadata()
            c_val = sess.run(g["train_step"], feed_dict=d, options=options, 
            				 run_metadata=metadata)
        print(metadata.partition_graphs)

Это был интересный опыт. Tensorflow неплохо показал себя для этой задачи. Может быть даже такой подход получит какое-то применение — всяко приятнее писать код на питоне, чем на C/C++, а с развитием tensorflow станет еще проще.

Спасибо за внимание!

Использованная литература

— Бахвалов Н. С., Жидков Н. П., Г. М. Кобельков Численные методы, 2011

Поделиться с друзьями

-->

Комментарии (8)

QtRoS
13.02.2017 23:08
#10068512
Кто знает, может быть TF приобретет популярность и в этой сфере. Кто же знал, например, что видеокарточки так зарешают в машинном обучении :)

3aicheg
14.02.2017 03:34
#10068736
+1
вычислять урматы

Урматы — это вид шкрабов?
1. hudson
  14.02.2017 09:25
  #10068918
  +2
  Уравнения математической физики, коротко — урматы )

nikolay_karelin
14.02.2017 11:18
#10069188
Интересная идея!

Несколько вопросов:

1) Если ли репозиторий с материалами статьи? Или лучше всего прямо отсюда примеры кода брать

2) Оценивали ли вы, какая часть вычислений идет на GPU? Я правильно понял, что у вас только 100 точек по х (где можно параллельно считать) и 10000 по t, где вычисления сугубо последовательные? Даже в этом случае 2 раза ускорение — это круто.

3) Пробовали ли вы сравнивать производительность TensorFlow с компилацией в Cython?
1. iphysic
  14.02.2017 12:24
  #10069362
  Добрый день!
  
  1) Ноутбук Jupyter: http://nbviewer.jupyter.org/github/urtrial/pde/blob/master/partial_differential_equation.ipynb
  
  2) Почти, 101 точек по x и 101 по y, то есть 10 201 точек по координатам и 10 000 по времени (конкретно для того примера). Да, смотрел, примерно половина операций в графе идут на GPU, какие именно не помню, но думаю, что самые основные вроде перемножения или сложения тензоров.
  
  3) C Cython'ом не сравнивал, но время работы сравнимо и даже быстрее моей реализации на С + MPI для курсовой (у меня правда нет уверенности в оптимальности того кода).

gbg
14.02.2017 13:46
#10069550
Сделайте классический тест — 101x101 точку, и потом 201x201 точку.
порядок аппроксимации у вашей схемы — второй, поэтому если будет разбежка раньше, чем в 4 знаке после запятой — решатель можно отправлять на доработку.
1. Uranix
  14.02.2017 17:23
  #10070210
  Там разрывный коэффициент теплопроводности. Второй порядок получить нетривиально (я знаю как это сделать только для 1D уравнения)

nikolay_karelin
14.02.2017 21:54
#10070878
Кстати, если кого заинтересует, аналогичный пример, но уже от авторов TensorFlow: https://www.tensorflow.org/tutorials/pdes/