Содержание
- Часть 1: Введение
- Часть 2: Manifold learning и скрытые (latent) переменные
- Часть 3: Вариационные автоэнкодеры (VAE)
- Часть 4: Conditional VAE
- Часть 5: GAN (Generative Adversarial Networks) и tensorflow
- Часть 6: VAE + GAN
В прошлой части мы познакомились с вариационными автоэнкодерами (VAE), реализовали такой на keras, а также поняли, как с его помощью генерировать изображения. Получившаяся модель, однако, обладала некоторыми недостатками:
- Не все цифры получилось хорошо закодировать в скрытом пространстве: некоторые цифры либо вообще отсутствовали, либо были очень смазанными. В промежутках между областями, в которых были сконцентрированы варианты одной и той же цифры, находились вообще какие-то бессмысленные иероглифы.
Что тут писать, вот так выглядели сгенерированные цифры:
Картинка
- Сложно было генерировать картинку какой-то заданной цифры. Для этого надо было смотреть, в какую область латентного пространства попадали изображения конкретной цифры, и сэмплить уже откуда-то оттуда, а тем более было сложно генерировать цифру в каком-то заданном стиле.
В этой части мы посмотрим, как можно лишь совсем немного усложнив модель преодолеть обе эти проблемы, и заодно получим возможность генерировать картинки новых цифр в стиле другой цифры – это, наверное, самая интересная фича будущей модели.
Сначала подумаем о причинах 1-го недостатка:
Многообразия, на которых лежат различные цифры, могут быть далеко друг от друга в пространстве картинок. То есть сложно представить, как, например, непрерывно отобразить картинку цифры „5“, в картинку цифры „7“, при том, чтобы все промежуточные картинки можно было назвать правдоподобными. Таким образом, многообразие, около которого лежат цифры, вовсе не обязано быть линейно связанным. Автоэнкодер же, в силу того что является композицией непрерывных функций, сам может отображать в код и обратно только непрерывно, особенно если это вариационный автоэнкодер. В нашем предыдущем примере все усложнялось еще и тем, что автоэнкодер пытался искать двумерное многообразие.
В качестве иллюстрации вернемся к нашему искусственному примеру из 2-ой части, только сделаем определяющее многообразие несвязным:
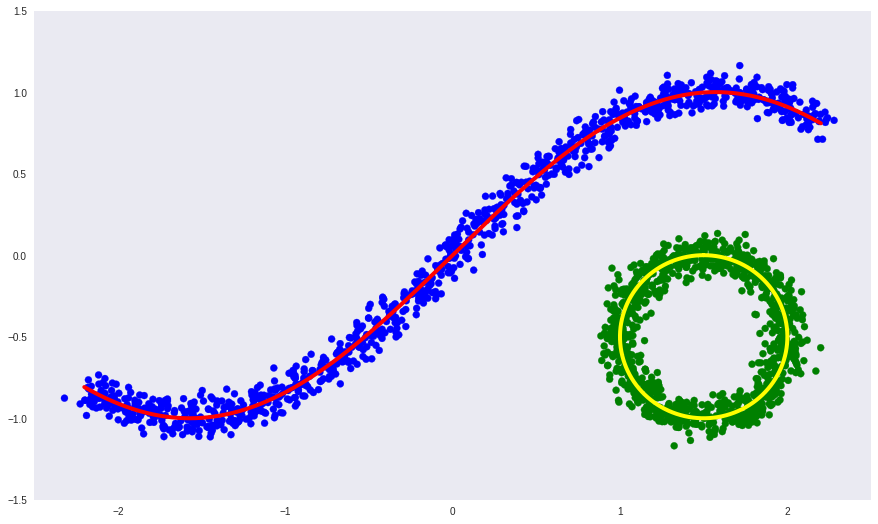
Здесь:
- синие и зеленые точки — объекты выборки,
- красная и желтая кривые — несвязанное определяющее многообразие.
Попробуем теперь выучить определяющее многообразие с помощью обычного глубокого автоэнкодера.
# Импорт необходимых библиотек
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
# Создание датасета
x1 = np.linspace(-2.2, 2.2, 1000)
fx = np.sin(x1)
dots1 = np.vstack([x1, fx]).T
t = np.linspace(0, 2*np.pi, num=1000)
dots2 = 0.5*np.array([np.sin(t), np.cos(t)]).T + np.array([1.5, -0.5])[None, :]
dots = np.vstack([dots1, dots2])
noise = 0.06 * np.random.randn(*dots.shape)
labels = np.array([0]*1000 + [1]*1000)
noised = dots + noise
# Визуализация
colors = ['b']*1000 + ['g']*1000
plt.figure(figsize=(15, 9))
plt.xlim([-2.5, 2.5])
plt.ylim([-1.5, 1.5])
plt.scatter(noised[:, 0], noised[:, 1], c=colors)
plt.plot(dots1[:, 0], dots1[:, 1], color="red", linewidth=4)
plt.plot(dots2[:, 0], dots2[:, 1], color="yellow", linewidth=4)
plt.grid(False)
# Модель и обучение
from keras.layers import Input, Dense
from keras.models import Model
from keras.optimizers import Adam
def deep_ae():
input_dots = Input((2,))
x = Dense(64, activation='elu')(input_dots)
x = Dense(64, activation='elu')(x)
code = Dense(1, activation='linear')(x)
x = Dense(64, activation='elu')(code)
x = Dense(64, activation='elu')(x)
out = Dense(2, activation='linear')(x)
ae = Model(input_dots, out)
return ae
dae = deep_ae()
dae.compile(Adam(0.001), 'mse')
dae.fit(noised, noised, epochs=300, batch_size=30, verbose=2)
# Результат
predicted = dae.predict(noised)
# Визуализация
plt.figure(figsize=(15, 9))
plt.xlim([-2.5, 2.5])
plt.ylim([-1.5, 1.5])
plt.scatter(noised[:, 0], noised[:, 1], c=colors)
plt.plot(dots1[:, 0], dots1[:, 1], color="red", linewidth=4)
plt.plot(dots2[:, 0], dots2[:, 1], color="yellow", linewidth=4)
plt.scatter(predicted[:, 0], predicted[:, 1], c='white', s=50)
plt.grid(False)
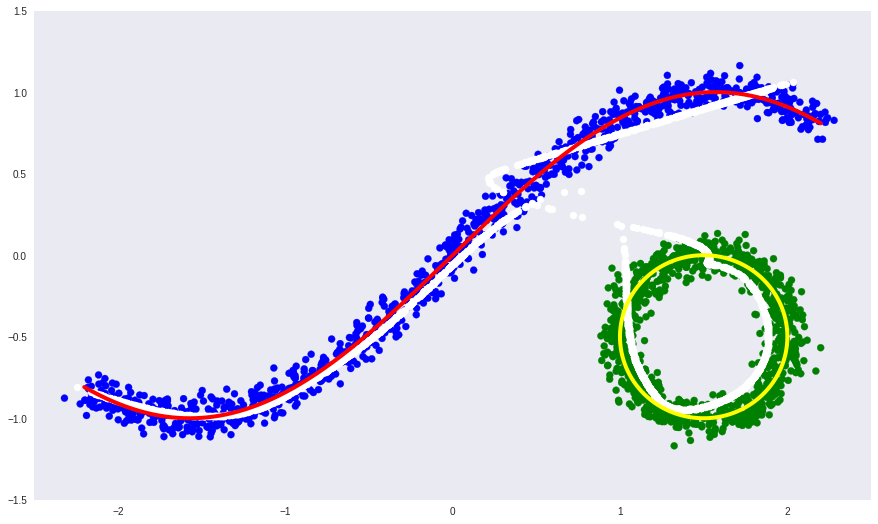
- белая линия — многообразие в которое переходят синие и зеленые точки данных после автоэнкодера, то есть попытка автоэнкодера построить многообразие, определяющее больше всего вариации в данных.
Видно, что у простого автоэнкодера не получилось выучить форму несвязного многообразия. Вместо этого он хитро продолжил одно в другое.
Если же мы знаем лейблы данных, которые определяют на каком из частей несвязного многообразия лежат эти данные (как с цифрами), то мы можем просто condition автоэнкодер на этих лейблах. То есть просто дополнительно с данными подавать на вход энкодеру и декодеру еще и лейблы данных. В таком случае источником разрывности в данных будет лейбл, и это позволит автоэнкодеру выучить каждую часть линейно несвязного многообразия отдельно.
Посмотрим на тот же самый пример, только теперь на вход и энкодеру, и декодеру будем передавать дополнительно еще и лейбл.
from keras.layers import concatenate
def deep_cond_ae():
input_dots = Input((2,))
input_lbls = Input((1,))
full_input = concatenate([input_dots, input_lbls])
x = Dense(64, activation='elu')(full_input)
x = Dense(64, activation='elu')(x)
code = Dense(1, activation='linear')(x)
full_code = concatenate([code, input_lbls])
x = Dense(64, activation='elu')(full_code)
x = Dense(64, activation='elu')(x)
out = Dense(2, activation='linear')(x)
ae = Model([input_dots, input_lbls], out)
return ae
cdae = deep_cond_ae()
cdae.compile(Adam(0.001), 'mse')
cdae.fit([noised, labels], noised, epochs=300, batch_size=30, verbose=2)
predicted = cdae.predict([noised, labels])
# Визуализация
plt.figure(figsize=(15, 9))
plt.xlim([-2.5, 2.5])
plt.ylim([-1.5, 1.5])
plt.scatter(noised[:, 0], noised[:, 1], c=colors)
plt.plot(dots1[:, 0], dots1[:, 1], color="red", linewidth=4)
plt.plot(dots2[:, 0], dots2[:, 1], color="yellow", linewidth=4)
plt.scatter(predicted[:, 0], predicted[:, 1], c='white', s=50)
plt.grid(False)
На этот раз автоэнкодеру удалось выучить линейно несвязное определяющее многообразие.
CVAE
Если же теперь взять VAE, как в предыдущей части, и подавать на вход еще и лейблы, то получится Conditional Variational Autoencoder (CVAE).
С картинками цифр получается вот так:
Картинка выше из [2]
В этом случае основное уравнение VAE из прошлой части становится просто conditioned на
( не обязан быть дискретным), то есть на лейбле.![\log P(X|Y;\theta_2) - KL[Q(Z|X,Y;\theta_1)||P(Z|X,Y;\theta_2)] = E_{Z \sim Q}[\log P(X|Z,Y;\theta_2)] - KL[Q(Z|X,Y;\theta_1)||N(0,I)]](https://habrastorage.org/getpro/habr/post_images/2a6/61b/69e/2a661b69ea2aa2351f7493a41469c789.svg)
мы опять сравниваем с 
.Это можно интерпретировать так: для каждого
у нас отдельный автоэнкодер VAE, при этом у них огромное количество общих весов (почти абсолютный weight sharing).В результате получается, что CVAE кодирует в
свойства входного сигнала общие для всех .Перенос стиля
(Комментарий: это не то же самое, что перенос стиля в Prisme, там совсем другое)
Теперь становится понятно, как создавать новые картинки в стиле заданной:
- обучаем CVAE на картинках с лейблами,
- кодируем стиль заданной картинки в ,
- меняя лейблы , создаем из закодированного новые картинки.
Код на Keras
Код практически идентичен коду из предыдущей части, за исключением того, что теперь в энкодер и декодер передается и лейбл цифры.
import sys
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# import seaborn as sns
from keras.datasets import mnist
from keras.utils import to_categorical
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test .astype('float32') / 255.
x_train = np.reshape(x_train, (len(x_train), 28, 28, 1))
x_test = np.reshape(x_test, (len(x_test), 28, 28, 1))
y_train_cat = to_categorical(y_train).astype(np.float32)
y_test_cat = to_categorical(y_test).astype(np.float32)
num_classes = y_test_cat.shape[1]
batch_size = 500
latent_dim = 8
dropout_rate = 0.3
start_lr = 0.001
from keras.layers import Input, Dense
from keras.layers import BatchNormalization, Dropout, Flatten, Reshape, Lambda
from keras.layers import concatenate
from keras.models import Model
from keras.objectives import binary_crossentropy
from keras.layers.advanced_activations import LeakyReLU
from keras import backend as K
def create_cvae():
models = {}
# Добавим Dropout и BatchNormalization
def apply_bn_and_dropout(x):
return Dropout(dropout_rate)(BatchNormalization()(x))
# Энкодер
input_img = Input(shape=(28, 28, 1))
flatten_img = Flatten()(input_img)
input_lbl = Input(shape=(num_classes,), dtype='float32')
x = concatenate([flatten_img, input_lbl])
x = Dense(256, activation='relu')(x)
x = apply_bn_and_dropout(x)
# Предсказываем параметры распределений
# Вместо того чтобы предсказывать стандартное отклонение, предсказываем логарифм вариации
z_mean = Dense(latent_dim)(x)
z_log_var = Dense(latent_dim)(x)
# Сэмплирование из Q с трюком репараметризации
def sampling(args):
z_mean, z_log_var = args
epsilon = K.random_normal(shape=(batch_size, latent_dim), mean=0., stddev=1.0)
return z_mean + K.exp(z_log_var / 2) * epsilon
l = Lambda(sampling, output_shape=(latent_dim,))([z_mean, z_log_var])
models["encoder"] = Model([input_img, input_lbl], l, 'Encoder')
models["z_meaner"] = Model([input_img, input_lbl], z_mean, 'Enc_z_mean')
models["z_lvarer"] = Model([input_img, input_lbl], z_log_var, 'Enc_z_log_var')
# Декодер
z = Input(shape=(latent_dim, ))
input_lbl_d = Input(shape=(num_classes,), dtype='float32')
x = concatenate([z, input_lbl_d])
x = Dense(256)(x)
x = LeakyReLU()(x)
x = apply_bn_and_dropout(x)
x = Dense(28*28, activation='sigmoid')(x)
decoded = Reshape((28, 28, 1))(x)
models["decoder"] = Model([z, input_lbl_d], decoded, name='Decoder')
models["cvae"] = Model([input_img, input_lbl, input_lbl_d],
models["decoder"]([models["encoder"]([input_img, input_lbl]), input_lbl_d]),
name="CVAE")
models["style_t"] = Model([input_img, input_lbl, input_lbl_d],
models["decoder"]([models["z_meaner"]([input_img, input_lbl]), input_lbl_d]),
name="style_transfer")
def vae_loss(x, decoded):
x = K.reshape(x, shape=(batch_size, 28*28))
decoded = K.reshape(decoded, shape=(batch_size, 28*28))
xent_loss = 28*28*binary_crossentropy(x, decoded)
kl_loss = -0.5 * K.sum(1 + z_log_var - K.square(z_mean) - K.exp(z_log_var), axis=-1)
return (xent_loss + kl_loss)/2/28/28
return models, vae_loss
models, vae_loss = create_cvae()
cvae = models["cvae"]
from keras.optimizers import Adam, RMSprop
cvae.compile(optimizer=Adam(start_lr), loss=vae_loss)
digit_size = 28
def plot_digits(*args, invert_colors=False):
args = [x.squeeze() for x in args]
n = min([x.shape[0] for x in args])
figure = np.zeros((digit_size * len(args), digit_size * n))
for i in range(n):
for j in range(len(args)):
figure[j * digit_size: (j + 1) * digit_size,
i * digit_size: (i + 1) * digit_size] = args[j][i].squeeze()
if invert_colors:
figure = 1-figure
plt.figure(figsize=(2*n, 2*len(args)))
plt.imshow(figure, cmap='Greys_r')
plt.grid(False)
ax = plt.gca()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()
n = 15 # Картинка с 15x15 цифр
from scipy.stats import norm
# Так как сэмплируем из N(0, I), то сетку узлов, в которых генерируем цифры, берем из обратной функции распределения
grid_x = norm.ppf(np.linspace(0.05, 0.95, n))
grid_y = norm.ppf(np.linspace(0.05, 0.95, n))
def draw_manifold(generator, lbl, show=True):
# Рисование цифр из многообразия
figure = np.zeros((digit_size * n, digit_size * n))
input_lbl = np.zeros((1, 10))
input_lbl[0, lbl] = 1
for i, yi in enumerate(grid_x):
for j, xi in enumerate(grid_y):
z_sample = np.zeros((1, latent_dim))
z_sample[:, :2] = np.array([[xi, yi]])
x_decoded = generator.predict([z_sample, input_lbl])
digit = x_decoded[0].squeeze()
figure[i * digit_size: (i + 1) * digit_size,
j * digit_size: (j + 1) * digit_size] = digit
if show:
# Визуализация
plt.figure(figsize=(10, 10))
plt.imshow(figure, cmap='Greys_r')
plt.grid(False)
ax = plt.gca()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()
return figure
def draw_z_distr(z_predicted, lbl):
# Рисование рпспределения z
input_lbl = np.zeros((1, 10))
input_lbl[0, lbl] = 1
im = plt.scatter(z_predicted[:, 0], z_predicted[:, 1])
im.axes.set_xlim(-5, 5)
im.axes.set_ylim(-5, 5)
plt.show()
from IPython.display import clear_output
from keras.callbacks import LambdaCallback, ReduceLROnPlateau, TensorBoard
# Массивы, в которые будем сохранять результаты для последующей визуализации
figs = [[] for x in range(num_classes)]
latent_distrs = [[] for x in range(num_classes)]
epochs = []
# Эпохи, в которые будем сохранять
save_epochs = set(list((np.arange(0, 59)**1.701).astype(np.int)) + list(range(10)))
# Отслеживать будем на вот этих цифрах
imgs = x_test[:batch_size]
imgs_lbls = y_test_cat[:batch_size]
n_compare = 10
# Модели
generator = models["decoder"]
encoder_mean = models["z_meaner"]
# Функция, которую будем запускать после каждой эпохи
def on_epoch_end(epoch, logs):
if epoch in save_epochs:
clear_output() # Не захламляем output
# Сравнение реальных и декодированных цифр
decoded = cvae.predict([imgs, imgs_lbls, imgs_lbls], batch_size=batch_size)
plot_digits(imgs[:n_compare], decoded[:n_compare])
# Рисование многообразия для рандомного y и распределения z|y
draw_lbl = np.random.randint(0, num_classes)
print(draw_lbl)
for lbl in range(num_classes):
figs[lbl].append(draw_manifold(generator, lbl, show=lbl==draw_lbl))
idxs = y_test == lbl
z_predicted = encoder_mean.predict([x_test[idxs], y_test_cat[idxs]], batch_size)
latent_distrs[lbl].append(z_predicted)
if lbl==draw_lbl:
draw_z_distr(z_predicted, lbl)
epochs.append(epoch)
# Коллбэки
pltfig = LambdaCallback(on_epoch_end=on_epoch_end)
# lr_red = ReduceLROnPlateau(factor=0.1, patience=25)
tb = TensorBoard(log_dir='./logs')
# Запуск обучения
cvae.fit([x_train, y_train_cat, y_train_cat], x_train, shuffle=True, epochs=1000,
batch_size=batch_size,
validation_data=([x_test, y_test_cat, y_test_cat], x_test),
callbacks=[pltfig, tb],
verbose=1)
Результаты
(Извиняюсь, что местами белые цифры на черном фоне, а местами черные на белом)
Переводит цифры этот автоэнкодер вот так:
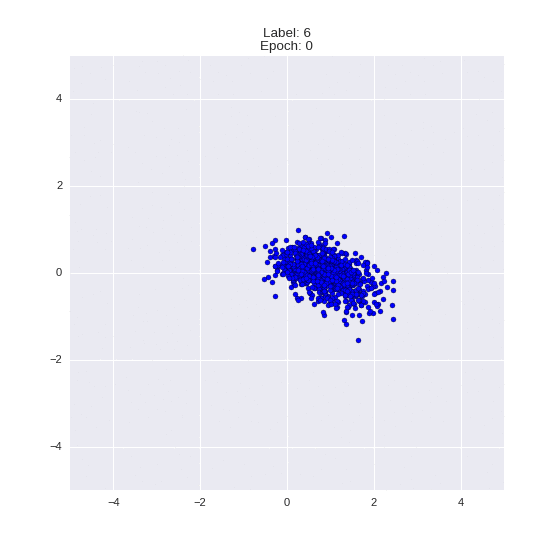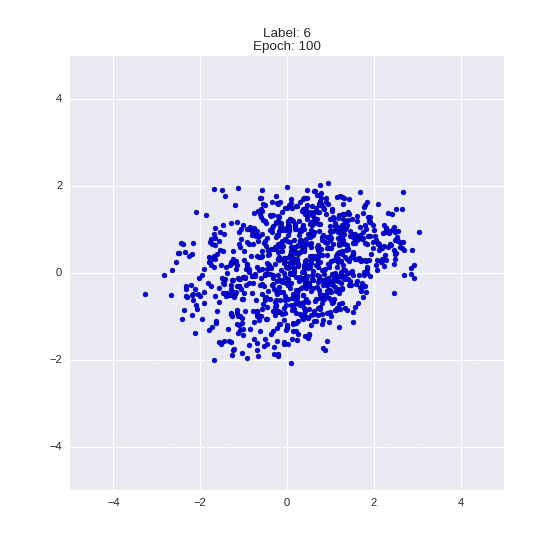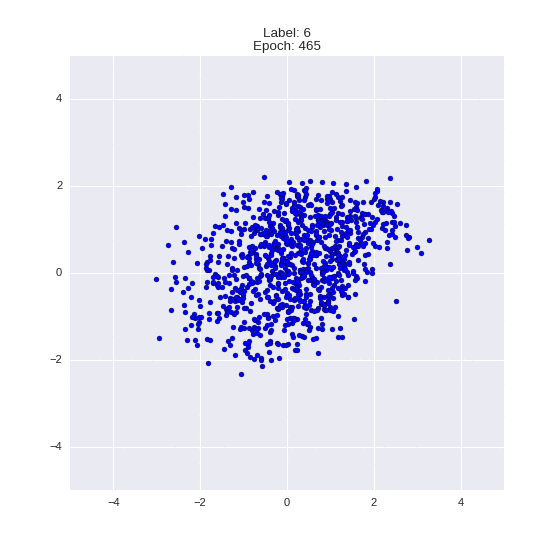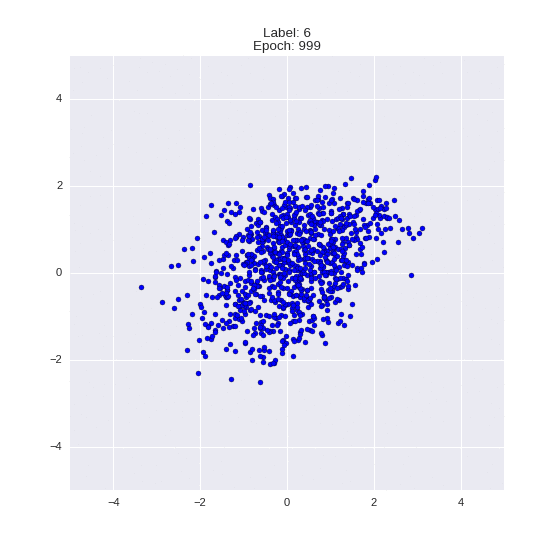
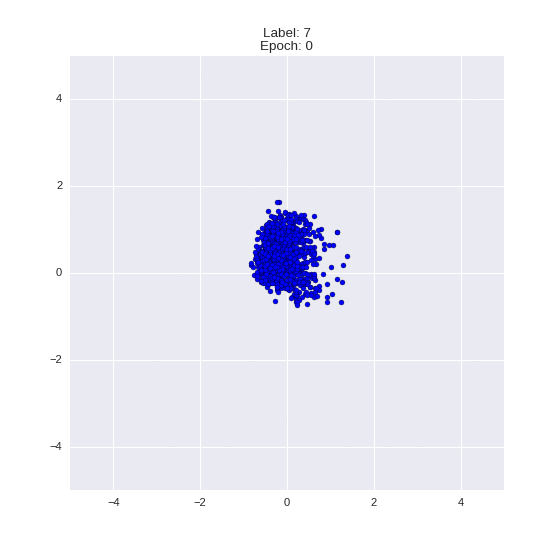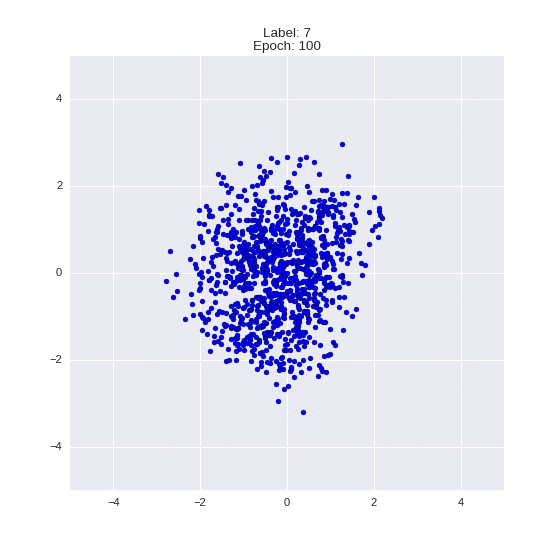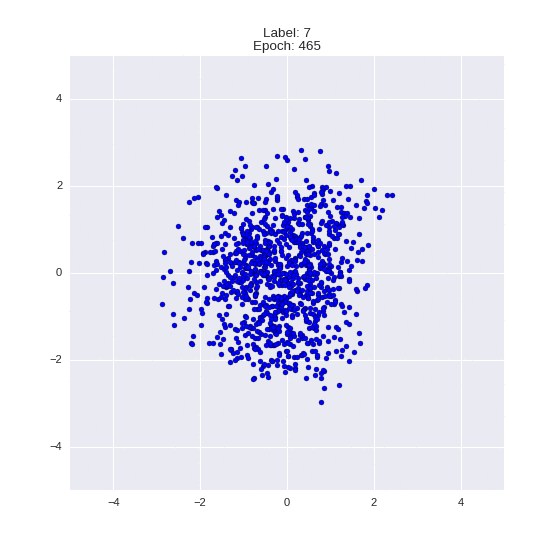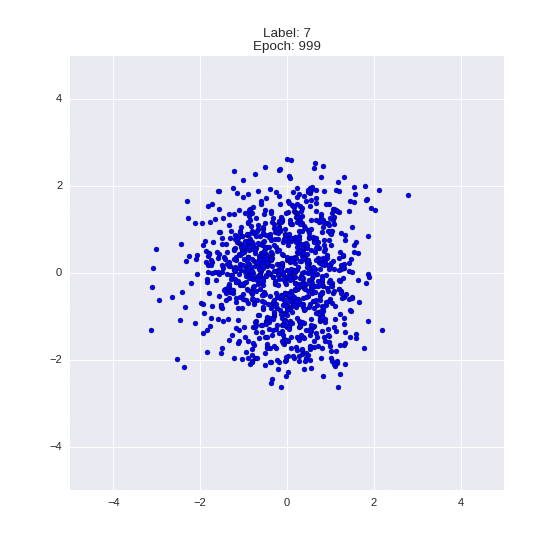
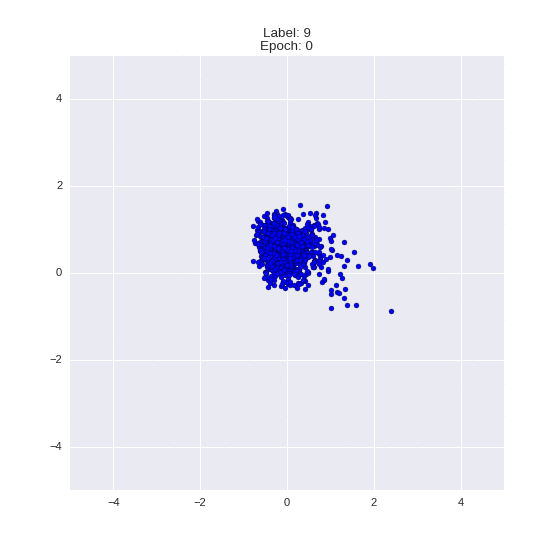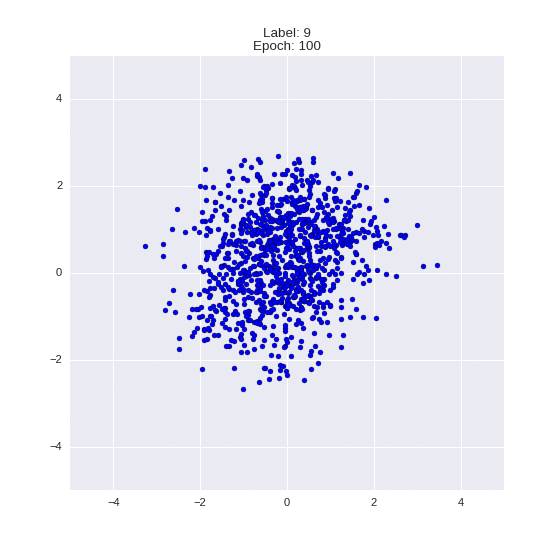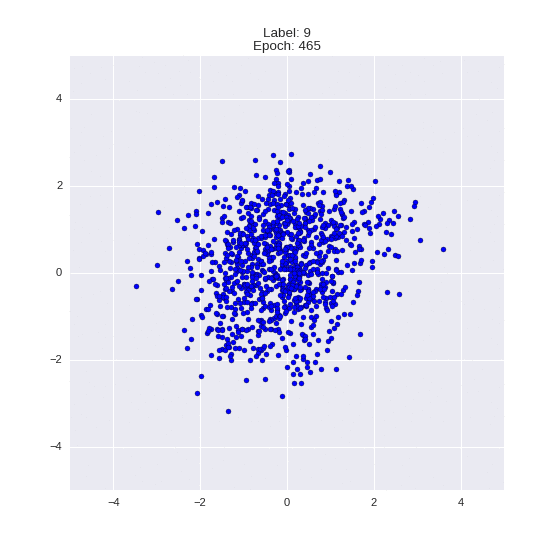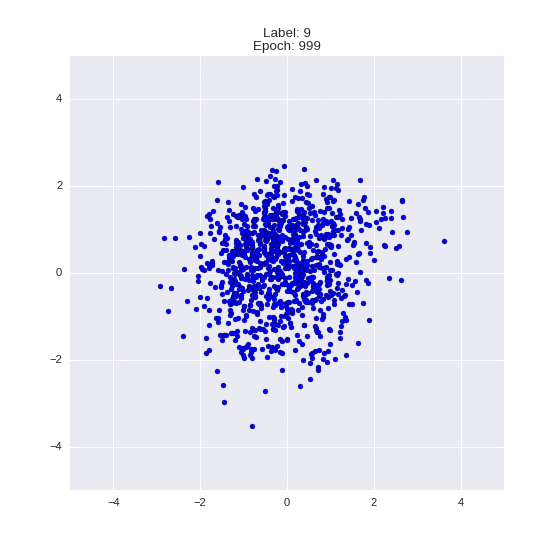
Сгенерированные цифры каждого лейбла сэмплированные из
:(Отлично видно как общие черты закодированы в координатах
)
Генерация цифр заданного лейбла из и распределение для каждого лейбла
Перенос стиля этой моделью
В качестве источников стиля возьмем первые десять «7»-ок, и на основе их кода
создадим остальные цифры.def style_transfer(model, X, lbl_in, lbl_out):
rows = X.shape[0]
if isinstance(lbl_in, int):
lbl = lbl_in
lbl_in = np.zeros((rows, 10))
lbl_in[:, lbl] = 1
if isinstance(lbl_out, int):
lbl = lbl_out
lbl_out = np.zeros((rows, 10))
lbl_out[:, lbl] = 1
return model.predict([X, lbl_in, lbl_out])
n = 10
lbl = 7
generated = []
prot = x_train[y_train == lbl][:n]
for i in range(num_classes):
generated.append(style_transfer(models["style_t"], prot, lbl, i))
generated[lbl] = prot
plot_digits(*generated, invert_colors=True)
Стиль перенесен довольно удачно: сохранены наклон и толщина штриха.
Больше свойств стиля можно было бы переносить, просто увеличив размерность
, это также сделало бы цифры менее размытыми.В следующей части посмотрим, как, используя генеративные состязающиеся сети (GAN), генерировать цифры практически неотличимые от настоящих, а после этого и как объединить GAN'ы с автоэнкодерами.
Код создания гифок
from matplotlib.animation import FuncAnimation
from matplotlib import cm
import matplotlib
def make_2d_figs_gif(figs, epochs, c, fname, fig):
norm = matplotlib.colors.Normalize(vmin=0, vmax=1, clip=False)
im = plt.imshow(np.zeros((28,28)), cmap='Greys', norm=norm)
plt.grid(None)
plt.title("Label: {}\nEpoch: {}".format(c, epochs[0]))
def update(i):
im.set_array(figs[i])
im.axes.set_title("Label: {}\nEpoch: {}".format(c, epochs[i]))
im.axes.get_xaxis().set_visible(False)
im.axes.get_yaxis().set_visible(False)
return im
anim = FuncAnimation(fig, update, frames=range(len(figs)), interval=100)
anim.save(fname, dpi=80, writer='imagemagick')
def make_2d_scatter_gif(zs, epochs, c, fname, fig):
im = plt.scatter(zs[0][:, 0], zs[0][:, 1])
plt.title("Label: {}\nEpoch: {}".format(c, epochs[0]))
def update(i):
fig.clear()
im = plt.scatter(zs[i][:, 0], zs[i][:, 1])
im.axes.set_title("Label: {}\nEpoch: {}".format(c, epochs[i]))
im.axes.set_xlim(-5, 5)
im.axes.set_ylim(-5, 5)
return im
anim = FuncAnimation(fig, update, frames=range(len(zs)), interval=100)
anim.save(fname, dpi=80, writer='imagemagick')
for lbl in range(num_classes):
make_2d_figs_gif(figs[lbl], epochs, lbl, "./figs4/manifold_{}.gif".format(lbl), plt.figure(figsize=(7,7)))
make_2d_scatter_gif(latent_distrs[lbl], epochs, lbl, "./figs4/z_distr_{}.gif".format(lbl), plt.figure(figsize=(7,7)))
Полезные ссылки и литература
Теоретическая часть основана на статье:
[1] Tutorial on Variational Autoencoders, Carl Doersch, https://arxiv.org/abs/1606.05908
и фактически является ее кратким изложением.
Многие картинки взяты из блога Isaac Dykeman:
[2] Isaac Dykeman, http://ijdykeman.github.io/ml/2016/12/21/cvae.html
Подробнее прочитать про расстояние Кульбака-Лейблера на русском можно в
[3] http://www.machinelearning.ru/wiki/images/d/d0/BMMO11_6.pdf
Код частично основан на статье Francois Chollet:
[4] https://blog.keras.io/building-autoencoders-in-keras.html
Другие интересные ссылки:
http://blog.fastforwardlabs.com/2016/08/12/introducing-variational-autoencoders-in-prose-and.html
http://kvfrans.com/variational-autoencoders-explained/
Комментарии (12)
supersonic_snail
26.06.2017 17:26Зачем у вас дропаут вообще есть? Он оказывает какое-то положительное влияние на значение negative-log-likelihood на тестсете? По моему опыту VAE обучается с трудом и недообучение гораздо большая проблема, чем перееобучение. Какая-то еще регуляризация только ухудшает результат.
Результат с тем, что AE не справился с волна+круг, я немного неосилил — вы даете ему код размером 1, это маловато. Естественно он не может разделить эти две вещи. А что если дать код размером 100? Разве что вы намекаете, что код должен быть достаточно большой и даже тысячи может не хватить для реальных данных.
Можете немного раскрыть интригу — про что вы будете говорить в VAE+GAN? Избавляться от размытостей или от KL divergenc-а?
Вообще, статьи очень хорошие, спасибо что пишете.iphysic
26.06.2017 18:29По поводу дропаута: ну сам по себе он нужен не только для регуляризации, он еще и вынуждает активации в слоях быть более-менее независимыми, например, чтобы одни активация не исправляли другие, а также чтобы следующий слой не слишком полагался на активации конкретных нейронов ниже. Так поидее слои выучиваются более равномерно и больше нелинейностей используется. Я бы сказал, что тут больше претензия к батч-нормализации: по последним данным она куда лучше работает перед активацией, а не после (опять же из-за этого больше нелинейностей в слое появляется).
По поводу одномерности кода: во второй статье было про то, что автоэнкодер выучивает k-мерное определяющее многообразие, где k — размерность кода. В данном случае определяющее многообразие искусственно одномерное, поэтому и код одномерный, больше было бы уже переобучение. На том примере показывается именно то, что в случае без лейблов автоэнкодер вынужден продолжать одну связную область в другую, а в случае, когда есть лейблы он может выучить их по-отдельности.
Могу раскрыть. В VAE + GAN буду избавлять именно от размытостей.
Спасибо!
supersonic_snail
26.06.2017 19:15Ну да, все верно, дропаут влияет на то, как сеть что-то там внутри делает, как и batchnorm, но в конце концов это всего лишь средства направленные на получить циферку метрики пониже да побыстрее. Если этого не видно, ты выглядит как дропаут ради дропаута. Ну да ладно, это придирки.
Я бы не сказал, что код размером >1 это оверфит. Скорее код размером 1 — андерфит. Оверфит был бы если бы вы дали мало точек на кривой и оно бы построило по ним что-нибудь вроде полинома высокого порядка. Тут такого нет — тут вообще кусок полностью прямой.
GAN можно использовать чтобы изящно уйти от KL и от сэмплинга из диагонального гауссиана при обучении. Это неплохо бы вписалось в ваши 6 статей.
PS — виноват, ответил в корень.erwins22
26.06.2017 19:41+1«код размером >1» -тут имеется ввиду вектор сжатия из задачи «волна и круг»?
«KL»? сложно искать в гугле такие короткие термины.
Заранее спасибо за расшифровку.
И еще почему просто не использовать метод главных компонент для батча на слое перед сжатием?
Он по идеи приведет к независимости компонент.supersonic_snail
26.06.2017 19:51Код это я имею в виду то, во что сжимает автоенкодер по ходу обработки информации, code в вашем исходнике. И да, в волна-круг задаче.
KL — KL divergence. Он же используется чтобы сделать так, чтобы q(z|x) примерно походил на p(z), но из-за невычислимости приходится делать предположение, что q(z|x) — диагональный гауссиан, а p(z) — стандартный гауссиан. Тогда можно посчитать аналитически. GAN позволяет оба ограничения убрать, то есть произвольный q(z|x) и произвольный p(z). Найти можно тут, но статья довольно суровая для неподготовленного читателя.
Насчет метода главных компонент я не совсем понял, где его вы предлагаете вставлять. Как этакий продвинутый batchnorm?erwins22
26.06.2017 20:04в принципе да.
Собираю данные батча, Применяя метод главных компонент, корректирующий веса следующего слоя.
Далее умножается на скорректированный слой.
Если сходиться, то мы получаем автоматом максимально разделенные компоненты без всякой возни с vaesupersonic_snail
26.06.2017 22:16Если делать так, то нужно каждую итерацию пересчитывать главные компоненты. Это О(n^3), где n — размер извлекаемых фич, что жутко медленно. batchnorm это O(n).
iphysic
26.06.2017 20:27По поводу дропоута, возможно лосс на тесте он бы и не уменьшил, не проверял, если честно. Но во всех статьях, что видел, его используют, так что я просто даже не пробовал его убирать)
А вот по поводу кодов не могу согласиться, когда входная размерность 2, то при размерности кодов, скажем, 100, автоэнкодер бы без проблем выучил тождественную функцию и толку бы от него не было (там же не вае, регуляризации на код никакой нету). Даже при двух это теоритически возможно)
За статью огромное спасибо, прочитаю в ближайшее время!supersonic_snail
26.06.2017 22:14Да, вы правы, я понял. Если код сильно большой, то оно просто скопирует вход, поэтому делаем denoising ae и так далее.
erwins22
почему Conditional?
supersonic_snail
Обычный VAE моделирует p(x) — вероятность данных. Если добавить то, что там за цифра должна быть — становится p(x|y), где для каждого x дано y. Такое в литературе принято называть conditional. y может быть не только то, что за цифра: раскраска черно-белой картинки — это тоже conditional. Только x — цветные картинки, y — черно-белые.