
Учёные исследуют Вселенную и видят удивительную структуру. В ней встречаются фантастически сложные объекты и процессы. Каждое событие во Вселенной следует точным законам природы, идеально выражаемым на языке математики. Эти законы кажутся нам точно подстроенными для того, чтобы смогла появиться жизнь, и, в частности, – разумная жизнь. Каковы эти законы природы и как нам их найти?
Вселенная так хорошо структурирована и упорядочена, что мы сравниваем её с самыми сложными и точными изобретениями своего времени. В XVIII и XIX веках Вселенную сравнивали с идеально работающими часами. Философы тогда обсуждали Часовщика. В XX и XXI веке самый сложный объект – компьютер. Вселенную сравнивают с идеально работающим суперкомпьютером. Исследователи задаются вопросом: как этот компьютер запрограммировали?
Как можно объяснить всю эту структуру? Почему законы кажутся идеально настроенными на появление жизни, и почему они выражаются таким точным математическим языком? На самом ли деле Вселенная так структурирована, как кажется?

Один из ответов на эти вопросы – платонизм (или его кузен, реализм). Это вера в то, что законы природы объективны и всегда существовали. Они обладают точной и идеальной формой, существующей в мире Платона. Эти законы идеально работают, и они сформировали Вселенную, которую мы наблюдаем. Они не только существуют в этом мире, но и живут рядом с идеальной математикой. Это должно помочь объяснить, почему законы пишутся на языке математики.
Платонизм оставляет желать лучшего, причём много. Основная проблема платонизма – это метафизика, а не наука. Но даже если мы примем его, всё равно останется множество вопросов. Почему в платоническом мире есть законы, порождающие разумную жизнь во Вселенной, а не какие-то другие? Как вообще появился этот платонический чердак? Почему физическая Вселенная следует эфемерным правилам? Как учёным и математикам получить доступ в сундук Платона с сокровищами в виде точных идеалов?
Мультивселенная – другой ответ, в последнее время ставший весьма модным. Эта теория – попытка объяснить, почему в нашей Вселенной есть законы, дающие жизнь. Верящий в Мультивселенную утверждает, что наша вселенная – лишь одна из многих. У каждой вселенной есть свой набор правил и свои возможные структуры, им соответствующие. Физики, продвигающие теорию мультивселенной, считают, что законы в каждой вселенной складываются случайно. В нашей Вселенной мы видим пригодные для жизни структуры потому, что нам повезло жить в одной из немногих вселенных, в которых есть такие законы. И хотя Мультивселенная объясняет некоторые видимые нами структуры, некоторые вопросы остаются открытыми. Вместо того, чтобы спрашивать, почему у Вселенной есть такие структуры, мы можем спросить, почему у Мультивселенной есть такие структуры. Ещё одна проблема: если Мультивселенная и ответит на некоторые наши вопросы, то кто сказал, что она существует? Поскольку большинство верит, что с другими вселенными у нас нет никакой связи, то вопрос существования Мультивселенной остаётся в области метафизики.
Есть ещё одно, более интересное, объяснение структуры законов природы. Вместо того, чтобы говорить, что Вселенная очень структурирована, скажите, что Вселенная хаотична, и по большей части в ней нет структуры. А причина, по которой мы видим структуры, в том, что учёные работают, как сито; они фокусируются только на тех явлениях, у которых есть структура и которые можно предсказать. Они не рассматривают все явления. Вместо этого они выбирают только те, с которыми могут управиться.
Некоторые люди скажут, что наука изучает все физические явления. Это не так. Кто выиграет следующие выборы президента США и переедет в Белый дом – это физический вопрос, но ни один учёный не станет искать точный ответ на него. Остановит компьютер работу или нет при определённых входных данных – вопрос вроде бы физический, и всё же от Алана Тьюринга мы узнаём, что ответить на него нельзя. Учёные дали классификацию общим текстурам и высотам различных типов облаков, но в целом совсем не интересуются точной формой облака. Хотя его форма – явление физическое, учёные даже не пытаются его изучать. Наука не изучает все явления. Наука изучает предсказуемые физические явления. Это почти тавтология: наука предсказывает предсказуемые явления.
Учёные описали критерий для явлений, которые они решили изучать: он называется симметрией. Симметрия – это свойство, согласно которому, несмотря на изменение чего-то, остаётся какая-то неизменная часть. Когда мы говорим, что у лица есть симметрия, мы имеем в виду, что если отразить левую часть и заменить её правой, оно будет выглядеть так же. Когда физики используют слово «симметрия», они обсуждают наборы физических явлений. У набора явлений есть симметрия, если после некоторого изменения он остаётся таким же. Самый очевидный пример — симметрия местоположения. Это значит, что если провести тот же самый эксперимент в двух разных местах, результаты должны быть одинаковыми. Симметрия времени означает, что результаты экспериментов не должны зависеть от того, когда эксперимент проводился. Есть множество других типов симметрии.
У явлений, избранных учёными для исследований, должно быть множество разных типов симметрий. Когда физик видит много явлений, он сначала должен определить, есть ли у них симметрия. Он проводит эксперименты в разных местах и в разное время. Если он достигает тех же результатов, он затем изучает их в поисках первопричины. Если же эксперименты оказались несимметричными, он их игнорирует.
И хотя такие учёные, как Галилей и Ньютон видели симметрию в физических явлениях, вся мощь симметрии впервые была исследована Альбертом Эйнштейном. Он заявил, что законы физики должны оставаться теми же самыми, даже если экспериментатор двигается со скоростью, близкой к скорости света. Памятуя об этой симметрии, он смог создать законы специальной теории относительности. Эйнштейн первым понял, что симметрия служит определяющей характеристикой физики. У чего есть симметрия, у того будет закон природы. А остальное не принадлежит к науке.
Вскоре после того, как Эйнштейн показал жизненную важность симметрии для науки, Эмми Нётер доказала мощную теорему, определившую связь между симметрией и законами сохранения. Она связана с константами природы, центральной частью современной физики. Опять-таки, при наличии симметрии будут и законы сохранения, и константы. Физик должен быть ситом, и изучать явления, обладающие симметрией, позволяя тем явлениям, что симметрией не обладают, проскальзывать сквозь пальцы.
С этим объяснением существующих во Вселенной структур есть несколько проблем. Например, кажется, что выбираемые нами явления, обладающие законами природы, порождают все остальные явления. У всех законов физики частиц, гравитации и квантовой теории есть симметрии, и все они изучаются физиками. Кажется, что все явления происходят из этих теорий, даже те, что симметрией не обладают. Так что, хотя определение следующего президента США не входит в задачи науки, это явление будет определено социологией, которая определена психологией, которая определена нейробиологией, которая зависит от химии, которая зависит от физики частиц и квантовой механики. Определить победителя выборов слишком сложно для учёных, но результаты выборов зависят от законов физики, являющихся частью науки.
Несмотря на то, что у нас не получилось объяснить структуру законов природы, мы считаем, что это – наилучший кандидат на решение. Это одно из тех решений, что не включают каких бы то ни было метафизических принципов или существования множества невидимых вселенных. Нам не нужно выглядывать за пределы Вселенной в поисках причины структуры, находящейся внутри её. Нам нужно только взглянуть на то, как мы рассматриваем явления.
Перед тем, как мы продолжим, необходимо указать, что у нашего решения есть свойство, общее с решением, связанным с Мультивселенной. Мы постулировали, что по большей части Вселенная хаотична и в ней нет особой структуры. Просто мы фокусируемся на небольшом количестве существующих структур. Точно так же тот, кто верит в Мультивселенную, считает, что у большей её части не достаёт структуры для формирования разумной жизни. Только в малом количестве избранных вселенных можно найти сложные структуры. И мы, население этой сложной Вселенной, фокусируемся на этих редких структурах. Оба решения заключаются в концентрации на небольшом объёме структуры, являющейся частью огромного хаотичного целого.
Иерархия числовых систем
Идея о том, что мы видим структуру только потому, что избираем подмножество явлений, нова и сложна для восприятия. В математике есть аналогичная ситуация, которую гораздо проще понять. Мы сконцентрируемся на одном важном примере, в котором чётко виден процесс селекции. Сначала нам нужно совершить небольшую экскурсию по нескольким числовым системам и их свойствам.
Рассмотрим вещественные числа. В одном из старших классов школы учитель рисует линию вещественных чисел на доске и утверждает, что на ней есть все числа, которые вам когда-либо понадобятся. Если взять два вещественных числа, мы сможем их складывать, вычитать, перемножать и делить. Из них состоит числовая система, используемая во всех аспектах науки. У вещественных чисел есть одно важное свойство: они упорядочены. из двух любых разных вещественных чисел одно будет больше другого. Представьте числовую линию: из двух разных точек одна будет правее другой. Это свойство настолько очевидно, что о нём редко говорят.

Эмми Нётер
И хотя вещественные числа кажутся законченной картиной, история на них не заканчивается. Уже в XVI столетии математики начали поиски более сложных числовых систем. Они начали работать с «мнимым» числом i, свойство которого такого, что его квадрат равен -1. Это явно контрастирует с любым вещественным числом, чей квадрат всегда положителен. Мнимое число они определили как произведение вещественного числа и i. Математики определили комплексное число как сумму вещественного и мнимого. Если r1 и r2 — вещественные числа, тогда r1+r2i – комплексное число. Поскольку комплексное число состоит из двух вещественных, мы рисуем их на двумерной плоскости. Прямая вещественных чисел находится на комплексной плоскости. Это соответствует тому факту, что каждое вещественное число r1 можно рассматривать как комплексное r1+0i (само число плюс нулевое комплексное слагаемое).
Мы знаем, как складывать, вычитать, перемножать и делить комплексные числа. Однако у них есть одно необычное свойство. В отличие от вещественных, комплексные числа не упорядочены. Какое из двух комплексных чисел, допустим 3 + 7.2i и 6 — 4i, больше, а какое – меньше? Очевидного ответа нет. В принципе, конечно, комплексные числа можно упорядочить, но это упорядочивание не будет соответствовать их перемножению). То, что комплексные числа не упорядочены, означает, что мы теряем структуру при переходе от вещественных к комплексным числам.
Но история не заканчивается на комплексных числах. Точно так же, как из пар вещественных можно составить комплексные числа, из пар комплексных можно составить кватернионы. Пусть c1 = r1 + r2i и c2 = r3 + r4i будут комплексными числами. Тогда можно определить кватернион как q = c1 + c2j, где j – особое число. Оказывается, что любой кватернион можно записать в виде
r1 + r2i + r3j + r4k
где i, j и k – особые числа, схожие с комплексными (ijk = -1 = i2 = j2 = k2). Так что если комплексные числа состоят из двух вещественных, то кватернионы состоят из четырёх вещественных чисел. Каждое комплексное число r1 + r2i можно рассматривать как особый тип кватерниона: r1+ r2i + 0j + 0k. Мы можем представить себе кватернионы как четырёхмерное пространство, двумерным подмножеством которого являются комплексные числа. Нам, людям, довольно сложно визуализировать пространства высокого порядка.
Кватернионы – полноправная числовая система. Их легко можно складывать, вычитать, умножать и делить. Как и комплексные числа, их нельзя упорядочить. И у них ещё меньше структуры, чем у комплексных чисел. Если умножение комплексных чисел коммутативно, то есть, для любых комплексных чисел c1 и c2 верно c1c2 = c2c1, это верно не для всех кватернионов. Это значит, что существуют кватернионы q1 и q2 такие, что q1q2 не равно q2q1.
Этот процесс удвоения числовой системы при помощи нового особого числа называется процедурой Кэли-Диксона в честь математиков Артура Кэли и Леонарда Диксона. Для числовой системы определённого типа можно построить другую числовую систему с размерностью вдвое больше изначальной. Новая система получается хуже структурированной (у неё есть меньше аксиом), чем изначальная.
Применив процедуру Кэли-Диксона к кватернионам, мы получим числовую систему октонионов. Это восьмимерная числовая система. Это значит, что каждый из окнтоионов можно записать через восемь вещественных чисел, как
r1+ r2i + r3j + r4k +r5l + r6m + r7n + r8p
Хотя эти действия довольно сложны, мы знаем, как складывать, вычитать, умножать и делить октонионы. Каждый кватернион можно записать как особый тип октониона, у которого последние четыре коэффициента равны нулю.
Как и кватернионы, октонионы ни упорядочены, ни коммутативны. Однако октонионы ещё и не ассоциативны. Все предыдущие рассмотренные числовые системы были ассоциативными. Это значит, что для любых трёх элементов, a, b и c, два способа их перемножения, a(bc) и (ab)c, идентичны. Однако для октонионов это не так. Существуют октонионы o1, o2 и o3 такие, что o1(o2o3) ? (o1o2)o3.
Мы можем продолжить это удвоение и получить ещё большую, 16-размерную числовую систему, под названием седенионы. Для его описания потребуется 16 вещественных числ. Октонионы – это особый тип седенионов, у которых последние восемь коэффициентов равны нулю. Но исследователи чураются седенионов, поскольку у них пропадает важное свойство. Хотя их можно складывать, вычитать и умножать, не существует способа их поделить. Большинство физиков считают, что это находится за пределами «честной» математики. Даже математикам трудно управляться с ними. Можно составить и 32-мерную числовую систему, и 64-мерную, и так далее. Но о них обычно не говорят, поскольку пока что у них очень мало применений. Мы сконцентрируемся на октонионах. Подытожить все числовые системы можно при помощи этой диаграммы Венна:
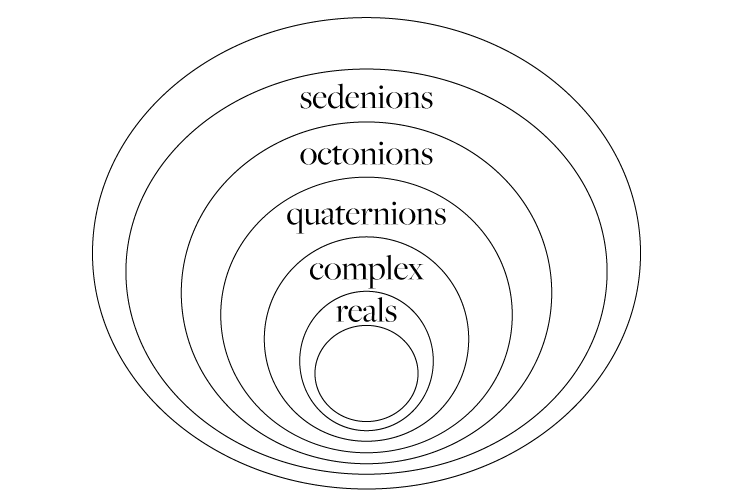
Обсудим применимость этих числовых систем. Вещественные числа используются во всех областях физики. Все величины, измерения, длины физических объектов или процессов даются в виде вещественных чисел. Хотя комплексные числа были сформулированы математиками, чтобы помочь решать уравнения (i – это решение уравнения x2 = -1), физики начали использовать комплексные числа для обсуждения волн в середине XIX века. В XX веке комплексные числа стали основой для исследований квантовой механики. Сейчас комплексные числа играют важную роль в различных областях физики. Кватернионы появляются в физике, но не играют важные роли. Октонионы, седенионы и ещё большие числовые системы редко появляются в физической литературе.
Обнаруживаемые нами законы математики
Обычный подход к рассмотрению этих числовых систем состоит в том, что вещественные числа фундаментальны, а комплексные, кватернионы и октонионы – это странные более крупные множества, которые помогают математикам и физикам чем-то заняться. Более крупные числовые системы считаются чем-то неважным и неинтересным.
Давайте перевернём этот подход с ног на голову. Вместо того, чтобы считать вещественные числа центральными, а октонионы – странной более крупной числовой системой, представим, что октонионы – фундаментальны, а другие числовые системы являются просто подмножествами октонионов. Единственная существующая числовая система – это октонионы. Перефразируя Леопольда Кронекера: «Бог создал октонионы, всё остальное – дело рук человека» [Кронекер говорил: «Бог создал целые числа, всё остальное — дело рук человека» / прим. перев.]. В октонионах содержатся все нужные нам числа. (При этом, как было показано ранее, тот же трюк мы можем проделать с седенионами и даже с 64-размерными числовыми системами. Но донесём наши идеи при помощи октонионов).
Давайте посмотрим, как можно вывести все свойства числовой системы, с которой мы знакомы. Хотя умножение октонионов не ассоциативно, если вам нужно ассоциативное умножение, можно взять особое подмножество октонионов (мы используем слово «подмножество», но нам необходим особый вид подмножества, пригодный для операций в числовой системе. Такие подмножества называются подгруппами, подполями или «поднормированными алгебрами с делением»). Так что, если выбрать подмножество всех октонионов вида
r1+ r2i + r3j + r4k + 0l + 0m + 0n + 0p
тогда умножение будет ассоциативным (как у кватернионов). Если пойти дальше и выбрать октонионы вида
r1+ r2i + 0j + 0k + 0l + 0m + 0n + 0p
тогда умножение будет коммутативным (как у комплексных чисел). Если и дальше выбрать подмножество октонионов вида
r1 + 0i + 0j + 0k + 0l + 0m + 0n + 0p
тогда из них получится упорядоченная числовая система. Все нужные аксиомы «сидят внутри» октонионов.
В этом нет ничего странного. Если у нас есть структура, мы можем сконцентрироваться на подмножестве особых элементов, удовлетворяющих определённым требованиям. Возьмём любую группу. Мы можем пройтись по всем её элементам и выбрать такие X, что для всех элементов Y будет верно XY = YX. Это подмножество – коммутативная (абелева) группа. В любой группе есть подмножество, составляющее коммутативную группу. Мы просто выбираем те части, что удовлетворяют аксиому, и игнорируем (выносим за скобки) те, что ей не удовлетворяют. Наша мысль состоит в том, что если у системы есть определённая структура, то особые подмножества системы будут удовлетворять большему количеству аксиом, чем изначальная система.
Это похоже на то, что мы делаем в физике. Мы не изучаем все явления. Мы выбираем те из них, что удовлетворяют требованиям симметрии и предсказуемости. В математике мы описываем подмножества при помощи аксиомы. В физике мы описываем выбранное подмножество явлений законом природы.
Математика для подмножества, выбранного так, чтобы удовлетворять аксиоме, проще, чем математика всего множества. Это оттого, что математики работают с аксиомами. Они доказывают теоремы и составляют модели при помощи аксиом. Когда таких аксиом нет, математика становится сложнее или вообще невозможной.
По аналогии, подмножество явлений проще объяснить законом природы, записанным языком математики. И наоборот, когда мы наблюдаем за более крупным множеством явлений, сложнее найти закон природы, и эта математика становится сложнее или вообще невозможной.
Работая в тандеме и продвигаясь вперёд
Между физикой и математикой есть важная аналогия. В обоих областях, если мы не изучаем систему в целом, но смотрим на особые подмножества, мы видим больше структуры. В физике мы берём определённое явление (обладающее симметрией), и игнорируем остальные. В математике мы рассматриваем определённые подмножества структур и игнорируем остальные. Две этих операции выноса за скобки работают сообща.
Задача физики – сформулировать функцию из набора наблюдаемых физических явлений, приводящую к математической структуре:
наблюдаемые физические явления > математическая структура
То есть, обозреваемому миру мы должны дать математическую структуру. По мере продвижения физики и того, как мы пытаемся понять всё больше наблюдаемых физических явлений, нам требуются всё большие классы математики. В понятиях этой функции, если мы хотим увеличить ввод функции, нам нужно увеличить и её вывод.
Существует множество примеров расширения физики и математики.
Когда физики начали работать с квантовой механикой, то поняли, что упорядоченные вещественные числа слишком сильно их ограничивают. Им потребовалась числовая система с меньшим количеством аксиом. Они обнаружили комплексные числа.
Когда Альберт Эйнштейн хотел описать ОТО, он понял, что математическая структура евклидова пространства с её аксиомой о плоскости (пятый постулат Евклида) была слишком ограничивающей. Ему нужно было искривлённое, неевклидово пространство, для описания пространства-времени в ОТО.
В квантовой механике известно, что в некоторых системах измерение сначала X, а затем Y, приведёт к результатам, отличным от полученных в случае, когда мы сначала измеряем Y, а затем X. Для математического описания этого необходимо выйти из уютного мира коммутативности. Им требуется более общий класс структур, не подразумевающих коммутативность.
Когда Больцман и Гиббс заговорили о статистической механике, они поняли, что получаемые ими законы уже не были детерминистскими. Результаты экспериментов уже не делились на произошло (p(X) = 1) или не произошло (p(X) = 0). Вместо этого к статистической механике требуется теория вероятностей. Шансы на определённый результат эксперимента – это вероятность, а p(X) — элемент бесконечного множества [0, 1], а не из ограниченного конечного множества {0, 1}.
Когда учёные заговорили о логике квантовых событий, они поняли, что обычная, дистрибутивная логика, слишком ограничивающая. Им необходимо было сформировать более общий класс логики, в котором аксиома дистрибутивности уже не обязательно выполнялась. Теперь это называется квантовой логикой.
Поль Дирак понял это ослабление аксиом ещё 85 лет назад, когда писал следующее:
Непрерывный прогресс физики требует для теоретических формулировок такой математики, которая постоянно продолжает усложняться. Это естественно и ожидаемо. А вот чего учёные прошлого века не ожидали, так это определённой формы, которую примет направление усложнения математики, а именно, ожидалось, что математика будет становиться всё более сложной, но будет основываться на постоянном базисе из аксиом и определений. На самом деле современное развитие физики требует математики, постоянно сдвигающей свои основы и становящейся более абстрактной. Неевклидова геометрия и некоммутативная алгебра, когда-то считавшиеся выдумкой и развлечением мыслителей, теперь оказываются необходимыми для описания общих фактов физического мира. Кажется вероятным, что этот процесс увеличения абстракции продолжится в будущем, и развитие физики будет связано с постоянным изменением и обобщением аксиом, лежащих в основе математики, а не с логическим развитием любой из математических схем, находящихся на неподвижной основе [Dirac, P.A.M. Quantised singularities in the electromagnetic field. Proceedings of the Royal Society 133, 60-72, (1931).].
С развитием физики и открытием всё большего количества явлений, требуются всё более крупные классы математических структур со всё меньшим количеством аксиом с «увеличивающейся абстракцией» и «обобщением аксиом». Без сомнения, если бы Дирак был жив, он бы писал о приходе октонионов или даже седенионов в мир необходимых числовых систем.
Для описания большего количества явлений нам нужны всё большие классы математических структур и всё меньше аксиом. Каково же логическое заключение этой тенденции? Как далеко это может зайти? Физики хотят описывать всё больше явлений в нашей Вселенной. Допустим, что мы хотим описать все явления Вселенной. Какая математика нам для этого понадобится? Сколько аксиом будет нужно математической структуре, описывающей все явления? Конечно, это сложно предсказать, но ещё сложнее не порассуждать на эту тему. Одно из возможных заключений – если мы посмотрим на всю Вселенную разом, и не будем выносить за скобки никакие подмножества явлений, то нам нужна будет математика вообще без всяких аксиом. То есть, в целом Вселенная свободна от структуры и для её описания аксиомы не нужны. Полное беззаконие! Математика без структуры – это просто множества. Это может, наконец, устранить всю метафизику, связанную с законами природы и математическими структурами. Только тот способ, которым мы изучаем Вселенную, даёт нам иллюзию наличия структуры.
С таким взглядом на физику мы приходим к ещё более сложному вопросу. Таковы будущие проекты науки. Если видимая нами структура иллюзорна и происходит из нашего способа изучения определённых явлений, почему мы её видим? Вместо того, чтобы изучать законы природы, формулируемые учёными, нам нужно изучить учёных и то, как они выбирают законы природы, подмножества явлений и всё, что с ними связано. Какое свойство человека делает его таким хорошим ситом? Вместо того, чтобы изучать Вселенную, нам нужно изучить тот способ, каким мы её изучаем.
Нозон С. Яновский – доктор математики из аспирантуры Городского университета Нью-Йорка. Профессор информатики в Бруклинском колледже Городского университета Нью-Йорка. Кроме научных работ, он был соавтором книги «Квантовые вычисления для специалистов по информатике» и написал «Внешние пределы разумного: чего наука, математика и логика не могут нам сообщить».
Комментарии (64)

StanislavHabr
25.08.2017 14:58-1Очень интересны посыл в статье. Возможно, математика на основе кватернионов даст понять нам, что такое тёмная материя и энергия.
Кстати, нельзя ни «посчитать» отношение общего количества реальных чисел к комплексным? Наподобие того, как множество всех целых чисел больше в пять раз множества целых чисел, делимых на пять без остатка.
Подозреваю, что для математика мой вопрос — вершина тупости, но всё же — а вдруг есть ответ?
CaptainFlint
25.08.2017 15:19С бесконечными множествами интуитивные понятия «больше-меньше» дают сбой. Целых чисел на самом деле ровно столько же, сколько целых чисел, делящихся на пять. Доказывается легко: каждому целому N ставим в соответствие число 5*N. В итоге все числа с обеих сторон мы разбили на пары, ни одно число не осталось забытым. Значит, чисел одинаковое количество.
А комплексных чисел (да и вообще чисел любой конечной размерности — кватернионов, октонионов и т. д.) столько же, сколько вещественных чисел.lavmax
27.08.2017 23:43Из того, что я помню, бесконечности целых чисел действительно равны. Но бесконечность вещественных чисел вроде меньше комплексных, т.к. добавляется второе измерение.

CaptainFlint
27.08.2017 23:59Новое измерение не увеличивает мощность множества.
Для простоты рассмотрим отрезок [0,1] и квадрат на комплексной плоскости [0,1]x[0,1]. Для бесконечной оси/плоскости суть не меняется, просто рассуждения будут чуть сложнее. Пусть комплексное число записано в виде десятичной дроби:
0,abc… + 0,ABC… * i
(a, b, c, A, B, C — цифры)
Строим вещественное число:
0,aAbBcC…
Получили взаимно однозначное соответствие квадрата на отрезок.
P.S. На самом деле, тут ещё надо учитывать, что десятичная запись неоднозначна, и девятка в периоде запрещена (соответствует конечной дроби с увеличенным на единицу последним перед девятками разрядом), но таких «дубликатов» лишь счётное количество, поэтому они не влияют на результат.
napa3um
25.08.2017 15:22См. «Мощность множества».

StanislavHabr
25.08.2017 15:32Обязательно гляну, спасибо. Правда, не обещаю, что что-то пойму.

vanxant
25.08.2017 15:55Если на пальцах, то есть два типа мощности бесконечных множеств.
Первое — это счётное. Если мы можем (за бесконечное время) пересчитать все элементы множества, т.е. каждому элементу выдать номер 1,2,3,..., до бесконечности, то мощность множества называется счётной.
Например, рациональные числа (обыкновенные дроби типа 3/2, -7/8 или 2139413286/2395692383) тоже имеют счётную мощность, потому что их можно перенумеровать «змейкой».
А вот иррациональные числа, и, соответственно, вещественные (множество вещественных это рациональные плюс иррациональные) — таким образом пересчитать нельзя. Не хватит номеров. Мощность вещественных чисел называется мощностью континуума. Но, на самом деле, для «посчитать» достаточно отрезка [0,1] — его можно однозначно раздвинуть на всю числовую ось, например, через тангенс.
Есть ли множества, у которых мощность больше счётной, но меньше континуума? Вот здесь взрыв мозга: мы 100% знаем, что мы не знаем. Более строго, доказано, что данный вопрос неразрешим в существующей теории множеств.
0xd34df00d
27.08.2017 21:39+1Если на пальцах, то есть два типа мощности бесконечных множеств.
Почему только два? Их на самом деле бесконечно много. Для любого бесконечного множества мощности Ni вы можете построить множество 2Ni функций из этого множества в {0; 1}. Можно показать, что они неравномощны, аналогично доказательству неравномощности счётных и вещественных (а вещественные числа являются, кстати, функциями из счётных в {0; 1}).
Кроме того, есть множества, мощность которых не равна 2N для любого N, но лично я знаю только один частный случай (сумма последовательности множеств с монотонно возрастающей мощностью), и доказать для него это мне не получилось (без аксиомы выбора, по крайней мере, а с ней скучно).erwins22
28.08.2017 08:56без аксиомы выбора между конечным и счетным множествами есть еще мощность множества.
erwins22
28.08.2017 08:50иррациональных счетное множество(это корни из чисел).
а вот трансцендентных несчетное.
вещественные это иррациональные+рациональные+трансцендентные.
CaptainFlint
28.08.2017 13:30Трансцендентные являются подмножеством иррациональных. Само название подсказывает: иррациональные — те, которые не являются рациональными. А они уже состоят из алгебраических (корни многочленов) и трансцендентных (всё остальное). Алгебраических — да, счётное количество.
erwins22
28.08.2017 13:37
CaptainFlint
28.08.2017 14:23И как это противоречит тому, что я написал? Если все трансцендентные числа являются иррациональными, это не значит, что все иррациональные являются трансцендентными.
erwins22
28.08.2017 14:35Трансцендентные являются подмножеством иррациональных.
эквивалентно утверждению Транцендентных меньше(или равно) чем иррациональных.
Ирациональное число это формула составленная из целых чисел и операций + — * / корень
CaptainFlint
28.08.2017 14:52+1эквивалентно утверждению Транцендентных меньше(или равно) чем иррациональных.
Для бесконечных множеств с понятиями «больше-меньше» надо обращаться аккуратно. Мощность множества трансцендентных чисел равна мощности множества иррациональных чисел, но при этом первое множество является собственным подмножеством второго (то есть полностью включено в него и не совпадает с ним).
Ирациональное число это формула составленная из целых чисел и операций + — * / корень
Вы же выше давали ссылку на Википедию. Почитайте, что в ней говорится про иррациональные числа. Вы путаете их с алгебраическими.

vanxant
25.08.2017 15:58+1Что касается кватернионов, то не стоит ожидать от них чего-то особенного. Эти числа хорошо изучены и активно применяются на практике. Вся современная 3D-графика построена на кватернионах. Правда, для упрощения понимания все эти непонятные мнимые единицы i,j,k просто выкинули, назвали получившееся «однородными координатами» и дали простым программистам формулы, не объясняя, как они выведены. Считайте, ребяты, не рефлексируйте)
LampTester
25.08.2017 20:16А рефлексировать, на самом деле, нет смысла. Все эти диковинные числа, начиная с комплексных, — просто способ упихать N уравнений в одно, чтобы запись влезала не за двенадцать меловых досок, а хотя бы на четыре. Все остальное — иллюзия; в итоге все равно вычисления сводятся к действиям с обычными числами. И да, действительно, это особенно хорошо заметно в программировании. :) Самый очевидный пример — если пристально рассмотреть красивый алгоритм ДПФ, который весь из себя комплексный, то в какой-то момент мы обнаружим, что по факту считаем корреляцию сигнала с семейством вполне вещественных гармонических функций…
Это напоминает мне механизм префиксов в x86, или классический цветной видеосигнал. Вроде бы и совместимость со старой системой сохраняется, и новые фичи ввести можно. :)
vanxant
25.08.2017 21:28+2Ну не всегда.
Вот те же кватернионы в 3Д-графике) Казалось бы, нафига козе баян, в смысле четвёртая координата, если у нас 3-мерное пространство, которое мы потом вообще проецируем на 2Д плоскость? Давайте её выкинем и сразу повысим скорость расчёта, например, освещения на 25% на том же железе!
А вот фиг.
Допустим, вам нужно нарисовать цветок в вазе на столе в купе поезда) При этом сам цветок задан в виде координат вершин в собственной модели цветка, а дальше нам нужно поворачивать и параллельно переносить эти координаты в систему координат камеры. Ну, сначала в координаты вазы, потом стола, потом вагона, и только потом камеры. В данном случае получается 5 поворотов и 4 переноса для каждой вершины.
В классическом трёхмерном пространстве поворот это умножение на матрицу, а перенос — сложение с вектором. Операции не коммутируют, поэтому их придётся выполнять «честно» для каждой вершины. Если у нас N вершин, то нужно 10*N операций.
В кватернионах, где исходные координаты x,y,z приписываются мнимым осям i,j,k, а по четвертой (действительной) оси берётся по умолчанию 1, и поворот, и перенос, и даже проецирование это умножение на матрицу 4х4. Умножения на матрицу между собой коммутируют, т.е. мы можем сначала перемножить все 9 и даже 10 (с проецированием) матриц между собой (и с делать это один раз), а потом умножить все вектора вершин на эту готовую единую матрицу преобразования. Т.е. нам нужно всего N+10 операций (хотя и на 1 координату больше).
Я вот не знаю, как можно вывести такие формулы, не привлекая кватернионы и матрицы, исключительно из «школьной» геометрии, особенно если мы заранее не знаем, что так вообще можно. Не, ну наверняка как-то можно, но, чтобы догадаться, нужен мегамозг. А в кватернионах это как бы естественным образом получается.LampTester
25.08.2017 22:08Ну, я бы начал с того, что упомянутое вами умножение на матрицу и сложение с вектором уже являет собой некоторую абстракцию, которая придумана для того, чтобы не забивать голову теми реальными уравнениями, которые в действительности дают интересующие нас преобразования. :)
У меня есть ощущение, что, если честно расписать уравнения всех преобразований в вашем примере исходя из элементарной геометрии, в итоге мы получим то же самое, что получаем с применением кватернионов. Правда не факт, что человек сможет сделать это. :) Скорее всего он просто запутается по дороге. Но фактически тут даже по вашему описанию происходит именно то, о чем я говорил — безумно сложные и, может быть, недоступные человеческому пониманию уравнения конструируются и решаются обходным путем.
Сходный пример, кстати, — решение дифференциальных уравнений с применением разных диковинных преобразований (Фурье, Лапласа, etc), приводящих оные к виду СЛАУ.
vanxant
25.08.2017 22:46Забавно, но я сначала тоже подумал про преобразования, правда не столько Лапласа, сколько z. Тоже, задачки, в которых в «обычной записи» кровь-кишки-интегралы, сводятся к полиномам по целым степеням z (обычно отрицательным, но хотя бы). Т.е. к более-менее «школьной» математике.
Но, правда, не смог сходу придумать «понятный всем» практический пример из теории управления. В 3д-игрушки играют примерно все, так что кватернионы как-то понятнее по фактуре.LampTester
25.08.2017 23:53Но, правда, не смог сходу придумать «понятный всем» практический пример из теории управления.
Нутк, первое, что приходит в голову при слове «Z-преобразование» — расчет рекурсивных цифровых фильтров. Правда, не уверен насчет понятности всем. Хотя программисты по идее должны бы знать, что это такое. Вообще, честно сказать, мне, как радиотехнику по диплому, Z-преобразование роднее кватернионов. :)
Я просто к тому, что нет смысла искать вселенские тайны, например, в параметре s, или z (хотя s-плоскость, в принципе, можно представить себе как совокупность синусоид с амплитудами, изменяющимися по экспоненциальному закону, и все это с разными коэффициентами). Это всего лишь инструмент, который позволяет нам эффективно решать задачи с минимальным риском сойти с ума в процессе.
Dark_Daiver
26.08.2017 14:38Вот сейчас было совсем не понятно.
>Умножения на матрицу между собой коммутируют
Я не очень хорош в математике, но умножение на матрицу не коммутативно, зато ассоциативно (https://ru.wikipedia.org/wiki/%D0%A3%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5_%D0%BC%D0%B0%D1%82%D1%80%D0%B8%D1%86)
Пусть v_i — координата вершины вазы, R_1, t_1 — поворот/перенос в систему координат стола, R_2, t_2 — поворот/перенос в систему координат вагона, R_3, t_3 — поворот/перенос в систему координат камеры
В базовом случае, новая вершина вазы в финальной системе координат будет
v'_i = R_3 * (R_2 * (R_1 * v_i + t_1) + t_2) + t_3
(три умножения на матрицу, плюс добавление смещений)
Но т.к. умножение ассоциативно
v'_i = R_3 * R_2 * R_1 * v_i + R_3 * R_2 * t_1 + R_3 * t_2 + t_3 (мог напутать чуть в формуле, но думаю идея ясна)
Или
v'_i = R' * v_i + t'
где R' = R_3 * R_2 * R_1 и t' = R_3 * R_2 * t_1 + R_3 * t_2 + t_3
Т.е. вся операция сводится к умножению на матрицу 3x3 и добавлению смещения
Вам не нужен тут кватернион.
Кстати, хороший вопрос, что быстрее при вычислении на современных CPU — «честный» поворот вершины при помощи кватерниона или умножение на матрицу поворота, с учетом векторизации
Строго говоря, вам не особо то и нужны матрицы, главное, эта сама идея о том, что повороты можно компоновать вместе, получая просто другой поворот, и идея что поворот(вектор + вектор) это одно и то же что поворот(вектор) + поворот(вектор)Dark_Daiver
26.08.2017 15:20зато ассоциативно
Забыл упомянуть — еще и дистрибутивно относительно сложения.

vanxant
27.08.2017 04:18Сама идея о том, что повороты можно компоновать вместе, получая просто другой поворот, и идея что поворот(вектор + вектор) это одно и то же что поворот(вектор) + поворот(вектор)
Повороты да. Переносы — нет. В смысле или повороты, или переносы.
Если хотите матан, то их у меня есть — читайте основы OpenGL, там всё разжевано.Dark_Daiver
27.08.2017 10:12Повороты да. Переносы — нет. В смысле или повороты, или переносы.
Почему нет? Постом выше у меня, вроде, вполне себе все получается. Если же в моих выкладках есть ошибка, то было бы здорово, если бы вы подсказали мне в чем она заключается.
читайте основы OpenGL, там всё разжевано.
У меня основная работа как раз связанна с обработкой/анализом трехмерных моделей, так что небольшой бэкграунд есть. А OpenGL я стараюсь избегать.
Aguinore
25.08.2017 15:59Во сколько раз точек на плоскости больше, чем точек на прямой, лежащей на этой плоскости?
Ведь действительные числа — это прямая в комплексной плоскости и об этом говорится в статье.overweight
25.08.2017 16:28+1Одинаково.Точнее мощность одинакова.Можно установить взаимно-однозначное соответствие
RikoNw
25.08.2017 16:00-2Эта статья расширяет сознание

zerg59
26.08.2017 09:02Маги говорят, что мы находимся внутри пузыря. Это тот пузырь, в который мы были помещены с момента своего рождения. Сначала пузырь открыт, но затем он начинает закрываться, пока не запирает нас внутри себя. Этот пузырь является нашим восприятием. Мы живем внутри него всю свою жизнь. А то, что мы видим на его круглых стенках, является нашим собственным отражением.
— Это отражение является нашей картиной мира, – сказал он. – Эта картина – описание, которое давалось нам с момента нашего рождения, пока все наше внимание не оказывалось захваченным ею, и описание не стало взглядом на мир.
150Rus
25.08.2017 16:46Для описания большего количества явлений нам нужны всё большие классы математических структур и всё меньше аксиом. Каково же логическое заключение этой тенденции? Как далеко это может зайти?
Если я правильно понимаю Теорему Гёделя о Неполноте, то логического заключения быть не может, заходить это будет бесконечно.
maslyaev
25.08.2017 20:14+1Великолепная статья, прекрасный перевод. Если какому-то приверженцу культа механистической Вселенной это всё показалось ересью, не серчайте.
Это одно из тех решений, что не включают каких бы то ни было метафизических принципов
Включают. В частности, вот это: «Нам не нужно выглядывать за пределы Вселенной в поисках причины структуры, находящейся внутри её. Нам нужно только взглянуть на то, как мы рассматриваем явления». В чистом виде то, что Мамардашвили называл философским разворотом взгляда на вещи. И дальше по тексту, когда автор применил «подход с ног на голову», оттолкнувшись от октонионов — ровно то же самое.
Мне кажется, слово «метафизика» зря используют в качестве ругательного. Да, есть на редкость тупые и безобразные метафизические системы, ну и что с того? В физике тоже есть много опровергнутых теорий, но разве это означает, что физика опровергнута в целом? Метафизика, между прочим, это треть философии (если считать по основным разделам). Рассуждать о существовании законов природы и при этом клясться, что не применяется метафизика — примерно как кодить на C и утверждать, что не применяется информатика :))
Математика без структуры – это просто множества.
«Множество» — искусственное понятие, вводимое нами для оперирования фактом однородности наблюдаемых предметов и событий (уже структура). Если идти до конца, то от него тоже следует отказаться.
beavis88
28.08.2017 18:26> «Множество» — искусственное понятие, вводимое нами для оперирования фактом однородности наблюдаемых предметов и событий (уже структура). Если идти до конца, то от него тоже следует отказаться.
Если идти дальше, это будет уже психическое растройство — ты можешь осмыслить обособленный объект, а их совокупность уже нет.
PS На самом деле в статье скорее всего под структурой понимается точное математическое понятие структуры в стиле Бурбаки (множество + довесок). У вас просто термин тот же, а смысл какой-то свой.maslyaev
28.08.2017 20:31Если идти дальше, это будет уже психическое растройство — ты можешь осмыслить обособленный объект, а их совокупность уже нет.
По-хорошему, это ещё не самое глубокое сумасшествие. «Обособленный объект» — тоже искусственное понятие ;)
На самом деле в статье скорее всего под структурой понимается точное математическое понятие структуры в стиле Бурбаки (множество + довесок). У вас просто термин тот же, а смысл какой-то свой.
Довесок — это, насколько я понял, аксиоматика, на которой будут основываться рассуждения об этом множестве. Так, или я что напутал?
Что касается аксиоматики, то множества без аксиоматики быть не может. То есть нельзя просто сказать «рассмотрим множество А». Нужно обязательно продолжить "… элементами которого являются...". Аксиоматика — прямое следствие той потребности, ради которой мы вводим множество в рассмотрение. Сами по себе множества в природе (в мире идей Платона, что ли?) не существуют, они изначально с довеском. Мы, конечно, можем раздельно поговорить о множестве А и связанной с ним аксиоматике, но нужно понимать, что множество без аксиоматики — это нонсенс. То есть имея множество, мы уже имеем структуру, и не важно, приступили мы к постижению «довеска», или ещё только собираемся.
0xd34df00d
28.08.2017 20:44+1Более того, для самого понятия множества нужна аксиоматика, ZF там какой-нибудь, а то очень быстро становится весело с брадобреями.

Aingis
25.08.2017 20:57В отличие от вещественных, комплексные числа не упорядочены. Какое из двух комплексных чисел, допустим 3 + 7.2i и 6 — 4i, больше, а какое – меньше? Очевидного ответа нет. В принципе, конечно, комплексные числа можно упорядочить, но это упорядочивание не будет соответствовать их перемножению). То, что комплексные числа не упорядочены, означает, что мы теряем структуру при переходе от вещественных к комплексным числам.
На самом деле, тут подразумевается одномерная упорядоченность. Естественно, она не натягивается на двумерное числовое множество. Это всё равно что искать «длину» фигур на плоскости. С разных сторон будут разные размеры. Точно так же можно придумать двумерную или N-мерную упорядоченность, и она будет работать.

arheops
25.08.2017 23:38Так тут и говорится, что работать будет. Но не обладает свойством устойчивости к умножению.

ilyasok
26.08.2017 01:24Люди на вселенной как муравей на человеке… Ползает и пытается думать: «какой большой муравей»! То есть пытается своими ограниченными возможностями измерить\осмыслить величину превышающую его самого в порядки.
Не бог создал человека по образу и подобию своему, а человек создал бога по образу своему и подобию… А теперь создает описание свода законов физики.
Классная статья, спасибо автору и переводчику!siens
26.08.2017 14:38-1Какой закон науки описывает создание из произвольного набора химических элементов живой клетки?

fireSparrow
26.08.2017 18:37+1siens
26.08.2017 23:54Она про возникновение органических молекул, но органический не значит живой.

fireSparrow
27.08.2017 00:12+1После возникновения самореплицирующихся нуклеиновых молекул формирование клетки из коацерватных капель и/или микросфер — процесс достаточно закономерный.
siens
27.08.2017 13:48+1Кто-нибудь это воспроизвёл в лаборатории? Кроме того, "саморепликация" и вообще "нуклеиновые молекулы" уже большой скачок по сравнению со случайными органическими молекулами спирта, сахара и аминокислот.

fireSparrow
27.08.2017 15:49+1А кто-нибудь воспроизвёл в лаборатории акт креацинизма?
Нужно понимать, что химическая эволюция происходила в масштбах целой планеты миллионы лет, а наука занимается этим вопросом всего каких-то несколько десятилетий, и её ресурсы несоизмеримы с ресурсами всей планеты.
Но даже с учётом этого, уже продемонстрированы по отдельности большинство ключевых этапов химической эволюции.
В частности
Манфред Сампер (Manfred Sumper) и Рудигер Льюс (Rudiger Luce) лаборатории Эйгена продемонстрировали, что в смеси, вообще не содержащей РНК, а содержащей только нуклеотиды и Q?-репликазу, может при определённых условиях спонтанно возникнуть самореплицирующаяся РНК

norlin
26.08.2017 18:19Эти законы кажутся нам точно подстроенными для того, чтобы смогла появиться жизнь, и, в частности, – разумная жизнь
Нет, не кажутся. Вы путаете причинно-следственную связь: такая жизнь появилась именно в результате того, что в нашей Вселенной именно такие законы.

alex_blank
27.08.2017 05:27Математика без структуры – это просто множества
Ну нет, множества это уже структуры ;)


willmore
Начиналось как графомания, в разделе про числовые системы стало интересно, к чему клонит автор. В итоге — ни к чему, закончилось опять графоманией.
и, видимо, изнасиловать их?
Что конкретно нам предлагается сделать или что мы хотим получить? Ведь нет причин менять методологию науки, т.к. она прекрасно работает по сей день.
tolkach88
Тут речь о том что законы есть только в нашем сознании, так как мы от природы даже подсознательно пытаемся найти структуру там где ее нет. Да все работает, но не обязательно по каким-то четким выверенным правилам. Скорее всего осознать реальные законы природы мы не можем в связи с тем что мы мыслим неправильно. Менять методологию не стоит — просто в процессе развития ее мы как раз и идем в сторону отсутствия структуры и понимания.
napa3um
См. «Антропный принцип».
overweight
Абсолютно согласен.Сначала удивился, как это устройство Вселенной связано со случайными формулами и рисунками на верхней картинке?)Потом какая-то непонятно к чему ведущая вода.Не понял, как это все относится к заголовку, и это главная претензия к статье.
Кстати, насчет комплексных чисел.Они упрощают решение некоторых задач, т.к. общий вид решения не меняется после прохождения параметрами некоторых пограничных значений, однако в целом можно обойтись и без них, рассматривая каждый случай отдельно.Про остальные не знаю, но предполагаю что это также.Это просто упрощает решение, но не является необходимым
SLY_G Автор
Если вы не поняли статью, это не значит, что она плохая.
overweight
Ошибаетесь, я прерасно понял мысль про то, что сокращающееся количество аксиом усложняет математику, что нам требуется все меньше и меньше аксиом для описания явлений и возможен критический случай, когда аксиом не останется вообще.Однако на этом связность текста заканчивается, замещаясь лишней историей, неуместными аналогиями между физикой и математикой.Опять же, как я уже писал, более сложные структуры вроде комплексных чисел упрощают ученым жижнь, но теоретически не являются необходимыми для описания физического мира а значит хаотичность вселенной(чтобы это бессмысленное выражение не означало), нисколько не вытекает из сомнительной возможности где-то там применить структуру, не задающуюся никакими аксиомами.
Заголовок статьи вводит в заблуждение, что речь будет идти о некоторой физической модели, исключающей мультивселеннные.Вывод не связан с заголовком.Посыл "возможно вселенная хаотична, и потому она именно такая" не имеет связи с количеством вселенных, их может быть много и все хаотичны.
andrrrrr
критический случай, когда количество аксиом станет отрицательным числом, а потом мнимым и комплексным. ну и тд.
Bronx
"+i" к неассоциативной алгебре аксиом.
bormotov
странно, что вы не дочитали буквально пару предложений
что конкретно сделать — не очень понятно, а что получить — вот же, прямым текстом: