Актуальные исследования в области предсказательного сетевого моделирования используют различные метрики, являющиеся индикаторами образования связей между агентами — однако игнорируют распределение процесса появления новых связей в сети.
В данной статье я расскажу о том, как применить точки перехода (change points) для решения Link Prediction Problem, на примере сети Flickr.

Так в статистике называют точки, в которых происходит изменение распределения некой величины. Когда речь идет о социальной сети, то один из процессов, в котором можно определить точки перехода – это процесс появления новых связей во времени в динамической сети. Для того, чтобы определить эти точки, можно использовать одну из следующих метрик: плотность графа, среднюю betweenness centrality или среднюю closeness centrality.
Давай кратко поясню суть этих трех метрик. Начнем с самого простого — плотности графа. Если в какой-то момент времени происходит резкое изменение в динамике плотности графа, то, вероятно, это связано с изменением распределения числа новых связей в зависимости от времени.
Если говорить о метриках центральности, то betweenness centrality является мерой того, как часто кратчайшие пути проходят через данную вершину, а closeness centrality выступает в качестве меры того, как быстро можно добраться из данной вершины графа во все другие.
В статье McCulloh, Matthew Webb, John Graham «Change detection in social networks» было проведено исследование международной террористической сети Аль-Каида (связей между участниками группировки) в динамике на протяжении нескольких лет. На рисунке ниже изображены характеристики сети в различные дискретные моменты времени.
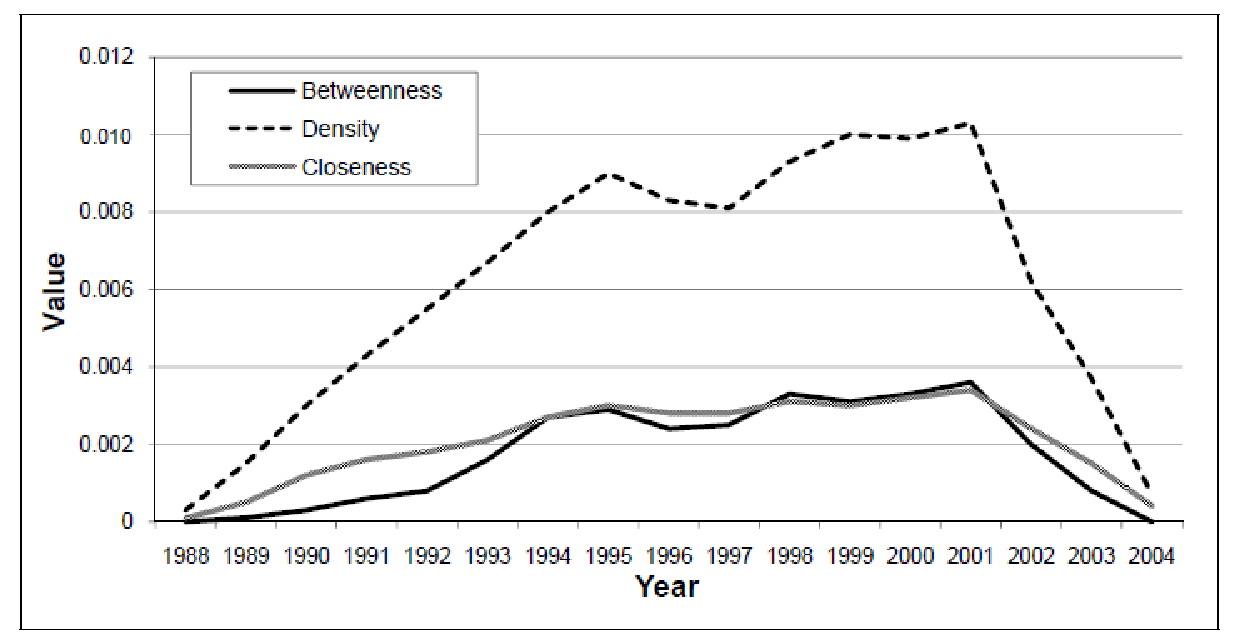
Очевидно, наблюдается предполагаемое изменение в распределении после 2001 года. Это подтверждается эмпирически, так как после терракта 11 сентября 2001 Аль-Каида была взята под жесткий контроль спецслужб мира и деятельность организации затруднилась (вместе с тем значительно замедлился рост числа связей между участниками сети). Получаем, что вышеприведенные метрики теоретически пригодны для выявления точек перехода в социальных сетях.
Попробуем предскзаать динамику связей в сети Flickr. В качестве метрик выберем коэффициент Жаккарда (метод соседства), сумму локальных коэффициентов кластеризации (метрика, основанная на свойствах вершин), значения трех основных мер центральности узла (для каждой пары вершин сумма degree centrality, сумма closeness centrality и сумма betweenness centrality) и значение кратчайшего расстояния между вершинами, взятое со знаком минус.
Предположим зависимость вероятности соединения пары вершин в следующий момент времени не только от значения метрик в предыдущий момент времени, но и в моменты с некоторым временным лагом. Данный выбор объясняется тем, что если наблюдается рост показателя того или иного классификатора со временем, то значит на каждом следующем шаге увеличивается вероятность двух вершин быть соединенными.
Отдельно отметим включение показателей, отвечающих за идентификацию точек перехода в сети. Выбор делается в пользу абсолютных значений плотности, средней betweenness centrality и средней closeness centrality, так как при использовании, к примеру, Random Forest, внутри отдельно взятого дерева по предположению пороговое значение одного из перечисленных (или нескольких) предикторов будет автоматически определять момент распределения сети.
В качестве целевой переменной выберем показатель Link – наличие или отсутствие связи между парой выбранных вершин (1 – для соединенных ребром вершин, 0 – в противном случае). Решение задачи двухклассовой классификации методом Random Forest дало следующие результаты на тестовой выборке:

В нашем случае решается не просто задача бинарной классификации на равные по значимости классы, а происходит деление на «негативный» и «позитивный» классы — поэтому мы можем использовать метрику AUC для определения качества модели. При показателе AUC = 0.88 можно сделать вывод о высоком качестве построенной модели.
Для цели содержательной интерпретации предикторов построим график динамики уменьшения индекса Джини по независимым переменным:
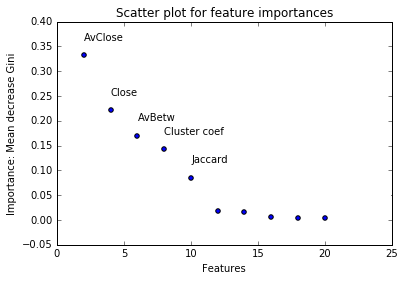
В целом, значимость показателей точек перехода говорит о том, что во время обучения в листьях дерева решения происходит разделение выборки на графы разных временных интервалов, в силу чего дальнейшее построение модели в каждой из ветвей происходит с различными пороговыми значениями для одних и тех же предикторов. Таким образом, введение метрики точки перехода способствует более точному предсказанию классов.
В данной статье я расскажу о том, как применить точки перехода (change points) для решения Link Prediction Problem, на примере сети Flickr.

Точки перехода: теория и практика
Так в статистике называют точки, в которых происходит изменение распределения некой величины. Когда речь идет о социальной сети, то один из процессов, в котором можно определить точки перехода – это процесс появления новых связей во времени в динамической сети. Для того, чтобы определить эти точки, можно использовать одну из следующих метрик: плотность графа, среднюю betweenness centrality или среднюю closeness centrality.
Давай кратко поясню суть этих трех метрик. Начнем с самого простого — плотности графа. Если в какой-то момент времени происходит резкое изменение в динамике плотности графа, то, вероятно, это связано с изменением распределения числа новых связей в зависимости от времени.
Если говорить о метриках центральности, то betweenness centrality является мерой того, как часто кратчайшие пути проходят через данную вершину, а closeness centrality выступает в качестве меры того, как быстро можно добраться из данной вершины графа во все другие.
В статье McCulloh, Matthew Webb, John Graham «Change detection in social networks» было проведено исследование международной террористической сети Аль-Каида (связей между участниками группировки) в динамике на протяжении нескольких лет. На рисунке ниже изображены характеристики сети в различные дискретные моменты времени.

Очевидно, наблюдается предполагаемое изменение в распределении после 2001 года. Это подтверждается эмпирически, так как после терракта 11 сентября 2001 Аль-Каида была взята под жесткий контроль спецслужб мира и деятельность организации затруднилась (вместе с тем значительно замедлился рост числа связей между участниками сети). Получаем, что вышеприведенные метрики теоретически пригодны для выявления точек перехода в социальных сетях.
Эксперимент с сетью Flickr
Попробуем предскзаать динамику связей в сети Flickr. В качестве метрик выберем коэффициент Жаккарда (метод соседства), сумму локальных коэффициентов кластеризации (метрика, основанная на свойствах вершин), значения трех основных мер центральности узла (для каждой пары вершин сумма degree centrality, сумма closeness centrality и сумма betweenness centrality) и значение кратчайшего расстояния между вершинами, взятое со знаком минус.
Предположим зависимость вероятности соединения пары вершин в следующий момент времени не только от значения метрик в предыдущий момент времени, но и в моменты с некоторым временным лагом. Данный выбор объясняется тем, что если наблюдается рост показателя того или иного классификатора со временем, то значит на каждом следующем шаге увеличивается вероятность двух вершин быть соединенными.
Отдельно отметим включение показателей, отвечающих за идентификацию точек перехода в сети. Выбор делается в пользу абсолютных значений плотности, средней betweenness centrality и средней closeness centrality, так как при использовании, к примеру, Random Forest, внутри отдельно взятого дерева по предположению пороговое значение одного из перечисленных (или нескольких) предикторов будет автоматически определять момент распределения сети.
В качестве целевой переменной выберем показатель Link – наличие или отсутствие связи между парой выбранных вершин (1 – для соединенных ребром вершин, 0 – в противном случае). Решение задачи двухклассовой классификации методом Random Forest дало следующие результаты на тестовой выборке:

В нашем случае решается не просто задача бинарной классификации на равные по значимости классы, а происходит деление на «негативный» и «позитивный» классы — поэтому мы можем использовать метрику AUC для определения качества модели. При показателе AUC = 0.88 можно сделать вывод о высоком качестве построенной модели.
Для цели содержательной интерпретации предикторов построим график динамики уменьшения индекса Джини по независимым переменным:

Выводы
- двумя самыми значимыми показателями оказались AvClose и Close (меры того, как быстро можно добраться из данной вершины во все другие) => эти переменные способны предсказывать именно будущие, а не настоящие связи
- в тройке лидеров по значимости находятся два показателя, которые рассчитывались не на основе индивидуальных особенностей вершин, а на основе показателей по всему графу
- значимость средних closeness и betweenness centrality говорит о том, что гипотеза наличия точек перехода подтверждается
В целом, значимость показателей точек перехода говорит о том, что во время обучения в листьях дерева решения происходит разделение выборки на графы разных временных интервалов, в силу чего дальнейшее построение модели в каждой из ветвей происходит с различными пороговыми значениями для одних и тех же предикторов. Таким образом, введение метрики точки перехода способствует более точному предсказанию классов.

