Расчёт цепей постоянного тока на пальцах, или давайте считать ЦАП для троичной логики
Но для начала неонки, какой же русский их не любит?
Итак, снова я со своими троичными железками, но в этой статье они выступают фоном, сегодня статья про резисторы. Запаял я было несколько платок, в которые можно воткнуть газоразрядные лампы типа ИН-12 или ИН-15, но часы делать не захотел :)

Простейшие платки, несут на себе пару светодиодов sk6812 для подсветки баллона, десяток транзисторов и управляющие ими 595е сдвиговые регистры. Вот так выглядит платка, несущая на себе одну лампу, но при этом их можно собирать в длинную колбасу для достижения нужного количества ламп:

Спасибо ikaktys за помощь! Одновременно с неонками развёл и запаял троичный счётчик, который я до того собирал на макетке и подробно описывал.

Напоминаю, что мой троичный счётчик использует сбалансированную троичную систему счисления, которая представляется тремя уровнями напряжения (-5, 0 и 5 вольт). Его состояние показывается двухцветными светодиодами: красный цвет — это отрицательное значение, погашенный — нулевое, а зелёный — положительное значение.
Казалось бы, этого вполне хватает, зачем тут неонки? Один мой приятель, который очень искренне интересуется, куда меня заведёт троичная дорожка, оказался дальтоником! Таким образом, мне пришлось думать над альтернативой двухцветным светодиодам. А тут и коробка неонок лежит, и десятичное отображение удобно.
Скрестить ужа и ежа, или как подружить двоичную и троичную логики
Поскольку у меня, как известно, ардуино головного мозга, то управляю неонками я при помощи ардуины. То есть, драйвер неонок работает на двоичной логике, а мне надо выводить информацию, основанную на троичной. Городить дешифраторы мне было лень, а поскольку у меня уже есть ардуина, то я решил троичный сигнал просто-напросто завести в АЦП ардуины, благо, свободных ног у неё более чем достаточно. Затем просто смотрим, в какой трети области АЦП текущая линия, и это нам даст троичное значение внутри ардуины.
Одна только незадача: ардуина хочет измерять аналоговый сигнал между землёй и пятью вольтами, а троичный сигнал имеет разброс от минус пяти до пяти. Кстати, измерить ардуиной напряжение от -5 до 5 В бывает нужно и в других областях. Например, недавно мне понадобилось измерять силу тока в обмотках двигателя постоянного тока, и датчик холла мне выдавал аккурат сигнал от -5 до 5.
То есть, мне нужно отмасштабировать уровень напряжения в два раза и сдвинуть его в положительную область. Самый простой способ это сделать — это на каждую троичную линию повесить по вот такому резисторному делителю:
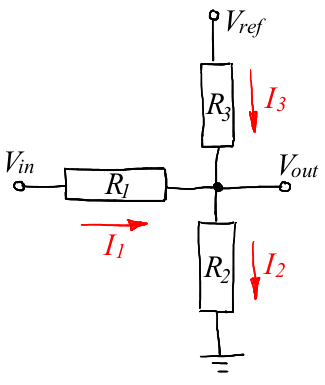
Троичный сигнал заходит в Vin (от -5 до +5 В), ардуиновское питание — это Vref (5 В), а Vout заводится на АЦП ардуины. Тут встаёт вопрос, как выбрать необходимые номиналы резисторов, чтобы Vout находился в рабочей зоне АЦП (от 0 до 5 В).
Наверное, есть люди, которые умеют это делать чуть ли не в уме, но я к ним не отношусь, да и физику знаю только на школьном уровне. Моё сокровенное знание — это то, что розетку лизать не надо. Но я умею читать, поэтому, начитавшись википедии, вооружимся законом Ома, законом Кирхгофа и умением решать линейные уравнения.
Для начала давайте поставим задачу так: зная сопротивления R1, R2 и R3, а также напряжения Vref и Vin, найти силу тока, протекающую через каждый резистор, а заодно выходное напряжение Vout.
Давайте произвольно выберем направление протекания тока (обозначено стрелочкой) через каждый резистор. Если мы «ошиблись» с выбором направления, то просто сила тока получится отрицательной.
Затем запишем закон Кирхгофа для узла цепи (тот, что жирной чёрной точкой обозначен на схеме): сумма вытекающих токов равняется сумме входящих, то есть I1+I3=I2.
Затем второе правило Кирхгофа для замкнутого контура нам говорит, что сумма напряжений на резисторах равна общей ЭДС контура.
У нас можно выбрать два контура, один с общим напряжением Vref, второй с напряжением Vin. Запишем все три уравнения:

Перепишем эту же систему в матричном виде, руками мне её решать лень, а в софте для символьных вычислений матрицы явно удобнее:

И тогда искомые токи I1, I2 и I3 можно найти, обратив матрицу 3х3 нашей системы:
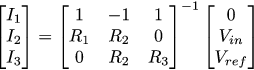
Тогда выходное напряжение Vout можно найти через только что найденный I2:

Это прекрасно, но вообще наша задача не найти Vout по известным сопротивлениям и Vin, но наоборот, зная диапазон Vin, подобрать сопротивления так, чтобы Vout укладывался между нулём и Vref.
Давайте подставим 5 вольт питания ардуины вместо Vref в наших уравнениях, выберем произвольно резистор R1 в 100кОм (у нас же делитель напряжения, поэтому один из резисторов мы можем выбрать сами). Затем запишем два уравнения: для Vin=-5 В Vout должен быть равен нулю, а для Vin=5 В Vout должен быть равен, например, 4.9 В. То есть, получили следующую систему уравнений, я специально ничего ещё в ней не упрощал:

В целом получается многочленное уравнение, можно посчитать руками, но зачем? Считать буду в sage, вот тут можно исполнить нижеприведённый код:
var("R1,R2,R3,Vin,Vout,Vref")
A=matrix([[1,-1,1],[R1,R2,0],[0,R2,R3]])
b=matrix([[0],[Vin],[Vref]])
I=(A.inverse()*b).simplify_full()
I2=I[1][0]
eq1=(4.9==(I2*R2).substitute(Vin= 5,Vref=5,R1=10^5))
eq2=(0 ==(I2*R2).substitute(Vin=-5,Vref=5,R1=10^5))
solve([eq1,eq2],R2,R3)
Вот вывод команды solve:
[[R2 == 0, R3 == 0], [R2 == 2450000, R3 == 100000]]Наши резисторы должны иметь строго положительные значения номиналов, поэтому откинем заведомо невозможные ответы. Итого, решатель нам говорит, что если мы выберем R1=R3=100 кОм, а R2=2.45 мегаома, то при питании Vref=5 В диапазон входящих напряжений Vin=[-5 В,+5 В] будет отображён в узле Vout в диапазон [0 В, 4.9 В]. Ура!
Вопрос для внимательных читателей: а почему я выбрал выходной диапазон 0-4.9 В, а не 0-5 В?
Вот код, который я использую:
#define F_CPU 16000000L
#include <avr/io.h>
#include <avr/interrupt.h>
#include <util/atomic.h>
#include <util/delay.h>
#include <stdlib.h>
#include <stdio.h>
#include <avr/pgmspace.h> // PSTR
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
#define INPUT2(port,pin) DDR ## port &= ~_BV(pin)
#define OUTPUT2(port,pin) DDR ## port |= _BV(pin)
#define CLEAR2(port,pin) PORT ## port &= ~_BV(pin)
#define SET2(port,pin) PORT ## port |= _BV(pin)
#define READ2(port,pin) ((PIN ## port & _BV(pin))?1:0)
#define INPUT(x) INPUT2(x)
#define OUTPUT(x) OUTPUT2(x)
#define CLEAR(x) CLEAR2(x)
#define SET(x) SET2(x)
#define READ(x) READ2(x)
#define WRITE(x,b) ((b)?(SET2(x)):(CLEAR2(x)))
#define SK6812_DATA_PIN B,0
#define SHIFT_595_DATA_PIN B,1
#define SHIFT_595_CLOCK_PIN B,2
#define SHIFT_595_LATCH_PIN B,3
// IN12b: 0 1 2 3 4 5 6 7 8 9 .
// IN15a: I? n % ?Y k M m + - P nc
uint16_t nixie_pins[] = {(1<<8), (1<<11), (1<<9), (1<<3), (1<<4), (1<<5), (1<<0), (1<<7), (1<<2), (1<<6), (1<<10)};
void push_nixie_symbol(uint8_t i) {
uint16_t data = nixie_pins[i];
for (int8_t j=15; j>=0; j--) {
CLEAR(SHIFT_595_CLOCK_PIN);
_delay_us(10);
if ((data>>j)&1) {
SET(SHIFT_595_DATA_PIN);
} else {
CLEAR(SHIFT_595_DATA_PIN);
}
_delay_us(10);
SET(SHIFT_595_CLOCK_PIN);
_delay_us(10);
}
}
void clock_nixie_latch() {
SET(SHIFT_595_LATCH_PIN);
_delay_us(10);
CLEAR(SHIFT_595_LATCH_PIN);
_delay_us(10);
}
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
void adc_init() {
ADMUX = (1<<REFS0); // AREF = AVcc
ADCSRA = (1<<ADEN)|(1<<ADPS2)|(1<<ADPS1)|(1<<ADPS0); // ADC Enable and prescaler of 128
}
uint16_t adc_read(uint8_t ch) {
ch &= 7; // prevent ch being >7
ADMUX = (ADMUX & 0xF8) | ch; // clear 3 lower bits before ORing
ADCSRA |= (1<<ADSC); // start single convertion
while (ADCSRA & (1<<ADSC)); // wait for the conversion to complete
return ADC;
}
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
void uart_write(char x) {
while ((UCSR0A & (1<<UDRE0))==0); // wait for empty receive buffer
UDR0 = x; // send
}
uint8_t uart_char_is_waiting() { // returns 1 if a character is waiting, 0 otherwise
return (UCSR0A & (1<<RXC0));
}
char uart_read() {
while (!uart_char_is_waiting());
char x = UDR0;
return x;
}
int uart_putchar(char c, FILE *stream __attribute__((unused))) {
uart_write(c);
return 0;
}
int uart_getchar(FILE *stream __attribute__((unused))) {
return uart_read();
}
void uart_init() {
UBRR0H = 0; // For divisors see table 19-12 in the atmega328p datasheet.
UBRR0L = 16; // U2X0, 16 -> 115.2k baud @ 16MHz.
UCSR0A = 1<<U2X0; // U2X0, 207 -> 9600 baud @ 16Mhz.
UCSR0B = 1<<TXEN0; // Enable the transmitter. Reciever is disabled.
UCSR0C = (1<<UDORD0) | (1<<UCPHA0);
fdevopen(&uart_putchar, &uart_getchar);
}
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
#define ASM_STRIP_PIN2(port,pin) "I" (_SFR_IO_ADDR(PORT ## port)), "I" (pin)
#define ASM_STRIP_PIN(x) ASM_STRIP_PIN2(x)
void __attribute__((noinline)) led_strip_write(uint8_t *colors, uint16_t count) {
cli();
while (count--) {
asm volatile(
"ld __tmp_reg__, %a0+\n"
"rcall led_strip_send_byte%=\n"
"ld __tmp_reg__, %a0+\n"
"rcall led_strip_send_byte%=\n"
"ld __tmp_reg__, %a0+\n"
"rcall led_strip_send_byte%=\n"
"rjmp led_strip_asm_end%=\n"
"led_strip_send_byte%=:\n"
"rcall led_strip_send_bit%=\n"
"rcall led_strip_send_bit%=\n"
"rcall led_strip_send_bit%=\n"
"rcall led_strip_send_bit%=\n"
"rcall led_strip_send_bit%=\n"
"rcall led_strip_send_bit%=\n"
"rcall led_strip_send_bit%=\n"
"rcall led_strip_send_bit%=\n"
"ret\n"
"led_strip_send_bit%=:\n"
"sbi %2, %3\n"
"rol __tmp_reg__\n"
"nop\n" "nop\n"
"brcs .+2\n" "cbi %2, %3\n"
"nop\n" "nop\n" "nop\n" "nop\n" "nop\n"
"brcc .+2\n" "cbi %2, %3\n"
"ret\n"
"led_strip_asm_end%=: "
: "=b" (colors)
: "0" (colors),
ASM_STRIP_PIN(SK6812_DATA_PIN)
);
}
sei();
_delay_us(80);
}
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
#define LED_COUNT 8
uint8_t red[] = {0,128,0,0,128,0,0,128,0,0,128,0,0,128,0,0,128,0,0,128,0,0,128,0};
uint8_t green[] = {128,0,0,128,0,0,128,0,0,128,0,0,128,0,0,128,0,0,128,0,0,128,0,0};
uint8_t gray[] = {128,128,128,128,128,128,128,128,128,128,128,128,128,128,128,128,128,128,128,128,128,128,128,128};
int main(void) {
OUTPUT(SHIFT_595_DATA_PIN);
OUTPUT(SHIFT_595_CLOCK_PIN);
OUTPUT(SHIFT_595_LATCH_PIN);
OUTPUT(SK6812_DATA_PIN);
CLEAR(SHIFT_595_DATA_PIN);
CLEAR(SHIFT_595_CLOCK_PIN);
CLEAR(SHIFT_595_LATCH_PIN);
CLEAR(SK6812_DATA_PIN);
adc_init();
uart_init();
FILE uart_stream = FDEV_SETUP_STREAM(uart_putchar, uart_getchar, _FDEV_SETUP_RW);
stdin = stdout = &uart_stream;
while(1) {
uint16_t v0 = adc_read(0);
uint16_t v1 = adc_read(1);
uint16_t v2 = adc_read(2);
int8_t t0 = v0<341 ? -1 : (v0>682 ? 1 : 0);
int8_t t1 = v1<341 ? -1 : (v1>682 ? 1 : 0);
int8_t t2 = v2<341 ? -1 : (v2>682 ? 1 : 0);
int8_t value = t0+t1*3+t2*9;
uint8_t ns0 = abs(value)%10;
uint8_t ns1 = abs(value)/10;
if (!ns1) ns1 = 10;
uint8_t ns2 = value>0?7:(value<0?8:10);
if (value>0) {
led_strip_write(green, LED_COUNT);
} else if (value<0) {
led_strip_write(red, LED_COUNT);
} else {
led_strip_write(gray, LED_COUNT);
}
push_nixie_symbol(ns0);
push_nixie_symbol(ns1);
push_nixie_symbol(ns2);
clock_nixie_latch();
fprintf_P(&uart_stream, PSTR("%d,%d,%d,%d, %d %d %d\r\n"), adc_read(0), adc_read(1), adc_read(2), value, ns2, ns1, ns0);
_delay_ms(100);
}
return 0;
}
А вот видео работы моего троичного счётчика с десятичным отображением текущего значения на лампах, на нём хорошо видны три одинаковых делителя, заведённые на АЦП ардуины:
Меня не очень смущает двоичность отображения, это не скомпрометирует работу моего троичного вычислителя, так как неонки не являются обязательным элементом, основной вывод предусмотрен двухцветными светодиодами.
Усложняем задачу, переходим к ЦАП
Цифро-аналоговое преобразование двоичного кода
Для начала вспомним резисторную матрицу R-2R для двоичного ЦАП, она выглядит примерно вот так:
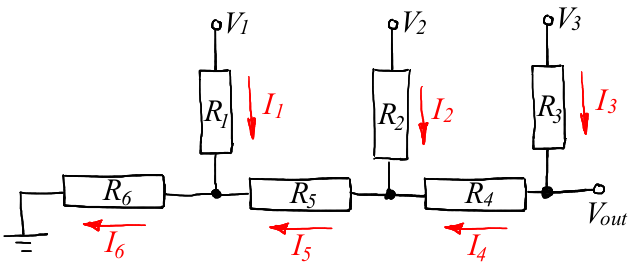
Теория нам говорит, что если мы выберем R4=R5=R, а R1=R2=R3=R6 = 2R, то, подав на входы V1, V2, V3 три бита двоичного числа, на узле Vout мы получим аналоговый уровень, соответствующий цифровому входу.
Читать энциклопедию это хорошо, но как были получены эти номиналы R и 2R? Давайте их найдём сами. Итак, топология ЦАП нам дана, как и прежде, произвольно выберем направления протекания тока через каждый резистор.
Метод расчёта у нас ровно такой же, что и в предыдущем примере: сначала посчитаем силы тока при заданных номиналах резисторов, а затем напишем несколько уравнений, которые свяжут Vout со входами V1, V2 и V3, что нам даст нужные номиналы.
Итак, узлов у нас три и контуров тоже три, в итоге шесть уравнений:

Перепишем в матричном виде:

И тогда силы токов можно найти, обратив матрицу 6х6:
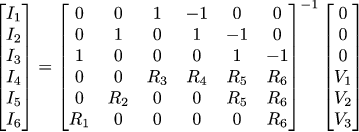
Vout может быть получена как сумма падений напряжения на трёх резисторах:
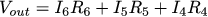
Для наглядности давайте я покажу, как выглядит Vout как функция от R1,R2,R3,R4,R5,R6 и V1,V2,V3:

Довольно неприятное выражение, правда? Ну и бог с ним, мы же не руками считать будем. Итак, при заданных номиналах резисторов у нас имеется семь ненулевых комбинаций входящих напряжений на нашем ЦАПе. Им должно соотвеетствовать семь разных значений Vout. Это даст семь уравнений, решив которые, мы получим нужные номиналы резисторов.
Как и прежде, считать будем в sage, вот код, можно запустить в браузере.
var("R1,R2,R3,R4,R5,R6,V1,V2,V3")
A=matrix([[0,0,1,-1,0,0],[0,1,0,1,-1,0],[1,0,0,0,1,-1],[0,0,R3,R4,R5,R6],[0,R2,0,0,R5,R6],[R1,0,0,0,0,R6]])
b=matrix([[0],[0],[0],[V3],[V2],[V1]])
I=(A.inverse()*b).simplify_full()
Vo=(I[5][0]*R6+I[4][0]*R5+I[3][0]*R4).simplify_full()
eq7=(7/8==Vo.substitute(V1=1,V2=1,V3=1))
eq6=(6/8==Vo.substitute(V1=0,V2=1,V3=1))
eq5=(5/8==Vo.substitute(V1=1,V2=0,V3=1))
eq4=(4/8==Vo.substitute(V1=0,V2=0,V3=1))
eq3=(3/8==Vo.substitute(V1=1,V2=1,V3=0))
eq2=(2/8==Vo.substitute(V1=0,V2=1,V3=0))
eq1=(1/8==Vo.substitute(V1=1,V2=0,V3=0))
solve([eq1,eq2,eq3,eq4,eq5,eq6,eq7],R2,R3,R4,R5,R6)
Вот вывод команды solve (я руками выбросил все решения с отрицательными и нулевыми номиналами резисторов):
[R2 == r11, R3 == r12, R4 == -1/2*r11 + r12, R5 == -1/2*R1 + r11, R6 == R1]Это означает, что мы можем резисторы R1, R2, R3 выбрать (почти) произвольно, и наш ЦАП будет работать корректно. Если мы их возьмём все три одного номинала, то и получим известную R-2R матрицу.
Цифро-аналоговое преобразование троичного кода
А теперь мы подошли к самому интересному, к разработке цифро-аналогового преобразователя для троичной сбалансированной системы. Насколько я знаю, этого ещё никто не делал, дураков мало :)
В общем, резисторная матрица прекрасно работает для двоичного кода, но что будет, если ей на вход подать троичный сигнал? Если V1=V2=V3=-1, то на выходе матрицы будет примерно -1, если V1=V2=V3=0, то на выходе ноль, а если V1=V2=V3=1, то на выходе примерно 1. То есть, в первом приближении матрица работает как нам надо. Давайте попробуем подогнать номиналы резисторов, чтобы она работала совсем хорошо.
Топология матрицы остаётся та же, выражение для Vout не изменяется, нам нужно только подкорректировать систему уравнений для поиска номиналов. Если раньше у нас было 7 уравнений, то сейчас будет 13. Давайте пробовать!
var("R,R1,R2,R3,R4,R5,R6,V1,V2,V3")
A=matrix([[0,0,1,-1,0,0],[0,1,0,1,-1,0],[1,0,0,0,1,-1],[0,0,R3,R4,R5,R6],[0,R2,0,0,R5,R6],[R1,0,0,0,0,R6]])
b=matrix([[0],[0],[0],[V3],[V2],[V1]])
I=(A.inverse()*b).simplify_full()
Vo=(I[5][0]*R6+I[4][0]*R5+I[3][0]*R4).simplify_full()
Vo=Vo.substitute(R1==R,R2==R,R3==R)
eq13=(26/27==Vo.substitute(V1= 1,V2= 1,V3= 1))
eq12=(24/27==Vo.substitute(V1= 0,V2= 1,V3= 1))
eq11=(22/27==Vo.substitute(V1=-1,V2= 1,V3= 1))
eq10=(20/27==Vo.substitute(V1= 1,V2= 0,V3= 1))
eq09=(18/27==Vo.substitute(V1= 0,V2= 0,V3= 1))
eq08=(16/27==Vo.substitute(V1=-1,V2= 0,V3= 1))
eq07=(14/27==Vo.substitute(V1= 1,V2=-1,V3= 1))
eq06=(12/27==Vo.substitute(V1= 0,V2=-1,V3= 1))
eq05=(10/27==Vo.substitute(V1=-1,V2=-1,V3= 1))
eq04=( 8/27==Vo.substitute(V1= 1,V2= 1,V3= 0))
eq03=( 6/27==Vo.substitute(V1= 0,V2= 1,V3= 0))
eq02=( 4/27==Vo.substitute(V1=-1,V2= 1,V3= 0))
eq01=( 2/27==Vo.substitute(V1= 1,V2= 0,V3= 0))
sln=solve([eq01,eq02,eq03,eq04,eq05,eq06,eq07,eq08,eq09,eq10,eq11,eq12,eq13],R4,R5,R6)
show(sln)
Как обычно, этот код можно запустить в браузере.
Ну слушайте, а ведь система имеет решение, если мы возьмём R1=R2=R3=R, R4=R5=4/3R а R6=2R, то у нас получится настоящий троичный ЦАП!
Теория теорией, но давайте проверять на практике
Для того, чтобы проверить работу ЦАПа, возьмём этот же самый троичный счётчик, что я описал чуть ранее. Тактироваться счётчик будет треугольной пилой, схема доступна тут. А три разряда нашего счётчика заведём на три входа троичного ЦАПа. Вот так выглядит тестовая схема:

На макетке сверху тактирующие треугольники, потом счётчик, на макетке снизу резисторная матрица. В этой матрице три номинала резисторов, я выбрал 1 кОм, 1.33 кОм и 2 кОм. Трёхразрядный счётчик считает от -13 до +13, на выходе я ожидаю увидеть лесенку от (примерно) -5 В до (примерно) +5 В. Тыкаюсь осциллографом:

Отлично видно, что каждый тактирующий треугольник нам генерирует очередную ступеньку лестницы. Работает!
Бонус: насколько можно доверять математическому софту?
Мы сегодня бодро считали крокодилы всякие софтом хорошим. А вообще насколько можно доверять тому, что мы насчитали? Я по работе много считаю всякого, находил баги практически во всех математических пакетах. Вот, к примеру, раз речь идёт о sage, скриншот, который я сделал два с половиной года назад, когда отправлял багрепорт:

Кто прав, численный интеграл функции f или его символьное вычисление? Они же даже разного знака! Сейчас на дворе конец 2017го года, можете проверить текущее состояние вещей. Версии сменяются, а ошибка по-прежнему на месте. Поэтому математическим софтом пользоваться, конечно, можно, но проверять результаты надо точно так же, как и после вывода формул на бумаге.
Комментарии (55)
chersanya
19.11.2017 21:12Чем вам не понравилось в первой схеме просто взять R1 = R3, а землю просто отсоединить (т.е. R2 = бесконечность)?

maxzhurkin
19.11.2017 21:22В качестве R2 тогда будет выступать сопротивление АЦП (которое, кстати, автор где-то потерял)
chersanya
19.11.2017 22:06Именно потому, что автор никак не учитывает сопротивление входа АЦП и выхода генератора, я и предложил свой вариант. Авторский тоже неточно будет работать, если неидеальностью АЦП и генератора нельзя пренебречь.

haqreu Автор
19.11.2017 22:39Ваш вариант хорош, спасибо за уточнение. Но вариант с тремя резисторами по факту является кусочком ЦАПа, о котором речь позднее :)

esaulenka
20.11.2017 00:12Не надо закладываться на входное сопротивление АЦП. Мало того, что оно толком не специфицировано, так ещё и нелинейно. АЦП «снаружи» представлено устройством выборки и хранения — по сути, маленьким конденсатором (десятки пикофарад), который непосредственно перед преобразованием заряжается от источника сигнала. И когда у нас сопротивление источника измеряется в сотнях килоом, это начинает заметно влиять на точность. В данном конкретном случае это неважно, погрешность даже в десяток процентов не важна, но в большинстве случаев этого лучше не делать.
Дополнительное чтение:
Atmel application note AVR127 www.atmel.com/Images/Atmel-8456-8-and-32-bit-AVR-Microcontrollers-AVR127-Understanding-ADC-Parameters_Application-Note.pdf (раздел 7)
ST application note AN2834 www.st.com/content/ccc/resource/technical/document/application_note/group0/3f/4c/a4/82/bd/63/4e/92/CD00211314/files/CD00211314.pdf/jcr:content/translations/en.CD00211314.pdf (сильно больше подробностей, но и читается сложнее)

haqreu Автор
19.11.2017 21:23В данном случае можно и так, но мне не всегда нужно сдвигать -5..+5 в 0..5, бывают и другие диапазоны нужны.

FGV
19.11.2017 21:16правильный ответ скорее всего тот что символьный метод насчитал, т.к. подинтегральная функция на интервале интегрирования имеет разрыв, численные методы в этом случае обычно врут

haqreu Автор
19.11.2017 21:25Если что, подынтегральная функция непрерывна.

FGV
19.11.2017 21:37вбил в эксель, при t=0 — пишет деление на 0.

haqreu Автор
19.11.2017 21:38Можете показать формулу?

FGV
19.11.2017 21:43уточнение: если считать через арктангенс — возвращает деление на 0, если через атан2 — то возвращает 0.

haqreu Автор
19.11.2017 21:44Да, я именно про это и хотел сказать. Тут важно использовать atan2.

Refridgerator
20.11.2017 06:25Функция Atan от двух переменных перед вычислением приводится к одной. В Вольфраме легко видно, если вычислить ArcTan[2, 3]:
ArcTan[3/2]

Refridgerator
20.11.2017 06:31Виноват, соврал. Это происходит только с действительными константами. Видимо, результат зависит и от того, в каких числах вычисляется численный интеграл — действительных или комплексных.

haqreu Автор
20.11.2017 08:35Даже если не использовать комплексных чисел, (кстати, у меня в примере только вещественные), то atan2 приводится к atan несколько сложнее, нежели простым делением аргументов:

Refridgerator
20.11.2017 11:19Просто я слышал, что Wolfram в своей внутренней кухне по-умолчанию считает всё в комплексных числах. По этой причине он не упрощает до x выражение Sqrt[x^2], если не задать явно, что x — действительное. Возможно, что и в Sage тоже как-то так.
mayorovp
20.11.2017 12:18Ну, atan2-то от комплексных аргументов не имеет ни определения, ни смысла…

Refridgerator
20.11.2017 12:28Я имел в виду приведение ArcTan от двух действительных аргументов к функции аргумента от одного комплексного:
ArcTan[x, y] // ComplexExpand
=
Arg[x + i y]
mayorovp
20.11.2017 09:12Численные методы врут только когда разрыв второго рода. А тут даже если atan2 на обычный арктангенс заменить — будет разрыв первого рода, который численными методами без проблем съедается.

haqreu Автор
20.11.2017 09:14Численные методы отлично врут и на непрерывных функциях. Зависит от очень многих вещей…

Alexeyslav
20.11.2017 12:15Кто прав, численный интеграл функции f или его символьное вычисление?
Я бы больше доверял символьному вычислению. Численные подвержены проблеме округления младшего разряда на каждой операции, а когда операций набираются миллионы округления приводят к существенной ошибке.
Когда-то по необходимости дял выполнения лабораторок написал себе решатель для системы линейных уравнений. Так вот на обычных числах REAL система из 20 уравнений давала погрешность численного решения в единицы!!! Применение 64-битных Extended просто немного отодвигало проблему, но не решало её в корне. Совремнные 128/256 бит FPU конечно более точны… но червячок сомнения всё же не отпускает. Особенно учесть что на численное вычисление только лишь синуса приходится довольно много операций.

mitrym
20.11.2017 12:290 — не светит

haqreu Автор
20.11.2017 12:29это вы к чему?

mitrym
21.11.2017 15:44Это я не понял, как отредактировать пост, если случайно выложил. Он наглухо уходит в модерацию. Поэтому не дописал идею, что для людей с нарушением цветовосприятия — индикатор в третьем состоянии мог бы мигать (для троичной системы). Т.е. есть, нет и мигаем.

haqreu Автор
21.11.2017 16:04Ага, ну, в принципе, почему нет. Только будет трудно отличить мигание, которое показывает состояние, от быстрой смены состояний.

IBAH_II
20.11.2017 19:18Я и «в уме» вижу, что задачка о трех резисторах не решается, и в статье происходит финт ушами!
Тут надо воспользоваться методиками о которых в Викепедии не пишут.
Составляем систему (я сразу сокращаю токи и напряжения «в уме»)
R1||R2=R3 (случай Uin =0, Uout=2.5)
R1=R3 (случай Uin =-5, Uout=0)
R2/((R1||R3)+R2)=1 (случай Uin =5, Uout=5)
Данная система не решается при положительных сопротивления, и главным образом из-за последнего уравнения. Но автор хитёр, он превращает последнее уравнение в R2/((R1||R3)+R2)=4.9/5.
Вообще то, в подобных случаях принято использовать «схему сдвига уровня на ОУ». Правда на одном ОУ получается инверсия. А лучше и правильнее, какую нибудь диодно-резисторную логику (ДРЛ) намутить.

haqreu Автор
20.11.2017 19:28Конкретно в этом случае нужно просто R2 выкинуть :)

IBAH_II
20.11.2017 19:40Согласен! Протормозил!
Но я все равно бы подумал в сторону логики, пользовать в этом случае АЦП роскошь
По моим прикидкам, реализуется на 1 транзисторе+2 резистора

FGV
20.11.2017 23:13хм, а почему только Ом и Кирхгоф? есть же более оптимизированные методы — узловых потенциалов и контурных токов

haqreu Автор
20.11.2017 23:24Просто потому, что Ома и Кирхгофа хватает. Руками мы не считаем давно, поэтому улучшения типа контурных токов не очень актуальны — для понимания сложнее, а ничего нового не дают.
mayorovp
21.11.2017 09:57Ну почему же, они дают уменьшение числа уравнений. Меньше забивать руками в решатель СЛАУ...

haqreu Автор
21.11.2017 10:10Давайте контекст не будем терять. Тому, кто знает про (и способен применить) метод контурных токов, не нужна моя шпаргалка. Поэтому в ней только Ом и Кирхгоф.

FGV
21.11.2017 17:15для понимания сложнее, а ничего нового не дают
Первая система из трех уравнений сводится к уравнению: Vout*G = J
где:
«матрица» проводимостей: G = 1/R1 + 1/R2 + 1/R3
«вектор» узловых токов: J = Vref/R3 + Vin/R1
и сходу результат: Vout = [Vref/R3 + Vin/R1] /[1/R1 + 1/R2 + 1/R3]
по моему это проще чем решать систему с тремя неизвестными.
haqreu Автор
21.11.2017 17:18Проще или сложнее — это субъективно. Как и все остальные статьи, я написал эту статью в первую очередь как шпаргалку самому себе. Мне решить систему линейных уравнений не стоит вообще ничего. А вот разобраться и, главное, потом запомнить что есть узловой ток — это небесплатно.



datacompboy
www.wolframalpha.com/input/?i=int(+sin(t)*atan2(2*sin(t),-2*cos(t)%2B1),+t%3D0..Pi)
Ответ — 3/4*Pi.
haqreu Автор
К чему этот комментарий? В вольфраме хороший решатель интегралов, не спорю. И конкретно в этом месте ошибки нет. В других местах есть.
datacompboy
К ответу на вопрос «кому верить». Численному почти всегда я доверяю больше, чем символьному.
haqreu Автор
Почему?
mayorovp
Конкретно приведенная вами функция — ограниченная и непрерывная почти всюду, но с разрывами в некоторых точках (точнее, один из ее множителей имеет разрыв в 2?k). Численным алгоритмам интегрирования на эти разрывы наплевать, а вот символьный может споткнуться и рассмотреть не ту ветку.
mayorovp
Упс, что-то про 2?k я погорячился. Но смысл тот же.
haqreu Автор
Конкретно приведённая мной функция на непрерывна на заданном промежутке интегрирования, но это не суть моего вопроса. Я удивился, почему datacompboy почти всегда больше доверяет численному интегрированию, а не только в моём примере.
mayorovp
Потому что алгоритм численного интегрирования проще и не содержит сложных ветвлений. В нем попросту труднее допустить ошибку.
haqreu Автор
Простите, но вы о каком именно алгоритме численного интегрирования? А в том алгоритме, что вы описываете, какие накладываются ограничения на подынтегральную функцию? А пользователь проверил их выполнение?
koldyr
А вы проверили их выполнение? У вас неустранимые разрывы на интервале интегрирования, например в точке pi*2/3, а значит формулу ньютона-лейбница применять нельзя.
haqreu Автор
Приведённая мной функция непрерывна на всём интервале интегрирования, в том числе в точке 2/3 ?.
koldyr
Таки да, упустил что atan2(y,x), а значит sin(t) там зажимает её. Примите мои извинения.