Проверка жизнеспособности идеи: однотритный вычислитель
Это уже четвёртая статья, по мере готовности будет продолжение. Оглавление:
- Считаем до трёх: раз (троичный мультиплексор и сумматоры)
- Считаем до трёх: два (память)
- Считаем до трёх: три (счётчики)
- Считаем до трёх: четыре (однотритный вычислитель и система команд трёхтритного)
Вот так выглядит основная железка, о которой сегодня будет идти речь (больше перемычек богу перемычек!):

Неблизкое будущее: система команд трёхтритного вычислителя
Как я и говорил, моя цель — постройка хоть и примитивной, но осязаемой программируемой железки, работающей на троичной логике. Пока что я склоняюсь к следующей системе команд, предложенной тут:
- каждая инструкция будет фиксированной длины (5 тритов)
- два трита на идентификатор инструкции, три трита (одна триада) на её параметр
NN (-4) — расширение на будущее (сложение/вычитание с переносом/заёмом, пропуск следующей команды в зависимости от флага знака и флага переноса и т.д.)
NO (-3) — передать управление на ttt (в будущем можно переключать сегменты через регистр R13)
NP (-2) — выполнить OPB ttt (универсальная бинарная команда) над R1 и R2 (две другие триады, задающие команду, берутся из R3 и R4) и установить флаг знака
ON (-1) — выполнить OPA ttt (универсальная унарная команда) над R1 (результат записать в тот же R1) и установить флаг знака
OO (0) — копирование регистров (см. далее)
OP (+1) — записать триаду в регистр R1
PN (+2) — записать триаду в регистр R2
PO (+3) — записать триаду в регистр R3
PP (+4) — записать триаду в регистр R4
Копирование регистров:
OONNN — скопировать R1 в R13
OONNO — скопировать R1 в R12
OONNP — скопировать R1 в R11
OONON — скопировать R1 в R10
OONOO — скопировать R1 в R9
OONOP — скопировать R1 в R8
OOPON — скопировать R1 в R7
OOPOO — скопировать R1 в R6
OOPOP — скопировать R1 в R5
OOONN — скопировать R1 в R4
OOONO — скопировать R1 в R3
OOONP — скопировать R1 в R2
OOOON — декремент R1 и установить флаг знака
OOOOO — проверить R1 и установить флаг знака
OOOOP — инкремент R1 и установить флаг знака
OOOPN — скопировать R2 в R1
OOOPO — скопировать R3 в R1
OOOPP — скопировать R4 в R1
OOPNN — скопировать R5 в R1
OOPNO — скопировать R6 в R1
OOPNP — скопировать R7 в R1
OOPON — скопировать R8 в R1
OOPOO — скопировать R9 в R1
OOPOP — скопировать R10 в R1
OOPPN — скопировать R11 в R1
OOPPO — скопировать R12 в R1
OOPPP — скопировать R13 в R1
Обратите внимание, что копирование производится только из/в регистр R1. Копирование между другими регистрами придётся делать в две команды, но зато три трита параметра команды копирования OO мне позволяют адресовать аж 13 регистров.
Память инструкций будет выполнена трёхпозиционными переключателями. Поскольку непосредственный параметр инструкции трёхтритный, то память команд будет адресоваться только тремя тритами, что даёт 27 инструкций, что мало. Посему будет несколько сегментов памяти инструкций, а регистр R13 будет использоваться для переключения между сегментами, что даёт шеститритную шину адреса, и реальное количество памяти команд будет ограничиваться только тем, насколько я устану эту память паять.
Один сегмент памяти команд будет набран из пятнадцати вот таких платок:

Каждая из таких платок несёт на себе 9 трёхпозиционных переключателей, для наглядности (особенно на фото) команды подсвечиваются двухцветными светодиодами.
Но прежде чем бросаться в пайку гигантских количеств (несколько сотен) тримуксов, давайте сначала попробуем сделать какой-нибудь существенно более простой вычислитель просто в качестве подтверждения того, что на этом принципе можно что-то построить.
Дело настоящего: однотритный вычислитель
Итак, упростим до максимума. Наш вычислитель будет иметь всего девять команд, каждая из которых задаётся старшим тритом I и младшим тритом J:
IJ
NN — скопировать R1 в R4
NO — скопировать R1 в R3
NP — скопировать R1 в R2
ON — декремент R1 и установить флаг знака
OO — проверить R1 и установить флаг знака
OP — инкремент R1 и установить флаг знака
PN — скопировать R2 в R1
PO — скопировать R3 в R1
PP — скопировать R4 в R1
Девятью командами получается адресовать максимум четыре регистра памяти, так что памяти будет четыре однотритных регистра и флаг знака. Памяти команд в вычислителе не будет вообще, а значит, и указатель текущей команды (счётчик) не нужен.
Собираем регистры
Железку я буду собирать и тестировать каждую её часть отдельно. Во-первых, при таком количестве и плотности проводов очень велика вероятность ошибки монтажа, а во вторых, наши восточные партнёры зачастую продают не очень качественные перемычки :)
Итак, у нас будут четыре одинаковые ячейки памяти с запоминанием по уровню, мы их подробно рассмотрели во второй статье:

Выводить наружу доступ ко всем ячейкам затруднительно и нерационально, поэтому они будут адресоваться через мультиплексор один-к-четырём. Разумеется, это просто урезанная версия мультиплексора 1-к-9. В итоге схема нашей памяти выглядит следующим образом:
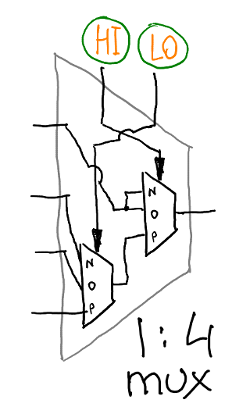
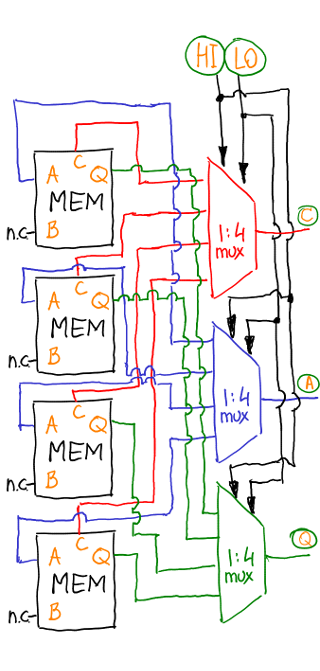
То есть, память регистров — это железка, которая на вход берёт два трита адреса, а на выход предоставляет ноги C,A,Q соответствующей ячейки памяти. Вот видео тестирования доступа к регистрам:
Адресуем правильные регистры в нужный момент
Всё копирование регистров будет происходить через промежуточный буфер. То есть, сначала содержимое регистра копируется в буфер, а затем буфер копируется в конечный регистр.Мой однотритный компьютер будет тактироваться троичной пилой, по отрицательному уровню будет происходить копирование в буфер, а по положительному обратно из буфера в память.
Вот эта схема позволяет адресовать нужный регистр памяти в нужный момент в зависимости от номера инструкции IJ и сигнала троичной пилы CLK.
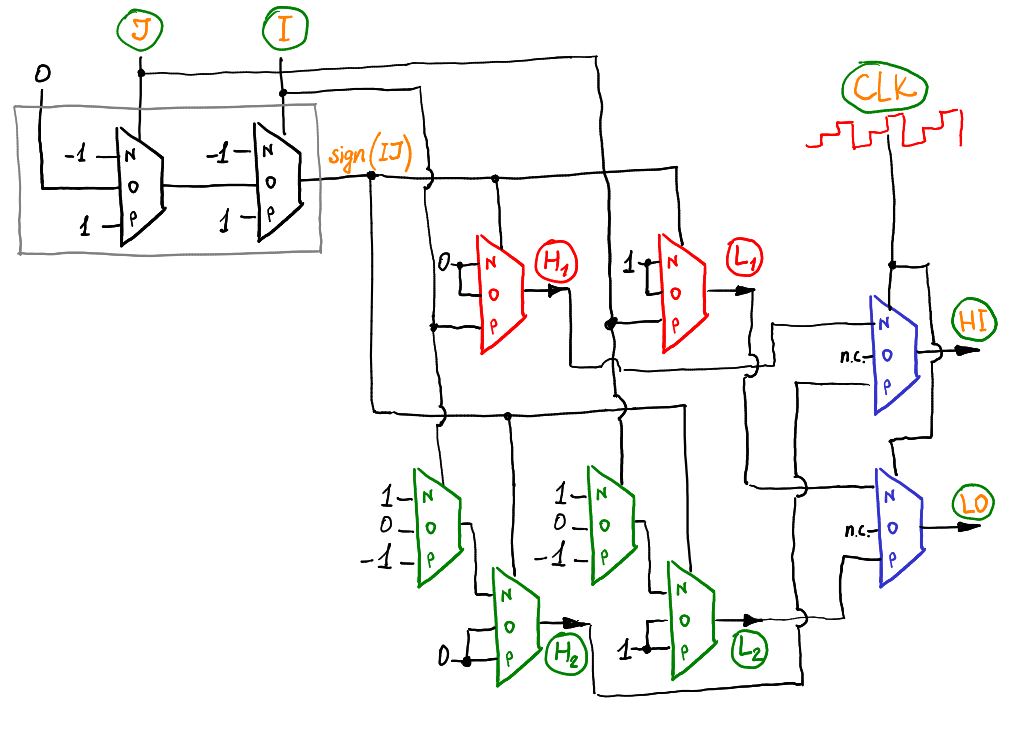
Красные мультиплексоры генерируют адрес ячейки, ИЗ которой копировать, зелёные мультиплексоры дают адрес ячейки, В которую происходит запись. Синие мультиплексоры переключают между ними в зависимости от сигнала CLK.
Вот видео тестирования работы схемы адресации памяти:
Непосредственно копирование
Поскольку генерирование нужных адресов памяти происходит само при помощи вышеописанной схемы, то для того, чтобы не загромождать схему, мы можем забыть про то, что у нас четыре регистра, и представить, что памяти только один регистр + буфер.
Копирование из регистра в буфер и обратно можно сделать крайне примитивно:
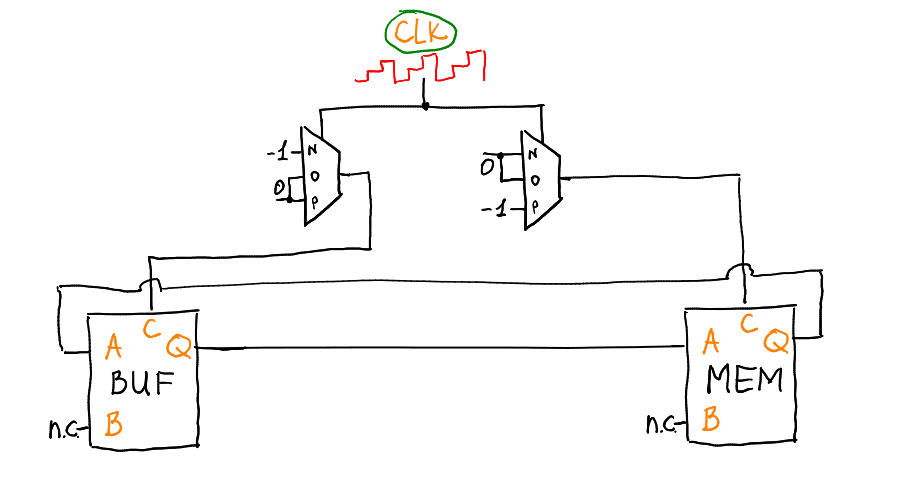
По отрицательному сигналу CLK на ногу C буфера придёт -1, а на ноге C памяти будет 0, что означает, что буфер запомнит то, что будет ему подано на ногу A. По положительному сигналу CLK всё с точностью до наоборот, скопируем содержимое буфера назад в память.
Теперь осталось вспомнить, что у нас есть не только команды копирования, но и команды увеличения/уменьшения регистра R1 на единицу. Конечная схема нашего компьютера выглядит так:
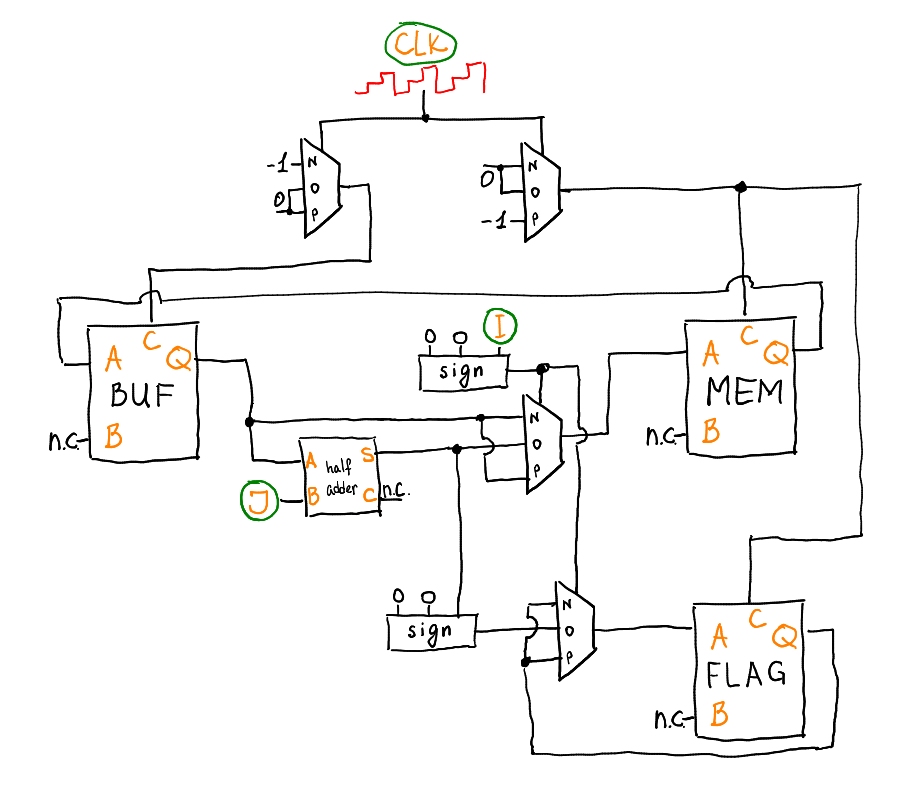
Когда старший трит команды ненулевой, то выход Q буфера подаётся напрямую на вход A памяти. Когда же он нулевой, то выход Q буфера подаётся в память через полусумматор (схему полусумматора смотрите в первой статье). Аналогично происходит и установка флага знака.
Ну а вот так выглядит железка в сборе:

А вот видео её тестирования:
Тестировать каждый кирпичик отдельно очень полезно, вот все дохлые перемычки, которые были найдены в процессе сборки только этой железки (привет нашим восточным партнёрам!)

Подведём итог
В принципе, как собирать конечный трёхтритный вычислитель вполне ясно, надо только собраться с духом и это сделать, причём, разумеется, не на макетке, так как по грубым оценкам мне на него понадобится сотни три-четыре тримуксов.
Если грубо, то АЛУ трёхтритного вычислителя будет содержать три раза последнюю схему (по одной на каждый трит). На этом, конечно, не заканчивается, так как АЛУ будет содержать по отдельной схеме на каждую команду. Итого нужно разработать остаток АЛУ, добавить ещё регистров, добавить счётчик команд, память инструкций и непосредственно схему дешифратора инструкций. Ничего неподъёмного.
Буду рад услышать новые идеи и замечания!


Boomburum
Что за программа для проектирования схем? :)
haqreu Автор
Эээ… Бумага, карандаш.
haqreu Автор
Что интересно, вы не первый, кто мне задаёт такой вопрос.
На самом деле, конечно, надо бы использовать электронное проектирование, но я не настолько усидчив, чтобы нарисовать полную схему, поэтому только вот так:
domix32
И, вот, очень жаль, что не хватает. Читать криво нарисованные схемы довольно неудобно (рисунки 1-к-4 и 1-к-9)
haqreu Автор
У меня нет рисунка 1-к-9… А в чём бы вы предложили рисовать?
andy_p
Супер. Только почему регистры нумеруются с единицы? Обычно с нуля, а для троичной арифметики, наверное, вообще как-то по другому должны нумероваться.
haqreu Автор
Ну а команды у меня нумеруются с минус четырёх :)
И именно поэтому нет нулевого регистра, т.к. знак команды даёт направление копирования.
lancrypto
Извините, я не в курсе начала обсуждения, но Вы не смотрели публикации начала 50-х? Тогда же были разработаны несколько версий троичного компьютера. Может найдете что-либо полезное.
haqreu Автор
Я не очень знаю, о чём вы конкретно, но подозреваю, что о Николае Петровиче Брусенцове и его Сетуни. У нас с ним сильно разные задачи.
Был бы благодарен, если бы вы могли точнее указать полезные публикации.
lancrypto
К сожалению, не могу, не имею точной информации. Когда-то ( с 1996 по 2006) преподавал криптографию на кафедре ЭВМ в МИИТе и там на стендах кафедры была такая информация о троичной логике в ЭВМ первых поколений. Поэтому по ассоциации с Вашей публикацией это и вспомнилось.
haqreu Автор
ЭВМ первых поколений не была полностью троичной. Большой проблемой является создание (энергонезависимой) троичной памяти, та же сетунь использовала два ферритовых колечка на трит (три состояния из четырёх).
Я же сделаю бескомпромиссно троичный вычислитель, хотя и гораздо более примитивный, нежели сетунь.
lancrypto
Удачи!
Это не троллинг.
XanderBass
Чуть яснее представилось практическое применение тернарной логики.
haqreu Автор
Не очень ясно, что именно вы имеете в виду под практическим применением. Стоящего практического применения как такового у неё нет, бинарная логика проще и надёжнее. Или вы имели в виду как именно можно что-то вычислить при помощи троичной логики?
khim
С троичными чистами такой фигни нет.
Alfacom
Увидел статью в выдаче TM Feed'a и не сразу понял, что это четвертая статья в серии, а не попытка переполнить буфер какого-нибудь калькулятора :)
cheater_ok
во время учёбы пользовались Electronics Workbench, там можно и рисовать схемы и запускать на обработку, использовали правда версию 96 года, но думаю по большей степени и сейчас она будет актуальной.
AlexanderZh
Очень познавательно и по полочкам! С нетерпением жду пятой части.