Представим, что само понятие расстояния является искусственным и не присущим реальности. Можем ли мы себе помыслить, а еще лучше визуально представить мир без расстояний? В статье предлагается один из способов это сделать при помощи нескольких математических концепций, а именно дискретного пространства, симплекса и тора. Из обсуждения этих концепций делаются несколько выводов относительно визуализации многомерных данных.

Пространство с одинаковым расстоянием между точками

Расстояние — это мера того, насколько один объект находится ближе или дальше от другого. С идеей расстояния мы сталкиваемся в самом раннем детстве, когда пытаемся дотянутся до игрушки. Потом мы начинаем ходить и ездить, развивая способность достигать объектов, находящихся все дальше и дальше от того места, где мы находимся сейчас. Целые отрасли (транспорт, почта, телекоммуникации) построены на том, что есть некие расстояния, через которые нужно перевозить людей и грузы или передавать информацию. Различные приборы, например, бинокль, позволяют сократить расстояние хотя бы визуально.

Также расстояние может быть использовано косвенно. При визуализации данных расстояние между точками и другими объектами используется, чтобы показать отношения между другими величинами. В приборах идея "ближе-дальше" выступает как аналог "холоднее-теплее" (шкала термометра), "легче-тяжелее" (шкала весов), "медленнее-быстрее" (шкала спидометра). Мы можем измерять расстояние ради него самого, как в пути, так и чтобы понять значения каких-либо переменных.

У нас нет никаких трудностей, чтобы помыслить расстояние. Более того, это получается естественным образом.

В математике расстояние связано с понятием метрического пространства. Между любыми двумя точками (элементами, объектами) метрического пространства определено расстояние (метрика). Метрика является количественным выражением отношения "ближе-дальше", то есть, отвечает на вопрос, насколько именно ближе и насколько дальше. В геометрическом и географическом смысле метрика имеет очевидный смысл и выражается в километрах, милях и тому подобных единицах. В общем смысле метрика может иметь какой-угодно смысл, например, рейтинг участников какого-нибудь конкурса. В этом случае метрикой является количество набранных баллов, а точка отсчета — первое место.

Все эти примеры нужны были для того, чтобы показать, насколько понятие расстояния важно для нашей жизни. Можем ли мы помыслить жизнь без расстояний? С приходом интернета это стало проще в части общения, но многие другие аспекты нашей жизни все еще сильно связаны с понятием расстояния. Тем не менее, мы можем создать математическую абстракцию, в которой метрика d постоянна и равна, например, единице. Такая абстракция уже существует и называется дискретным пространством X:

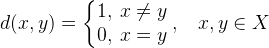
В этом определении x и y — любые две точки (элементы, объекты) пространства. Определение подразумевает, что все точки находятся одинаково далеко или одинаково близко друг от друга. Взяв любую точку мы увидим, что расстояние до любой другой одинаковое. Перемещение из точки A в точку B при прочих равных занимает одинаковое количество времени. Более того, в точке B ситуация та же самая — опять расстояние до любой другой точки будет то же самое, что и до точки A.

Дискретное пространство легко представить в виде таблицы расстояний, как это делают в автомобильном атласе. На пересечении строки и столбца в такой таблице указывается расстояние для точек, соответствующих данной строке и столбцу таблицы. Согласно определению, для дискретного пространства по диагонали такой таблицы будут идти нули, все остальные же значения единицы. Пример для пространства, состоящего из шести точек от A до F:

Или с городами (в километрах):

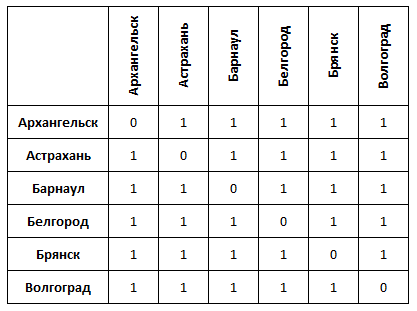
Матрицу с абстрактными точками представить себе легко, а вот с конкретными городами уже гораздо сложнее, так как мы имеем устойчивое представление о географической карте. Как же создать визуализацию, в которой нет представления о расстоянии и отношении "ближе-дальше", базового для геометрии? Попробуем изобразить дискретное пространство, начав с одной точки и добавляя точки одну за другой на одинаковом расстоянии от всех остальных.

Визуализация дискретного пространства при помощи симплекса

Для начала представим, что наше дискретное пространство состоит всего из одной точки A. Например, это может быть какое-либо состояние системы. Так как точка всего одна, то система постоянна, всегда пребывает в состоянии, соответствующем точке A. Изображение этой точки на двумерной плоскости элементарно (рядом приведена соответствующая таблица расстояний согласно определению дискретного пространства):

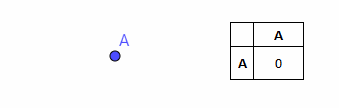
В таком пространстве никакие перемещения и изменения невозможны. Можно сказать, что такое пространство соответствует постоянному значению некоторой переменной.

Добавим еще одну точку на расстоянии, равном 1. Две точки также легко изобразить на плоскости. Вместе с расстоянием между ними они образуют отрезок AB:

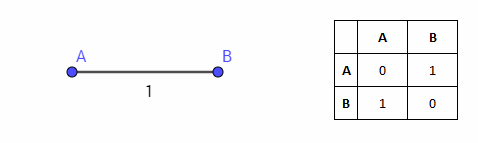
Теперь попробуем изобразить на плоскости еще одну точку, C. Ее мы должны разместить на расстоянии 1 от точек A и B, при этом сохранив расстояние 1 и между этими точками. Множество точек, равноудаленных от данной, это окружность. Если построить две окружности с единичным радиусом и центром в точках A и B, то пересечение этих окружностей даст множество точек, удаленных на единицу как от точки A, так и от точки B:

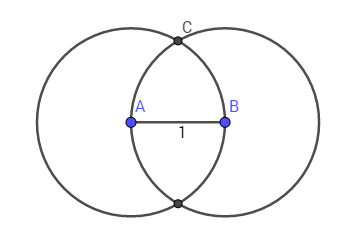
На рисунке одна из двух точек пересечений окружностей обозначена как C. Расстояние от точки C до точек A и B равно 1. Соединив все три точки, получим равносторонний треугольник ABC:

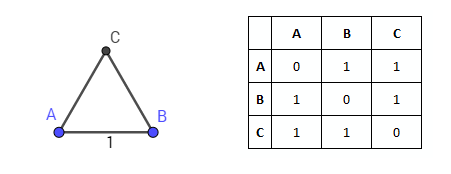
Таким образом, дискретное пространство из трех точек визуализируется на плоскости при помощи треугольника. Добавляем еще одну точку D. Можно ли построить эту точку так, чтобы три другие точки располагались от нее на одинаковом расстоянии, равном 1? Для этого должны выполнится два условия:

1. Три точки A, B и C должны лежать на окружности, проведенной из точки D
2. Радиус этой окружности должен быть равен 1

Первое условие выполняется, так как вокруг правильного треугольника можно описать окружность:

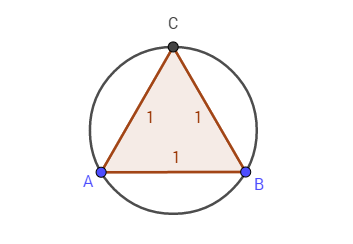
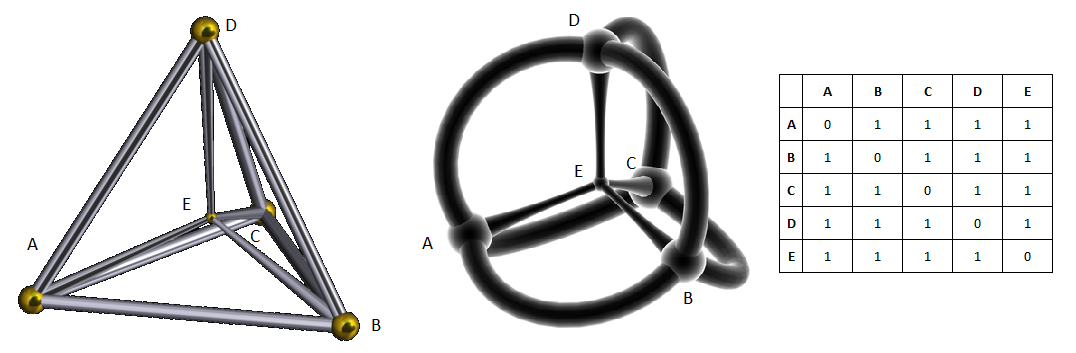
Однако, радиус описанной окружности равняется:

,

где a — длина стороны. Выходит, что четыре точки равноудаленные друг от друга изобразить на плоскости уже не получится. Чтобы выполнить второе условие, придется отодвинуть точку D от плоскости так, чтобы расстояния до точек A, B и C увеличилось до 1. В результате получим правильный тетраэдр, то есть, уже трехмерную фигуру в пространстве.

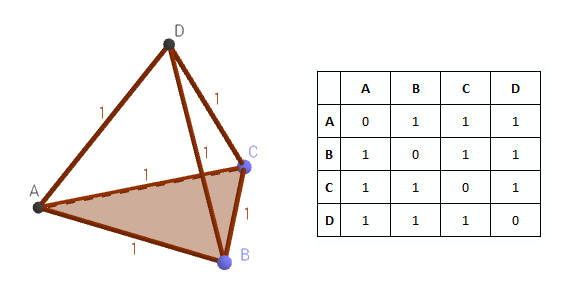
Если мы добавим еще одну точку в дискретное пространство, то снова столкнемся с проблемой, аналогичной добавлению четвертой точки к треугольнику. Теперь нам нужно будет построить единичную сферу, на которой лежат четыре точки A, B, C и D, в центр которой поместить точку E. Сферу описать вокруг правильного тетраэдра получится, но ее радиус будет отличаться от единицы:

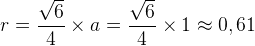
Фигура, в которой пять точек равноудалены друг от друга, называется пятиячейником (пентахором). Это уже четырехмерная фигура, трехмерная проекция которой выглядит следующим образом (слева диаграмма Шлегеля, справа стереографическая проекция, Wikipedia):

Обобщением всех построенных нами фигур, начиная с точки, является n-симплекс — простейший n-мерный многогранник с n+1 вершин:

• точка A: 0-симплекс с одной вершиной (точка — это объект с нуль-мерный объект)
• отрезок AB: 1-симплекс с двумя вершинами
• равносторонний треугольник ABC: 2-симплекс с тремя равноудаленными друг от друга вершинами
• правильный тетраэдр ABCD: 3-симплекс с четырьмя вершинами
• пятиячейник ABCDE: 4-симплекс с пятью вершинами
• и т.д.

Первые три симплекса визуализируются на плоскости как есть. Тетраэдр можно спроецировать на плоскость или сделать его 3D-модель без искажений. Пентахор можно спроецировать на плоскость с сохранением комбинаторных свойств или сделать 3D-модель с искажениями. 6-симплекс и симплексы большей размерности можно представлять в виде плоских проекций, сохраняющих комбинаторные свойства, но большей наглядности достигнуть уже не получится.

Таким образом, непосредственная визуализация дискретного пространства с большим количеством точек в двух-трех измерениях, которыми ограничена наша визуализация, затруднена. Попробуем все-таки найти какой-нибудь вариант изображения дискретного пространства с сохранением его существенных свойств хоть в каком-нибудь объеме.

Тор как 3D-визуализация дискретного пространства

До сих пор мы рассматривали визуализацию дискретного пространства как бы со стороны, представляя все точки пространства перед нами, например, на экране компьютера. При этом добились наглядности при визуализации пространства, максимум из 4-5 точек. А что если поместить наблюдателя в одну из точек пространства, например в точку A? Тогда все остальные точки, сколько бы их ни было, будут равноудалены от выбранной точки и будут располагаться на окружности единичного радиуса:

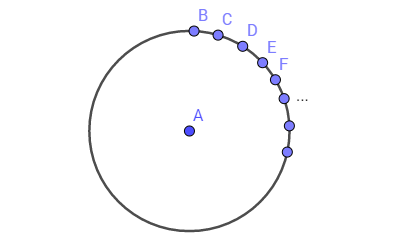
Если точек дискретного пространства бесконечно много, то их визуализация из любой выбранной точки этого пространства будет представлять собой окружность. Мы обнаружили интересную особенность дискретного пространства. Если мы находимся вне его, то чтобы его представить нужно N — 1 измерений (N — количество точек). Но как только мы оказываемся внутри дискретного пространства, то можно построить его визуализацию в двух измерениях, и эта визуализация — единичная окружность.

Аналогичная окружность строится для любой другой точки дискретного пространства. Если это сделать, по-прежнему находясь в точке A, и представляя еще одного наблюдателя в других точках, то получим следующую картину:

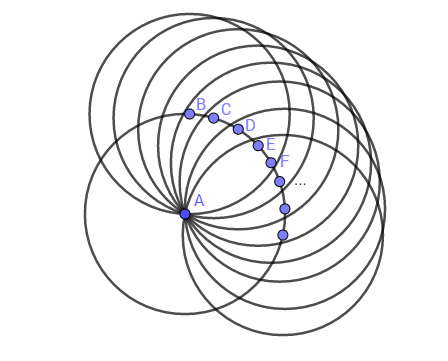
Все окружности, построенные из точек B, C и так далее, пересекаются в точке A. То есть, визуализация дискретного пространства для наблюдателей в этих точках включает в себя эту точку A.

Однако, полученная нами визуализация не очень наглядна при большом количестве точек. Задействуем третье измерение — повернем все окружности, за исключением исходной, на 90 градусов следующим образом (точка A размещена в начале координат):

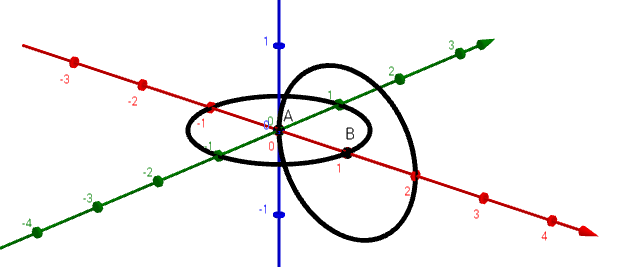
В результате мы получаем получим закрытый (самосоприкасающийся) тор в качестве 3D-визуализации дискретного пространства:

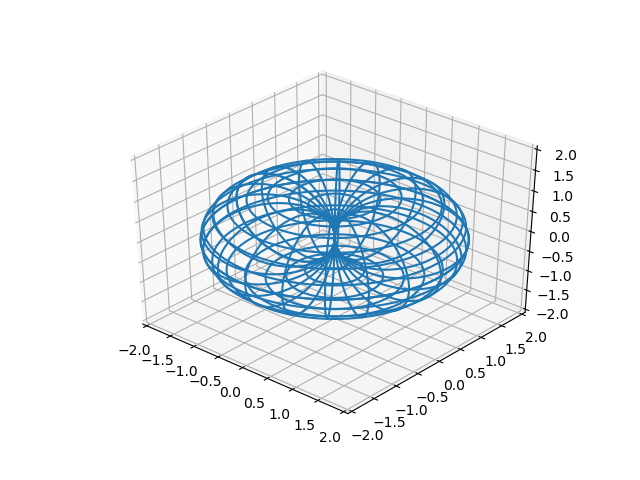
Полученная визуализация подразумевает, что наблюдатель находится в одной из точек этого пространства и представляет себе наблюдателей, находящихся в других точках пространства. Также визуализация дискретного пространства при помощи тора учитывает только отношения между точкой, в которой находится наблюдатель, и другими точками, но не между произвольными точками.

Выводы

• Размерность визуализации не всегда совпадает с размерностью визуализируемых данных или объектов (безразмерное пространство и бесконечномерная визуализация)
• Можно найти формы 3D-графики для данных и прочих объектов с размерностью большей трех, вплоть до бесконечной
• Размерность визуализации "со стороны" (снаружи визуализируемого объекта) может отличаться от размерности визуализации изнутри (из какой-либо точки объекта)