По ходу статьи, развивая идею «Одноразового блокнота», «изобретем» потоковый шифр на основе хеш-функции. Узнаем, что такое Counter Mode Encryption CTR.
Знание терминов «хеш-функция» и «Одноразовый блокнот» для чтения не обязательно.
В «Одноразовом блокноте» шифротекст получается путем наложения ключа на открытый текст. Наложение можно сделать, например, с помощью побитового XOR: каждый бит открытого текста XOR-ится с соответствующим (таким же по порядку) битом ключа.

Рис 1. Каждый бит открытого текста XOR-ится с таким же по порядку битом ключа
Соответственно для расшифровки нужно XOR-рить полученный шифротекст с ключом.
Чем более случаен и непредсказуем ключ, тем лучше, тем сложнее его подобрать. Для настоящего «Одноразового блокнота» ключ должен быть случайным:
Очевидно, что длина ключа должна быть не меньше чем длина шифруемого текста. Если ключ короче открытого текст можно попробовать его циклически повторять – рисунок 2:

Рис 2. Ключ короче открытого текста. Просто повторяем ключ что бы покрыть весь шифруемый текст
Пример метода циклического наложения гаммы
Посмотрим, что получится если текст будет длиннее ключа и мы будем просто циклически повторять гамму:
Не нужно быть криптографом что бы заметить, что шифротекст получился не слишком стойким (как минимум видно, что символы в открытом тексте повторяются):

Рис 3. Шифротекст при простом повторении гаммы нестойкий
По этой же причине блокнот называется одноразовым – нельзя использовать один и тот же ключ дважды.
Как мы убедились гамма не должна повторяться. Каждый раз, когда гамма кончается для следующего раунда нужно как-то получить новую гамму:
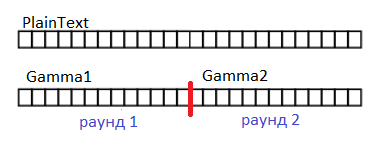
Рис 4. Каждый раз, когда гамма заканчивается нужно сделать новую гамму. В каждом раунде своя гамма
Так же мы знаем, что гамма не только не должна повторяться, но и должна быть как можно более случайной. Однако если на каждом раунде генерировать истинно случайную гамму – мы получим Одноразовый блокнот: ключ будет размером с шифротекст. Это не то, что нам надо.
Нам нужен механизм генерации псевдослучайной гаммы, зависящий от ключа. При расшифровке, зная ключ, мы должны иметь возможность сгенерировать ту же самую гамму.
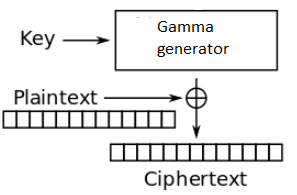
Рис 5. Схема потокового шифра
Если наш генератор будет делать псевдослучайную гамму, зависящую от ключа, для всего открытого текста – мы получим потоковый шифр.
Дополним рисунок 4: нам нужна функция, которая будет генерировать гамму в зависимости от ключа и номера раунда:
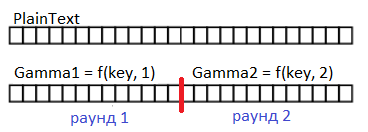
Рис 6. Гамму для каждого раунда делает функция, зависящая от ключа и номера раунда
Это и есть Counter Mode Encryption CTR – генератор гаммы на вход получает счетчик (counter) раунда:

Рис 7. 3 раунда потокового шифра при Counter Mode Encryption CTR (за исключение одного компонента, см. ниже)
Хеш функция – это функция, которая преобразует открытый текст в псевдослучайную последовательность заданной длины. Зная хеш (результат работы хеш функции) невозможно восстановить открытый текст. Изменение даже одного бита открытого текст приводит к совершенно другому, псевдослучайному хешу.
Т.е. мы можем использовать хеш функцию как генератор гаммы:
Gamma_раунда = HASH(key + RoundIndex)
Пример использования
Реализация шифра еще не закончена. В текущей реализации один и тот же ключ с одним и тем же открытым текстом всегда будет выдавать один и тот же шифротекст. Это недопустимо: представьте, что по каналу связи передаются одинаковые зашифрованные команды «срочно продавай биткоины» — это шутка, но идею вы поняли.
Итак, добавляется еще одно требование: каждый раз при шифровании должен получаться разный шифротекст. В нашем случае это означает что генератор гаммы нужно доработать.
Проблема решается путем так называемого Nonce:

Рис 8. 3 раунда потокового шифра при Counter Mode Encryption CTR с добавлением Nonce
HMAC – это способ добавить в хеш функцию зависимость от какого-нибудь дополнительного параметра. Того же результата (сделать кеш зависимым от нескольких пареметров) мы добивались с помощью конкатенации. Т.е. логически
HASH(RoundIndex + key)
То же самое что
HMAC(RoundIndex, key)
Вывод разный, а логически одно и тоже.
Кратко опишем получившейся алгоритм:
Выше описан велосипед только для образовательных целей. Идея использовать хеш-функции в потоковых шифрах не нова (см. ниже). Насколько знаю однозначного мнения о стойкости таких схем нет. Возможно, этот вопрос просто не актуален – хеши работают медленней.
В защиту идеи приведу комментарий из первичного обсуждения на pgpru.com:
использование хэша как PRF для создания потока с которым можно было бы XORить данные шифруя их не нова.
Например в описании одного из финалистов SHA3, хэш-функции Skein (http://www.skein-hash.info/sites/default/files/skein1.3.pdf) подобный use-case описан в самой PDF-ке хэша.
Если видите неточность, ошибку – отнеситесь с пониманием. Я не криптограф, ИБ занимаюсь только в прикладных целях при разработке проектов, без сверх требований к ИБ.
GitHub StreamCipherOnHashAndCTRMode
Первичное обсуждение на pgpru.com
Block cipher mode of operation
Implementing 5 modes of operation with a hash function
Теория информации и одноразовый блокнот
Потоковый шифр
Знание терминов «хеш-функция» и «Одноразовый блокнот» для чтения не обязательно.
Одноразовый блокнот
В «Одноразовом блокноте» шифротекст получается путем наложения ключа на открытый текст. Наложение можно сделать, например, с помощью побитового XOR: каждый бит открытого текста XOR-ится с соответствующим (таким же по порядку) битом ключа.

Рис 1. Каждый бит открытого текста XOR-ится с таким же по порядку битом ключа
Соответственно для расшифровки нужно XOR-рить полученный шифротекст с ключом.
var encoding = Encoding.GetEncoding(1251);
var plainText = encoding.GetBytes("111111");
var key = encoding.GetBytes("123456");
// encrypt: key XOR plainText
byte[] cipherText = new byte[plainText.Length];
new BitArray(key).Xor(new BitArray(plainText))
.CopyTo(cipherText,0);
// decrypt: key XOR chipherText
var decripted = new byte[cipherText.Length];
new BitArray(key).Xor(new BitArray(cipherText))
.CopyTo(decripted, 0);
var decriptedStr = encoding.GetString(decripted);
Листин 1. Пример работы одноразового блокнота, за исключением того, что ключ шифрования должен быть случайным
Чем более случаен и непредсказуем ключ, тем лучше, тем сложнее его подобрать. Для настоящего «Одноразового блокнота» ключ должен быть случайным:
var plainText = encoding.GetBytes("111111");
var key = new byte[6];
using (var randomGenerator = new RNGCryptoServiceProvider())
randomGenerator.GetBytes(key);
Листинг 2. Генерация случайного ключа заданной длиныКлюч должен быть одноразовым
Очевидно, что длина ключа должна быть не меньше чем длина шифруемого текста. Если ключ короче открытого текст можно попробовать его циклически повторять – рисунок 2:

Рис 2. Ключ короче открытого текста. Просто повторяем ключ что бы покрыть весь шифруемый текст
Наложения ключа на текст называют гаммированием. В этой терминологии ключ “Одноразового блокнота” будет называться гаммой.
Пример метода циклического наложения гаммы
// Потоковый XOR
// Наложить гамму на data с помощью побитового XOR,
// гамма повторяется
static IEnumerable<byte> XORStrimmed(byte[] gamma, IEnumerable<byte> data) {
var gammaIndex = 0;
foreach (var bb in data)
{
// XOR
yield return (byte)(bb ^ gamma[gammaIndex]);
if (gammaIndex < gamma.Length - 1)
gammaIndex++;
else
gammaIndex = 0;
}
}
Листинг 3. Потоковый побитовый XOR с повторением гаммыПосмотрим, что получится если текст будет длиннее ключа и мы будем просто циклически повторять гамму:
var plainText = encoding.GetBytes("11111111111111111111111111111111111111111111111111");
var key = new byte[6];
using (var randomGenerator = new RNGCryptoServiceProvider())
randomGenerator.GetBytes(key);
// encrypt: key XOR plainText
var cipherText = XORStrimmed(key, plainText);
// decrypt: key XOR chipherText
var decripted = XORStrimmed(key, cipherText);
var decriptedStr = encoding.GetString(decripted.ToArray());
Листинг 4. Получение шифротекста путем наложения повторяющейся гаммыНе нужно быть криптографом что бы заметить, что шифротекст получился не слишком стойким (как минимум видно, что символы в открытом тексте повторяются):

Рис 3. Шифротекст при простом повторении гаммы нестойкий
По этой же причине блокнот называется одноразовым – нельзя использовать один и тот же ключ дважды.
Такой открытый текст в примере выбран для наглядности. Хороший шифр, даже для такой строки, выдаст шифротекст без повторяющихся паттернов.
Потоковый шифр
Как мы убедились гамма не должна повторяться. Каждый раз, когда гамма кончается для следующего раунда нужно как-то получить новую гамму:

Рис 4. Каждый раз, когда гамма заканчивается нужно сделать новую гамму. В каждом раунде своя гамма
Так же мы знаем, что гамма не только не должна повторяться, но и должна быть как можно более случайной. Однако если на каждом раунде генерировать истинно случайную гамму – мы получим Одноразовый блокнот: ключ будет размером с шифротекст. Это не то, что нам надо.
Нам нужен механизм генерации псевдослучайной гаммы, зависящий от ключа. При расшифровке, зная ключ, мы должны иметь возможность сгенерировать ту же самую гамму.

Рис 5. Схема потокового шифра
Если наш генератор будет делать псевдослучайную гамму, зависящую от ключа, для всего открытого текста – мы получим потоковый шифр.
Counter Mode Encryption CTR
Дополним рисунок 4: нам нужна функция, которая будет генерировать гамму в зависимости от ключа и номера раунда:

Рис 6. Гамму для каждого раунда делает функция, зависящая от ключа и номера раунда
Это и есть Counter Mode Encryption CTR – генератор гаммы на вход получает счетчик (counter) раунда:

Рис 7. 3 раунда потокового шифра при Counter Mode Encryption CTR (за исключение одного компонента, см. ниже)
Хеш функция как гамма генератор
Хеш функция – это функция, которая преобразует открытый текст в псевдослучайную последовательность заданной длины. Зная хеш (результат работы хеш функции) невозможно восстановить открытый текст. Изменение даже одного бита открытого текст приводит к совершенно другому, псевдослучайному хешу.
Т.е. мы можем использовать хеш функцию как генератор гаммы:
Gamma_раунда = HASH(key + RoundIndex)
private static IEnumerable<byte> XorCounterModeEncryptDecrypt(byte[] keyBytes, IEnumerable<byte> data)
{
if (keyBytes == null) throw new ArgumentNullException(nameof(keyBytes));
if (data == null) throw new ArgumentNullException(nameof(data));
int roundIndex = 0;
byte[] roundGamma = null;
int gammaIndex = 0;
foreach (var d in data)
{
if (gammaIndex == 0)
{
// create gamma
var counterBlock = keyBytes.Concat(BitConverter.GetBytes(roundIndex)).ToArray();
using (var sha = new SHA512Managed())
roundGamma = sha.ComputeHash(counterBlock);
}
yield return (byte)(d ^ roundGamma[gammaIndex]);
if (gammaIndex < roundGamma.Length - 1)
gammaIndex++;
else
{
gammaIndex = 0;
roundIndex++;
}
} // foreach
}
Листинг 5. Потоковый побитовый XOR, с генерацией гаммы для каждого раунда с помощью хеш функцииПример использования
var plainText = encoding.GetBytes("11111111111111111111111111111111111111111111111111");
var key = encoding.GetBytes("1123456");
// encrypt: key XOR plainText
var cipherText = XorCounterModeEncryptDecrypt(key, plainText);
// decrypt: key XOR chipherText
var decripted = XorCounterModeEncryptDecript(key, cipherText);
var decriptedStr = encoding.GetString(decripted.ToArray());
Листинг 6. Шифрование/дешифрование с использованием Counter Mode Encryption потокового шифраNonce, HMAC
Реализация шифра еще не закончена. В текущей реализации один и тот же ключ с одним и тем же открытым текстом всегда будет выдавать один и тот же шифротекст. Это недопустимо: представьте, что по каналу связи передаются одинаковые зашифрованные команды «срочно продавай биткоины» — это шутка, но идею вы поняли.
Итак, добавляется еще одно требование: каждый раз при шифровании должен получаться разный шифротекст. В нашем случае это означает что генератор гаммы нужно доработать.
Проблема решается путем так называемого Nonce:
- каждый раз, при шифровании, генерируется случайная последовательность бит – Nonce
- Nonce участвует при формировании гаммы
- Gamma_раунда = HASH(Nonce + key + RoundIndex)
- Nonce один и тоже для всех раундов
- Nonce распространяется/хранится вместе с шифротекстом. Т.е. знание Nonce, который был использован при создании шифротекста, не является секретом.

Рис 8. 3 раунда потокового шифра при Counter Mode Encryption CTR с добавлением Nonce
HMAC – это способ добавить в хеш функцию зависимость от какого-нибудь дополнительного параметра. Того же результата (сделать кеш зависимым от нескольких пареметров) мы добивались с помощью конкатенации. Т.е. логически
HASH(RoundIndex + key)
То же самое что
HMAC(RoundIndex, key)
Вывод разный, а логически одно и тоже.
private static IEnumerable<byte> XorCounterModeEncryptDecrypt(byte[] keyBytes, byte[] nonceBytes, IEnumerable<byte> data)
{
if (keyBytes == null) throw new ArgumentNullException(nameof(keyBytes));
if (data == null) throw new ArgumentNullException(nameof(data));
if (nonceBytes == null) throw new ArgumentNullException(nameof(nonceBytes));
if (nonceBytes.Length < 4) throw new ArgumentOutOfRangeException(nameof(nonceBytes));
var nonce = new BitArray(nonceBytes);
int roundIndex = 0;
byte[] roundGamma = null;
int gammaIndex = 0;
foreach (var d in data)
{
if (gammaIndex == 0)
{
// create gamma
// create counter block: Nonce + Counter
// another way: Nonce XOR Counter (has some constraints)
var counterBlock = nonceBytes.Concat(BitConverter.GetBytes(roundIndex)).ToArray();
using (var hmacSHA = new HMACSHA512(keyBytes))
roundGamma = hmacSHA.ComputeHash(counterBlock);
}
yield return (byte)(d ^ roundGamma[gammaIndex]);
if (gammaIndex < roundGamma.Length - 1)
gammaIndex++;
else
{
gammaIndex = 0;
roundIndex++;
}
} // foreach
}
Листинг 7. Потоковый побитовый XOR, с генерацией гаммы для каждого раунда с помощью хеш функции. Используется Nonce и HMACvar plainText = encoding.GetBytes("11111111111111111111111111111111111111111111111111");
var key = encoding.GetBytes("1123456");
var nonce = new byte[4];
using (var randomGenerator = new RNGCryptoServiceProvider())
randomGenerator.GetBytes(nonce);
// encrypt: key XOR plainText
var cipherText =
nonce.Concat(
XorCounterModeEncryptDecrypt(key, nonce, plainText)
);
// decript: key XOR chipherText
var decripted = XorCounterModeEncryptDecrypt(
keyBytes: key,
nonceBytes: cipherText.Take(4).ToArray(),
data: cipherText.Skip(4));
var decriptedStr = encoding.GetString(decripted.ToArray());
Листинг 8. Пример использованияАлгоритм
Кратко опишем получившейся алгоритм:
- Делаем случайный Nonce. Один Nonce используется для всех раундов
- Для каждого раунда вычисляем уникальный CounterBlock, который будет использован для генерации гаммы.
CounterBlock = Nonce + НомерРаунда - Генерируем гамму для раунда
Gamma = HMAC(CounterBlock, Key) - Накладываем Gamm-у на открытый текст с помощью побитового XOR
- Когда гамма заканчивается, начинается следующий раунд. Увеличиваем НомерРаунда на 1 –таким образом новый раунд получает новую гамму
Disclaimer
Выше описан велосипед только для образовательных целей. Идея использовать хеш-функции в потоковых шифрах не нова (см. ниже). Насколько знаю однозначного мнения о стойкости таких схем нет. Возможно, этот вопрос просто не актуален – хеши работают медленней.
В защиту идеи приведу комментарий из первичного обсуждения на pgpru.com:
использование хэша как PRF для создания потока с которым можно было бы XORить данные шифруя их не нова.
Например в описании одного из финалистов SHA3, хэш-функции Skein (http://www.skein-hash.info/sites/default/files/skein1.3.pdf) подобный use-case описан в самой PDF-ке хэша.
Если видите неточность, ошибку – отнеситесь с пониманием. Я не криптограф, ИБ занимаюсь только в прикладных целях при разработке проектов, без сверх требований к ИБ.
Ссылки
GitHub StreamCipherOnHashAndCTRMode
Первичное обсуждение на pgpru.com
Block cipher mode of operation
Implementing 5 modes of operation with a hash function
Теория информации и одноразовый блокнот
Потоковый шифр
Комментарии (3)

Deosis
23.01.2018 07:12Использование гаммирования удобно тем, что функция шифрования обратна сама себе,
то есть повторное шифрование с теми же параметрами = дешифрование.
В других методах для дешифрования нужна либо отдельная функция, либо инвертированный ключ.


Gekus
Привет. По английски — encrYption. Поправьте, пожалуйста