Основой этой книги стал курс Принстонского университета, который читали гуманитариям три знаменитых астрофизика — Нил Деграсс Тайсон, Майкл Стросс и Джон Ричард Готт. Они рассказывают о том, что любят больше всего, и рассказывают так, что самые сложные теории становятся понятны неспециалистам.

Астрономы не привыкли усложнять то, что может быть простым. Большие красные звезды — это красные гиганты. Маленькие белые звезды — это белые карлики. Если звезда пульсирует, она называется пульсар. Даже начало всего пространства, времени, материи и энергии, что существуют в космосе, можно назвать всего двумя простыми словами: Большой Взрыв.

Что мы знаем о Вселенной? Наша Вселенная велика. Наш Космос гораздо больше, чем кажется. Он жарче, чем вы думаете. Плотнее, чем вы думаете. Разреженнее, чем вы думаете. Что бы вы ни думали о Вселенной, реальность все равно окажется невероятнее.

Здесь мы представим отрывок из книги «Космические струны, кротовые норы и путешествия во времени».

С тех пор как я исследую проблему путешествий во времени в рамках общей теории относительности, соседские дети думают, что у меня в гараже стоит машина времени. Однажды я побывал в Калифорнии на конференции по космологии и явился туда в бирюзовой спортивной куртке. Мой коллега Роберт Киршнер, в ту пору возглавлявший астрономический факультет в Гарварде, подошел и сказал: «Рич, ты, должно быть, купил эту куртку в будущем и привез сюда, ведь такого цвета еще не изобрели!» С тех пор я называю ее «куртка из будущего» и всегда прихожу в ней читать лекции о путешествиях во времени.

Обычно я вхожу на такую лекцию в этой бирюзовой куртке и несу коричневый брифкейс. Кладу брифкейс в шкафчик и поспешно выхожу. Затем возвращаюсь в футболке. Объясняю собравшимся, что у меня назначена другая встреча, и я договорился, чтобы эту лекцию прочитал вместо меня приглашенный оратор, затем выхожу снова. Снова возвращаюсь, уже в бирюзовой куртке, и говорю всем, что это «куртка из будущего». Объясняю, что не мог прочесть лекцию, потому что спешил на другую встречу, которая была назначена на то же время, что и лекция; но поскольку у меня есть машина времени, после встречи я смог просто отправиться в будущее, купить там куртку и вернуться сюда — прочесть лекцию, но уже успев немного постареть.

Тут я замечаю, что забыл принести конспект лекции о путешествиях во времени. Что же делать? Поскольку у меня есть машина времени, соображаю я, можно взять конспект уже на следующий день (после лекции) и вернуться сюда, заранее оставить где-нибудь в аудитории брифкейс с конспектом. Осматриваюсь, но нигде их не вижу. Итак, возможно, я их спрятал. Где? Да хоть в этом шкафчике. Открываю шкафчик, нахожу в нем брифкейс, открываю его — ура! Там лежит конспект лекции о путешествиях во времени.

Рассмотрим эти события, проследив их мировые линии на пространственно-временном графике. По оси абсцисс откладывается пространство, по оси ординат — время, причем будущее находится вверху. Аудитория, в которой я читаю лекцию, — это вертикальная полоса в центре. Вот как выглядит моя мировая линия (рис. 21.1).


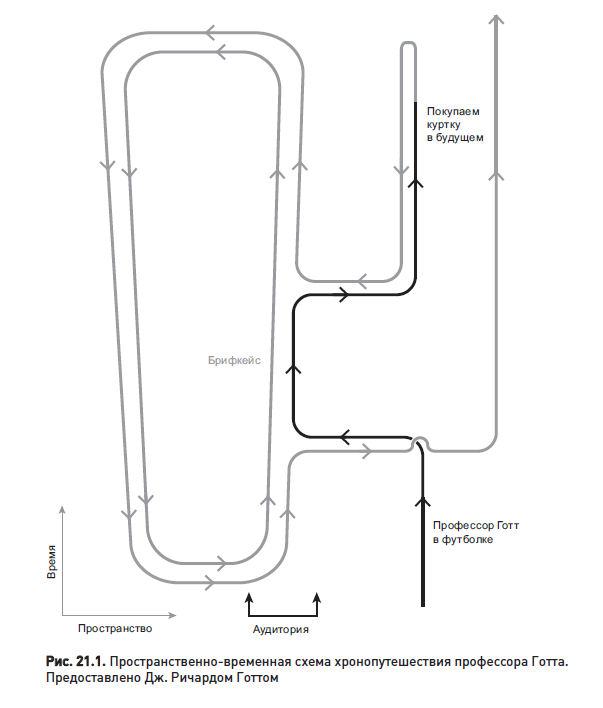
На пространственно-временном графике я выхожу из аудитории, при этом на мне белая футболка. Ненадолго возвращаюсь в аудиторию, говорю, что не смогу прочитать лекцию, потому что спешу на встречу. Удаляюсь, успеваю на встречу, а затем лечу в будущее, где покупаю куртку. С этого момента моя мировая линия становится светло-серой. Возвращаюсь, вновь захожу в аудиторию и там читаю лекцию. Когда лекция закончена, мне нужно вернуться в прошлое незадолго до начала лекции, просто чтобы успеть занести брифкейс с конспектом этой лекции. Я войду в аудиторию, а затем быстро выйду, после чего в нее войду я же (чуть младше), в футболке. Далее я продолжу жить строго в направлении будущего. У меня получилась сложная мировая линия.

А что насчет мировой линии брифкейса? Он оказывается у меня в руках, как только я нахожу его в шкафчике. Если я буду просто держать его, то он отправится в хронопутешествие вместе со мной, и я принесу его в аудиторию еще до того, как найду в шкафчике. Мировая линия брифкейса получится кольцевой. Мировая линия брифкейса странная — у нее ни начала, ни конца. У моей мировой линии есть начало (я родился) и конец (я умер), но мировая линия брифкейса — замкнутая петля. Брифкейс в данном случае можно сравнить с частицей-джинном. Действительно, она, как и джинн, возникает из ниоткуда.

Брифкейс все время у меня на виду. Он не попадает на фабрику брифкейсов. Физики, исследующие путешествия в прошлое, вынуждены учитывать частицы-джинны, когда рассуждают о квантовых эффектах. Что, если на моем брифкейсе появится небольшая потертость, когда я заберу его с собой с лекции? Игорь Новиков считает, что такой износ, который претерпевает джинн-частица, должен в какой-то момент «исправляться», чтобы она вернулась в исходное состояние, — и мой брифкейс не исключение. При этом не нарушаются законы энтропии, так как брифкейс — это не изолированная система; энергия, необходимая на его починку, поступает извне.

Информация также может выступать в качестве джинна. Допустим, я прилетаю в 1915 год и даю Эйнштейну верные уравнения поля для общей теории относительности. Он может их записать и опубликовать. Откуда взялась эта информация? Я усвоил ее из статьи Эйнштейна, а Эйнштейн узнал ее от меня. Получается кольцевая мировая линия.

Законы физики допускают существование джинн-частиц — просто их возникновение маловероятно, — причем чем массивнее и сложнее такие частицы, тем менее вероятно их возникновение. Аналогичная история могла бы произойти, если бы я нашел на полу в поточной аудитории клочок бумаги и взял с собой не брифкейс, а этот клочок. В таком случае бумажка стала бы джинном, а носить ее с собой проще, чем брифкейс. Еще проще — я мог бы банально взять электрон и унести его с собой, а затем вернуть в прошлое, в лекционную аудиторию. Просто не столь вероятно найти для этой цели такой массивный объект, как брифкейс, да еще с конспектами к лекции о путешествиях во времени. Думаю, возможны и такие сложные джинны, но возникать они будут исключительно редко.

Путешествие в прошлое происходит при наличии мировой линии, которая закольцовывается в прошлое. Обычная ситуация отражена на рис. 18.1: мировые линии Земли и других планет идут по спирали вдоль мировой линии Солнца. Ничто не может двигаться со сверхсветовой скоростью, и все мировые линии устремлены в будущее. На рис. 21.2 показана ситуация, когда мы путешествуем в прошлое. Мировая линия путешественника замыкается сама на себя, и он становится свидетелем каких-то событий из собственного прошлого. Путешественник начинает путь внизу (в прошлом) и поднимается вверх до тех пор, пока не встречает повзрослевшего себя, который ему говорит: «Привет! Я — это ты в будущем! Прилетел в прошлое поздороваться с тобой». Он отвечает: «Правда?» и отправляется по петле обратно в прошлое. Затем он встречает себя же в юности и говорит: «Привет! Я — это ты в будущем! Прилетел в прошлое поздороваться с тобой». Молодой «двойник» отвечает: «Правда?» Путешественник во времени участвует в этой встрече дважды: как молодой и как более взрослый человек, но сама ситуация складывается лишь однократно. Можно сравнить ее с четырехмерной скульптурой, на которую нанесены мировые линии. Она никогда не меняется: именно так и выглядит вся картина. Если вам интересно, как ощущалась бы подобная ситуация, — просто проведите пальцем по мировой линии и посмотрите, какие еще мировые линии с ней пересекутся.

Здесь открывается один из варантов решения знаменитого парадокса бабушки: что бы случилось, если бы я отправился в прошлое и случайно убил собственную бабушку еще до того, как она родит мою мать? В таком случае она не родит мою мать, а мать — меня, и тогда меня не будет, я не смогу отправиться в будущее и убить мою будущую бабушку. Это, в свою очередь, означает, что она без проблем родит мою мать, а мать — меня. Парадокс. Традиционное решение парадокса бабушки таково: путешественники во времени не могут изменить прошлое. Они всегда — часть прошлого. Да, вы могли отправиться в прошлое и выпить в компании бабушки чаю с печеньем, когда она была еще юной девушкой, но не могли убить ее, поскольку она должна родить вашу мать, которая родит вас. Решение должно быть самосогласованным. Кип Торн, Игорь Новиков и их коллеги сформулировали ряд мысленных экспериментов из области путешествий во времени, сталкивая бильярдные шары; они пытались показать, что всегда можно найти самосогласованные решения, не содержащие парадоксов.


Не беспокойтесь по поводу изменения истории: как бы вы ни старались, ничего у вас не выйдет. Если вернуться на «Титаник» и преду­предить капитана об айсберге, то капитан проигнорирует ваши слова, точно как он не придал значения всем остальным сообщениям об айсбергах, — ведь мы знаем, что корабль затонет. Вы убедитесь, что изменить ход событий невозможно. Хронопутешествия в фильме «Невероятные приключения Билла и Теда» построены по тому же принципу самосогласованности.

Альтернативный вариант решения парадокса бабушки — это эвереттовская многомировая теория квантовой механики. Мнения физиков по поводу этой теории разнятся, но давайте для начала разберемся, как она устроена. В многомировой теории считается, что множество параллельных миров могут сосуществовать, как железнодорожные пути в маневровом парке. Мы видим одну историю, словно наш поезд идет по конкретному пути. События, которые мы наблюдаем, подобны станциям, сменяющим друг друга. Вот Вторая мировая война… вот люди высаживаются на Луне и так далее. Но существует множество параллельных миров. Есть мир, где Вторая мировая война не произошла. Такая теория основана на подходе к квантовой механике как к сумме множества историй, предложенном Ричардом Фейнманом. Фейнман понял, что для расчета вероятности любого исхода того или иного будущего эксперимента нужно учесть все возможные истории, которые могли бы к нему привести. Кому-то кажется, что это просто очередное странное правило расчетов в квантовой механике, но сторонники многомировой модели считают, что все эти истории реальны и взаимодействуют друг с другом. Дэвид Дойч считает, что путешественник во времени может отправиться в прошлое и убить там свою бабушку, когда она была еще юной девушкой. В таком случае возникнет новое ответвление истории: в этом варианте истории будут и живой хронопутешественник, и его мертвая бабушка. Тот путь, где хронопутешественник все-таки родился и его бабушка осталась жива, также продолжает существовать. Путешественник по-прежнему помнит часть своей биографии, свершившейся до поворота на новый путь. Оба пути существуют.

Теперь у нас есть два адекватных решения парадокса бабушки. Первое — консервативное, где пространство-время представлено в виде единой самосогласованной четырехмерной скульптуры, неизменной по сути. Второе — более радикальная многомировая интерпретация квантовой механики. Оба решения работают.

Далее, если вернуться к мировой линии путешественника во времени, которая закольцовывается сама на себя в прошлом, то можно заметить в ней один изъян. Свет на этой схеме летит под углом 45°. Когда хронопутешественник переваливает через вершину, чтобы начать возвращение в прошлое, в какой-то точке уклон его мировой линии относительно оси времени должен быть больше 45°. Это означает, что в какой-то момент он должен превысить скорость света. На самом деле, переваливая через вершину схемы, он движется с бесконечной скоростью. Феномен взаимосвязи полетов со сверхсветовыми скоростями и путешествий во времени схвачен в следующем лимерике А.Г. Р. Баллера:

Очень шустрая мисс из Дакоты
Говорила: «Эйнштейн — это что-то!
Раз летала я где-то
Выше скорости света
И вернулась за день до отлета!»

Проблема в том, что (как продемонстрировал Эйнштейн в своей специальной теории относительности) невозможно сконструировать ракету, которая развивала бы сверхсветовую скорость. Если ваша скорость не превышает скорости, света, то ваша мировая линия никогда не расположится под углом более 45° относительно оси времени, и вернуться в прошлое не получится. Однако в общей теории относительности Эйнштейна, где пространство-время считается искривленным, можно обогнать луч света, срезав путь, если двинуться либо через кротовую нору, либо (что будет рассмотрено ниже) по космической струне. Если обогнать луч света, то, подобно нашей шустрой мисс, можно улететь в прошлое.

Допустим, у нас есть лист бумаги, на котором одно пространственное измерение откладывается по горизонтали, а время — по вертикали (рис. 21.3). В таком случае ваша мировая линия — это зеленая полоска на данном рисунке. Вы ленивы и просто сидите дома, поэтому ваша мировая линия идет ровно от нижнего до верхнего края листа. Однако в искривленном пространстве-времени действуют иные правила. Давайте свернем лист в цилиндр по горизонтали, склеив сверху лист скотчем. Теперь ваша мировая линия — это круг, уходящий в прошлое.

Вы все время движетесь вперед в будущее, но на самом деле заворачиваете в прошлое. То же самое произошло с экспедицией Магеллана: моряки все время плыли на запад, обогнули всю Землю и вернулись обратно в Европу. Этого бы ни в коем случае не произошло, если бы поверхность Земли была плоской. Аналогично, хронопутешественник все время движется в будущее, но, если пространство достаточно искривлено, он может вернуться к событиям, свершившимся у него в прошлом.

» Более подробно с книгой можно ознакомиться на сайте издательства
» Оглавление
» Отрывок

Для читателей данного блога скидка 20% по купону — Тайсон