В последней статье я уже упоминал о существовании альтернативных способов вычисления логических функций. В этой статье начну знакомить с вычислением логических функций непосредственно по событийному описанию (например STG). Тут не надо путать событийные описания с описаниями через состояния (пример — диаграмма изменений). Сам метод родился для синтеза асинхронных схем, но при желании его можно использовать и при синтезе синхронных схем. Отличительными чертами метода являются: 1) полный отказ от использования такого понятия как состояние (при объяснении я конечно буду ссылаться на это понятие); 2) существенное сокращение вычислений за счет использования информации о соседних состояниях. При машинных вычислениях это позволяет существенно сократить время вычислений и радикально решить проблему нехватки памяти при взрыве состояний. При ручных вычислениях метод позволяет при достаточной сноровке оперировать поведениями с сотнями сигналов. Речь конечно же идет о вычислении минимальных функций.
Для начала рассмотрим самые простые поведения: последовательные, циклические, каждый сигнал переключается ровно по 2 раза за цикл. Поведение будем представлять в виде строки, направление слева на право. Многоточие обозначает, что в этом месте возможна последовательность переключений каких-то сигналов.
Начнем с того, как на графе выглядит состояние.

Состояние это точка (красная) между двумя событиями. В данном случае это: a=0, b=1, c=0, d=1. В языке STG состояние это набор маркированных плэйсов.
Теперь посмотрим как на графе выглядит простая импликанта. Будем рассматривать конъюнкцию (функция И).
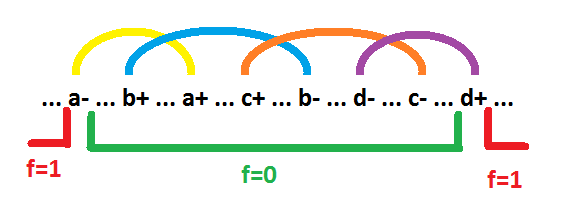
Зеленым подчеркнута зона где импликанта равна 0. Красным подчеркнута зона где импликанта равна 1. В этой зоне все сигналы, определяющие импликанту постоянны. Все пространство вне этой зоны представляет собой цепочку перехватов. Звенья этой цепочки (показаны сверху над графом) образованы переключениями сигналов, образующих импликанту. Каждое звено это пара переключений одного сигнала. Сигнал, образующий звено, на состояниях внутри этого звена поддерживает значение импликанты равным 0. Зона единиц (а соответственно и зона нулей) может быть прерывистой. Но пока такую возможность рассматривать нет необходимости. При принятых условиях такая структура цепочки перехватов для простых импликант является единственно возможной. Например, если бы событие c+ располагалось бы левее события a+, тогда сигнал b можно было бы из импликанты удалить. В дальнейшем под импликантой будем подразумевать зону единиц данной импликанты. Крайние события цепочки перехватов будем называть границами импликанты. На рисунке событие d+ — левая граница, событие a- — правая граница. Осталось выяснить какие сигналы входят в импликанту с инверсией, а какие без инверсии. Если звено начинается с "-" события, то сигнал входит в импликанту без инверсии (на рисунке сигналы a и d). Если звено начинается с "+" события, то сигнал входит в импликанту с инверсией (на рисунке сигналы b и c). В итоге, на рисунке изображено поведение импликанты a*!b*!c*d.
Теперь перейдем к построению импликанты. Для начала ответим на вопрос: что является основной характеристикой импликанты с точки зрения вычисления логических функций? Казалось бы это переменные (сигналы), которые эту импликанту составляют. Но на самом деле основной характеристикой импликанты является ее месторасположение на графе поведения (как мы условились расположение зоны единиц). А сигналы, составляющие импликанту, являются средством для достижения нужного расположения. То есть процесс построения импликанты это вычисление нужных сигналов с целью расположения импликанты в нужном месте на графе. Теперь встает вопрос: как задать место будущего расположения импликанты? Место расположения импликанты будем задавать 3 точками (состояниями).

Точка 2 это состояние, на котором импликанта обязательно должна принимать значение 1. Точки 1 и 3 это крайние состояния, на которых импликанта может принимать значение 1. То есть импликанта обязательно должна содержать точку 2 и может быть расширена вплоть до точек 1 и 3. Положение левой границы безразлично, правая граница должна быть максимально отодвинута от точки 2. Точки 1 и 3 могут совпадать с точкой 2 (по отдельности, но не вдвоем сразу).
Процесс построения импликанты это последовательный поиск сигналов — звеньев цепочки перехватов. Процесс этот удобнее вести справа налево (причины этого будут объяснены позже). Поиск начинается между точками 1 и 2. И заканчивается когда звено попадет между точками 2 и 3. Невозможность построения такой цепочки перехватов означает только одно: поведение содержит CSC конфликт. Так как мы ищем импликанты для минимальной функции, имеют значение два фактора, которые могут приходить в противоречие друг с другом: количество переменных в импликанте (то есть звеньев) и длина импликанты (множество состояний, которые она покрывает). Поэтому звенья выбираются самые длинные. Кроме последнего, которое выбирается по возможности покороче. Также надо учитывать момент, что последнее звено может быть заменено цепочкой более коротких звеньев. При этом длина самой импликанты может увеличиться.
Теперь опишу алгоритм вычисления простой импликанты, покрывающей точку 2. В качестве памяти алгоритм использует 2 множества: множество кандидатов на место текущего звена (множество P) и множество кандидатов на место следующего звена (множество N). Максимальное количество членов этих множеств равно количеству сигналов. Изначально множества пустые.
Шаг 1. Берем в рассмотрение событие, расположенное левее точки 2.
Шаг 2. Если рассматриваемое событие расположено левее точки 1, то а) сигнал, соответствующий рассматриваемому событию, добавляем в множество P, б) переходим к рассмотрению предшествующего события.
Шаг 3. Если рассматриваемое событие расположено справа от точки 3, то переходим к шагу 15.
Шаг 4. Если рассматриваемое событие расположено слева от точки 1, то а) если сигнал, соответствующий рассматриваемому событию, принадлежит множеству N, то исключаем этот сигнал из этого множества, в противном случае добавляем этот сигнал к этому множеству; б) если множество N пустое (это означает CSC конфликт), то выходим из алгоритма; в) множество P делаем равным множеству N, г) множество N делаем пустым, д) переходим к рассмотрению предшествующего события, е) переходим к шагу 3.
Шаг 5. Если сигнал, соответствующий рассматриваемому событию, принадлежит множеству N, то а) исключаем этот сигнал из этого множества, б) переходим к рассмотрению предшествующего события, в) переходим к шагу 3.
Шаг 6. Если сигнал, соответствующий рассматриваемому событию, не принадлежит множеству P, то а) добавляем этот сигнал в множество N, б) переходим к рассмотрению предшествующего события, в) переходим к шагу 3.
Шаг 7. Удаляем сигнал, соответствующий рассматриваемому событию, из множества P.
Шаг 8. Если множество P не пустое, то а) переходим к рассмотрению предшествующего события, б) переходим к шагу 3.
Шаг 9. Сигнал, соответствующий рассматриваемому событию, добавляем в импликанту в качестве переменной.
Шаг 10. Если множество N пустое (CSC конфликт), то выходим из алгоритма.
Шаг 11. Множество P делаем равным множеству N.
Шаг 12. Множество N делаем пустым.
Шаг 13. Переходим к рассмотрению предшествующего события.
Шаг 14. Переходим к шагу 3.
Шаг 15. Если сигнал, соответствующий рассматриваемому событию, не принадлежит множеству P, то а) переходим к рассмотрению предшествующего события, б) повторяем шаг 15.
Шаг 16. Сигнал, соответствующий рассматриваемому событию, добавляем в импликанту в качестве переменной.
Шаг 17. Импликанта построена. Завершение работы алгоритма.
Как видно сложность алгоритма вычисления простой импликанты по графу событий (при принятых условиях) пропорциональна количеству событий графа. Алгоритм также практически не требует затрат памяти.
Этот алгоритм настроен на вычисление импликанты с наименьшим количеством переменных. Чтобы получить импликанты с большим количеством переменных, но покрывающих больше состояний, необходимо небольшое усовершенствование. Необходимо запоминать последний удаленный из множества P сигнал. А также все сигналы удаленные из множества N после этого. После того как алгоритм подойдет к шагу 15 надо восстановить в множестве N удаленные и запомненные сигналы, последний удаленный из множества P сигнал добавить в импликанту и продолжить рассмотрение с события, после которого был удален сигнал из множества P в последний раз. Таким образом могут быть найдены все экстремали. Продолжение следует.
Для начала рассмотрим самые простые поведения: последовательные, циклические, каждый сигнал переключается ровно по 2 раза за цикл. Поведение будем представлять в виде строки, направление слева на право. Многоточие обозначает, что в этом месте возможна последовательность переключений каких-то сигналов.
Начнем с того, как на графе выглядит состояние.

Состояние это точка (красная) между двумя событиями. В данном случае это: a=0, b=1, c=0, d=1. В языке STG состояние это набор маркированных плэйсов.
Теперь посмотрим как на графе выглядит простая импликанта. Будем рассматривать конъюнкцию (функция И).
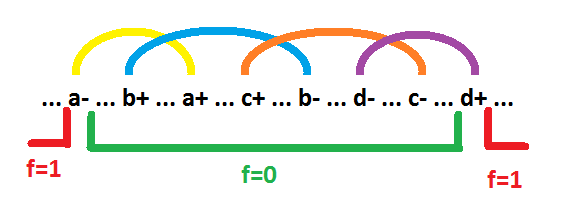
Зеленым подчеркнута зона где импликанта равна 0. Красным подчеркнута зона где импликанта равна 1. В этой зоне все сигналы, определяющие импликанту постоянны. Все пространство вне этой зоны представляет собой цепочку перехватов. Звенья этой цепочки (показаны сверху над графом) образованы переключениями сигналов, образующих импликанту. Каждое звено это пара переключений одного сигнала. Сигнал, образующий звено, на состояниях внутри этого звена поддерживает значение импликанты равным 0. Зона единиц (а соответственно и зона нулей) может быть прерывистой. Но пока такую возможность рассматривать нет необходимости. При принятых условиях такая структура цепочки перехватов для простых импликант является единственно возможной. Например, если бы событие c+ располагалось бы левее события a+, тогда сигнал b можно было бы из импликанты удалить. В дальнейшем под импликантой будем подразумевать зону единиц данной импликанты. Крайние события цепочки перехватов будем называть границами импликанты. На рисунке событие d+ — левая граница, событие a- — правая граница. Осталось выяснить какие сигналы входят в импликанту с инверсией, а какие без инверсии. Если звено начинается с "-" события, то сигнал входит в импликанту без инверсии (на рисунке сигналы a и d). Если звено начинается с "+" события, то сигнал входит в импликанту с инверсией (на рисунке сигналы b и c). В итоге, на рисунке изображено поведение импликанты a*!b*!c*d.
Теперь перейдем к построению импликанты. Для начала ответим на вопрос: что является основной характеристикой импликанты с точки зрения вычисления логических функций? Казалось бы это переменные (сигналы), которые эту импликанту составляют. Но на самом деле основной характеристикой импликанты является ее месторасположение на графе поведения (как мы условились расположение зоны единиц). А сигналы, составляющие импликанту, являются средством для достижения нужного расположения. То есть процесс построения импликанты это вычисление нужных сигналов с целью расположения импликанты в нужном месте на графе. Теперь встает вопрос: как задать место будущего расположения импликанты? Место расположения импликанты будем задавать 3 точками (состояниями).

Точка 2 это состояние, на котором импликанта обязательно должна принимать значение 1. Точки 1 и 3 это крайние состояния, на которых импликанта может принимать значение 1. То есть импликанта обязательно должна содержать точку 2 и может быть расширена вплоть до точек 1 и 3. Положение левой границы безразлично, правая граница должна быть максимально отодвинута от точки 2. Точки 1 и 3 могут совпадать с точкой 2 (по отдельности, но не вдвоем сразу).
Процесс построения импликанты это последовательный поиск сигналов — звеньев цепочки перехватов. Процесс этот удобнее вести справа налево (причины этого будут объяснены позже). Поиск начинается между точками 1 и 2. И заканчивается когда звено попадет между точками 2 и 3. Невозможность построения такой цепочки перехватов означает только одно: поведение содержит CSC конфликт. Так как мы ищем импликанты для минимальной функции, имеют значение два фактора, которые могут приходить в противоречие друг с другом: количество переменных в импликанте (то есть звеньев) и длина импликанты (множество состояний, которые она покрывает). Поэтому звенья выбираются самые длинные. Кроме последнего, которое выбирается по возможности покороче. Также надо учитывать момент, что последнее звено может быть заменено цепочкой более коротких звеньев. При этом длина самой импликанты может увеличиться.
Теперь опишу алгоритм вычисления простой импликанты, покрывающей точку 2. В качестве памяти алгоритм использует 2 множества: множество кандидатов на место текущего звена (множество P) и множество кандидатов на место следующего звена (множество N). Максимальное количество членов этих множеств равно количеству сигналов. Изначально множества пустые.
Шаг 1. Берем в рассмотрение событие, расположенное левее точки 2.
Шаг 2. Если рассматриваемое событие расположено левее точки 1, то а) сигнал, соответствующий рассматриваемому событию, добавляем в множество P, б) переходим к рассмотрению предшествующего события.
Шаг 3. Если рассматриваемое событие расположено справа от точки 3, то переходим к шагу 15.
Шаг 4. Если рассматриваемое событие расположено слева от точки 1, то а) если сигнал, соответствующий рассматриваемому событию, принадлежит множеству N, то исключаем этот сигнал из этого множества, в противном случае добавляем этот сигнал к этому множеству; б) если множество N пустое (это означает CSC конфликт), то выходим из алгоритма; в) множество P делаем равным множеству N, г) множество N делаем пустым, д) переходим к рассмотрению предшествующего события, е) переходим к шагу 3.
Шаг 5. Если сигнал, соответствующий рассматриваемому событию, принадлежит множеству N, то а) исключаем этот сигнал из этого множества, б) переходим к рассмотрению предшествующего события, в) переходим к шагу 3.
Шаг 6. Если сигнал, соответствующий рассматриваемому событию, не принадлежит множеству P, то а) добавляем этот сигнал в множество N, б) переходим к рассмотрению предшествующего события, в) переходим к шагу 3.
Шаг 7. Удаляем сигнал, соответствующий рассматриваемому событию, из множества P.
Шаг 8. Если множество P не пустое, то а) переходим к рассмотрению предшествующего события, б) переходим к шагу 3.
Шаг 9. Сигнал, соответствующий рассматриваемому событию, добавляем в импликанту в качестве переменной.
Шаг 10. Если множество N пустое (CSC конфликт), то выходим из алгоритма.
Шаг 11. Множество P делаем равным множеству N.
Шаг 12. Множество N делаем пустым.
Шаг 13. Переходим к рассмотрению предшествующего события.
Шаг 14. Переходим к шагу 3.
Шаг 15. Если сигнал, соответствующий рассматриваемому событию, не принадлежит множеству P, то а) переходим к рассмотрению предшествующего события, б) повторяем шаг 15.
Шаг 16. Сигнал, соответствующий рассматриваемому событию, добавляем в импликанту в качестве переменной.
Шаг 17. Импликанта построена. Завершение работы алгоритма.
Как видно сложность алгоритма вычисления простой импликанты по графу событий (при принятых условиях) пропорциональна количеству событий графа. Алгоритм также практически не требует затрат памяти.
Этот алгоритм настроен на вычисление импликанты с наименьшим количеством переменных. Чтобы получить импликанты с большим количеством переменных, но покрывающих больше состояний, необходимо небольшое усовершенствование. Необходимо запоминать последний удаленный из множества P сигнал. А также все сигналы удаленные из множества N после этого. После того как алгоритм подойдет к шагу 15 надо восстановить в множестве N удаленные и запомненные сигналы, последний удаленный из множества P сигнал добавить в импликанту и продолжить рассмотрение с события, после которого был удален сигнал из множества P в последний раз. Таким образом могут быть найдены все экстремали. Продолжение следует.

